利用者:加藤勝憲/電気抵抗とコンダクタンス

Template:Electromagnetism $R={\frac {V}{I}},\qquad G={\frac {I}{V}}={\frac {1}{R}}$ $I\propto V$ 物体の電気抵抗は、電流の流れに対する抵抗の尺度です。その逆数はelectrical conductance、電流の流れやすさを測定します。電気抵抗は、機械的摩擦と概念的に類似しています。電気抵抗のSI単位はオーム( $Ω$ ) ですが、電気コンダクタンスはジーメンス(S) で測定されます (以前は「モー」と呼ばれ、 $℧$ で表されます)。

物体の抵抗は、その物体が作られている材料に大きく依存します。ゴムのような電気絶縁体でできた物体は、抵抗が非常に高く、伝導率が低い傾向がありますが、金属のような導電体でできた物体は、抵抗が非常に低く、伝導率が高い傾向があります。この関係は、抵抗率または導電率によって定量化されます。ただし、材料の性質だけが抵抗とコンダクタンスの要因ではありません。オブジェクトのサイズと形状にも依存します。これは、これらのプロパティが集中的ではなく広範であるためです。たとえば、ワイヤの抵抗は、長くて細い場合は高く、短くて太い場合は低くなります。抵抗がゼロの超伝導体を除いて、すべての物体は電流に抵抗します。

物体の抵抗 $R$ は、物体にかかる電圧 $V$ と物体を流れる電流 $I$ の比として定義されますが、コンダクタンス $G$ は逆数です。 ${\begin{aligned}R&=\rho {\frac {\ell }{A}},\\[5pt]G&=\sigma {\frac {A}{\ell }}\,.\end{aligned}}$ さまざまな材料と条件に対して、 $V$ と $I$ は互いに正比例するため、 $R$ と $G$ は定数です (ただし、オブジェクトのサイズと形状、材料、およびその他の要因によって異なります)。温度や歪みなど）。この比例関係をオームの法則と呼び、それを満たす材料をオーミック材料と呼びます。

トランス、ダイオード、バッテリーなどの他のケースでは、 $V$ と $I$ は正比例しません。比率

序章

analogy of resistance — The hydraulic analogy compares electric current flowing through circuits to water flowing through pipes. When a pipe (left) is filled with hair (right), it takes a larger pressure to achieve the same flow of water. Pushing electric current through a large resistance is like pushing water through a pipe clogged with hair: It requires a larger push (electromotive force) to drive the same flow (electric current).

油圧の例えでは、ワイヤ (または抵抗器) を流れる電流は、パイプを流れる水に似ており、ワイヤ全体の電圧降下は、パイプを通して水を押し出す圧力降下に似ています。コンダクタンスは、特定の圧力に対して発生する流量に比例し、抵抗は、特定の流量を達成するために必要な圧力に比例します。

電圧自体ではなく、電圧降下(つまり、抵抗の一方の側と他方の側の電圧の差) が、抵抗に電流を押し込む駆動力を提供します。水力学でも同様です。圧力自体ではなく、パイプの両側の圧力差がパイプを通る流れを決定します。たとえば、パイプの上に大きな水圧があり、パイプを通って水を押し下げようとすることがあります。しかし、パイプの下には同様に大きな水圧があり、パイプを通って水を押し上げようとします。これらの圧力が等しい場合、水は流れません。 (右の画像では、パイプの下の水圧はゼロです。 )

ワイヤ、抵抗器、またはその他の要素の抵抗とコンダクタンスは、主に次の 2 つの特性によって決まります。

ジオメトリ (形状)、および
素材

長くて狭いパイプは、幅が広くて短いパイプよりも水を押し出すのが難しいため、形状は重要です。同様に、長くて細い銅線は、短くて太い銅線よりも抵抗が高くなります (コンダクタンスが低くなります)。

素材も重要です。髪の毛で満たされたパイプは、同じ形とサイズのきれいなパイプよりも水の流れを制限します。同様に、電子は銅線を自由かつ容易に流れることができますが、同じ形状とサイズの鋼線を容易に流れることはできず、ゴムのような絶縁体はその形状に関係なく本質的にまったく流れません。銅、鋼、ゴムの違いは、それらの微視的構造と電子配置に関連しており、抵抗率と呼ばれる特性によって定量化されます。

形状と材料に加えて、温度など、抵抗とコンダクタンスに影響を与えるさまざまな要因があります。以下を参照してください。

導体と抵抗器

A 75 Ω resistor, as identified by its electronic color code (violet–green–black–gold–red). An ohmmeter could be used to verify this value.

電気が流れる物質を導体と呼びます。回路で使用するための特定の抵抗値を持つ導電性材料を抵抗器と呼びます。導体は、金属、特に銅やアルミニウムなどの導電率の高い材料でできています。一方、抵抗器は、必要な抵抗値、消費するエネルギー量、精度、コストなどの要因に応じて、さまざまな材料で作られています。

オームの法則

The current–voltage characteristics of four devices: Two resistors, a diode, and a battery. The horizontal axis is voltage drop, the vertical axis is current. Ohm's law is satisfied when the graph is a straight line through the origin. Therefore, the two resistors are *ohmic*, but the diode and battery are not.

多くの材料では、材料を流れる電流 $I$ は、材料に印加される電圧 $V$ に比例します。Template:Glossary start Template:Term Template:Ghat Template:Defn Template:Term Template:Ghat Template:Defn Template:Glossary end $I\propto V$

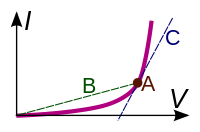
幅広い電圧と電流に対応。したがって、これらの材料で作られた物体または電子部品の抵抗とコンダクタンスは一定です。この関係をオームの法則と呼び、これに従う材料をオーミック材料と呼びます。オーミックコンポーネントの例としては、ワイヤと抵抗器があります。オームデバイスの電流 - 電圧グラフは、正の傾きを持つ原点を通る直線で構成されます。

電子機器で使用されるその他のコンポーネントや材料は、オームの法則に従いません。電流は電圧に比例しないため、抵抗は電圧と電流に応じて変化します。これらは非線形または非オーミックと呼ばれます。例としては、ダイオードや蛍光灯があります。非オーミックデバイスの電流-電圧曲線は曲線です。

抵抗率と導電率の関係

特定の物体の抵抗は、主に 2 つの要因に依存します。それは、その物体がどのような材料でできているか、およびその形状です。特定の材料の場合、抵抗は断面積に反比例します。たとえば、太い銅線は、他の点では同じである細い銅線よりも抵抗が低くなります。また、特定の材料の場合、抵抗は長さに比例します。たとえば、長い銅線は、他の点では同じである短い銅線よりも抵抗が高くなります。したがって、断面が均一な導体の抵抗 $R$ とコンダクタンス $G$ は、次のように計算できます。 ${\begin{aligned}Z&=R+jX\\Y&=G+jB\end{aligned}}$ どこ $\ell$ はメートル(m) で測定された導体の長さ、 $A$ は平方メートル(m ² ) で測定された導体の断面積、 $σ$ ( sigma ) は 1 メートルあたりのジーメンスで測定された電気伝導率(S·m) ⁻¹ )、 $ρ$ ( rho ) は材料の電気抵抗率(比電気抵抗とも呼ばれます) で、オームメートル (Ω・m) で測定されます。抵抗率と導電率は比例定数であるため、ワイヤの形状ではなく、ワイヤの材質のみに依存します。抵抗率と導電率は逆数です : $\rho =1/\sigma$ .抵抗率は、電流に対抗する材料の能力の尺度です。

この式は、電流密度が導体内で完全に均一であると仮定しているため、正確ではありませんが、実際の状況では常にそうであるとは限りません。ただし、この式は、ワイヤなどの細長い導体の適切な近似値を提供します。

この公式が正確でないもう 1 つの状況は、交流(AC) の場合です。これは、表皮効果により、導体の中心付近で電流の流れが阻害されるためです。このため、幾何学的断面積と実際に電流が流れる有効断面積が異なるため、抵抗が予想以上に高くなります。同様に、互いに近くにある 2 つの導体に AC 電流が流れると、近接効果により抵抗が増加します。商用電源周波数では、これらの影響は、変電所のバスバー^[1]や数百アンペアを超える大規模な電力ケーブルなど、大電流を運ぶ大規模な導体にとって重要です。

さまざまな材料の抵抗率は、非常に大きく異なります。たとえば、テフロンの導電率は、銅の導電率の約 10 ³⁰分の 1 です。大まかに言えば、これは、金属が「非局在化」された電子を多数持っているためであり、それらはどの場所にも留まらないため、長い距離を自由に移動できます。テフロンなどの絶縁体では、各電子が 1 つの分子にしっかりと結合しているため、引き離すには大きな力が必要です。半導体は、これら 2 つの両極端の間にあります。詳細については、電気抵抗率と導電率の記事を参照してください。電解質溶液の場合は、次の記事を参照してください:導電率 (電解) .

抵抗率は温度によって変化します。半導体では、光にさらされると抵抗率も変化します。以下を参照してください。

計測

$P=I^{2}R$

抵抗を測定する器具はオーム計と呼ばれます。単純なオーム計は、測定リードの抵抗が測定を妨げる電圧降下を引き起こすため、低抵抗を正確に測定できません。そのため、より正確なデバイスは4 端子センシングを使用します。

代表値

選択したオブジェクトの典型的な抵抗値
成分	抵抗 (Ω)
1メートルの銅線1本 mm 径	0.02 ^{[注釈 1]}
1 km架空送電線(標準)	0.03 ^[3]
単三電池（典型的な内部抵抗）	0.1 ^{[注釈 2]}
白熱電球のフィラメント（代表的なもの）	200–1000 ^[a]
人体	1000–100,000 ^{[注釈 3]}

静的および微分抵抗

$R(T)=R_{0}[1+\alpha (T-T_{0})]$

The current–voltage curve of a non-ohmic device (purple). The static resistance at point A is the inverse slope of line B through the origin. The differential resistance at A is the inverse slope of tangent line C.

The current–voltage curve of a component with negative differential resistance, an unusual phenomenon where the current–voltage curve is non-monotonic.

ダイオードやバッテリーなどの多くの電気要素は、オームの法則を満たしていnot。これらは非オーミックまたは非線形と呼ばれ、それらの電流 - 電圧曲線は原点を通る直線ではありnot。

抵抗とコンダクタンスは、非オーミック要素に対しても定義できます。ただし、オーミック抵抗とは異なり、非線形抵抗は一定ではなく、デバイスを流れる電圧または電流によって変化します。すなわち、その動作点。耐性には^[6] ^[7]の 2 種類があります。 Template:Glossary start Template:Term Template:Ghat Template:Defn Template:Term Template:Ghat Template:Defn Template:Glossary end

ポータル Electronics

交流回路

インピーダンスとアドミタンス

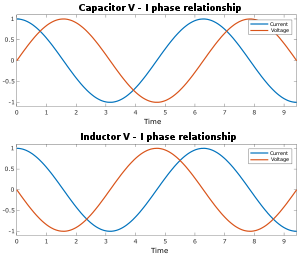
交流電流が回路を流れるとき、回路要素の電流と電圧の関係は、大きさの比だけでなく、位相の差によっても特徴付けられます。たとえば、理想的な抵抗器では、電圧が最大に達する瞬間に、電流も最大に達します (電流と電圧は同相で振動しています)。ただし、コンデンサまたはインダクタの場合、電圧がゼロを通過するときに最大電流が流れ、その逆も同様です (電流と電圧は位相が 90° ずれて振動しています。下の画像を参照してください)。複素数は、電流と電圧の位相と大きさの両方を追跡するために使用されます。 ${\begin{array}{cl}u(t)&=\operatorname {\mathcal {R_{e}}} \left(U_{0}\cdot e^{j\omega t}\right)\\i(t)&=\operatorname {\mathcal {R_{e}}} \left(I_{0}\cdot e^{j(\omega t+\varphi )}\right)\\Z&={\frac {U}{\ I\ }}\\Y&={\frac {\ 1\ }{Z}}={\frac {\ I\ }{U}}\end{array}}$ どこ：

$t$ is time;
$u (t)$ and $i (t)$ are the voltage and current as a function of time, respectively;
$U 0$ and $I 0$ indicate the amplitude of the voltage and current, respectively;
$\omega$ is the angular frequency of the AC current;
$\varphi$ is the displacement angle;
$U$ and $I$ are the complex-valued voltage and current, respectively;
$Z$ and $Y$ are the complex impedance and admittance, respectively;
${\mathfrak {Re}}$ indicates the real part of a complex number; and
$j={\sqrt {-1}}$ is the imaginary unit.

インピーダンスとアドミタンスは、実数部と虚数部に分解できる複素数として表すことができます。 ${\begin{aligned}Z&=R+jX\\Y&=G+jB~.\end{aligned}}$ ここで、 $R$ は抵抗、 $G$ はコンダクタンス、 $X$ はリアクタンス、 $B$ はサセプタンスです。理想的な抵抗の場合、 $Z$ と $Y$ はそれぞれ $R$ と $G$ に減少します。しかし、コンデンサとインダクタを含む AC ネットワークの場合、 $X$ と $B$ はゼロではありません。 ${\begin{aligned}R&={\frac {G}{\ G^{2}+B^{2}\ }}\ ,\qquad &X={\frac {-B~}{\ G^{2}+B^{2}\ }}\ ,\\G&={\frac {R}{\ R^{2}+X^{2}\ }}\ ,\qquad &B={\frac {-X~}{\ R^{2}+X^{2}\ }}\ ,\end{aligned}}$ which are true in all cases, whereas $\ R=1/G\$ is only true in the special cases of either DC or reactance-free current.

The complex angle $\ \theta =\arg(Z)=-\arg(Y)\$ is the phase difference between the voltage and current passing through a component with impedance $Z$ . For capacitors and inductors, this angle is exactly -90° or +90°, respectively, and $X$ and $B$ are nonzero. Ideal resistors have an angle of 0°, since $X$ is zero (and hence $B$ also), and $Z$ and $Y$ reduce to $R$ and $G$ respectively. In general, AC systems are designed to keep the phase angle close to 0° as much as possible, since it reduces the reactive power, which does no useful work at a load. In a simple case with an inductive load (causing the phase to increase), a capacitor may be added for compensation at one frequency, since the capacitor's phase shift is negative, bringing the total impedance phase closer to 0° again.

$Y$ is the reciprocal of $Z$ ( $\ Z=1/Y\$ ) for all circuits, just as $R=1/G$ for DC circuits containing only resistors, or AC circuits for which either the reactance or susceptance happens to be zero ( $X$ or $B = 0$ , respectively) (if one is zero, then for realistic systems both must be zero).

周波数依存性

AC 回路の重要な特徴は、抵抗とコンダクタンスが周波数に依存する可能性があることです。これは、普遍的な誘電応答として知られる現象です。 ^[8]上記の理由の 1 つは、表皮効果(および関連する近接効果) です。もう1つの理由は、抵抗率自体が周波数に依存する可能性があることです（ Drudeモデル、深い準位トラップ、共鳴周波数、 Kramers-Kronig関係などを参照）。 )

エネルギー散逸とジュール熱

Running current through a material with resistance creates heat, in a phenomenon called Joule heating. In this picture, a cartridge heater, warmed by Joule heating, is glowing red hot.

抵抗器 (および抵抗を持つその他の要素) は、電流の流れに対抗します。したがって、電流を抵抗に通すには電気エネルギーが必要です。この電気エネルギーは消費され、その過程で抵抗器が加熱されます。これは、ジュール加熱( James Prescott Jouleにちなんで) と呼ばれ、オーム加熱または抵抗加熱とも呼ばれます。

電気エネルギーの散逸は望ましくないことが多く、特に電力線の伝送損失の場合に顕著です。高電圧伝送は、特定の電力の電流を減らすことによって損失を減らすのに役立ちます。

一方、ジュール加熱は、電気ストーブやその他の電気ヒーター(抵抗ヒーターとも呼ばれます) などで役立つ場合があります。別の例として、白熱灯はジュール加熱に依存しています。フィラメントは、熱放射(白熱とも呼ばれます) で「白熱」するほどの高温に加熱されます。

ジュール熱の式は次のとおりです。

ここで、 $P$ は電気エネルギーから熱エネルギーに変換された電力(単位時間あたりのエネルギー)、 $R$ は抵抗、 $I$ は抵抗を流れる電流です。

その他条件依存

温度依存性

室温付近では、金属の抵抗率は通常、温度が上昇するにつれて増加しますが、半導体の抵抗率は通常、温度が上昇するにつれて減少します。絶縁体と電解質の抵抗率は、システムによって増減する場合があります。詳細な動作と説明については、電気抵抗率と導電率を参照してください。

その結果、ワイヤ、抵抗器、およびその他のコンポーネントの抵抗は、温度によって変化することがよくあります。この影響は望ましくない場合があり、極端な温度では電子回路が誤動作する可能性があります。ただし、場合によっては、その効果が有効に活用されます。コンポーネントの温度依存抵抗が意図的に使用される場合、そのコンポーネントは測温抵抗体またはサーミスタと呼ばれます。 (測温抵抗体は金属、通常はプラチナでできていますが、サーミスタはセラミックまたはポリマーでできています。 )

測温抵抗体とサーミスタは、一般的に 2 つの方法で使用されます。まず、温度計として使用できます。抵抗を測定することで、環境の温度を推測できます。第 2 に、ジュール熱(自己発熱とも呼ばれます) と組み合わせて使用できます。抵抗器に大きな電流が流れると、抵抗器の温度が上昇し、抵抗値が変化します。したがって、これらのコンポーネントは、ヒューズと同様の回路保護の役割、回路内のフィードバック、または他の多くの目的で使用できます。一般に、自己発熱により、抵抗器が非線形でヒステリシスのある回路要素に変化する可能性があります。詳細については、サーミスタ#自己発熱効果を参照してください。

温度 $T$ があまり変化しない場合、通常は線形近似が使用されます。

どこ $\alpha$ は抵抗温度係数と呼ばれ、 $T_{0}$ は固定基準温度 (通常は室温) であり、 $R_{0}$ 温度での抵抗 $T_{0}$ .パラメータ $\alpha$ は、測定データからフィッティングされた経験的パラメーターです。直線近似はあくまで近似なので、 $\alpha$ 異なる基準温度では異なります。このため、温度を指定するのが通常です。 $\alpha$ のように接尾辞を付けて測定されました。 $\alpha _{15}$ であり、この関係は基準付近の温度範囲でのみ保持されます。 ^[9]

温度係数 $\alpha$ 通常は+3×10⁻³ K−1 +6×10⁻³ K−1室温付近の金属の場合は+6×10⁻³ K−1 。通常、半導体と絶縁体では負であり、大きさは大きく異なります。 ^{[注釈 4]}

ひずみ依存性

導体の抵抗が温度に依存するように、導体の抵抗は歪みに依存します。 ^[10]導体を張力下 (導体の伸張という形で歪みをもたらす応力の形) に置くことにより、張力下にある導体のセクションの長さが増加し、その断面積が減少します。これらの効果は両方とも、導体の歪み部分の抵抗の増加に寄与します。圧縮（反対方向の歪み）下では、導体の歪み部分の抵抗が減少します。この効果を利用するために構築されたデバイスの詳細については、ひずみゲージに関する説明を参照してください。

光照度依存性

一部の抵抗器、特に半導体で作られた抵抗器は光伝導性を示します。これは、光が当たると抵抗が変化することを意味します。したがって、それらはフォトレジスター (または光依存抵抗器) と呼ばれます。これらは一般的なタイプの光検出器です。

超伝導

超伝導体は、 $V = 0$ および $I \neq 0$ を持つことができるため、抵抗が正確にゼロでコンダクタンスが無限大の物質です。これは、ジュール熱がないこと、つまり電気エネルギーの散逸がないことも意味します。そのため、超電導線を閉ループにすると、ループの周りに電流が永遠に流れます。超伝導体は4 K付近の温度まで冷却する必要があります4 Kニオブ-スズ合金のようなほとんどの金属超伝導体の液体ヘリウムによる4 K 、または77 K付近の温度への冷却77 K高価で脆くデリケートなセラミック高温超伝導体用の液体窒素による77 Kそれにもかかわらず、超電導磁石を含む超電導の多くの技術的応用があります。

参照

コンダクタンス量子
- フォンクリツィング定数(その逆数)
電気測定
接触抵抗
材料の伝導の物理的メカニズムに関する詳細については、電気抵抗率と伝導率を参照してください。
ジョンソン・ナイキスト・ノイズ
高精度抵抗測定のスタンダード、量子ホール効果。
抵抗器
RKMコード
直列回路と並列回路
シート抵抗
SI電磁気学ユニット
熱抵抗
分圧器
電圧降下

脚注

^ The resistivity of copper is about 1.7×10⁻⁸ Ω.m.^[2]
^ For a fresh Energizer E91 AA alkaline battery, the internal resistance varies from 0.9 Ω at −40 °C, to 0.1 Ω at +40 °C.^[4]
^ 100 kΩ for dry skin contact, 1 kΩ for wet or broken skin contact. High voltage breaks down the skin, lowering resistance to 500 Ω. Other factors and conditions are relevant as well. For more details, see the electric shock article, and NIOSH 98-131.^[5]
^ See Electrical resistivity and conductivity for a table. The temperature coefficient of resistivity is similar but not identical to the temperature coefficient of resistance. The small difference is due to thermal expansion changing the dimensions of the resistor.

参考文献

^ Fink; Beaty (1923). “Standard Handbook for Electrical Engineers”. Nature 111 (2788): 17–19. Bibcode: 1923Natur.111..458R. doi:10.1038/111458a0.
^ Cutnell, John D.; Johnson, Kenneth W. (1992). Physics (2nd ed.). New York: Wiley. p. 559. ISBN 978-0-471-52919-4
^ McDonald, John D. (2016). Electric Power Substations Engineering (2nd ed.). Boca Raton, Florida: CRC Press. pp. 363ff. ISBN 978-1-4200-0731-2
^ Battery internal resistance (PDF) (Report). Energizer Corp.
^ “Worker Deaths by Electrocution”. National Institute for Occupational Safety and Health. 2014年11月2日閲覧。
^ Brown, Forbes T. (2006). Engineering System Dynamics: A Unified Graph-Centered Approach (2nd ed.). Boca Raton, Florida: CRC Press. p. 43. ISBN 978-0-8493-9648-9
^ Kaiser, Kenneth L. (2004). Electromagnetic Compatibility Handbook. Boca Raton, Florida: CRC Press. pp. 13 – 52. ISBN 978-0-8493-2087-3
^ Zhai, Chongpu; Gan, Yixiang; Hanaor, Dorian; Proust, Gwénaëlle (2018). “Stress-dependent electrical transport and its universal scaling in granular materials”. Extreme Mechanics Letters 22: 83–88. arXiv:1712.05938. doi:10.1016/j.eml.2018.05.005.
^ Ward, M.R. (1971). Electrical Engineering Science. McGraw-Hill. pp. 36–40
^ Meyer, Sebastian (2022), “Characterization of the deformation state of magnesium by electrical resistance” (英語), Volume 215, Scripta Materialia, 215, pp. 114712, doi:10.1016/j.scriptamat.2022.114712

外部リンク

“Resistance calculator”. Clemson University. 2010年7月11日時点のオリジナルよりアーカイブ。2023年11月3日閲覧。
“Electron conductance models using maximal entropy random walks”. wolfram.com. 2023年11月3日閲覧。

[[Category:電気]] [[Category:未査読の翻訳があるページ]]
引用エラー: 「lower-alpha」という名前のグループの <ref> タグがありますが、対応する <references group="lower-alpha"/> タグが見つかりません

[3] The resistivity of copper is about 1.7×10⁻⁸ Ω.m.^[2]

[6] For a fresh Energizer E91 AA alkaline battery, the internal resistance varies from 0.9 Ω at −40 °C, to 0.1 Ω at +40 °C.^[4]

[9] 100 kΩ for dry skin contact, 1 kΩ for wet or broken skin contact. High voltage breaks down the skin, lowering resistance to 500 Ω. Other factors and conditions are relevant as well. For more details, see the electric shock article, and NIOSH 98-131.^[5]

[14] See Electrical resistivity and conductivity for a table. The temperature coefficient of resistivity is similar but not identical to the temperature coefficient of resistance. The small difference is due to thermal expansion changing the dimensions of the resistor.

[1] Fink; Beaty (1923). “Standard Handbook for Electrical Engineers”. Nature 111 (2788): 17–19. Bibcode: 1923Natur.111..458R. doi:10.1038/111458a0.

[Cutnell-2] Cutnell, John D.; Johnson, Kenneth W. (1992). Physics (2nd ed.). New York: Wiley. p. 559. ISBN 978-0-471-52919-4

[4] McDonald, John D. (2016). Electric Power Substations Engineering (2nd ed.). Boca Raton, Florida: CRC Press. pp. 363ff. ISBN 978-1-4200-0731-2

[5] Battery internal resistance (PDF) (Report). Energizer Corp.

[8] “Worker Deaths by Electrocution”. National Institute for Occupational Safety and Health. 2014年11月2日閲覧。

[brown-10] Brown, Forbes T. (2006). Engineering System Dynamics: A Unified Graph-Centered Approach (2nd ed.). Boca Raton, Florida: CRC Press. p. 43. ISBN 978-0-8493-9648-9

[kaiser-11] Kaiser, Kenneth L. (2004). Electromagnetic Compatibility Handbook. Boca Raton, Florida: CRC Press. pp. 13 – 52. ISBN 978-0-8493-2087-3

[12] Zhai, Chongpu; Gan, Yixiang; Hanaor, Dorian; Proust, Gwénaëlle (2018). “Stress-dependent electrical transport and its universal scaling in granular materials”. Extreme Mechanics Letters 22: 83–88. arXiv:1712.05938. doi:10.1016/j.eml.2018.05.005.

[13] Ward, M.R. (1971). Electrical Engineering Science. McGraw-Hill. pp. 36–40

[15] Meyer, Sebastian (2022), “Characterization of the deformation state of magnesium by electrical resistance” (英語), Volume 215, Scripta Materialia, 215, pp. 114712, doi:10.1016/j.scriptamat.2022.114712

[1]

[注釈 1]

[3]

[注釈 2]

[a]

[注釈 3]

[6]

[7]

[8]

[9]

[注釈 4]

[10]

[2]

[4]

[5]