傾き (数学)

平面上の直線の傾きは、垂直移動距離を水平移動距離で割った m = Δy/Δx で定義される

数学における平面上の直線の傾き（かたむき、英: slope）あるいは勾配（こうばい、英: gradient）は、その傾斜の具合を表す数値である。ただし、鉛直線に対する傾きは定義されない。一般的な用語として水平は傾いているとは言われないが、数学では「傾き０」とされ水平も傾きに含まれる。

傾きは普通、直線上の2点間の変化の度合い、すなわち x の変化量に対する y の変化量の比率として定義される。また、同値な定義として、傾き m は傾斜角を θ として

$m=\tan \theta$

と書くことができる。

曲線上の微分可能な1点に対しても、傾斜の具合を表す数値（微分係数）が、傾きの考え方により定義できる。

傾きの概念は、地理学および土木工学における斜度や勾配（たとえば道路など）に直接応用される。

定義

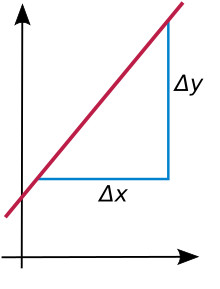
xy平面上の直線の傾きは、x座標の増加量に対する y座標の増加量の比率と定義される。式で書けば、直線の傾き m は

$m={\frac {\Delta y}{\Delta x}}$

で記述される。ここで、ギリシア文字 "Δ"（デルタ）は、数学において「増加量」や「増分」を表す符牒としてよく用いられる。

増加量とは差のことなので、直線上の2点を任意に取り、それらを (x₁, y₁), (x₂, y₂) とする。このとき、m は

$m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$

で求められる。

これらの等式から分かるように、鉛直線（y軸に平行な直線）の傾きは、ゼロ除算となり、定義されない。

（例）

直線が2点 $P(1,2)$, $Q(13,8)$ を通るとする。増加量として、P に対する Q の増加量と考えるか、Q に対する P の増加量と考えるかで符号の違いが現れるが、それらの商である傾きとしてはどちらも変わらない。ここでは P に対する Q の増加量を考える。

xの増加量 Δx = 13 − 1 = 12

yの増加量 Δy = 8 − 2 = 6

傾き m とは、y座標の増加量 Δx に対する y座標の増加量 Δy の比率のことなので、

$m={\frac {\Delta y}{\Delta x}}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}={\frac {8-2}{13-1}}={\frac {6}{12}}={\frac {1}{2}}$

である。

直線が2点 $P(4,15)$, $Q(3,21)$ を通るならば、傾きは

$m={\frac {21-15}{3-4}}={\frac {6}{-1}}=-6$

である。

傾斜角による記述

傾斜の度合いを表す傾きは、傾斜角と関係が深い。たとえば、傾き 1 の直線の傾斜角は 45° である。傾き −1 ならば、傾斜角を 0°～180° の範囲で考えると 135°、−90°～90° の範囲で考えると −45° である。なお、鉛直線の傾きは定義されなかったが、傾斜角は定義され、90° である。

傾斜角とは、直線と x軸の正の部分が作る角（反時計回りが正の向き）と定義される。取り得る範囲として 0° ≤ θ < 180° または −90° < θ ≤ 90° の2つの流儀がある（状況に応じて使い分ける）。

直線の傾きを m、傾斜角を θ とすると、2つの間には、三角法における正接函数を用いて

$m=\tan \theta \ (\iff \theta =\arctan m)$

の関係がある。

性質

• 異なる2直線が平行であるための必要十分条件は、それらの傾きが等しいこと、または、傾きがともに定義されないことである。
• 異なる2直線が直交するための必要十分条件は、傾きの積が −1、または、傾きが 0 と定義されない場合であることである。

たとえば、傾き ${\tfrac {2}{7}}$ の直線に垂直な直線の傾きは $-{\tfrac {7}{2}}$ である。

• 傾き m の直線と傾き m' の直線が作る角 θ は

$\tan \theta =\pm {\frac {m-m'}{1+mm'}}$

で求められる（三角関数の加法定理）。

1次関数における傾き

傾き・切片

y は x の一次関数であるとする。このとき、x と y には y = ax + b と表される関係があり、そのグラフは直線となる。この直線の傾きは a に等しい。

（証明）

y = ax + b のグラフ上の任意の2点 P, Q を取る。P, Q の x座標をそれぞれ x₁, x₂ とすると、P, Q の座標は

P (x₁, ax₁ + b), Q (x₂, ax₂ + b)

である。

xの増加量 Δx = x₂ − x₁

yの増加量 Δy = (ax₂ + b) − (ax₁ + b)

= ax₂ − ax₁

= a (x₂ − x₁)

傾き m は、

$m={\frac {\Delta y}{\Delta x}}={\frac {a(x_{2}-x_{1})}{x_{2}-x_{1}}}=a$（証明終）

1次関数 y = ax + b において、a を傾きと呼ぶのに対して、b を y切片と呼ぶ。1次関数の y切片は、グラフ（直線）が y 軸と交わる点の y 座標に等しい。したがって、y = ax + b の形の方程式を「傾き・切片標準形」と呼ぶこともある。

1次関数 y = ax + b のグラフは、y軸平行の直線にはなりえないことに注意が必要である。

1次関数の決定

1次関数の傾き m と直線上の1点 (x₁, y₁) が既知ならば、1次関数の方程式は

$y-y_{1}=m(x-x_{1})$

で与えられる（これを「点・傾き標準形」と呼ぶことがある）。

（例）

1次関数のグラフが2点 (2, 8), (3, 20) を通るとする。1次関数の傾き m は

${\frac {20-8}{3-2}}=12$

だから、直線の方程式は1点・傾き標準形で

y − 8 = 12(x − 2)

と求まる。これはつまり

y = 12x − 16

である。

直線の一般形

前述の通り、1次関数のグラフは全ての直線を表さない。2変数線型方程式の一般形

$ax+by+c=0$

は全ての直線を表す。b ≠ 0 ならば、傾きが存在し、$-{\tfrac {a}{b}}$ である。

直線の切片形

${\frac {x}{a}}+{\frac {y}{b}}=1$ の形の方程式は切片形と呼ばれる。このとき y は x の1次関数で、

x切片が a

y切片が b

となる。この直線の傾きは $-{\tfrac {b}{a}}$ である。

方向ベクトルとの関係

直線の傾きが m であることは、その直線の方向ベクトルが (1, m) であることと同値である。

微分係数

各点における微分係数とは、その点における曲線の接線の傾きのことである。各点に対して図の直線は常に曲線（青）の接線を表す。接線を、微分係数が正のときは緑、負のときは赤、0 のときは黒で表している。

曲線上の1点に対しても、そこで微分可能ならば、傾斜の具合を表す数値としての傾きが定義できる。

Δx と Δy を曲線上の2点間のそれぞれ x座標、y座標の増加量とすると、その2点を通る直線（弦という）の傾き m は

$m={\frac {\Delta y}{\Delta x}}$

である。この2点間を狭めたときの m の極限が、そこを直線として近似した傾きと考えられる。これは接線の傾きであり、微分係数と呼ばれる。場所 x を変数とした

${\frac {dy}{dx}}=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}$

を、曲線の導関数と呼ぶ。

微分係数が定義できない例としては、次のような例がある。

• 三角屋根型
  • y = |x| における x = 0
• 振動型
  • $y=\left\{{\begin{array}{ll}x\sin {\frac {1}{x}}&(x\neq 0)\\0&(x=0)\end{array}}\right.$（これは x = 0 で連続である）における x = 0
  • ワイエルシュトラス関数

関連項目

• 勾配 (ベクトル解析): 多変数への一般化
• 平面における直線の標準形
• 縦断勾配