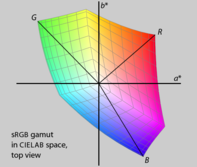
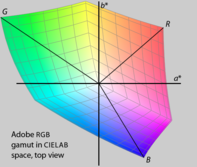
HSL色空間とHSV色空間

図1：HSL色空間（左列、aからd）とHSV色空間（右列、eからh）。最上段（a, e）はそれぞれの色空間を円柱で示した図であり、その他は各色空間の3つの成分のうち1つを固定して、残り2つを同時に示した2次元プロットである。 b, f は彩度（Saturation）一定の円柱側面（この図では円柱の最も外側）。c, g はHSLの輝度（Lightness）またはHSVの明度（Value）一定の断面（この図では円柱を2等分する水平の断面）。d, h は色相（Hue）一定の断面（この図では0度の赤とその補色である180度のシアンを結ぶ垂直の断面）。

HSL色空間（HLS色空間ともよばれる）とHSV色空間（HSB色空間とも呼ばれる）は、Hue（色相）、Saturation（彩度）と、HSLではLightness, Luminance（輝度）、HSVではValue（明度）の3つの成分からなる色空間であり、RGB色空間の非線形変換である。1970年代に、人間が色を知覚する方法により近い方法で色を表現できるよう設計された。2つの色空間はともに、上端が白で下端が黒の軸を中心に、各色相の中間色が放射状に配置された円柱形をしている。

HSL色空間における色の表現方法は、感覚的には絵具を混ぜて色を作る方法に近く、Lightnessの変化は、黒または白の絵具の量の変化に似ている。

例えば、「明るい赤」を作るためには赤の絵具に白の絵具を加えるが、このとき白の絵具を加えることはLightnessを大きくすることに相当する。HSL色空間において、純色は Lightness 50% の円周上の色であり、完全な黒と白はそれぞれ Lightness 0% と Lightness 100% の部分である。

一方、HSV色空間による色の表現方法は、光の下での色の見え方に近い。HSL色空間でLightnessが最大の色は「白」であるが、HSV色空間でValueが最大の色は、純色の物体に白色光を当てたときの色であるといえる。例えば、赤い物体に明るい白色光を当てると物体は「赤く」見え、白色光を暗くしていくと、物体は黒色に近づいて見える、ということに似ている。

これらの色空間では、3つの色成分が人間の色に対する知覚特性に十分には従っていないことが問題として指摘されることがある。これは、Lightness・Valueを固定してHueを変化させると顕著である。例えば、純色の青   と純色の黄色   は、HSLではともに Lightness 50% 、HSVではともに Value 100% であるが、青よりも黄色のほうがはるかに明るく感じられる。

基本となる考え方

図2a：HSL色空間を表す円柱

図2b：HSV色空間を表す円柱

HSLとHSVはともに円柱形の空間である（図2）。Hueは0度の原色の赤から始まり、120度の緑、240度の青を経て、360度すなわち0度の赤へと1周する。円柱の中心軸はともに、 Lightness 100% あるいは Value 100% の白の上端から、 Lightness 0% あるいは Value 0% の黒の下端、そしてその2色間を補完する灰色からなる。

どちらの色空間においても、加法混合の三原色と減法混合の三原色（赤、黄色、緑、シアン、青、マゼンタ）、そしてこれらの隣接するペアの間の線形混合色（純色）が、 Saturation 100% で円筒の最も外側に配置される。純色は、HSLでは Lightness 50% 、HSVでは Value 100% である。

純色に黒を混ぜても、HSL・HSVともにSaturationは変化しない。一方、純色に白を混ぜる場合、HSLではSaturationは変わらないが、HSVでは小さくなる。HSLのSaturationは、黒と白を同時に混ぜる場合に小さくなる。

図3aと図3b：HSLのLightnessに対して（図3a）、またはHSVのValueに対して（図3b）、SaturationではなくChroma（RGBの値の範囲）をプロットした場合、それぞれの空間は双円錐、円錐となる。このような図では、しばしば「Chroma」が「Saturation」と混同され、HSLやHSVの空間を直接表現したものであると主張される。

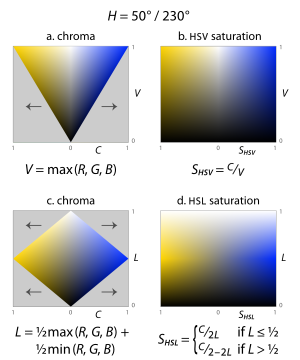
このような彩度の定義では、暗い色（両モデルとも）や明るい色（HSLの場合）も「Saturation 100%」すなわち「最も鮮やかな色」とされ、「Saturation（彩度）」を「鮮やかさ」としてとらえる場合、直感に反する。そこで図3のように、円柱の代わりに、半径方向にChroma（ある色をRGB色空間で表した際のその値の範囲に等しい。詳細は後述される）をとる円錐や双円錐を用いて色空間を表現することがある。このとき、半径方向の値が「Saturation」「彩度」と表現され、「Chroma」との区別が曖昧にされる場合がある。

後述されるように、Chromaの算出は、RGBからのHSL・HSVへの変換において有用である。

歴史

図4：古くから用いられてきた色の調合方法を簡易的に示した図。純色に対して白を加えたものを明清色、黒を加えたものを暗清色、白と黒の両方（すなわち灰色）を加えたものを中間色という。

図5：ドイツの化学者ヴィルヘルム・オストワルトによる色モデル（オストワルト表色系）。白または黒との混色というHSLに近いアプローチを示しており、24の色相を三角形で表し、環状に配置している。

HSL色空間は、1938年にフランスの技術者ジョルジュ・ヴァレンシによって、白黒の（輝度信号のみを放送する）テレビジョン放送に色の情報を付加する方法として開発された。このような方法はNTSC、PAL、SECAMなど主要なアナログテレビ放送やデジタルテレビ放送で使用されており、コンポジット映像信号の基礎となっている。

テレビ、パソコン、プロジェクターの多くは、赤、緑、青の3色の光を、強さを変えながら組み合わせることで色を表現する（加法混色）。しかし、十分に経験のない者や、絵具による混色（減法混色）に基づく色の表現に慣れている者は、この方法では容易には色を表現できない。より直感的な混色に対応するため、1970年代半ば、パロアルト研究所とニューヨーク工科大学の研究者らは、コンピューターのディスプレイ技術にHSV色空間を導入し、これはその後1978年8月の Computer Graphics 誌で、アルヴィ・レイ・スミスによって正式に記述された。

図6：テクトロニクスは、1979年にHSLを最も早く商用化した。この図は、テクトロニクスが1983年にアメリカ合衆国で出願した特許に添付された、HSLの双円錐の形状を示した図。

翌1979年には、テクトロニクスが色の指定にHSLを用いたグラフィックス端末をSIGGRAPHで発表した。HSLはRGBよりも直感的であるという点だけでなく、RGBとの変換が高速で可能であり、1970年代のコンピューターでもリアルタイムで相互に変換可能であった点でも便利であった。

以上の背景から、HSLや類似の色空間は、後述のように画像編集やグラフィックソフトウェアで広く使用されるようになった。

RGBからの導出

図7：HSL・HSVの円柱モデルとLCH色空間の、RGBからの幾何学的な導出を表現した図。

RGB立方体とHSV円柱の幾何学的な変換を視覚化した動画。

RGB立方体とHSL円柱の幾何学的な変換を視覚化した動画。

色を構成する属性

→「色覚」も参照

HSL色空間やHSV色空間の表現に用いられる値は、国際照明委員会などによって定義される同名の学術的な概念と直接関係するわけではない。しかし、初めにそのような概念について確認しておくことは有益である。

色相（Hue）

ある領域が、知覚される色（例えば赤、黄、緑、青）、あるいはそれらの2色の組み合わせに近いように見えるということに関する視覚的属性。

Radiance, L_e,Ω（放射輝度）

単位立体角あたり、単位投影面積あたりの放射束。SI単位は ワット毎ステラジアン毎平方メートル （W sr⁻¹ m⁻²）。

輝度（Luminance, Y または L_v,Ω）

放射輝度を波長ごとに重みづけして表される心理物理量。SI単位は カンデラ毎平方メートル （cd m⁻²）。輝度という用語は、 Y_n を基準の白とする相対輝度 Y/Y_n を指して用いられることがある。

ルーマ（Luma, Y'）

ガンマ補正された R', G', B' 値の加重和で、Y'CbCrでのJPEGファイルの圧縮や映像信号処理に利用される。

ブライトネス（Brightness）

光源色における色の明るさの尺度。物理学的にいうと光の強度であり、上限がない。単に「明るさ」と訳されることもある。

明度（Lightness または Value）

同じ照明を受けて白色に見える領域の明るさに対する、ある領域の相対的な明るさ。物理学的にいうと物体の分光反射率に対応するため、1あるいは100という上限がある。物体色のみに使用される明るさの尺度。

カラフルネス（Colorfulness）

色の鮮やかさ（色の強さ）の尺度。クロマや彩度/飽和度が相対的な尺度であるのに対し、カラフルネスは絶対的な色みの量の尺度である。

クロマ（Chroma）

マンセル表色系における色の鮮やかさ（色の強さ）の尺度。同じ明度の無彩色と比較した色みの量。絶対的な色みの量であるカラフルネスとは異なり、相対的な尺度である。

彩度・飽和度（Saturation）

ある領域のブライトネスに対して感じられる相対的なカラフルネス。または明度に対して感じられる相対的なクロマ。

明度（Lightness）とクロマ（Chroma）がある白色の領域を基準として相対的に定められる指標であるのに対し、ブライトネス（Brightness）とカラフルネス（Colorfulness）は、通常、目に到達する光のスペクトル分布などの物理的特性を表す絶対的な指標である。周囲の照明の変化によってブライトネスとカラフルネスは変化するのに対し、明度とクロマはあまり変動しないため、物体表面の色の表現には後者がしばしば用いられる。彩度・飽和度（Saturation）は、ブライトネスに対するカラフルネスの比、あるいは明度に対するクロマの比のどちらとしても定義されうる。

これ以降、特に明記されない限り、Hue、Saturationなどの単語はこれらの学術的な用語とは異なるものとする。

基本的な考え方

HSL、HSVやそれらに関連する色空間は、幾何学的に導出することができる。そのような色空間は「一般化されたLHSモデル」のうちの特定の色空間であるといえる。

HSLとHSVの色空間を構築するには、まずRGB立方体（ R, G, B ∈ [0, 1] ）を、黒が原点、白がその真上になるよう傾け、黒と白を結ぶ軸の周りの角度について、赤を0度としてHueを定義する。その後、軸上でValueあるいはLightnessを定義し、さらに軸に直交する方向（水平方向）に軸を0、純色を1としてSaturationを定義する。

図8：HueとChromaは、RGB立方体を「Chromaticity plane（色度平面）」に投影することで定義される。

Hue（色相）とChroma（クロマ）の導出

HSL・HSVやそれに似た色モデルでは、Hueと、この記事でChromaと呼ぶ値を同様に算出するため、それらの値は各モデルで同一となる。

傾けたRGB立方体を黒と白を結ぶ軸に垂直な平面に投影すると、赤、黄、緑、シアン、青、マゼンタを頂点とする正六角形となる（図8）。ここで、平面の原点は黒とする。Hueは、赤の位置ベクトルと投影された点（ある色をRGB空間で示す点を平面に投影したもの）の位置ベクトルのなす角の大きさに近い値で、Chromaは、原点と投影された点の間の距離に近い値で、それぞれ表される。

これらの色空間におけるHueとChromaは、いずれも平面に投影された六角形を基準として定義される。Chromaは、ある色を示す位置ベクトルの大きさの、そのベクトルを延長して最も外側の六角形と交わる点と原点との間の距離に対する割合（図8下の六角形における OP/OP' ）である。この割合は、ある色の R, G, B の値のうちの最大値と最小値の差、すなわち R, G, B の値の範囲を指している。ここで最大値、最小値、Chromaをそれぞれ M, m, C とそれぞれおくと、

$M=\max(R,G,B)$

$m=\min(R,G,B)$

$C=\operatorname {range} (R,G,B)=M-m$

Hueは、投影された点を通る六角形の辺の全周の長さに対する、投影された点までの辺の長さの割合であり、当初は0以上1以下の値で定義されたが、現在では一般的に0度以上360度未満の角度で定義される。原点に投影される点（白、黒とその間を補完する灰色）に対しては、Hueは定義されない。数学的には、このことは次のように区分的に定義される。

$H^{\prime }={\begin{cases}\mathrm {undefined} ,&{\text{if}}~~C=0\\{\frac {G-B}{C}}{\bmod {6}},&{\text{if}}~~M=R\\{\frac {B-R}{C}}+2,&{\text{if}}~~M=G\\{\frac {R-G}{C}}+4,&{\text{if}}~~M=B\end{cases}}$

$H=60^{\circ }\!\times H^{\prime }$

図9：HSLとHSVのHueとChromaの定義から、六角形を円に変形する図。

便宜上、無彩色のHueを0度とすることもある。

図10：極座標変換より導出された H₂, C₂ では、六角形から円へ変形した場合の H, C との間にずれが生じる。

これらの定義から、六角形の各辺を60度の円弧にマッピングすることで、六角形を円に変換することができる。このような変換を行うと、Hueは原点周りの角度、Chromaは原点からの距離、すなわちある色の位置ベクトルが赤の位置ベクトルに対してなす角と、そのベクトルの大きさでそれぞれ正確に表せる。

画像解析ソフトでは、上述のような変形の代わりに、HueとChroma（それぞれ H₂, C₂ とおく）を直交座標の極座標変換によって定義することがある（図10）。これは、 αβ 座標を用いて次のように行うことができる。

$\alpha =R-G\!\cdot \!\cos(60^{\circ })-B\!\cdot \!\cos(60^{\circ })={\frac {1}{2}}(2R\!-\!G\!-\!B)$

$\beta =G\!\cdot \!\sin(60^{\circ })-B\!\cdot \!\sin(60^{\circ })={\frac {\sqrt {3}}{2}}(G-B)$

$H_{2}=\operatorname {atan2} (\beta ,\alpha )$

$C_{2}=\operatorname {gmean} (\alpha ,\beta )={\sqrt {\alpha ^{2}\!+\beta ^{2}}}$

ここで、atan2は2つの引数をとるarctanであり、直交座標の2成分から角度を計算する。

この方法と円への変形とを比較すると、Hue（ H と H₂ ）はほぼ一致しており、どの色においてもその差は最大で約1.12度である（ H ≒ 13.38°, H₂ ≒ 12.26° などの12か所で差が最大となり、30度の倍数では H = H₂ ）。しかし、Chroma（ C と C₂ ）については、Hueが60度の倍数となる位置では両者は等しいが、30度の倍数であるときには約13.4%の差が生じる（例えば H = H₂ = 30° のとき C = 1 に対して C₂ = √¾ ≒ 0.866）。

図11aからd：あるHue（50度と230度）の面において、明るさを表す4種類の次元とChromaの関係を示した図。

明るさを表す成分の導出

Hueの定義は比較的一貫しているのに対し、明るさを表す成分の定義はモデルによって分かれる。ここでは、一般的な4種類の定義を示す（図11。これらのうち3つは図7にも示されている）。

• HSI色空間では、Intensity（強度）は R, G, B の平均値として定義される。これは、傾けたRGB立方体の軸に、ある色の点を投影したときの垂直方向の高さに等しい。この定義では、ある色のRGB立方体における幾何学的な情報を、Hue、Chromaとあわせて保持できるという利点がある。

  $I=\operatorname {avg} (R,G,B)={\frac {1}{3}}(R\!+\!G\!+\!B)$

• HSV色空間（図7の「Hexcone」モデル）では、Value（明度）は R, G, B の最大値として定義される。この定義では、赤、黄色、緑、シアン、青、マゼンタの全てが白と共通の平面上に位置する。

  $V=\max(R,G,B)=M$

• HSL色空間（図7の「Double Hexcone」モデル）では、Lightness（輝度）は R, G, B の中間値として定義される。この定義では、赤、黄色、緑、シアン、青、マゼンタを同一平面上に配置するものの、その平面は白と黒の中間を通る。

  $L=\operatorname {mid} (R,G,B)={\frac {1}{2}}(M+m)$

• より人間の知覚に近づけるための方法として、明るさの指標にルーマ（Y'）を用いる方法がある。ルーマは人間の知覚に基づいてガンマ補正された R, G, B の加重平均であり、カラーテレビ放送の白黒成分の次元として用いられている。sRGBでは Rec. 709 に基づくY'₇₀₉、NTSCでは Rec. 601 に基づくY'₆₀₁が用いられるなど、定義と用途はさまざまである。

  $Y_{\text{601}}^{\prime }=0.299~R+0.587~G+0.114~B$ (SDTV)

  $Y_{\text{240}}^{\prime }=0.212~R+0.701~G+0.087~B$ (Adobe RGB)

  $Y_{\text{709}}^{\prime }=0.2126~R+0.7152~G+0.0722~B$ (HDTV)

  $Y_{\text{2020}}^{\prime }=0.2627~R+0.6780~G+0.0593~B$ (UHDTV, HDR)

図12aからd：HSLとHSVでは、HueとLightness・Valueの全ての組み合わせに対して有意義なSaturationが定義されるよう、Chromaを拡張する。

Saturation（彩度）の導出

Hue・Chroma・LightnessやHue・Chroma・Valueによって色を表現するモデルでは、0度以上360度未満の H 、0以上1未満の C 、0以上1未満の V で表現できる色のうちの半分がRGB色域外（図14a、図14cの灰色に塗られた部分）であるため、Lightness（またはValue）とChromaの組み合わせがすべて有意義なわけではない。

これをより実用的にするため、HSLとHSVでは、HueとLightness・Valueがどのような組み合わせでも常に0以上1未満に収まるような新たな属性「Saturation（彩度）」を定義する。Saturationは、ある色のChromaを、その色のLightnessまたはValueで割ったものであり、HSLにおけるSaturationを S_L 、HSVにおけるSaturationを S_V とおいて次のように定義される。

$S_{L}={\begin{cases}0,&{\text{if}}~~L\!=\!1~~{\text{or}}~~L\!=\!0\\{\frac {C}{1-\vert 2L-1\vert }},&{\text{otherwise}}\end{cases}}$

$S_{V}={\begin{cases}0,&{\text{if}}~~V=0\\{\frac {C}{V}},&{\text{otherwise}}\end{cases}}$

図13a, b：HSIにおける「Saturation」（図13b）は、Saturationの定義「Lightnessに対するChroma」におおよそ対応する。また、図13aのような H₂, I, C₂ によるモデルも用いられる。これらの断面の真の「Hue」は図11, 12と同じであるが、成分 H, H₂ は計算方法の違いによって異なっている。

一方、コンピュータビジョンの分野で一般的に用いられるHSIモデルはHueを H₂ 、明るさの成分を I とするもので、HSLやHSVのように円柱を「埋める」ようなChromaの操作を行わない。代わりにHSIにおけるSaturationは、精神測定的な定義である「Lightnessに対するChroma」に沿って定義される（図13b）。これは、HSIが、色選択インターフェースの提供よりも、画像内の形状の分離を容易にすることを主な目的としているためである。画像解析における利用の項目も参照されたい。

$S_{I}={\begin{cases}0,&{\text{if}}~~I=0\\1-{\frac {m}{I}},&{\text{otherwise}}\end{cases}}$

これら3種類のモデルで、定義や実態が異なるにもかかわらず「Saturation」という同名の成分を用いていることは、しばしば混乱の元となる。HSVとHSIでは、この成分は「ある色自身のLightnessに対するChroma」という精神測定的な定義に近いが、HSLではそうではない。さらに、「Saturation（彩度）」という単語は、この記事でChromaと呼ぶ値（ C や C₂ ）に対してもよく用いられる。

実例

以下に示される値は、 H と H₂ が0度以上360度未満であることを除き、すべて0以上1以下である。

Color	R	G	B	H	H2	C	C2	V	L	I	Y′601	SHSV	SHSL	SHSI
5000000000000000000♠ FFFFFF	1.000	1.000	1.000	n/a	n/a	0.000	0.000	1.000	1.000	1.000	1.000	0.000	0.000	0.000
7000100000000000000♠ 808080	0.502	0.502	0.502	n/a	n/a	0.000	0.000	0.502	0.502	0.502	0.502	0.000	0.000	0.000
7000200000000000000♠ 000000	0.000	0.000	0.000	n/a	n/a	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
7000300000000000000♠ FF0000	1.000	0.000	0.000	5000000000000000000♠0.0°	5000000000000000000♠0.0°	1.000	1.000	1.000	0.500	0.333	0.299	1.000	1.000	1.000
7000400000000000000♠ BFBF00	0.749	0.749	0.000	7001600000000000000♠60.0°	7001600000000000000♠60.0°	0.749	0.749	0.749	0.375	0.499	0.664	1.000	1.000	1.000
7000500000000000000♠ 008000	0.000	0.502	0.000	7002120000000000000♠120.0°	7002120000000000000♠120.0°	0.502	0.502	0.502	0.251	0.167	0.295	1.000	1.000	1.000
7000600000000000000♠ 80FFFF	0.502	1.000	1.000	7002180000000000000♠180.0°	7002180000000000000♠180.0°	0.498	0.498	1.000	0.751	0.834	0.851	0.498	1.000	0.398
7000700000000000000♠ 8080FF	0.502	0.502	1.000	7002240000000000000♠240.0°	7002240000000000000♠240.0°	0.498	0.498	1.000	0.751	0.668	0.559	0.498	1.000	0.249
7000800000000000000♠ BF40BF	0.749	0.251	0.749	7002300000000000000♠300.0°	7002300000000000000♠300.0°	0.498	0.498	0.749	0.500	0.583	0.457	0.665	0.498	0.570
7000900000000000000♠ A0A424	0.627	0.643	0.141	7001619000000000000♠61.9°	7001616000000000000♠61.6°	0.502	0.494	0.643	0.392	0.471	0.581	0.780	0.640	0.700
7001100000000000000♠ 411BEA	0.255	0.106	0.918	7002251000000000000♠251.0°	7002249900000000000♠249.9°	0.812	0.748	0.918	0.512	0.426	0.243	0.885	0.831	0.752
7001110000000000000♠ 1EAC41	0.118	0.675	0.255	7002134800000000000♠134.8°	7002133690000099999♠133.7°	0.557	0.502	0.675	0.396	0.349	0.460	0.826	0.703	0.663
7001120000000000000♠ F0C80E	0.941	0.784	0.055	7001494000000000000♠49.4°	7001505000000000000♠50.5°	0.886	0.819	0.941	0.498	0.593	0.748	0.942	0.890	0.907
7001130000000000000♠ B430E5	0.706	0.188	0.898	7002283800000000000♠283.8°	7002284800000000000♠284.8°	0.710	0.636	0.898	0.543	0.597	0.424	0.790	0.777	0.685
7001140000000000000♠ ED7651	0.929	0.463	0.318	7001142000000000000♠14.2°	7001131000000000000♠13.1°	0.612	0.554	0.929	0.624	0.570	0.586	0.658	0.813	0.443
7001150000000000000♠ FEF888	0.996	0.973	0.533	7001569000000000000♠56.9°	7001574000000000000♠57.4°	0.463	0.451	0.996	0.765	0.834	0.930	0.465	0.983	0.361
7001160000000000000♠ 19CB97	0.098	0.796	0.592	7002162500000000000♠162.5°	7002163500000000000♠163.5°	0.698	0.622	0.796	0.447	0.495	0.564	0.877	0.781	0.802
7001170000000000000♠ 362698	0.212	0.149	0.596	7002248400000000000♠248.4°	7002247400000000000♠247.4°	0.447	0.419	0.596	0.373	0.319	0.219	0.750	0.600	0.533
7001180000000000000♠ 7E7EB8	0.494	0.494	0.722	7002240000000000000♠240.0°	7002240000000000000♠240.0°	0.227	0.227	0.722	0.608	0.570	0.520	0.315	0.290	0.133

ソフトウェアにおける利用

→「グラフィックソフトウェア」も参照

図14：HSV（HSB）を採用している色選択ツールの一例。この例では、Hue, Value（Brightness）は1つの面（円柱側面）で、Saturationはスライダーでそれぞれ選択できるようになっている。

HSLやHSVのようなモデルは、グラフィックソフトウェアなどにおける色選択ツールでしばしば用いられる。最も簡単なものでは各属性に対して1つ、計3つのスライダーが用意されているが、ほとんどの場合、モデルの2次元断面を表示し、どの断面を表示するかをスライダーで選択するようになっている（図14）。後者のGUIは、円柱、六角柱、円錐、双円錐などのモデルの形状に応じて様々に表示される。今日のコンピューター上の色選択ツールは、そのほとんどが、少なくともオプションとしてHSLやHSVを採用している。また、HSLやHSVの属性に基づいて色の組み合わせを提案するようなものも存在する。

色選択を要するほとんどのウェブアプリケーションは、HSLまたはHSVをベースとしたツールを使用しており、主要なウェブフロントエンド フレームワークの多くに、オープンソースの色選択ツールが含まれている。CSS3の仕様では、開発者が色の指定にHSLの値をそのまま利用できる。

HSLとHSVは、地図や医療画像などにおいて、データ可視化のためのグラデーションを定義するために利用されることがある。例えば、GISプログラムであるArcGISは、カスタマイズ可能なHSVベースのグラデーションを地理データに適用している。

画像編集ソフトには、HSLやHSV、あるいはIntensityやLumaに基づくモデルを利用して色を調整する機能をもつものがある。特に、色相と彩度のスライダーをもつツールは、少なくとも1980年代後半から一般的になっているが、より複雑なツールも様々に実装されている。

動画編集ソフトでも、これらのモデルは用いられる。例えば、Avidや Final Cut Pro には、HSLまたは類似のモデルに基づく色編集ツールがあり、動画の色の補正に使用できる。

画像解析における利用

→「コンピュータビジョン」および「画像解析」も参照

HSL、HSV、HSI、またはそれらに関連する色モデルは、コンピュータビジョンや画像解析において、特徴検出や画像セグメンテーションのためによく利用される。これは、物体検出、顔認識、文字認識、画像検索や医用画像の解析などで活用される。

カラー画像に使用されるコンピュータビジョンのアルゴリズムには、k平均法やファジィクラスタリング、Canny法など、グレースケール画像用に設計されたアルゴリズムをそのまま拡張したものがあり、最も単純な例では、色の成分ごとにこれらのアルゴリズムが適用される。このような場合には、RGB成分よりも、色相、明度、彩度のような成分を利用する方がより適切であることが多い。

1970年代後半から、特徴検出に対する有効性と計算量の少なさから、HSVやHSIのようなモデルへの色空間の変換が利用されてきた。物体の検出を目的とするならば色相、明度、彩度を大まかに分けるだけで十分であり、人間の色彩に対する知覚を厳密に再現する必要は特にないと考えられたためである。

HSIは John Kender の1976年の修士論文で提案され、その後1980年に、大田友一らによって先述の極座標変換に近いモデルが使用された。これらのモデルはより複雑なモデルよりも計算が簡単であり、性能も十分であることから、近年でも広く利用され続けている。

欠点

図15a：sRGB色域をCIELAB色空間に配置した図。 R, G, B で色相は等間隔でなく、原点からの距離も異なる。また、それぞれの L* の値も異なる（知覚的な明るさが異なる）。

図15b：Adobe RGB 色域をCIELAB色空間に配置した図。sRGB同様、 R, G, B の知覚的な関連は強くないことがわかる。

HSL、HSVやそれらに関連する色空間は、例えば単色を選択する程度であれば十分な機能を果たすものの、色の詳細な情報の多くを無視する。1970年代の画像処理装置や、1990年代の一般向けコンピューターなどでは、色の知覚的な関連性と高速な計算を両立しなければならなかったことが、この問題の背景にある。

HSLとHSVはRGBの単純な変換であり、RGB立方体の R, G, B の頂点が無彩色の軸から等距離・等間隔で配置されるという、人間の知覚とは無関係な対称性を保持している。RGBの色域をLab色空間のような知覚的に均一な空間にプロットする（図15）と明らかであるが、赤、緑、青の知覚的な明るさや彩度はそれぞれ異なり、色相も等間隔でない。

また、変換されるRGB空間が用いるガンマ補正などの特性によって、HSLやHSVの値は変化する。

HSLとHSVによる色表現の人間の知覚との乖離は、画像からHue、Saturation、Lightness・Valueをそれぞれ抽出し、同名の学術的な定義と比較することで顕著となる。

図16aの画像は、sRGB色空間を用いたカラー画像である。図16bは CIELAB L*（sRGB色空間の元となったCIEXYZ色空間の色成分のうち、知覚的な明るさを示す無彩色輝度成分 Y のみに依存する量）によるグレースケール画像であり、これは元のカラー画像に近い明るさであると感じられる。図16cのLuma（ Y' ）による画像でも、彩度の高い部分ではやや異なって見えるが、似たように感じられる。一方、図16e, fはHSVのValue V 、HSLのLightness L によるグレースケール画像であるが、オリジナルの画像の明るさとは大きく異なるように見える。

図16a：sRGB色域によるカラー画像。

図16b：CIELAB L* によるグレースケール画像。カラー画像で感じられる明るさに近い。

図16c：Rec. 601 のLumaによるグレースケール画像。

図16d：HSIの I （R, G, B の平均値）によるグレースケール画像。

図16e：HSVの V によるグレースケール画像。

図16f：HSLの L によるグレースケール画像。

これらの色空間はいずれも人間の知覚と完全に一致しているわけではないが、特にHSVのValue V とHSLのLightness L では特にずれが大きい。HSVでは純色の青   と白   は同じValue（明度）であるが、人間の知覚では、純色の青の輝度は白の10%程度である（正確な割合は使用するRGB色空間の種類に依存する）。また、HSLでは、赤100%、緑100%、青90%の非常に明るい黄色   は、知覚に基づく定義では彩度が非常に低いにもかかわらず、Saturation（彩度）は純色の緑   と等しいものとされる。地図製作における視認性や色彩に関する専門家であるシンシア・ブリューワーは、このような状況について次のように指摘した。

コンピュータサイエンスは、HSVやHLSのような不十分なものを知覚空間に提供しました。あなたの使うソフトウェアのインターフェイスにも現れるかもしれません。HSVやHLSはRGBの単純な数学的な変換ですが、Hue、LightnessあるいはValue、Saturationという用語を使っているために、あたかも知覚的なシステムのように見えます。しかし、よく見てください。騙されてはいけません。

知覚的な色の次元は、これらや他のいくつかの仕組みでは、適切には尺度化されていません。例えば、SaturationとLightnessは混同されており、「Saturation（彩度）」という尺度に幅広い（知覚的な）明るさも含まれていることがあります（例えば、（知覚的な）彩度と（知覚的な）明るさがともに変わるはずの白から緑への移動が可能です）。HueとLightnessも混同されています。例えば、純色の黄色と純色の青は同じ「Lightness（輝度・明るさ）」であるとされますが、知覚的な明るさは大きく異なります。

このような欠陥が、体系的な方法で配色をコントロールすることを困難にしています。望ましい効果を得るために多くの微調整が必要であれば、RGBやCMYの生の仕様と格闘することに対する利益は、ほぼありません。

このようなことによってHSLやHSVが色選択の場面で問題を抱えているとすると、画像補正にはより不向きであるといえる。HSLとHSVは、ブリューワーが述べるように知覚的な色の属性を混同しているため、1つの値を変更すると、3つの知覚的な属性すべてに不均一な変化が生じ、画像全体の色関係が歪んでしまう。例えば、濃紺色のHue（色相）を緑色に近づくように変更する（例えば   から   ）と、知覚的な彩度は低下し、知覚的な明るさは増加する（すなわち、より灰色みが強まり、明るくなったように見える）が、より明るい青みの緑から同じ角度だけHueを変更した場合（例えば   から   ）では全く逆に、知覚的な彩度が増加し、知覚的な明るさが減少する（すなわち、より鮮やかになり、暗くなったように見える）。

下の図17の例では、図17aのオリジナルの画像に対し、図17bでHSLのSaturationとLightnessあるいはHSVのSaturationとValueを一定に保ってHueを−30度回転し、図17cではCIELABの輝度（ L* 、すなわち知覚的な明るさの近似値）を一定に保って同じHueの回転（−30度）を施している。図17bでは、亀の甲羅はより暗く、背景はより明るくなっているように見えるなど、知覚的な明るさに関して大きな違いが表れている。

図17a：カラー画像。

図17b：HSL・HSVのHueを−30度回転させた画像。

図17c：知覚的な明るさを保ったままHueを−30度回転させた画像。

Hueは360度で不連続な円形の量であるため、単純な計算や定量的な比較が難しい。また、Hueは60度ごとに区分的に定義され、R, G, B に対するLightness・Value、Saturationの関係は、その区分に依存して決定される。この定義では、HSLやHSVの水平断面で見られる不連続性が生じる。

デジタル映像分野の専門家であるチャールズ・ポイントンは、HSLやHSVに関する上述のような問題点について、次のように結論づけている。

HSBとHLSは、ユーザーが色を数値的に指定しなければならなかった時代に、色相と彩度とブライトネス（あるいは色相と明度と彩度）を数値で指定するために開発されました。HSBとHLSの一般的な変換式には、色覚特性に関して欠陥があります。ユーザーが色を視覚的に選んだり、別の手段に関連付けられた色を選んだり（例えばPANTONE）、あるいはL*u*v*やL*a*b*のような知覚に基づく仕組みを使ったりできるようになった現在では、HSBやHLSは放棄されるべきでしょう。

円筒座標系を用いる他の色モデル

→詳細は「en: Color model § Cylindrical-coordinate color models」、および「en: List of color spaces and their uses § Cylindrical transformations」を参照

HSLやHSVは、無彩色の軸とその周りの角度に対応する色相をもつ円錐または球形の色モデルとしては、最初のものではない。同様のモデルは18世紀から現在に至るまで開発が続いている（図5のオストワルト表色系など）。

異なる色モデル間の数学的な変換

方針

HSLまたはHSVからRGBへ変換するためには、基本的には上述の手順を反転する。その際も、 R, G, B ∈ [0, 1] である。

まず、与えられた色のLightnessまたはValueにおけるChromaの最大値をSaturationの値に乗じることにより、Chromaを計算する。次に、RGB立方体の底面3面のうち、与えられた色と同じHueとChromaをもつ、すなわち色度平面上の同じ点に投影される点を探す。最後に、与えられた色のLightnessまたはValueに一致するよう、 R, G, B に等量を加算する。

RGBへの変換

HSLからRGBへ

Hueを H ∈ [0°, 360°) 、Saturationを S_L ∈ [0, 1] 、Lightnessを L ∈ [0, 1] とする。

まず、次のようにしてChroma C を求める。

$C={\big (}1-\vert 2L\!-\!1\vert {\big )}\times S_{L}$

ただし、円錐モデルではSaturationの値として実際にはChromaを用いているため、変換は必要ない。

$C=S_{L}$

次に、RGB立方体の底面3面において、与えられた色と同じHue、Chromaをもつ点 (R₁, G₁, B₁) を求める。この操作のために、 H', X を次のように定義する。

$H^{\prime }={\frac {H}{60^{\circ }\!}}$

$X=C\times {\big (}1-{\big \vert }(H^{\prime }\!{\bmod {2}})-1{\big \vert }{\big )}$

ここで、 (H' mod 2) は H' を2で割った余りである。 H' は整数でなくてもよい。

$(R_{1},G_{1},B_{1})={\begin{cases}(0,0,0)&{\text{if}}~H~{\text{is undefined}}\\(C,X,0)&{\text{if}}~~0\leqq H^{\prime }\!<1\\(X,C,0)&{\text{if}}~~1\leqq H^{\prime }\!<2\\(0,C,X)&{\text{if}}~~2\leqq H^{\prime }\!<3\\(0,X,C)&{\text{if}}~~3\leqq H^{\prime }\!<4\\(X,0,C)&{\text{if}}~~4\leqq H^{\prime }\!<5\\(C,0,X)&{\text{if}}~~5\leqq H^{\prime }\!<6\end{cases}}$

最後に、Lightnessを合わせるために R₁, G₁, B₁ それぞれに m を加えると、 R, G, B が求められる。

$m=L-{\frac {C}{2}}$

$(R,G,B)=(R_{1}\!+m,~G_{1}\!+m,~B_{1}\!+m)$

HSLからRGBへ（簡略化）

上記の区分的に定義された関数は、最小値、最大値、剰余の演算を活用して簡略化できる。

Hueを H ∈ [0°, 360°) 、Saturationを S_L ∈ [0, 1] 、Lightnessを L ∈ [0, 1] とし、まず次の関数 f(n) を定義する。

$f(n)=L-a\!\cdot \!\max \!{\big (}{-1,~\min(k\!-\!3,~9\!-\!k,~1)}{\big )}$

ただし、 k, n はともに0以上の実数であり、 k, a は次のように定義される。

$k={\Big (}n+{\frac {H}{30^{\circ }\!}}{\Big )}{\bmod {1}}2$

$a=S_{L}\!\times \min(L,~1\!-\!L)$

ここで、 k ∈ [0, 12) となる。

これらのもとで、R, G, B の値（それぞれ0以上1以下）が次のように得られる。

$(R,G,B)={\big (}f(0),~f(8),~f(4){\big )}$

ここで、 f(n) のうち ${\textstyle \max \!{\big (}{-1},~\min(k\!-\!3,~9\!-\!k,~1){\big )}}$ の部分は、 H, S, V と R, G, B の関係性を表すグラフ（図18）の基本形状を表している。これは k の関数であり、k は n, H の関数であるから、 ${\textstyle t(n,H)=T(k)=\max \!{\big (}{-1},~\min(k\!-\!3,~9\!-\!k,~1){\big )}}$ と表せる。これは、次のように構成される。

$t_{1}=\min(k\!-\!3,~9\!-\!k)$ は、 k = 6 で直線を折り返す上に凸のグラフを描く。ここで $t_{2}=\min(t_{1},~1)$ 、さらに $t=\max(t_{2},-1)=\max \!{\big (}{\min(t_{1},~1),-1}{\big )}$ とし、 t の範囲を−1以上1以下に制限する。このとき、このグラフは図18の R のグラフを上下反転したような形をしている。

関数 f(n) では、 n によって x 方向の平行移動、 −a 倍によって y 方向の拡大縮小、 L によって y 方向の平行移動を行い、 R, G, B それぞれのグラフを得ている。

HSVからRGBへ

図18：HSVとRGBの値の関係を示した図。

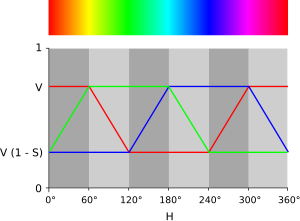
Hueを H ∈ [0°, 360°) 、Saturationを S_V ∈ [0, 1] 、Valueを V ∈ [0, 1] とする。

まず、次のようにしてChroma C を求める。

$C=V\times S_{V}$

ただし、双円錐モデルではSaturationの値として実際にはChromaを用いているため、変換は必要ない。

$C=S_{V}$

次に、RGB立方体の底面3面において、与えられた色と同じHue、Chromaをもつ点 (R₁, G₁, B₁) を求める。この操作のために、 H', X を次のように定義する。この操作は、HSLの場合と全く同じである。

$H^{\prime }={\frac {H}{60^{\circ }\!}}$

$X=C\times {\big (}1-{\big \vert }(H^{\prime }\!{\bmod {2}})-1{\big \vert }{\big )}$

$(R_{1},G_{1},B_{1})={\begin{cases}(0,0,0)&{\text{if}}~H~{\text{is undefined}}\\(C,X,0)&{\text{if}}~~0\leqq H^{\prime }\!<1\\(X,C,0)&{\text{if}}~~1\leqq H^{\prime }\!<2\\(0,C,X)&{\text{if}}~~2\leqq H^{\prime }\!<3\\(0,X,C)&{\text{if}}~~3\leqq H^{\prime }\!<4\\(X,0,C)&{\text{if}}~~4\leqq H^{\prime }\!<5\\(C,0,X)&{\text{if}}~~5\leqq H^{\prime }\!<6\end{cases}}$

最後に、Valueを合わせるために R₁, G₁, B₁ それぞれに m を加えると、 R, G, B が求められる。

$m=V-C$

$(R,G,B)=(R_{1}\!+m,~G_{1}\!+m,~B_{1}\!+m)$

HSVからRGBへ（簡略化）

Hueを H ∈ [0°, 360°) 、Saturationを S_V ∈ [0, 1] 、Valueを V ∈ [0, 1] とし、まず次の関数 f(n) を定義する。

$f(n)=V-VS\!\cdot \!\max \!{\big (}0,~\min(k,~4\!-\!k,~1){\big )}$

ただし、 k, n はともに0以上の実数であり、 k は次のように定義される。

$k={\Big (}n+{\frac {H}{60^{\circ }\!}}{\Big )}{\bmod {6}}$

ここで、 k ∈ [0, 6) となる。

これらのもとで、R, G, B の値（それぞれ0以上1以下）が次のように得られる。

$(R,G,B)={\big (}f(5),~f(3),~f(1){\big )}$

f(n) の特性は、 ${\textstyle t(n,H)=T(k)=\max \!{\big (}0,~\min(k,~4\!-\!k,~1){\big )}}$ として、HSLの場合と同様にして考察できる。

HSIからRGBへ

Hueを H ∈ [0°, 360°) 、Saturationを S_I ∈ [0, 1] 、Intensityを I ∈ [0, 1] とする。

$H^{\prime }={\frac {H}{60^{\circ }\!}}$

$Z=1-{\big \vert }(H^{\prime }\!{\bmod {2}})-1{\big \vert }$

$C={\frac {3\!\cdot \!I\!\cdot \!S_{I}}{1\!+\!Z}}$

$X=C\!\cdot \!Z$

ただし、 C はChromaである。

次に、RGB立方体の底面3面において、与えられた色と同じHue、Chromaをもつ点 (R₁, G₁, B₁) を求める。

$(R_{1},G_{1},B_{1})={\begin{cases}(0,0,0)&{\text{if}}~H~{\text{is undefined}}\\(C,X,0)&{\text{if}}~~0\leqq H^{\prime }\!\leqq 1\\(X,C,0)&{\text{if}}~~1\leqq H^{\prime }\!\leqq 2\\(0,C,X)&{\text{if}}~~2\leqq H^{\prime }\!\leqq 3\\(0,X,C)&{\text{if}}~~3\leqq H^{\prime }\!\leqq 4\\(X,0,C)&{\text{if}}~~4\leqq H^{\prime }\!\leqq 5\\(C,0,X)&{\text{if}}~~5\leqq H^{\prime }\!\leqq 6\end{cases}}$

最後に、Intensityを合わせるために R₁, G₁, B₁ それぞれに m を加えると、 R, G, B が求められる。

$m=I\!\cdot \!(1-S_{I})$

$(R,G,B)=(R_{1}\!+m,~G_{1}\!+m,~B_{1}\!+m)$

Luma, Chroma, Hue による色空間からRGBへ

Hueを H ∈ [0°, 360°) 、Chromaを C ∈ [0, 1] 、Lumaを Y'₆₀₁ ∈ [0, 1] とする。

$H^{\prime }={\frac {H}{60^{\circ }\!}}$

$X=C\times {\big (}1-{\big \vert }(H^{\prime }\!{\bmod {2}})-1{\big \vert }{\big )}$

$(R_{1},G_{1},B_{1})={\begin{cases}(0,0,0)&{\text{if}}~H~{\text{is undefined}}\\(C,X,0)&{\text{if}}~~0\leqq H^{\prime }\!\leqq 1\\(X,C,0)&{\text{if}}~~1\leqq H^{\prime }\!\leqq 2\\(0,C,X)&{\text{if}}~~2\leqq H^{\prime }\!\leqq 3\\(0,X,C)&{\text{if}}~~3\leqq H^{\prime }\!\leqq 4\\(X,0,C)&{\text{if}}~~4\leqq H^{\prime }\!\leqq 5\\(C,0,X)&{\text{if}}~~5\leqq H^{\prime }\!\leqq 6\end{cases}}$

Lumaを合わせるために R₁, G₁, B₁ それぞれに m を加えると、 R, G, B が求められる。

$m=Y_{601}^{\prime }\!-(0.30R_{1}+0.59G_{1}+0.11B_{1})$

$(R,G,B)=(R_{1}\!+m,~G_{1}\!+m,~B_{1}\!+m)$

相互変換

HSVからHSLへ

Hueを H ∈ [0°, 360°) 、Saturationを S_V ∈ [0, 1] 、Valueを V ∈ [0, 1] とする。

$H_{L}=H_{V}$

$L=V{\bigg (}1-{\frac {S_{V}}{2}}{\bigg )}$

$S_{L}={\begin{cases}0,&{\text{if}}~~L\!=\!1~~{\text{or}}~~L\!=\!0\\{\frac {V-L}{\min(L,~1-L)}},&{\text{otherwise}}\end{cases}}$

HSLからHSVへ

Hueを H ∈ [0°, 360°) 、Saturationを S_L ∈ [0, 1] 、Lightnessを L ∈ [0, 1] とする。

$H_{V}=H_{L}$

$V=L+S_{L}\min(L,~1\!-\!L)$

$S_{V}={\begin{cases}0,&{\text{if}}~~V\!=0\\2{\Big (}1-{\frac {L}{V}}{\Big )},&{\text{otherwise}}\end{cases}}$

RGBからの変換

→「HSL色空間とHSV色空間 § 基本的な考え方」も参照

ここに示される変換は、上述の導出方法と同じものである。 R, G, B ∈ [0, 1] とする。

最大値 X_max （すなわちValue V ）、最小値 X_min 、範囲（すなわちChroma） C 、中央値（すなわちLightness） L を、それぞれ次のように求める。

$X_{\textrm {max}}=V=\max(R,G,B)$

$X_{\textrm {min}}=\min(R,G,B)=V\!-C$

$C=X_{\textrm {max}}-X_{\textrm {min}}=2(V\!-L)$

$L=\operatorname {mid} (R,G,B)={\frac {X_{\textrm {max}}+X_{\textrm {min}}}{2}}=V-{\frac {C}{2}}$

Hue H はHSL、HSVで共通であり、次のように求められる。

$H:={\begin{cases}\mathrm {undefined} ,&{\text{if}}~~C=0\\60^{\circ }\!\times \!{\Big (}{\frac {G-B}{C}}{\bmod {6}}{\Big )},&{\text{if}}~~V=R\\60^{\circ }\!\times \!{\Big (}{\frac {B-R}{C}}+2{\Big )},&{\text{if}}~~V=G\\60^{\circ }\!\times \!{\Big (}{\frac {R-G}{C}}+4{\Big )},&{\text{if}}~~V=B\end{cases}}$

HSL、HSVそれぞれのSaturationは、次のように求められる。

$S_{V}={\begin{cases}0,&{\text{if}}~~V\!=0\\{\frac {C}{V}},&{\text{otherwise}}\end{cases}}$

$S_{L}={\begin{cases}0,&{\text{if}}~~L\!=\!1~~{\text{or}}~~L\!=\!0\\{\frac {C}{1-\vert 2V-C-1\vert }}={\frac {2(V-L)}{1-\vert 2L-1\vert }}={\frac {V-L}{\min(L,~1-L)}},&{\text{otherwise}}\end{cases}}$