負性抵抗

蛍光灯は負性微分抵抗を持つ素子の1つである。点灯中に蛍光灯に流れる電流が増加すると、両端の電圧は低下する。蛍光灯が送電線に直接つながれていると、電圧低下がさらなる電流増加を招き、アークフラッシュによって破壊されてしまう。これを防ぐため、蛍光灯は安定器を介して送電線に接続される。安定器は正のインピーダンスを追加することで蛍光灯の負性抵抗を打ち消し、電流を制限する。

電子工学において、負性抵抗（ふせいていこう、英: negative resistance, NR）は、一部の電気回路や素子が持つ特性で、端子間の電圧が増加すると、流れる電流が減少するものを指す。

負性抵抗の振る舞いは、印加電圧が増えるとオームの法則により電流が比例して増加し抵抗値が正となる通常の抵抗器とは対照的である。通常の抵抗器は、正の抵抗に電流が流れると電力を消費するが、負性抵抗は電力を発生する。負性抵抗は特定の条件下で電気信号の電力を増加させて増幅機能を担うことができる。

負性抵抗は限られた数の非線形電子素子でしか見られない。非線形素子では抵抗の定義が2種類ある。「静的抵抗」は電圧 $v$ の電流 $i$ に対する比 $v/i$ をいい、「微分抵抗」は電圧変化とそれによって生じた電流変化の比 $\Delta v/\Delta i$ をいう。負性抵抗という言葉は負性微分抵抗、すなわち $\Delta v/\Delta i\;<\;0$ を意味する。一般に負性微分抵抗は増幅機能を持つ2端子素子であり、端子に与えられた直流電力を交流出力電力に変換することで同じ端子に印加された交流信号を増幅することができる。電子発振器や増幅器の構成部品に用いられ、特にマイクロ波領域での利用が多い。マイクロ波領域のエネルギーは負性微分抵抗素子によって生み出されるのがほとんどである。負性抵抗素子はヒステリシス や双安定性を示すことがあり、スイッチングやメモリ回路にも利用される。負性微分抵抗を持つ素子の例にはトンネルダイオード、ガンダイオード、ネオン管などのガス放電管、蛍光灯がある。そのほかトランジスタもしくは正帰還を施したオペアンプのような増幅素子を含む回路にも負性微分抵抗を持たせることが可能であり、発振器やアクティブフィルタに利用されている。

負性抵抗素子は非線形であり、通常の電気回路で見られる正の「オーミックな」抵抗より動作が複雑になる。ほとんどの正抵抗とは異なり、負性抵抗素子の抵抗値は印加される電圧や電流によって変化し、限られた電圧・電流範囲でしか負の抵抗を持たない。すなわち、任意の電流範囲にわたって一定の負性抵抗を持つという意味で正の抵抗器に対応する「負性抵抗器」は存在しない。

ガンダイオード。負性微分抵抗を持つ半導体素子の一つで、マイクロ波を発生する電子発振器に利用される。

定義

図の I–V 曲線において、点Aでの「静的抵抗」は弦Bの勾配の逆数を言い、「微分抵抗」は接線Cの勾配の逆数を言う。

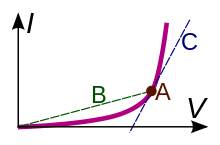
電気素子や電気回路の端子間抵抗は、端子間に任意の電圧 $v$ を印加したときに流れる電流 $i$ を与える特性曲線（ I–V 曲線）から決定される。電気回路に付随する通常の（正の）抵抗を初めとしてほとんどの材料はオームの法則に従っており、広い範囲にわたって電流と電圧が比例する。このようなオーミック抵抗の I–V 曲線は原点を通る正勾配の直線である。その抵抗値は電流に対する電圧の比であり、電圧 $v$ を独立変数とする I–V グラフでは直線の勾配の逆数に当たる。その値は一定で変わらない。

負性抵抗はある種の非線形素子（非オーミック素子）で見られる。非線形素子の I–V 曲線は直線ではなく、オームの法則は成立しない。その場合も抵抗を定義することは可能だが、値は一定ではなく素子に加わる電圧や電流によって移り変わる。そのような非線形素子の抵抗には2種類の定義がある。オーミック抵抗ではそれらは一致する。

I–V 平面は受動素子が属する象限（白）と能動素子が属する象限（赤）に分かれる。

• 静的抵抗（英: static resistance、または chordal resistance「弦抵抗」、absolute resistance「絶対抵抗」、または単にresistance「抵抗」）：抵抗の一般的な定義と同じく、電圧を電流で割った値をいう。

$R_{\mathrm {static} }={v \over i}$

原点から I–V 曲線上の点（図のA）まで引いた線分（弦）の勾配の逆数にあたる。

電池や発電機のような電源では正電圧端子から正の電流が流れ出す。これは抵抗器の正端子に電流が流れ込むのとは逆である。したがって受動素子の符号の規約により電源の $v$ と $i$ は逆符号となり、右図の I–V 平面では第2または第4象限の点で表される。このため電源は形式上負の静的抵抗を持つ（ $R_{\text{static}}\;<\;0$ ）。ただし「抵抗」という言葉は受動素子にのみ適用されるため実際には負性抵抗という呼び方はされない。静的抵抗は素子での電力散逸を決定する。電力を消費する受動素子は正の静的抵抗を持ち、電力を発生する能動素子はその逆となる。

• 微分抵抗（英: differential resitance、または dynamic resistance「動作抵抗」、incremental resistance「増分抵抗」）：電圧を電流で微分したもの。小さな電流変化に対する電圧変化の比であり、I–V 曲線の勾配の逆数に当たる。

$r_{\mathrm {diff} }={\frac {dv}{di}}$

微分抵抗は電流が時間変化する場合にのみ意味がある。勾配が負（右下がり）の点では電圧増加に対して電流が減少するので負性微分抵抗（$r_{\text{diff}}\;<\;0$）を持つことになる。このタイプの素子は信号を増幅することが可能であり、「負性抵抗」というと通常これを指す。

負性抵抗は正の抵抗と同じくオーム（Ω）単位で表される。

コンダクタンスとは抵抗の逆数をいう。その単位ジーメンス（旧称モー）は抵抗1 Ωの抵抗器が持つコンダクタンスを基準とする単位である。上述した2種類の抵抗はそれぞれ対応するコンダクタンスを持つ。

• 静的コンダクタンス

$G_{\mathrm {static} }={1 \over R_{\mathrm {static} }}={i \over v}$

• 微分コンダクタンス

$g_{\mathrm {diff} }={1 \over r_{\mathrm {diff} }}={di \over dv}$

これらの式が表すように、コンダクタンスは対応する抵抗と同じ符号となる。負の抵抗は負のコンダクタンスを、正の抵抗は正のコンダクタンスを持つ。

図1: 「オーミック」な線形抵抗の I–V 曲線。電気回路で通常みられる種類の抵抗である。電流は電圧に比例し、そのため静的抵抗と微分抵抗はどちらも正で値は等しい。 $R_{\text{static}}=r_{\text{diff}}={v \over i}>0$

図2: 一部（赤）で負性微分抵抗を持つ I–V 曲線。点Pにおける微分抵抗 $r_{\text{diff}}$ は接線の勾配の逆数

$r_{\text{diff}}={\frac {\Delta v}{\Delta i}}={\frac {v_{2}-v_{1}}{i_{2}-i_{1}}}$

になる。点Pにおいては $\Delta v>0$ かつ $\Delta i<0$ であるため $r_{\text{diff}}<0$ となる。

図3: 電源の I–V 曲線。第2象限（赤）において電流は正電極から流れ出すため、電気エネルギーは素子から回路に向けて与えられる。たとえば点Pは $v<0$ かつ $i>0$ であり、したがって $R_{\text{static}}={v \over i}<0$ である。

図4: 「能動抵抗」 とも呼ばれる負性線形抵抗（赤）の I–V 曲線。能動素子であるため静的抵抗は負となり、微分抵抗も同じく負である。

$R={\Delta v \over \Delta i}={v \over i}<0$

動作

抵抗を分類する方法の一つに、電流と電力が回路から素子に流れ込むのか、それとも流れ出すのかを見るものがある。下図にそれぞれのタイプの動作を示す。長方形が回路に接続された素子を表している。

電気素子の電圧 $v$ と電流 $i$ を定義するときは、受動素子の符号の規約に従って、正の電圧端子に流れ込む電流を正とするのが普通である。そのため電力 $P$ の符号は回路から素子にエネルギーが流れるときに正、素子から回路に流れるときに負となる。これは直流・交流のいずれでも成り立つ。右図は各変数の正の向きを示している。
正の静的抵抗では $R_{\text{static}}=v/i>0$ であるため $v$ と $i$ は同符号となる。上述の規約により、正電流は素子中を正端子から負端子へ向かって電界 E の向き（電位が低下する向き）に沿って流れる。$P=vi>0$ であるから、電荷は素子中で仕事を行ってポテンシャルエネルギーを失い、電力は回路から素子に与えられて 熱エネルギーなどに変換される（図の黄色い流れ）。印加電圧が交流であれば $v$ と $i$ は周期的に反転するが、瞬時電流は常に高電位から低電位に向けて流れる。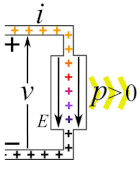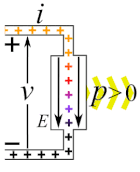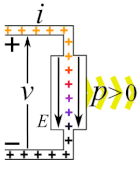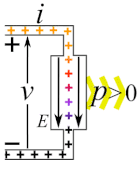
電源では $R_{\text{static}}=v/i<0$ であり、$v$ と $i$ は異符号となる。電流は素子中を負端子から正端子に向けて流れることになる。電荷がポテンシャルエネルギーを獲得するので、電力は素子から回路に向かって与えられる。つまり $P=vi<0$ である。電界の力に抗して電荷を動かすためには素子中の何らかの電力源が仕事を与えなければならない（図の黄色い流れ）。
受動的な負性微分抵抗では $r_{\text{diff}}=\Delta v/\Delta i<0$ であり、電流の交流成分が電圧の交流成分と逆の方向に流れる。静的抵抗は負にならない ので、正味の電流は正端子から負端子に向けて流れ、$P=vi>0$ となる。しかし電圧増加に対して電流が減少するため、交流電圧を直流電圧に重畳させて素子に加えると（図）、電流の時間変化成分 $\Delta i$ と電圧の時間変化成分 $\Delta v$ の符号が逆なので $P_{\text{AC}}=\Delta v\Delta i<0$ となる。つまり交流電流の瞬時値 $\Delta i$ は電圧の交流成分 $\Delta v$ が増加する向きに沿って素子を流れるので、交流電力は素子から回路に与えられる。素子は直流電力を消費するが、その一部を交流信号の電力として外部負荷に供給する。これによって素子は与えられた交流信号を増幅することができる。

種類と呼称

	$r_{\text{diff}}>0$ 正の微分抵抗	$r_{\text{diff}}<0$ 負の微分抵抗
$R_{\text{static}}>0$ 受動素子、正味の電力消費	正抵抗 抵抗器 一般的なダイオード ほとんどの受動素子	受動負性微分抵抗 トンネルダイオード ガン・ダイオード 気体放電管
$R_{\text{static}}<0$ 能動素子、正味の電力生成	電源 電池 発電機 トランジスタ ほとんどの能動素子	「能動抵抗」（以下の用途に用いられる正帰還増幅器） 帰還発振器 負性コンダクタンス変換器 アクティブフィルタ

電子素子の微分抵抗 $r_{\text{diff}}$と静的抵抗 $R_{\text{static}}$はそれぞれ単独でも同時にも負になりうるため、「負性抵抗」と呼ばれる素子は3つのカテゴリに分けられる（前掲の図2~4、および上の表を参照）。

ほとんどの場合「負性抵抗」という呼び方は負の微分抵抗、つまり $r_{\text{diff}}<0$ を意味する。負性微分抵抗素子には1ポート増幅器としてポート（端子対）に印加される時変信号の電力を増幅したり、同調回路に発振を励起して発振器となるという独自の性能がある。ヒステリシスを持つこともある。素子が負性微分抵抗を持つには何らかの電力源が必要であり、電力を内部電源から取るか、あるいはポートから取るかによって次の2つのカテゴリに分けられる。

• 受動的な負性微分抵抗素子（前掲の図2）最もよく知られているタイプの「負性抵抗」。受動2端子素子で、I–V 特性曲線には右下がりに折れ曲がった部分があり、そのため一部の動作範囲では電圧が上昇すると電流が減少する。I–V 曲線は負性抵抗領域を含めて I–V 平面の第1象限と第3象限に収まっており、静的抵抗は常に正。例としては気体放電管、トンネルダイオード、ガンダイオードがある。これらの素子は内部電源を持たず、一般に外部からポートに与えられた直流電力を交流電力に変換して動作するため、ポートには目的の信号と同時に直流バイアス電流を印加する必要がある。紛らわしいことに、一部の著者は この種の負性抵抗を増幅機能の存在から「能動」素子と呼んでいる。ユニジャンクショントランジスタなど、3端子素子の中にもこのカテゴリに含まれるものがある。詳しくは負性微分抵抗節で解説する。

• 能動的な負性微分抵抗素子（前掲の図4）端子に正電圧を印加すると（ある動作範囲で）それに比例する「負の電流」が発生するもの。回路設計によって実現できる。前項の受動素子とは異なり、I–V 曲線は原点を通過する部分が右下がりであるため I–V 平面の第2象限と第4象限にも伸びている。これは素子が電力を生成していることを表している。トランジスタや正帰還を備えたオペアンプのような増幅素子はこのタイプの負性抵抗を持つことができ、フィードバック発振器やアクティブフィルタに利用される。これらの回路はポートから正味の電力を生み出すため、内部に直流電源を備えるか、別に外部電源に接続する必要がある。回路理論では「能動抵抗」と呼ばれる。受動負性抵抗と区別するために「線形 (linear) 負性抵抗」、「絶対 (absolute) 負性抵抗」、「理想 (ideal) 負性抵抗」、「純粋 (pure) 負性抵抗」 と呼ばれることがあるが、電子工学では単にポジティブフィードバックもしくは再生回路と呼ばれることが多い。詳しくは能動抵抗節で解説する。

電池は通常の動作範囲で負の静的抵抗（赤）を持つが、微分抵抗は正である。

通常の電源が「負性抵抗」と呼ばれることもある（前掲の図3）。能動素子は静的抵抗が負になるのだが（負の静的抵抗節を参照）、電池や発電機、あるいは正帰還ではない増幅器など、ほとんどの電源は直流であれ交流であれ正の微分抵抗（内部抵抗）を持つ。したがってこれらは1ポート増幅器として機能するなどの特性を持たない。

負性抵抗素子の一覧

負性微分抵抗を持つ電子部品には以下が含まれる。

• トンネルダイオード や共鳴トンネルダイオード などトンネル現象を利用した半導体ダイオード
• ガン・ダイオード など電子遷移機構を利用したダイオード
• IMPATTダイオード やTRAPATTダイオードなど衝突電離機構を利用したダイオード
• NPNトランジスタのエミッタ-コレクタ間に逆バイアスを加えたネジスタ (negistor) と呼ばれる素子
• ユニジャンクショントランジスタ
• サイリスタ
• ダイナトロン発振器モードで動作させた三極真空管や四極真空管
• 一部のマグネトロン管などのマイクロ波真空管
• メーザー
• パラメトリック増幅器

気体中の放電も負の微分抵抗を示す。以下のデバイスは例である。

• アーク放電
• サイラトロン管
• ネオン灯
• 蛍光灯
• その他の気体放電管

そのほか、トランジスタやオペアンプなどの増幅素子にフィードバックをかけることで負性微分抵抗を持つ能動回路を構成できる。近年では負の微分抵抗を持つ材料や素子が研究レベルで多数発見されている。負性抵抗を発現させる物理的プロセスは多様であり、各種の素子はそれぞれ（ I–V 特性で表される）独自の特徴を持っている。

負の静的抵抗

正の静的抵抗は電力を熱に変換し、周囲を温める（左図）。しかし負の静的抵抗は逆の動作を行うことができない。右図のように環境から受け取った熱を電気エネルギーに変換すると熱力学第二法則に違反する。したがって負の静的抵抗は別に何らかのエネルギー源を必要とする。

通常の抵抗（静的抵抗 $R_{\text{static}}=v/i$ ）が負の値を取りうるかについてはいくらかの混乱がある。電子工学で「抵抗」という用語は慣例的に導線、抵抗器、ダイオードのような受動的な材料や素子にのみ用いられる。ジュールの法則 $P=i^{2}R_{\text{static}}$ が示すように、受動素子は負の静的抵抗を持つ（$R_{\text{static}}<0$）ことはできない。電力を消費する素子は符号規約により $P\geq 0$ であり、したがってジュールの法則から $R_{\text{static}}\geq 0$ となる。言い換えると、抵抗ゼロの「完全導体」よりよく電流を通す材料は存在しない。受動素子が負の静的抵抗を持つことはエネルギー保存則 もしくは熱力学第二法則（右図） に抵触する。このため、一部の著者は静的抵抗は負になりえないと述べている。

キルヒホッフの電圧則により、電池などの電源の静的抵抗（$R_{S}$）は常に負荷の静的抵抗（$R_{L}$）にマイナスをつけたものになる。

しかしながら、交流、直流を問わずいかなる電源においても端子電圧と電流の比 $v \over i$ が負になることは容易に示せる。素子が回路にエネルギーを送り出すには、電荷が素子中を電位が増加する向きに動く必要がある。このとき電流は負端子から正端子の向きに流れる。したがって電流は正端子から外に流れ出す。これは受動素子について決められた正電流とは逆向きなので、電流と電圧が逆符号となり、それらの比は負となる。

$R_{\mathrm {static} }={\frac {v}{i}}<0$

これはジュールの法則 から証明することもできる。

$P=iv=i^{2}R_{\mathrm {static} }$

上式によれば電力が素子から回路に向けて与えられる ($P<0$) のは $R_{\text{static}}<0$ の場合だけである。この量が負である場合に「抵抗」と呼べるかは慣習の問題となる。電源の静的抵抗は負となるが、どちらかというと仮想的な量であってあまり有用ではなく、正の抵抗と同じ意味で「抵抗」と見なすべきではない。たとえばこの量は負荷によって変わり、エネルギー保存の要請により回路の負荷抵抗（図の$R_{L}$）に単純にマイナスを付けたものと常に等しくなる。

電荷が素子中を電場に逆らって正端子に向けて動くには何らかのエネルギー源から仕事を受ける必要があり、エネルギー保存のため負性静的抵抗は電力源を備えていなければならない。電池や発電機のようなエネルギー変換機器を内部に備えていてもいいし、トランジスタ・真空管・オペアンプのような増幅器で行われているように外部電源と別に接続されていてもいい。

”Eventual passivity”（端部の受動性）

回路は無限の電圧・電流範囲にわたって負の静的抵抗を持つ（能動素子である）ことはできない。それには無限の電力が必要になってしまう。有限の電力しか持たない能動回路や素子はどこかで必ず受動的となる。つまり、向きはどうあれ十分に大きい電圧もしくは電流が加えられると静的抵抗が正となり電力を消費し始める。

したがって、原点から遠ざかるにつれて I–V 曲線は右上がりに変わり、第1・第3象限に入る。このため曲線が負の静的抵抗を持つのは原点付近に限定される。たとえば発電機や電池に開放電圧より高い電圧を加えると、電流の方向が逆になり、静的抵抗が正になって電力を消費するようになる。同じように、後述の負性インピーダンス変換器に対して電源電圧 $V_{s}$ より大きい電圧を加えると増幅器が飽和し、抵抗も正になる。

負性微分抵抗

負性微分抵抗を持つ素子または回路では、I–V 曲線の一部において電圧が増加するにつれて電流が減少する。

$r_{\mathrm {diff} }={\frac {dv}{di}}<0$

I–V 曲線は非単調（山と谷を持つ）となり、負の勾配を持つ領域が負性微分抵抗に当たる。

負性微分抵抗

電圧制御型（N型）。

電流制御型（S型）。

受動的な負性微分抵抗は静的抵抗が正であり、正味の電力を消費する。したがって I–V 曲線が通るのはグラフの第1象限と第3象限に限られ、原点を横切る。この条件があることから（ある種の漸近的なケースを除いて）負性抵抗領域は有限であり、正抵抗領域に挟まれており、原点を含まないと言える。

分類

負性微分抵抗は以下の2種類に分けられる（右図参照）。

• 電圧制御型（VCNR、短絡安定型、N型）このタイプでは電流は電圧の一価連続関数、電圧は電流の多価関数となる。ごく一般的なものは負性抵抗領域を1つしか持たず、全体的な曲線形はN字形となる。原点付近から電圧を上げていくと電流は増加して最大値 $i_{1}$ に達し、負性抵抗領域に入ると低下していって最小値 $i_{2}$ に至り、その後再び増加する。このタイプの負性抵抗を持つデバイスにはトンネルダイオード、共鳴トンネルダイオード、ラムダダイオード、ガンダイオード、ダイナトロン発振器がある。

• 電流制御型（CCNR、開放安定型、S型）電圧制御型とは双対の関係にあり、電圧は電流の一価関数、電流は電圧の多価関数となる。一般的なものは負性抵抗領域は一つしか持たず、曲線形はS字形である。このタイプの負性抵抗を持つ素子にはIMPATTダイオード、ユニジャンクショントランジスタ、SCR（シリコン制御整流子）をはじめとするサイリスタ、アーク放電、気体放電管がある。

複数の負性抵抗領域を持つデバイスも作成されている。安定状態を3つ以上持つデバイスもあり、多値論理を実装したデジタル回路での利用に関心が持たれている。

デバイス間比較に用いられる固有パラメータとして、負性抵抗領域の上端電流 $i_{1}$ と下端電流 $i_{2}$ の比であるPVR (peak-to-valley ratio) がある。

${\text{PVR}}=i_{1}/i_{2}$

この比が大きいほど、与えられた直流バイアス電流から取り出せる交流出力が大きくなり効率が向上する。

増幅

トンネルダイオード増幅回路。$r>R$ であるため二つの直列抵抗の和 ($R-r$) は負となり、入力電圧が増えると電流は減少する。回路の動作点はダイオードの特性曲線（黒）と抵抗器の負荷線（青）の交点である。入力電圧のわずかな増加 $v_{i}$（緑）によって負荷線が右にシフトすると、ダイオードを通る電流が大きく減少し、それによってダイオード両端の電圧 $v_{o}$ が大きく増加する。

負性微分抵抗デバイスが直流バイアスを受けて I–V 曲線の負性抵抗領域にあるときには、印加された交流信号を増幅できる。

右図のトンネルダイオード回路はその一例である。トンネルダイオードTDは電圧制御型の負性微分抵抗を持つ。電池 $V_{\text{b}}$ はダイオードの両端に一定のバイアス電圧をかけ、負性抵抗領域で動作させるとともに信号増幅に必要な電力を供給する。バイアス点での負性抵抗を $\Delta v/\Delta i=-r$ とする。安定性のためには $R$ が $r$ より小さくなければならない。分圧の式を用いると交流出力電圧は以下で与えられる。

$v_{\text{o}}={\frac {-r}{R-r}}v_{\text{i}}={\frac {r}{r-R}}v_{\text{i}}$

したがって電圧ゲインは

$G_{v}={\frac {r}{r-R}}$

通常の分圧器では、個々の枝の抵抗が全体の抵抗よりも小さいため出力電圧は入力よりも小さくなる。しかしここでは負性抵抗のため全交流抵抗 $r-R$ がダイオード単独の $r$ より小さく、そのため交流出力電圧 $v_{\text{o}}$ は入力 $v_{\text{i}}$ より大きくなる。電圧利得 $G_{v}$は1を超え、$R$ が $r$ に近づくにつれて際限なく上昇する。

パワーゲインの説明

バイアスした負性微分抵抗に交流電圧をかける様子。電流変化と電圧変化は逆符号（図では色で区別される）であるため、交流電力消費 $\Delta v\Delta i$ は負となり、素子は交流電力を生成する。

外部回路に接続した負性微分抵抗の交流等価回路。負性抵抗は入力に依存する交流電流源のように機能する。出力は $\Delta i=\Delta v/r$ となる。出力電流と電圧は逆位相であるため、正の交流電圧 $\Delta v$ に対して 交流電流の瞬時値 $\Delta i$ は端子から外に向けて流れる。これが負荷$R$ を通る交流電源電流 $\Delta i_{\text{S}}$ に加算されることで出力電力が増加する。

適切なバイアスを受けた負性微分抵抗素子が、端子を二つしか持たないにもかかわらず信号の電力を増幅しうる理由を右図に示す。重ね合わせの原理により、端子間電圧 $v(t)$ と電流 $i(t)$ は直流バイアス成分 （$V_{\text{bias}},I_{\text{bias}}$）と交流成分（$\Delta v,\Delta i$）に分けることができる。

$v(t)=V_{\text{bias}}+\Delta v(t)$

$i(t)=I_{\text{bias}}+\Delta i(t)$

正の電圧変化 $\Delta v$ が加わると負の電流変化 $\Delta i$ が生じるため、交流電流と交流電圧は位相が180°ずれる。すなわち、交流等価回路（図右）において交流電流の瞬時値 $\Delta i$ は素子中を交流電位 $\Delta v$ が増える向きに流れる。これは発電機と同じ振る舞いである。したがって交流消費電力は負であり、素子が交流電力を生み出して外部回路に向けて与える。

$P_{\text{AC}}=\Delta v\Delta i=r_{\text{diff}}|\Delta i|^{2}<0$

適切な外部回路を用いると、この素子は負荷が受ける交流信号の電力を増加させて増幅器として動作したり、共振回路に発振を励起して発振器として動作することができる。トランジスタやオペアンプのような2ポート増幅器とは異なり、増幅された信号は入力信号が印加されるのと同じ端子対から発する。

受動素子が生み出す交流電力は入力する直流バイアス電流から取られる。素子は直流電力を吸収し、その一部が素子の非線形性によって交流電力に変換され、印加信号を増幅する。したがって出力電力はバイアス電力によって制限される。

$|P_{\text{AC}}|\leq I_{\text{bias}}V_{\text{bias}}$

IV 平面の原点は負性微分抵抗領域に含まれない。さもなければ直流バイアス電流を流さずに信号増幅を行うことで電力入力なしに交流電力を生成できてしまう。素子中でも熱の散逸は存在し、その量は直流電力入力と交流電力出力の差に等しい。

素子にリアクタンスが存在する場合には電流と電圧の位相差はちょうど180°にはならず、周波数によって変わりうる。インピーダンスの実部が負（位相角が90~270°）である限り 素子は負性抵抗を持ち増幅を行える。

交流出力電力の最大値は負性抵抗領域（上のグラフにおける $v_{1},v_{2},i_{1},i_{2}$）のサイズによって決まる。

$P_{\text{AC(rms)}}\leq {\frac {1}{8}}(v_{2}-v_{1})(i_{1}-i_{2})$

反射係数

負性抵抗回路の一般（交流）モデル。負性微分抵抗素子$Z_{\text{N}}(j\omega )$ が外部回路 $Z_{\text{L}}(j\omega )$ に接続されている。外部回路の抵抗は正（$R_{\text{L}}>0$）である。素子、外部回路ともにリアクタンスを持ちうる（それぞれ$X_{\text{L}},X_{\text{N}}$）。

負性抵抗が入力信号と同じポートから信号を出力できる理由は、伝送線路理論によると端子対における交流電圧・電流は互いに逆向きに進む二つの波に分割できるためである。波の一つは素子に向かって進む入射波 $V_{\text{I}}$、もう一つは素子から遠ざかる反射波 $V_{\text{R}}$ である。回路の負性微分抵抗が増幅を行えるのは、入射波に対する反射波の比である反射係数 $\Gamma$ が1より大きい場合である。

$|\Gamma |\equiv {\bigg |}{\frac {V_{\text{R}}}{V_{\text{I}}}}{\bigg |}>1$

ただしここで

$\Gamma \equiv {\frac {Z_{\text{N}}-Z_{\text{L}}}{Z_{\text{N}}+Z_{\text{L}}}}$

負性微分抵抗素子の「反射信号」（出力）は入射信号より振幅が大きくなる。つまり「反射ゲイン」を持つ。反射係数は負性抵抗素子の交流インピーダンス$Z_{\text{N}}(j\omega )=R_{\text{N}}+jX_{\text{N}}$、および接続されている回路のインピーダンス $Z_{\text{L}}(j\omega )=R_{\text{L}}+jX_{\text{L}}$ によって決まる。$R_{\text{N}}<0$ かつ $R_{\text{L}}>0$ ならば $|\Gamma |>0$ であり、素子は増幅を行う。高周波回路の設計で補助図として広く使われているスミスチャートで負性微分抵抗を表すと、オーソドックスなチャートの外縁となる単位円 $|\Gamma |=1$のさらに外に当たる。そのため特殊な「拡張」チャートが必要になる。

安定条件

負性微分抵抗を持つ回路は非線形であり、I–V 曲線上に平衡点（直流で動作が可能な点）を複数持つことができる。平衡点において回路の極がすべてs平面の左半平面にあるならその点は安定であり、近傍から動作を始めるとそこに収束する。しかし極が虚数軸上にあるなら回路は振動し、右半平面にあるなら別の点に収束する。線形回路であれば平衡点は（安定であれ不安定であれ）ただ一つである。平衡点は直流バイアス回路によって決まり、その安定性は接続した回路の交流インピーダンス $Z_{\text{L}}(j\omega )$ で決まる。ただし、電圧制御型と電流制御型の負性抵抗では特性曲線の形が異なるため安定性条件も異なる。

• 電流制御型（S型）負性抵抗では抵抗 $R_{\text{N}}$ が一価関数である。したがって安定性は回路のインピーダンス方程式 $Z_{\text{L}}(j\omega )+Z_{\text{N}}(j\omega )=0$ の極によって決まる。

非リアクタンス性の回路の場合（$X_{\text{L}}=X_{\text{N}}=0$）、総抵抗が正であることが安定性の十分条件となる。

$Z_{\text{L}}+Z_{\text{N}}=R_{\text{L}}+R_{\text{N}}=R_{\text{L}}-r>0$

したがって電流制御型は以下のとき安定である。

$R_{\text{L}}>r$

電流制御型の負性抵抗は負荷抵抗を接続しない場合に（$R_{\text{L}}=\infty$）安定なため、「開放安定」と呼ばれる。

• 電圧制御型（N型）負性抵抗では、コンダクタンス $G_{\text{N}}=1/R_{\text{N}}$ が一価関数である。したがって安定性はアドミタンス方程式 $Y_{\text{L}}(j\omega )+Y_{\text{N}}(j\omega )=0$ によって決まる。このため電圧制御型負性抵抗は負性コンダクタンスとも呼ばれる。

先ほどと同様、非リアクタンス性の回路では総コンダクタンスが正となることが安定性の十分条件となる。

$Y_{\text{L}}+Y_{\text{N}}=G_{\text{L}}+G_{\text{N}}={1 \over R_{\text{L}}}+{1 \over R_{\text{N}}}={1 \over R_{\text{L}}}+{1 \over -r}>0$

${1 \over R_{\text{L}}}>{1 \over r}$

したがって電圧制御型負性抵抗は次の時に安定である。

$R_{\text{L}}<r$

上式は出力を短絡させたときにも（$R_{\text{L}}=0$）安定なため、電圧制御型負性抵抗は「短絡安定」と呼ばれる。

リアクタンスがゼロではない一般の負性抵抗回路についてはナイキストの安定条件のような標準的な方法で安定性を決定する必要がある。あるいは高周波の回路設計では、回路が安定する $Z_{\text{L}}(j\omega )$ の値はスミスチャートの「安定円」を用いた図法で決められる。

動作領域と用途

$R_{\text{N}}=-r$ かつ $X_{\text{N}}=0$ の単純な非リアクタンス性負性抵抗素子では、I–V 曲線に重ねた負荷線によって様々な動作領域を表すことができる（右図）。

電圧制御型（N型）の負荷線と安定領域。

電流制御型（S型）の負荷線と安定領域。

直流負荷線（図のDCL）とは直流バイアス回路によって決まる直線で、以下の式で表される。

$V=V_{\text{S}}-IR$

ここで $V_{\text{S}}$ は供給される直流バイアス電圧、$R$ は電源抵抗である。直流負荷線がI–V 曲線と交差する場所が直流動作点（Q点）となりうるが、安定性のためには以下の条件を満たす必要がある。

• 電圧制御型では低インピーダンスバイアス ($R<r$) が必要。電圧源など。
• 電流制御型では高インピーダンスバイアス ($R>r$) が必要。電流源、あるいは高い抵抗と電圧源を直列に接続するなど。

交流負荷線（図の L₁ ~ L₃）とは、Q点を通り、負荷回路の微分抵抗 $R_{\text{L}}$を傾きとする直線である。$R_{\text{L}}$を増加させると負荷線は反時計回りに回転する。回路の動作領域は $R_{\text{L}}$の値によって次の三つに分けられる（図参照）。

• 安定領域（緑）（図の L₁）この領域にある負荷線は1点 Q₁で I–V 曲線と交わる。非リアクタンス性回路においてこの領域は安定平衡（極が左半平面）であり、回路は安定する。負性抵抗増幅器はこの領域で駆動される。ただし、コンデンサやインダクタのようなエネルギー貯蔵素子を備えた回路はヒステリシスによって不安定になり、非線形弛張発振器（非安定マルチバイブレータ）または単安定マルチバイブレータとして動作する可能性がある。
  • 電圧制御型負性抵抗は $R_{L}<r$ で安定。
  • 電流制御型負性抵抗は $R_{L}>r$ で安定。
• 不安定点（図の L₂ ）$R_{L}=r$ のとき負荷線は I–V 曲線に接する。全微分抵抗がゼロ（極が複素平面の虚軸上）であるため回路は不安定であり、同調回路を接続していれば発振が起きる。線形発振器はこの点で駆動される。実用上の発振器は不安定領域で動作を始めるが、振幅が増大するにつれて振動の非線形性が増す。負性抵抗領域は有限であるため負性抵抗 r は振幅とともに減少していき、$r=R_{\text{L}}$ となったところで振幅が安定する。
• 双安定領域（赤）（図の L₃ ）この領域では負荷線は I–V 曲線と三つの点で交わることができる。中央の点 Q₁ は不安定平衡（極が右半平面）だが外側の二点 Q₂ 、Q₃ は安定平衡である。このためバイアスが適切なら回路は双安定であり、時間とともに Q₂ と Q₃ のいずれかに収束した後、入力パルスによって二点間を飛び移ることができる。フリップフロップ（双安定マルチバイブレータ）やシュミットトリガのようなスイッチング回路はこの領域で駆動される。
  • 電圧制御型負性抵抗は $R_{L}>r$ で双安定になる可能性がある。
  • 電流制御型負性抵抗は $R_{L}<r$ で双安定になる可能性がある。

能動抵抗

フィードバック増幅器で発生する能動負性抵抗の典型的な I–V 曲線。左図はN型、中図はS型に当たる。それぞれ負性抵抗領域（赤部分）を持っており、電力（灰色）を発生させる。ポートに十分な大きさの電圧か電流（向きは問わない）を加えると素子は非線形領域に入り、増幅器の飽和によって微分抵抗は正となる（曲線が黒い領域）。電力を発生させられる上限の印加電圧 $\pm V_{\text{S}}$ を超えると性的抵抗は正となり、素子は電力を消費し始める。負性抵抗はループゲイン$A\beta$ に依存する（図右）

ここまでに述べた受動素子はそれ自体が負性微分抵抗を持つが、回路にトランジスタやオペアンプのような増幅素子を組み込むことでポートの抵抗を負にすることもできる。増幅器に十分に強い正フィードバックを加えると入力インピーダンスや出力インピーダンスが負になりうる。フィードバックをかけていないときの増幅器の入力抵抗を $R_{\text{i}}$、増幅器のゲインを $A$、フィードバック経路の伝達関数を $\beta (j\omega )$とすると、正の並列フィードバックを用いたときの入力抵抗は以下となる。

$R_{\text{if}}={\frac {R_{\text{i}}}{1-A\beta }}$

したがってループゲイン$A\beta$ が1より大きいとき $R_{\text{if}}$は負になる。原点付近の I–V 曲線は原点を通る負勾配の直線であり（図参照）、ある動作範囲において「負の線形抵抗」 となる。微分抵抗と静的抵抗はいずれも負である。

${\Delta v \over \Delta i}={v \over i}=R_{\text{if}}<0$

そのため、線形動作範囲ではオームの法則によって負の抵抗 $-R$ を持つかのようにふるまう（このような増幅器は原点を通らない複雑な負性抵抗曲線を持つこともある）。

これらは回路理論において「能動抵抗」と呼ばれる。端子間に電圧を印加するとそれに比例する電流が（通常の抵抗とは逆に）正端子から流れ出す。たとえば端子に電池を接続すると、放電する代わりに充電される。

このような回路を1ポート素子と見なすと前述の受動負性微分抵抗素子と動作が似ており、やはり1ポート増幅器や発振器として利用できる。能動抵抗の使用には次のような利点がある。

• 能動素子であるため外部直流バイアスによる電力供給を必要とせず、DC結合で用いることができる。
• ループゲインの調節によって負性抵抗の値を変えられる。
• 線形回路素子として動作する。I–V 曲線の原点近傍の直線部分だけで動作させるなら電圧と電流が比例するため、高調波歪みが発生しない。

フィードバックループを並列と直列のどちらで接続するかによって電圧制御型（N型）と電流制御型（S型）の負性抵抗を選ぶこともできる。

フィードバック回路を用いれば負性リアクタンス（後述）を作ることもできるので、負の値を持つ能動線形回路素子として抵抗・コンデンサ・インダクタのいずれも実現できる。正の回路素子では不可能な伝達関数を作れることからアクティブフィルタで広く利用されている。このタイプの負性抵抗を利用している回路の例には負性インピーダンス変換器（NIC）、ジャイレータ、Deboo積分器、周波数依存負性抵抗（FDNR）、一般化イミタンス変換器（GIC）がある。

フィードバック発振器

このような正帰還増幅器の入力にLC回路を接続すると、入力側の負性微分抵抗 $R_{\text{if}}$ によってLC回路に内在する正の損失抵抗 $r_{\text{loss}}$ を打ち消すことができる。ちょうど $R_{\text{if}}=-r_{\text{loss}}$ ならば実質的に交流抵抗ゼロ（極が虚数軸上）のLC回路となる。このときLC回路は共振周波数で自発的に発振する。電力は増幅器から供給される。ハートレー発振器やコルピッツ発振器のようなフィードバック発振器はこのように動作する。負性抵抗モデルはフィードバック発振器の動作を理解する一つの方法である。線形発振回路は例外なく負性抵抗を持つが、フィードバック発振器はLC回路がフィードバックネットワークの不可欠な要素であることがほとんどなので、共振周波数の近傍でしか負性抵抗を持たない。

Q値の向上

同調回路の寄生損失抵抗を負性抵抗が完全には打ち消せない場合には（ $|R_{\text{if}}|<r_{\text{loss}}$ ）発振は起きないが、負性抵抗により減衰比が減少し（極が虚軸に向けて動く）Q値の向上を招くため、帯域幅は狭く、周波数選択性は高くなる。Q値の向上は「再生」とも呼ばれており、エドウィン・アームストロングが1912年に発明した再生無線受信機で初めて使用された。後には「Q増倍器」に用いられた。この手法はアクティブフィルタで広く使用されている。たとえば、RF集積回路はスペースを節約するためチップ上にらせん状に形成した導体からなる集積インダクタを用いる。この素子は損失が大きくQ値が低いため、高Q値同調回路を作成するときは負性抵抗と組み合わせる。

カオス回路

カオス的な振る舞いを示す回路は準周期的もしくは非周期的な発振器と見なせるため、一般の発振器と同様に電力供給用の負性抵抗を組み込む必要がある。単純な非線形回路でカオス系の典型例として広く使われているチュア回路の場合、チュア・ダイオードなどと呼ばれる非線形能動抵抗素子を必要とする。通常これは負性インピーダンス変換回路を用いて構成される。

負性インピーダンス変換器

負性インピーダンス変換器（左）と I–V 曲線（右）。曲線の赤い領域で負性微分抵抗を持ち、灰色の領域で電力を発生できる。

よく知られた能動抵抗回路に、図に示す負性インピーダンス変換器（NIC）がある。抵抗器 $R_{\text{1}}$ 二つとオペアンプにより構成されたゲイン2の負帰還非反転増幅器である。オペアンプの出力電圧は以下で与えられる。

$v_{\text{o}}={\frac {v(R_{1}+R_{1})}{R_{1}}}=2v$

そのため入力に電圧 $v$を印加すると同じ電圧が $Z$ の両端に逆向きに加わり、そこに流れた電流が入力から出ていく。電流の値は

$i={\frac {v-v_{\text{o}}}{Z}}={\frac {v-2v}{Z}}=-{\frac {v}{Z}}$

であり、したがって回路の入力インピーダンスは以下となる。

$z_{\text{in}}={\frac {v}{i}}=-Z\,$

こうしてインピーダンス $Z$ が $-Z$ に変換される。$Z$ が抵抗 $R$ の抵抗器であれば、オペアンプの線形動作範囲 $V_{\text{S}}/2<v<-V_{\text{S}}/2$ 内で入力インピーダンスは $-R$ の線形「負性抵抗器」としてふるまうことになる。この入力ポートを一つの素子であるかのように扱って別の回路に組み込む。負性インピーダンス変換器を用いると回路の不要な正抵抗を打ち消すことができる。たとえば、最初に開発されたのは電話線の抵抗を打ち消して中継器として機能させるためだった。

負の静電容量とインダクタンス

前述の回路の $Z$ をコンデンサ ($C$) もしくはインダクタ ($L$) で置き換えれば負の静電容量やインダクタンスを作ることもできる。負の静電容量の I–V 特性、およびインピーダンス $Z_{\text{C}}(j\omega )$ は以下のように表される。

$i=-C{dv \over dt}\qquad \qquad Z_{C}=-{\frac {1}{j\omega C}}$

ただし $C>0$ である。負性静電容量に正の電流を流すと放電が起き、電圧が低下する。同様に負性インダクタンスの I–V 特性とインピーダンス $Z_{L}(j\omega )$ は以下である。

$v=-L{di \over dt}\qquad \qquad Z_{L}=-j\omega L$

負の静電容量またはインダクタンスは回路の不要な正の静電容量やインダクタンスを打ち消すために用いられる。負性インピーダンス変換回路は電話線のリアクタンスを打ち消すために用いられた。

別の観点から見ると、負性静電容量を流れる電流は正の静電容量の場合とは位相が180°反転しており、電流が電圧より90°先行する代わりにインダクタンスと同じく90°遅延する。したがって負性静電容量は、インピーダンスの周波数依存性が通常とは逆のインダクタンスであるかのように動作する。実際のインダクタンスであれば周波数 ω とともにインピーダンスが増加するが、負性静電容量では減少するのである。同様に負性インダクタンスは周波数とともにインピーダンスが増加する静電容量であるかのように動作する。負性静電容量と負性インダクタンスはフォスターのリアクタンス定理に反する「非フォスター的」回路である。研究段階の応用の一つに、現在の整合回路網のように単一の周波数だけでなく、広範囲の周波数にわたってアンテナと伝送線路をマッチングできる動的整合回路網がある。これによりチュー＝ハリントンの限界を超えた広い帯域幅を持つ小型のアンテナを作成できると考えられる。

発振器

空洞共振器と内部のガンダイオードからなる発振器。ダイオードの負性抵抗により空洞内にマイクロ波振動が励起され、開口部から導波管（写真には写っていない）へと放射される。

負性微分抵抗素子は電子発振器の部品として広く用いられている。負性抵抗発振器ではIPMATTダイオード、ガンダイオード、マイクロ波真空管のような負性微分抵抗素子がLC回路、水晶振動子、誘電体共振器、空洞共振器のような電気共振器の両端に接続されており、さらに素子を負性抵抗領域にバイアスするとともに電力を供給するための直流電源を備えている。LC回路のような共振器はほとんど発振器と差がなく、電気的な振動のエネルギーを蓄えることができる。しかし共振器には必ず内部抵抗などの損失があるため振動は減衰して消えてしまう。負性抵抗は正抵抗を打ち消すことで実質的に損失のない共振器を作り出す。そこでは共振器の共振周波数で自発的に連続的な振動が発生する。

用途

負性抵抗発振器はフィードバック発振器が十分に機能しないマイクロ波以上の高周波で主に使われる。マイクロ波ダイオードはスピードガンや衛星放送受信器の局部発振器用に用いられる低出力から中出力の発振器に組み込まれる。マイクロ波エネルギー源としての用途は広く、ミリ波 およびテラヘルツ波領域では事実上唯一の固体エネルギー源である。マグネトロンなどの負性抵抗マイクロ波真空管は出力がより高く、レーダー送信機や電子レンジのような用途に用いられる。ユニジャンクショントランジスタをネオン灯などの気体放電灯と組み合わせると、より低周波で動作する弛張発振器を作ることができる。

負性抵抗発振器のモデルはダイオードのような1ポート素子に限定されるものではなく、トランジスタや真空管のような2ポート素子に基づくフィードバック発振回路にも適用できる。また近年の高周波発振器では、トランジスタがダイオードのような1ポート負性抵抗デバイスとして使用されることが多くなってきている。マイクロ波周波数ではトランジスタの一方のポートにある負荷を与えると内部フィードバックによって不安定になり、もう一方のポートに負性抵抗を示すことがある。そこで高周波トランジスタ発振器の設計では、トランジスタのポートの一つにリアクタンス性の負荷を与えて負性抵抗を持たせ、もう一方のポートを共振器の両端に接続して負性抵抗発振器となるように設計する（以下参照）。

ガンダイオード発振器

ガンダイオード発振器の回路図。

交流等価回路。

ガンダイオード発振器の負荷線。
DCL: Q点を決める直流負荷線。
SSL: 起動時に振幅がまだ小さい間の負荷線。$r<R$ であるため極は右半平面にあり、振動の振幅は増加する。
LSL: 大信号での負荷線。交流電流の振幅が負性抵抗領域の端に近づくにつれて（緑）、正弦波のピークが歪み（クリッピング）、$r$ は減少していって$R$ と等しくなったところで安定する。

一般的なガンダイオード発振器（右上回路図参照）は 負性抵抗発振器の機能を示す好例である。ダイオード D は電圧制御型（N型）の負性抵抗を持っており、電圧源 $V_{\text{b}}$ のバイアスによって負性抵抗領域で動作している。微分抵抗は $dv/di\;=\;-r$ である。チョークコイル RFC は交流電流がバイアス電源へ流れ込むのを防ぐ。$R$ は直列同調回路 $LC$ で起きる損失の等価抵抗に任意の負荷抵抗を加算したものである。この交流回路にキルヒホッフの電圧則を適用すると、交流電流 $i(t)$ に関する以下の微分方程式が作れる。

${\frac {d^{2}i}{dt^{2}}}+{\frac {R-r}{L}}{\frac {di}{dt}}+{\frac {1}{LC}}i=0$

これを解いて以下の形の解を得る。

$i(t)=i_{0}e^{\alpha t}\cos(\omega t+\phi )$

ここで

$\alpha ={\frac {r-R}{2L}},\quad \omega ={\sqrt {{\frac {1}{LC}}-\left({\frac {r-R}{2L}}\right)^{2}}}$

である。

上式は回路を流れる電流 $i(t)$ が直流バイアス点 $I_{\text{bias}}$ の周りで時間変化することを示している。ゼロではない初期電流 $i(0)=i_{0}$ から開始すると電流はおおよそ同調回路の共振周波数 ω で正弦的に振動し、振幅は $\alpha$ 次第で一定となるか、または指数関数的に増加もしくは減少する。回路が一定の発振を維持できるかどうかは正抵抗 $R$ と負抵抗 $r$ のバランスによって決まる。

1. 

   $r<R\Rightarrow \alpha <0$ ：(極は左半平面）ダイオードの負性抵抗が同調回路の正抵抗よりも小さければ正の減衰が起きる。回路内で起きるあらゆる振動は抵抗器 $R$ の発熱でエネルギーを奪われ、単なる同調回路の場合と同じように指数関数的に弱まって消える。すなわち回路は発振しない。

2. 

   $r=R\Rightarrow \alpha =0$ :（極は虚軸上）正負の抵抗が等しい場合、正味の抵抗がゼロなので減衰はない。同調回路と負荷での損失をちょうど補償するだけのエネルギーをダイオードが供給するため、回路でいったん発振が始まると一定の振幅で継続する。発振器が定常的に動作している状態にあたる。

3. 

   $r>R\Rightarrow \alpha >0$ ：(極は右半平面）負性抵抗が正抵抗より大きい場合、減衰が負となるため、振動のエネルギーと振幅は指数関数的に増加する。発振器が起動している最中の状態である。

実用的な発振器は、発振を始めさせるため正味の抵抗を負として上記の領域 (3) で設計されている。経験則として $R=r/3$ とされることが多い。電源がオンになると、回路中の電気的ノイズが発振開始に必要な信号 $i_{0}$ を供給し、指数関数的に振動が成長していく。ただし無限に成長することはなく、振幅はやがてダイオードの非線形性によって制限される。

信号振幅が大きいと回路が非線形になるため、上述の線形解析は厳密には成り立たず、微分抵抗は不確定になる。しかし、1周期にわたる「平均」抵抗が $r$ だと考えれば理解は可能である。正弦波の振幅が負性抵抗領域の幅を超え、I–V 曲線の微分抵抗が正となる領域にまで電圧変動がはみ出すと、平均の負性微分抵抗 $r$ が小さくなって全抵抗 $R-r$ と減衰定数 $\alpha$ が負からゼロに近づき、最終的に正に転じる。したがって振動は減衰がゼロになる $r=R$ で安定する。

ガンダイオードの負性抵抗は −5〜−25 Ωの範囲である。$R$ が $r$ に近く、発振開始に最低限必要な程度である場合、電圧振幅は I–V 曲線の線形部分を大きく超えず、出力波形はほぼ正弦波となって周波数も非常に安定する。$R$ が $r$ よりはるかに小さい回路では I–V 曲線の非線形部分にまで振動が広がるため出力正弦波のクリッピング歪みが問題になり、周波数は電源電圧にますます依存するようになる。

回路の種類

負性抵抗発振回路には電圧制御型（VCNR）と電流制御型（CCNR）の二種類がある。

• 電圧制御型負性抵抗発振器： 電圧制御型（N型）素子は低インピーダンスのバイアスを必要とし、$r$ より小さい負荷インピーダンスに対して安定する。よって発振回路は右上図のように電圧源 $V_{\text{bias}}$ によって素子をバイアスし、負荷として並列共振回路を用いるのが理想になる。共振回路のインピーダンスはその共振周波数でのみ高くなるため、その周波数でのみ回路は不安定になり発振する。

• 電流制御型負性コンダクタンス発振器：対照的に、電流制御型（S型）素子は高インピーダンスのバイアスを必要とし、$r$ より大きい負荷インピーダンスに対して安定する。理想的な発振回路は右図のようにバイアスとして電流源 $I_{\text{bias}}$ を用い（電圧源を大きい抵抗と直列にして用いることもある）、直列共振回路を負荷とする。直列LC回路のインピーダンスは共振周波数でのみ低くなるため、その周波数だけで発振が起きる。

発振条件

ほとんどの発振器は能動素子と負荷の両者が抵抗（$R$）に加えてリアクタンス（$X$）を持ちうるため、ガンダイオードの例より複雑になる。現在の負性抵抗発振器は黒川兼行による周波数領域の手法を用いて設計される。回路図は仮想的な「基準面」（赤）によって能動素子を含む負性抵抗部分と共振回路と外部負荷からなる正抵抗部分に分割される。負性抵抗部分の複素インピーダンス

$Z_{\text{N}}=R_{\text{N}}(I,\omega )+jX_{\text{N}}(I,\omega )$

は周波数 ω に依存するだけでなく非線形でもあり、一般に交流発振電流 I の振幅が増えると減少する。一方、共振器部分のインピーダンス

$Z_{\text{L}}=R_{\text{L}}(\omega )+jX_{\text{L}}(\omega )$

は線形であり周波数にしか依存しない。回路方程式は

$(Z_{\text{N}}+Z_{\text{L}})I=0$

となるため、発振が起きる（非ゼロの I を持つ）のは $Z_{\text{N}}+Z_{\text{L}}$がゼロとなる周波数 $\omega$ と振幅 $I$ においてのみである。すなわち正負の抵抗の大きさが等しく、リアクタンスが複素共役でなければならない。

$R_{N}\leq -R_{L}$ かつ $X_{N}=-X_{L}$

定常的な発振が続いているときには上式の等号が成立する。起動時に発振を始めるには抵抗が負側に傾いていなければならないため、上式の不等号が成り立つ。

発振条件は反射係数を用いて表すこともできる。基準面での電圧波形は、負性抵抗素子に向かって伝播する成分 $V_{1}$ と、逆に共振器に向かって伝播する成分 $V_{2}$ に分けられる。能動素子の反射係数 $\Gamma _{\text{N}}=V_{2}/V_{1}$ は1より大きいが、共振器側の $\Gamma _{\text{L}}=V_{1}/V_{2}$ は1未満となる。動作中、波は両側で何度も反射されるため、回路が発振するのは以下の場合だけである。

$|\Gamma _{\text{N}}\Gamma _{\text{L}}|\geq 1$

先ほどと同様、上式の等号は定常的な発振の条件を与え、不等号は起動時に負性抵抗が過剰となるために要求される。この条件はフィードバック発振器でいうバルクハウゼンの安定条件にあたり、必要条件だが十分条件ではないため、上式を満たしても振動しない回路もある。黒川はより複雑な十分条件も導いており、そちらが代わりに用いられることも多い。

増幅器

ガンダイオードやIMPATTダイオードのような負性微分抵抗素子は増幅器（特にマイクロ波領域のもの）にも利用されるが、発振器ほど一般的ではない。トランジスタのような2ポート素子と異なり負性抵抗素子にはポートが1つしかないため、増幅された出力信号は入力と同じ端子から出ていく必要がある。何らかの方法で2つの信号を分離しなければ負性抵抗増幅器は二方向性となり、負荷インピーダンス依存性やフィードバックの発生が問題となる。多くの負性抵抗増幅器は入力信号と出力信号を分離するためにアイソレータや方向性結合器のような不可逆回路素子を使用している。

反射増幅器

反射増幅器の交流等価回路。

二つのトンネルダイオード反射増幅器をカスケード接続した、8-12 GHzで動作するマイクロ波増幅器。

広く使用されている回路の1つに、サーキュレータによって信号を分離する反射増幅器がある。サーキュレータは3つのポートを持つ不可逆固体回路素子で、あるポートに入射した信号を隣のポートの片方に送る。つまりポート1に入射した信号をポート2へ、ポート2からの信号をポート3へ、ポート3から1へと送る。右図に示す反射増幅器ではポート1に信号が入力され、ポート2にはバイアスを含む電圧制御型負性抵抗ダイオード N がフィルター F を介して接続されており、出力回路はポート3に置かれている。入力信号はポート1からポート2のダイオードに送られるが、ダイオードから「反射」された増幅信号はポート3に流されるため出力から入力への結合はほとんどない。入出力の伝送線路の特性インピーダンス $Z_{0}$（通常は50 Ω）はサーキュレータのポートとインピーダンス整合が取られている。フィルタ F は適切なインピーダンスを与えてダイオードのゲインを調節するためにある。高周波において負性抵抗ダイオードは純粋な抵抗性負荷ではなくリアクタンスを持つため、フィルタにはこれを共役リアクタンスで打ち消して定在波を防ぐ役割もある。

フィルタはリアクタンス成分しか持たずそれ自体では電力を吸収しないため、電力はダイオードとポートの間を無損失で通過する。ダイオードへ入力される信号の電力は

$P_{\text{in}}=V_{I}^{2}/R_{1}$

ダイオードからの出力電力は

$P_{\text{out}}=V_{R}^{2}/R_{1}$

したがって増幅器のパワーゲイン$G_{P}$ は反射係数の自乗で与えられる。

$G_{\text{P}}={P_{\text{out}} \over P_{\text{in}}}={V_{R}^{2} \over V_{I}^{2}}=|\Gamma |^{2}$

$|\Gamma |^{2}={\Bigg |}{Z_{\text{N}}-Z_{1} \over Z_{\text{N}}+Z_{1}}{\Bigg |}^{2}$

$|\Gamma |^{2}={\Bigg |}{R_{\text{N}}+jX_{\text{N}}-(R_{1}+jX_{1}) \over R_{\text{N}}+jX_{\text{N}}+R_{1}+jX_{1}}{\Bigg |}^{2}$

$R_{\text{N}}$ はダイオードの負性抵抗 $-r$ にあたる。フィルタとダイオードの整合が取れている、すなわち $X_{1}=-X_{\text{N}}$ だと仮定すると、ゲインは以下のようになる。

$G_{\text{P}}=|\Gamma |^{2}={(r+R_{1})^{2}+4X_{\text{N}}^{2} \over (r-R_{1})^{2}}$

ここまでに述べた電圧制御型反射増幅器は $R_{1}<r$ において安定する。電流制御型であれば安定条件は $R_{1}>r$ となる。上式によるとゲインに上限はなく、$R_{\text{1}}$ が振動点 $r$ に近づくにつれて無限大に発散する。これは負性抵抗増幅器に共通する特性であり、ゲインに上限があるが無条件で安定することが多い一般的な2ポート増幅器とは対照をなしている。ただし実地ではサーキュレータの逆方向ポート間にはたらく「リーク」結合によってゲインは制限される。

メーザーとパラメトリック増幅器は非常に低ノイズの負性抵抗増幅器であり、電波望遠鏡のような用途の反射増幅器に組み込まれている。

スイッチング回路

負性微分抵抗素子はスイッチング回路においても用いられ、ある状態から別の状態に敏速に変化するヒステリシス性を持った非線形素子として機能する。その利点は、弛張発振器やフリップフロップならびにメモリセルの機能を実現する標準的な論理回路である双安定マルチバイブレータには能動素子（トランジスタ）が二つ必要なのに対して、負性抵抗素子を用いれば単一の能動素子で済むところにある。スイッチング回路には3種類ある。

• 非安定マルチバイブレータ：二つの不安定な状態を持つ回路で、出力は状態間を周期的に移り変わる。片方の状態に留まる時間は付属するRC回路の時定数で決まる。すなわち弛張発振器の一種であり、方形波か三角波を発生することができる。
• 単安定マルチバイブレータ：不安定状態と安定状態を一つずつ持つ回路。安定状態にあるときにパルスが入力されると出力がもう一方の状態に切り替わり、RC回路の時定数に応じて一定時間その状態を維持してから安定状態に戻る。これによりタイマーもしくは遅れ要素として用いることができる。
• 双安定マルチバイブレータもしくはフリップフロップ：二つの安定状態を持つ回路。状態は入力パルスにより切り替わる。メモリ回路やデジタルカウンタとして用いることができる。

その他の例

ニューロンモデル

いくつかのニューロンが I–V 特性に負勾配コンダクタンス領域（RNSC）を持つことが電位固定法によって明らかにされている。RNSCは哺乳類の脊髄ニューロンにおけるリズミカルな運動パターンの形成に関与している可能性がある。

歴史

負性抵抗は19世紀に照明とされていたアーク放電の研究を通じて初めて認識された。Alfred Niaudetは1881年に アーク電流が増加するにつれてアーク電極間の電圧が一時的に低下することを見出したが、多くの研究者は温度による二次的な効果だとみなした。この効果に "negative resistance" という言葉を当てる者もいたが、受動素子が負の抵抗を持ちえないことはよく知られていたため異論も呼んだ。ハータ・エアトンは1895年から夫ウィリアムの研究を受け継いでアーク放電の I–V 曲線を綿密に測定し、負の勾配を持つ領域を発見して論争を引き起こした。フリスとロジャーズは1896年に エアトン夫婦の援助を受けて微分抵抗 $dv/di$ の概念を導入し、やがてアーク放電が負の微分抵抗を持つことが徐々に受け入れられていった。これらの研究が認められたハータ・エアトンは投票によって女性として初めて英国電気学会への入会が許された。

アーク送信機

1892年にジョージ・フィッツジェラルドは共振回路の減衰抵抗をゼロまたは負にすれば連続的な発振を起こせることに初めて気づいた。同年、エリフ・トムソンはLC回路をアーク電極に接続して負性抵抗発振器を作成した。おそらくこれが最初に作られた電子発振器である。ロンドン中央工科大学でウィリアム・エアトンの学生だったウィリアム・ダッデルはトムソンのアーク発振器に一般の関心を向けさせた。アークを流れる電流は負性抵抗のため不安定であり、そのためアーク灯はヒス音やハム音、さらにはハウリング音を立てるのが常だったが、この効果を研究していたダッデルは1899年にアークの両端にLC回路を接続し、負性抵抗により発振を起こして楽音を発生させてみせたのである。この発明のデモンストレーションでは複数の同調回路がアークにつながれて楽曲を演奏した。ダッデルの「シンギング・アーク」発振器は可聴周波数でしか動作しなかったが、1903年にデンマーク人のエンジニア、ヴォルデマール・ポールセンとＰ・Ｏ・ペダーソンが水素雰囲気中で磁場をかけた状態でアークを起こすことで周波数範囲をラジオ波にまで拡大してポールセン・アーク無線送信機を発明した。この装置は1920年代まで広く使用されていた。

真空管

20世紀初頭にはまだ負性抵抗の物理的原因は理解されていなかったが、工学者はそれを使えば発振を起こせることは知っており、応用を行い始めた。ハインリッヒ・バルクハウゼンは1907年に発振器が負性抵抗を持たなければならないことを示した。エルンスト・ルーマーとアドルフ・ピーパーは水銀灯が発振を起こせることを発見し、1912年にはAT＆Tがこれを利用して電話線用の増幅中継器を製造した。

1918年、ゼネラル・エレクトリックのアルバート・ハルは真空管が二次電子放出と呼ばれる現象により動作範囲の一部で負性抵抗を持ちうることを発見した。真空管中のプレート電極は正バイアスによって電子を引き寄せるが、電位が高すぎると加速された電子がプレート表面から別の電子をたたき出すことがある。これにより、条件によってはプレート電圧を増加させると実質的にプレート電流が減少する。ハルは真空管にLC回路を接続することでダイナトロンという一種の発振器を作成した。その後もジョン・スコット＝タガートによる1919年のバイオトロン やハルによる1920年のマグネトロンのように負性抵抗を利用した真空管発振器の発明が続いた。

負性インピーダンス変換機はマリウス・ラトゥールが1920年ごろに行った研究に端を発する。ラトゥールは負性静電容量と負性インダクタンスを最初に報告した一人でもある。その10年後、ベル研究所でジョージ・クリソンらによって負性インピーダンス変換器が電話線中継器として開発され、大陸横断通話実現の道を開いた。1953年にリンヴィルがいち早くトランジスタを導入したことで負性インピーダンス変換器への関心は高まり、新しい回路やアプリケーションが次々と開発されていった。

固体素子

半導体における負性微分抵抗は、1909年ごろにウィリアム・エクルズ やG・W・ピカード などによって最初の点接触型ダイオードである「ネコのひげ型」検波器で見つかっていた。エクルズらは無線検出器としての感度を向上させるために接合を直流電圧でバイアスすると自発的な発振が起きることに気づいていたが、この効果は深く追求されなかった。

負性抵抗ダイオードを実用に供した最初の人物はロシア人の無線研究者オレク・ロシェフである。ロシェフは1922年にバイアスをかけた紅亜鉛鉱（酸化亜鉛）の点接触接合が負性微分抵抗を持つことを見出し、これを利用して増幅器や発振器、また再生増幅機能を備えた無線受信機を固体デバイスで作成した。トランジスタが発明される25年前のことである。後にはスーパーヘテロダイン受信機を構築しさえした。しかしこれらの業績は真空管技術の興隆に覆い隠された。ロシェフは10年のうちに研究を放棄し、この技術（ヒューゴー・ガーンズバックによって「クリストダイン」と名付けられた）は忘れられた。

最初に広く使用されるようになった固体負性抵抗デバイスは、1957年に日本人の物理学者江崎玲劣奈が発明したトンネルダイオードである。この種のダイオードは接合サイズが小さいことから寄生容量が低く、そのためより高い周波数で動作し、通常の真空管発振器の限界を超えるマイクロ波周波数で電力を発生できるものだった。トンネルダイオードの登場によりマイクロ波発振器に用いるための負性抵抗半導体デバイスが探求され始め、IMPATTダイオード、ガンダイオード、TRAPATTダイオードなどが生み出されていった。1969年、黒川兼行は負性抵抗回路の安定性に関する条件を導出した。現在マイクロ波エネルギーの発生源としては負性微分抵抗ダイオード発振器が最も広く利用されており、ここ数十年でも多くの新しい負性抵抗素子が見つかっている。

参考文献

• Gottlieb, Irving M. (1997). Practical Oscillator Handbook. Elsevier. ISBN 978-0080539386. https://books.google.com/books?id=e_oZ69GAuxAC&q=%22negative+resistance&pg=PA75  ― 発振器での負性微分抵抗の動作を解説している（英語）。
• Hong, Sungook (2001). Wireless: From Marconi's Black-Box to the Audion. USA: MIT Press. ISBN 978-0262082983. http://monoskop.org/images/f/f4/Hong_Sungook_Wireless_From_Marconis_Black-Box_to_the_Audion.pdf , ch. 6 ― 負性抵抗の発見と初期の無線通信における役割についての記事（英語）。
• Snelgrove, Martin (2008). "Negative resistance circuits". AccessScience Online Encyclopedia. McGraw-Hill. 2012年5月17日閲覧。 ― 負性抵抗に関する1ページの初歩的な手引き（英語）。