三角関数

三角関数（さんかくかんすう、英: trigonometric function）とは、平面三角法における、角の大きさと線分の長さの関係を明らかにする関数の族および、それらを拡張して得られる関数の総称である。三角関数という呼び名は三角法に由来するもので、後述する単位円を用いた定義に由来する呼び名として、円関数（えんかんすう、英: circular function）と呼ばれることがある。定義域の違いを除けば両者は同じ関数を指し、あるいは単に三角関数と呼ぶ場合も、円関数のように何らかの意味で拡張された三角関数を指すことが多い。

三角関数には sin, sec, tan, cos, csc, cot の 6 つがあり、それぞれ正弦 (sine)、正割 (secant)、正接 (tangent)、余弦 (cosine)、余割 (cosecant)、余接(cotangent) を意味する。特に sin, cos は幾何学的にも解析学的にも単純な良い性質を持っているので、様々な分野で用いられる。例えば波や電気信号などは正弦関数と余弦関数を組み合わせることで表現することができる。この事実はフーリエ級数およびフーリエ変換の理論として知られ、音声などの信号の合成や解析の手段として利用されている。他にもベクトルの外積や内積は正弦関数および余弦関数を用いて表すことができ、ベクトルを図形に対応づけることができる。

三角関数に用いられる独特な記法として、三角関数の累乗と逆関数に関するものがある。通常、関数 f (x) の累乗は (f (x))² や (f (x))⁻¹ のように書くが、三角関数の累乗は sin²x のように書かれることが多い。逆関数については通常の記法と同じく、sin⁻¹x などと表すことが多い（この文脈では従って、三角関数の逆数は分数を用いて 1/sin x のように表される）。文献あるいは著者によっては、通常の記法と三角関数に対する特殊な記法との混同を避けるため、三角関数の累乗を通常の関数と同様にするか、三角関数の逆関数として −1 と添え字する代わりに関数の頭に arc とつけることがある（たとえば sin の逆関数として sin⁻¹ の代わりに arcsin を用いる）。

定義

直角三角形による定義

∠C を直角とする直角三角形ABC

直角三角形において、1 つの鋭角の大きさが決まれば、三角形の内角の和は 180°であることから他の 1 つの鋭角の大きさも決まり、3 辺の比も決まる。ゆえに、角度に対して辺比の値を与える関数を考えることができる。

∠C を直角とする直角三角形 ABC において、それぞれの辺の長さを AB = h, BC = a, CA = b と表す（図を参照）。∠A = θ に対して三角形の辺の比 h : a : b が決まることから、

${\begin{aligned}&{\begin{cases}\sin \theta ={\frac {a}{h}}\\\sec \theta ={\frac {h}{b}}={\frac {1}{\cos \theta }}\\\tan \theta ={\frac {a}{b}}={\frac {\sin \theta }{\cos \theta }}\end{cases}}\\&{\begin{cases}\cos \theta ={\frac {b}{h}}\\\operatorname {cosec} \theta =\csc \theta ={\frac {h}{a}}={\frac {1}{\sin \theta }}\\\cot \theta ={\frac {b}{a}}={\frac {1}{\tan \theta }}\end{cases}}\end{aligned}}$

という 6 つの値が定まる。それぞれ正弦（sine; サイン）、正割（secant; セカント）、正接（tangent; タンジェント）、余弦（cosine; コサイン）、余割（cosecant; コセカント）、余接（cotangent; コタンジェント）と呼び、まとめて三角比と呼ばれる。ただし cosec は長いので csc と略記することも多い。ある角 ∠A に対する余弦、余割、余接はその角 ∠A の余角 (co-angle) に対する正弦、正割、正接として定義される。

${\begin{cases}\cos \theta =\sin \left(90^{\circ }-\theta \right)=\sin \left({\frac {\pi }{2}}-\theta \right)\\\csc \theta =\sec \left(90^{\circ }-\theta \right)=\sec \left({\frac {\pi }{2}}-\theta \right)\\\cot \theta =\tan \left(90^{\circ }-\theta \right)=\tan \left({\frac {\pi }{2}}-\theta \right)\end{cases}}$

三角比は平面三角法に用いられ、巨大な物の大きさや遠方までの距離を計算する際の便利な道具となる。角度 θ の単位は、通常度またはラジアンである。

三角比、すなわち三角関数の直角三角形を用いた定義は、直角三角形の鋭角に対して定義されるため、その定義域は θ が 0° から 90° まで(0 から π/2 まで)の範囲に限られる。また、θ = 90° (= π/2) の場合 sec, tan が、θ = 0°(= 0) の場合 csc, cot がそれぞれ定義されない。これは分母となる辺の比の大きさが 0 になるためゼロ除算が発生し、その除算自体が数学的に定義されないからである。一般の角度に対する三角関数を得るためには、三角関数について成り立つ何らかの定理を指針として、定義の拡張を行う必要がある。後述する単位円による定義は初等幾何学におけるそのような拡張の例である。他に同等な方法として、正弦定理や余弦定理を用いる方法などがある。

単位円による定義

単位円による、6つの三角関数が表す長さ

2 次元ユークリッド空間 R² における単位円 {x(t)}² + {y(t)}² = 1 上の点を A = (x(t), y(t)) とする。反時計回りを正の向きとして、原点と円周を結ぶ線分 OA と x 軸のなす角の大きさ ∠xOA を媒介変数 t として選ぶ。このとき実変数 t に対する三角関数は以下のように定義される。

${\begin{aligned}\sin t&=y\\\cos t&=x\\\tan t&={\frac {y}{x}}={\frac {\sin t}{\cos t}}\end{aligned}}$

これらは順に正弦関数 (sine function)、余弦関数 (cosine function)、正接関数(tangent function) と呼ばれる。さらにこれらの逆数として以下の 3 つの関数が定義される。

${\begin{aligned}\csc t&={\frac {1}{y}}={\frac {1}{\sin t}}\\\sec t&={\frac {1}{x}}={\frac {1}{\cos t}}\\\cot t&={\frac {x}{y}}={\frac {1}{\tan t}}\end{aligned}}$

これらは順に余割関数 (cosecant function)、正割関数 (secant function)、余接関数 (cotangent function) と呼ばれ、sin, cos, tan と合わせて三角関数と総称される。特に csc, sec, cot は割三角関数（かつさんかくかんすう）と呼ばれることがある。

この定義は 0 < t < π/2 の範囲では直角三角形による定義と一致する。

級数による定義

角度、辺の長さといった幾何学的な概念への依存を避けるため、また定義域を複素数に拡張するために、級数を用いて定義することもできる。この定義は実数の範囲では単位円による定義と一致する。以下の級数は共に示される収束円内で収束する。

• z を複素変数、B_n をベルヌーイ数、E_n をオイラー数とする。

${\begin{aligned}\sin z&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}\quad {\text{for all}}\ z,\\\cos z&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}\quad {\text{for all}}\ z,\\\tan z&=\sum _{n=1}^{\infty }{\frac {(-1)^{n}2^{2n}(1-2^{2n})B_{2n}}{(2n)!}}z^{2n-1}\quad {\text{for}}\ |z|<{\frac {\pi }{2}},\\\cot z&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}}{(2n)!}}z^{2n-1}\quad {\text{for}}\ 0<|z|<\pi ,\\\sec z&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}z^{2n}\quad {\text{for}}\ |z|<{\frac {\pi }{2}},\\\csc z&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2-2^{2n})B_{2n}}{(2n)!}}z^{2n-1}\quad {\text{for}}\ 0<|z|<\pi .\end{aligned}}$

微分方程式による定義

三角関数は以下に示す実変数 x に対する実関数 y(x) の 2 階の常微分方程式の解としても定義できる。

$y''(x)=-y(x).$

(1)

(1) を 1 階の連立常微分方程式に書き換えると、y(x) = f (x), y'(x) = g (x) として、

${\begin{cases}g(x)=f'(x),\\g'(x)=-f(x)\end{cases}}$

(2)

となる。(2) の第 1 式と第 2 式の両辺の積をとれば、積の微分法則から以下の関係が恒等的に成り立つことが示される。

$g'(x)g(x)+f'(x)f(x)=0\overbrace {\Longrightarrow } ^{\mbox{Leibniz rule}}g(x)^{2}+f(x)^{2}=\mathrm {constant} .$

(3)

ここで初期値として、

${\begin{cases}f(0)=0\\g(0)=f'(0)=1\end{cases}}$

(4)

を選べば、(3) は単位円に対する円の方程式となる。

$g(x)^{2}+f(x)^{2}=1.$

(5)

従って、方程式 (2), (4) を満たす関数 f (x), g (x) は単位円による定義での三角関数 sin, cos で表される。単位円による定義では sin 0 = 0, cos 0 = 1 なので、

${\begin{cases}f(x)=\sin x\\g(x)=\cos x\end{cases}}$

(6)

となる。他の三角関数はすべて sin, cos を用いて表すことができるので、(1) を出発して三角関数を定義することができた。三角関数の性質についても (6) と (2) から直ちに三角関数に関する微分公式

${\begin{cases}(\sin x)'=\cos x\\(\cos x)'=-\sin x\end{cases}}$

(7)

が得られる。

また、初期値問題の方程式は線型であることから

$y(x)=a\cos x+b\sin x$

とすれば、y(x) は再び初期値問題の方程式の解となる。 よって初期条件を

$a=\cos x_{0},b=-\sin x_{0}$

と選べば

$y(x)=\cos(x+x_{0})$

が解となり、このとき cos に関する加法定理

$\cos(x+x_{0})=\cos x_{0}\cos x-\sin x_{0}\sin x$

が導かれる。次に初期条件を

$a=\sin x_{0},b=\cos x_{0}$

と選べば解は

$y(x)=\sin(x+x_{0})$

となり、sin に関する加法定理

$\sin(x+x_{0})=\sin x_{0}\cos x+\cos x_{0}\sin x$

が導かれる。

ここで、y(x) = cos x と y(x) = sin x は (1) の 2 階の線型常微分方程式の基本解であり、これらの線型結合として一般解を書き表すことができる。一方で、ある初期条件に対して y(x) = e^ix という特殊解が得られるから、指数関数 e^ix は三角関数cos x, sin x の線型結合として表すことができる。この関係はオイラーの公式として知られている。オイラーの公式は、指数関数および三角関数を形式的に冪級数展開することでも示すことができ、この形式的な操作はそれらの関数の冪級数が収束することによって保証される。冪級数を用いた三角関数および指数関数の定義は、オイラーの公式を基本的な要請と見なす限りにおいては、オイラーの公式を通じて (1) の 2 階線型常微分方程式による定義と一致していることが確かめられる。ただし、冪級数を (1) を満たす解として構成する限りにおいては、両者の定義が一致することは明らかである。また、基本三角関数公式と加法定理が同一定義域において成り立つことが明らかであるから、関数関係不変の法則より両者の定義が一致することは明らかである。

この他にも定積分による（逆三角関数を用いた）定義などが知られている。

歴史

詳細は「三角法」および「三角関数の歴史」を参照

「円周率」および「円周率の歴史」も参照

バビロニア数学

一定の半径の円における中心角に対する弦と弧の長さの関係は、測量や天文学の要請によって古代から研究されてきた（バビロニア数学、Yale Babylonian Collection、YBC 7289）。紀元前1800年頃の粘土板「プリンプトン322」には、ピタゴラス数が記されていた。

古代ギリシャ・エジプト

古代ギリシャにおいて、円と球に基づく宇宙観に則った天文学研究から、ヒッパルコスにより一定の半径の円における中心角に対する弦の長さが表にまとめられたもの（正弦表、Trigonometric tables）が作られた。プトレマイオスの『アルマゲスト』にも正弦表が記載されている。

古代インド

正弦表は後にインドに伝わり、弦の長さは半分でよいという考えから5世紀頃には半弦 ardha-jiva（つまり現在の sine の意味の正弦）の長さをより精確にまとめたもの、すなわちアーリヤバタ（ヒンディー語: आर्यभट Āryabhaṭa）によって書かれたサンスクリット語の天文学書『アーリヤバティーヤ』（ヒンディー語: आर्यभटीय Āryabhaṭīya）、が作成された（Āryabhaṭa's sine table）。ardha は"半分" jiva は"弦"の意味で、当時のインドではこの半弦（現在の sine の意味の正弦）は単に jiva と略された。また、弦の長さを半分にして直角三角形を当てはめたことから派生して余角 (complementary angle) の考えが生まれ、“余角 (co-angle) の正弦 (sine)”という考えから余弦 (cosine) の考えが生まれた。余弦の値もこの頃に詳しく調べられている。（*co- は complementary の略で、補完的･補足的という意味の接頭語として用いる）

詳細は「ヴァラーハミヒラ」および「ブラーマグプタ」を参照

628年、ブラーマグプタ（ヒンディー語: ब्रह्मगुप्त Brahmagupta）が当時のインド数学と天文学の成果をまとめた代表的な著書『ブラーマ・スプタ・シッダーンタ』（ヒンディー語: ब्राह्मस्फुटसिद्धान्त Brāhmasphuṭasiddhānta）を発表。

中国

中国へは唐代（718年頃）に瞿曇悉達によってシッダーンタ（アーリヤバタの正弦表）が漢訳された『九執暦』が作られ、『開元占経』に含まれている。

イスラム帝国

770年代にファザーリとヤークブ・イブン・タリクが『ブラーマ・スプタ・シッダーンタ』をアラビア語に翻訳した『シンドヒンド』（アラビア語: السند هند‎ Zij al-Sindhind）を発表し、インドの知識がイスラーム世界にもたらされた。8世紀頃イスラム帝国へ伝わったときに jaib（入り江）と変化した。

10世紀のアッバース朝時代にシリアの数学者アル・バッターニが正弦法の導入、コタンジェント表の計算、球面三角法（球面幾何学）の定理を提唱した（Astronomy in medieval Islam、Zij、『サービア天文表 Az-Zij as-Sabi』）。ブワイフ朝のバグダードの数学者アブル・ワファーがタンジェントを導入した（al-Marwazi説もある）。

中世ヨーロッパ

スペインがタイファ期だった12世紀から13世紀にかけて、トレドで翻訳学派の学者が活躍した。一説では12世紀に、翻訳学派のひとり、チェスターのロバートが、アル・バッターニの著書をアラビア語からラテン語に翻訳した際、正弦を sinus rectus と意訳し（sinusはラテン語で「湾」のこと）、現在の sine になったという。

中世インド

「バースカラ2世」および「シッダーンタ・シロマーニ」も参照

「ケーララ学派」、「マーダヴァ」、「Madhava's sine table」、および「Madhava series」も参照

日本

日本では、江戸期に関孝和・建部賢弘・久留島喜内らが和算の「円理」と呼ばれる理論を発展させた。

近世ヨーロッパ

円や弦といった概念からは独立に、三角比を辺の比として角と長さの関係と捉えたのは16世紀オーストリアのゲオルク・レティクスであるといわれる。16世紀には地理学者メルカトルがメルカトル図法を考案して、大航海時代に始まった地図学の発展に大きな功績を残したが、メルカトルの時代には積分法は知られていなかったので「Secant関数の積分」が中心的な問題となった。 1638年にルネ・デカルトとジル・ド・ロベルヴァルが出題したデカルトの正葉線の問題が微積分法の発達を促し、インドのケーララ学派やイスラム帝国から伝わっていたそれまでの微分法と積分法という別々の二つの理論体系は、1670年頃にニュートンとライプニッツが独立に微積分法を発見・発明した結果、統合された。この微積分学によって、三角関数の理論は大きく発展した。17世紀後半にはアイザック・バローとジェームス・グレゴリーによって独立にSecant関数の積分が解決され、緯線距離はランベルト関数（逆グーデルマン関数）に相当することが明らかになった。また、余弦を co-sine と呼んだり、sin, cos という記号が使われるようになったりしたのは 17世紀になってからであり、それが定着するのは 18世紀オイラーの頃である。一般角に対する三角関数を定義したのはオイラーである。1748年にオイラーによって、指数関数と三角関数の間に等式が成り立つことが再発見された（オイラーの公式）。フランスの数学者ジョゼフ・フーリエによって金属板の中での熱伝導に関する研究の中でフーリエ級数が導入され、複雑な周期函数による波動の数学的表現が単純な「正弦函数や余弦函数の和」として表されるようになった（フーリエ解析）。1835年にはジェームズ・インマンが半正矢関数（haversine）を導入し、球面三角法での半正矢関数の公式を航海用として導入した。

現代

アーベルとヤコビによって発展させられた楕円函数論においても、円が三角関数で一意化される現象の類似物として、楕円曲線がモジュラー関数で一意化されることが発見された（「すべての楕円曲線はモジュラーである」）。まだ証明されていなかった時代に、この理論を応用したインド人のシュリニヴァーサ・ラマヌジャンらは、収束の早い円周率の公式を発見するなどした。それらの成果を発展させたアンドリュー・ワイルズは、「フェルマー予想」を証明することに成功した。

三角関数の性質

周期性

sin x と cos x のグラフ。これらの関数の周期性が確認できる。

x 軸の正の部分となす角は

$t=\theta +2\pi n\ (0\leq \theta <2\pi ,n\in \mathbb {Z} )$

と表すことができ、θ を偏角、t を一般角と言う。

一般角 t が 2π 進めば点 P(cos t, sin t) は単位円上を 1 周し元の位置に戻る。従って、

${\begin{aligned}\cos(t+2\pi n)&=\cos t\\\sin(t+2\pi n)&=\sin t\end{aligned}}$

すなわち三角関数 cos, sin は周期 2π の周期関数である。

ほぼ同様に、tan, cot は周期 π の周期関数、sec, csc は周期 2π の周期関数である。

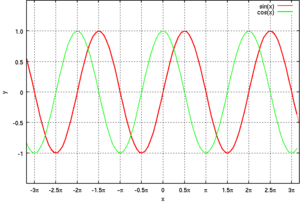
三角関数のグラフ: Sine（青実線）、 Cosine（緑実線）、 Tangent（赤実線）、 Cosecant（青点線）、 Secant（緑点線）、 Cotangent（赤点線）

相互関係

詳細は「三角関数の公式の一覧」を参照

単位円上の点の座標の関数であることから、三角関数の間には多数の相互関係が存在する。

基本相互関係

下記に示す基本三角関数公式はピタゴラスの定理やオイラーの公式などにより導かれる。 また、下記に示す基本三角関数公式はピタゴラスの基本三角関数公式 (Fundamental Pythagorean trigonometric identity) と呼ばれている。

• $\sin ^{2}\theta +\cos ^{2}\theta =1.$

証明 — 三角関数および指数関数は冪級数によって定義されているものとすると、負角公式と指数法則およびオイラーの公式より

${\begin{aligned}1&=e^{0}=e^{i\theta -i\theta }=e^{i\theta }e^{-i\theta }\\&=(\cos \theta +i\sin \theta )(\cos \theta -i\sin \theta )\\&=\sin ^{2}\theta +\cos ^{2}\theta \end{aligned}}$

であるから

$\sin ^{2}\theta +\cos ^{2}\theta =1$

が証明された。

上記の式を変形して整理すれば、以下の式が導かれる。

• $\sec ^{2}\theta -\tan ^{2}\theta ={\frac {1}{\cos ^{2}\theta }}-\tan ^{2}\theta =1,$
• $\csc ^{2}\theta -\cot ^{2}\theta ={\frac {1}{\sin ^{2}\theta }}-{\frac {1}{\tan ^{2}\theta }}=1.$

負角・余角・補角公式

負角

• ${\begin{cases}\sin(-\theta )=-\sin \theta \\\cos(-\theta )=\cos \theta \\\tan(-\theta )=-\tan \theta \end{cases}}$

証明 — sin および cos については、冪級数による表示から明らかである。また

${\begin{aligned}\tan(-\theta )&={\frac {\sin(-\theta )}{\cos(-\theta )}}\\&={\frac {-\sin \theta }{\cos \theta }}\\&=-\tan \theta \end{aligned}}$

である。

余角

• ${\begin{cases}\sin \left({\frac {\pi }{2}}-\theta \right)=\cos \theta \\\cos \left({\frac {\pi }{2}}-\theta \right)=\sin \theta \\\tan \left({\frac {\pi }{2}}-\theta \right)=\cot \theta \end{cases}}$

証明 — これは加法定理の特別な場合である。別の証明として、θ は実数とすると、オイラーの公式より

${\begin{aligned}\cos \left({\frac {\pi }{2}}-\theta \right)+i\sin \left({\frac {\pi }{2}}-\theta \right)&=e^{i({\frac {\pi }{2}}-\theta )}\\&=e^{\frac {i\pi }{2}}e^{-i\theta }\\&=i\cdot e^{-i\theta }\\&=i\cos \theta +\sin \theta \end{aligned}}$

であるから、実部と虚部を比較すれば

$\cos \left({\frac {\pi }{2}}-\theta \right)=\sin \theta ,\;\sin \left({\frac {\pi }{2}}-\theta \right)=\cos \theta$

である。また

${\begin{aligned}\tan \left({\frac {\pi }{2}}-\theta \right)&={\frac {\sin \left({\frac {\pi }{2}}-\theta \right)}{\cos \left({\frac {\pi }{2}}-\theta \right)}}\\&={\frac {\cos \theta }{\sin \theta }}\\&=\cot \theta \end{aligned}}$

である。よって、余角公式が証明された。

補角

• ${\begin{cases}\sin(\pi -\theta )=\sin \theta \\\cos(\pi -\theta )=-\cos \theta \\\tan(\pi -\theta )=-\tan \theta \end{cases}}$

証明 — これも加法定理の特別な場合である。別の証明として、θ は実数とすると、オイラーの公式より

${\begin{aligned}\cos(\pi -\theta )+i\sin(\pi -\theta )&=e^{i(\pi -\theta )}\\&=e^{i\pi }e^{-i\theta }\\&=-1\cdot e^{-i\theta }\\&=-\cos \theta +i\sin \theta \end{aligned}}$

より、実部と虚部を比較すれば

$\cos(\pi -\theta )=-\cos \theta ,\;\sin(\pi -\theta )=\sin \theta$

である。また

${\begin{aligned}\tan(\pi -\theta )&={\frac {\sin(\pi -\theta )}{\cos(\pi -\theta )}}\\&={\frac {\sin \theta }{-\cos \theta }}\\&=-\tan \theta \end{aligned}}$

である。よって、補角公式が証明された。

加法定理

• $\sin(x\pm y)=\sin x\cos y\pm \cos x\sin y$
• $\cos(x\pm y)=\cos x\cos y\mp \sin x\sin y$
• $\tan(x\pm y)={\frac {\tan x\pm \tan y}{1\mp \tan x\tan y}}$

証明 — オイラーの公式

$e^{ix}=\cos x+i\sin x$

Euler's formula

から

$\cos x={\frac {e^{ix}+e^{-ix}}{2}}$

$\sin x={\frac {e^{ix}-e^{-ix}}{2i}}$

であるので、指数法則から sin, cos の加法定理が得られ、これらから他の三角関数についての加法定理も得られる。

PQ（緑の線分の長さ）を求める。

また、三平方の定理から加法定理を示す方法が挙げられる。この方法では、円周上の任意の 2 点間の距離を 2 通りの座標系について求めることで、両者が等しいことから加法定理を導く。2 点間の距離を求めるのに三平方の定理を用いる。以下では単位円のみを取り扱うが、円の半径によらずこの方法から加法定理を得ることができる。

単位円の周上に 2 点 P = (cos p, sin p), Q = (cos q, sin q) を取る。P と Q を結ぶ線分の長さを PQ として、その 2 乗 PQ² を 2 通りの方法で求めることを考える（右図も参照）。

P と Q の x 座標の差と y 座標の差から、三平方の定理を用いて PQ² を求める。

${\begin{aligned}\mathrm {PQ} ^{2}&=\left(\cos p-\cos q\right)^{2}+\left(\sin p-\sin q\right)^{2}\\&=\left(\cos ^{2}p+\sin ^{2}p\right)+\left(\cos ^{2}q+\sin ^{2}q\right)-2\left(\cos p\cos q+\sin p\sin q\right)\\&=2-2\left(\cos p\cos q+\sin p\sin q\right).\end{aligned}}$

(1)

次に Q = (cos 0, sin 0) = (1, 0) となるような座標系を取り、同様に三平方の定理から PQ² を求める。この座標系に対する操作は、x 軸および y 軸を角度 q だけ回転させる操作に相当するので、P = (cos(p − q), sin(p − q)) となる。従って、

${\begin{aligned}\mathrm {PQ} ^{2}&=\left(\cos \left(p-q\right)-1\right)^{2}+\left(\sin \left(p-q\right)-0\right)^{2}\\&=2-2\cos \left(p-q\right)\end{aligned}}$

(2)

となる。

(1) と (2) の右辺が互いに等しいことから、次の cos に関する加法定理が得られる。

${\begin{aligned}\cos p\cos q+\sin p\sin q=\cos \left(p-q\right).\end{aligned}}$

(3)

三角関数の他の性質を利用することで、(3) から sin の加法定理なども導くことができる。

微積分

三角関数の微積分は、以下の表のとおりである。ただし、これらの結果には様々な（一見同じとは思えない）表示が存在し、この表における表示はいくつかの例であることに注意されたい。

$f(x)$	$f'(x)$	$\int f(x)\,dx$
$\sin x$	$\cos x$	$-\cos x+C$
$\cos x$	$-\sin x$	$\sin x+C$
$\tan x$	$\sec ^{2}x=1+\tan ^{2}x$	$-\ln \left|\cos x\right|+C$
$\cot x$	$-\csc ^{2}x=-(1+\cot ^{2}x)$	$\ln \left|\sin x\right|+C$
$\sec x$	$\sec x\tan x$	$\ln \left|\sec x+\tan x\right|+C=\operatorname {gd} ^{-1}x+C$
$\csc x$	$-\csc x\cot x$	$-\ln \left|\csc x+\cot x\right|+C=\ln \left|\tan {\frac {x}{2}}\right|+C$

ただし、gd⁻¹x はグーデルマン関数の逆関数である。

三角関数の微分では、次の極限

$\lim _{h\to 0}{\frac {\sin h}{h}}=1$

の成立が基本的である。このとき、sin x の導関数が cos x であることは加法定理から従う。さらに余角公式 cos x = sin(π/2 − x) から cos x の導関数は −sin x である。即ち、sin x は微分方程式 y''(x) + y(x) = 0 の特殊解である。また、他の三角関数の導関数も、上の事実から簡単に導ける。

下記に別の導出を示す。

微分の導出 — 実変数 x に対して、オイラーの公式

$e^{ix}=\cos x+i\sin x$

および

$(e^{ix})'=ie^{ix}$

を認めるならば

${\begin{aligned}(\cos x)'+i(\sin x)'&=(\cos x+i\sin x)'\\&=(e^{ix})'\\&=ie^{ix}\\&=i(\cos x+i\sin x)\\&=-\sin x+i\cos x\end{aligned}}$

となるから、両辺の実部と虚部を比較すれば

${\begin{cases}(\cos x)'=-\sin x\\(\sin x)'=\cos x\end{cases}}$

が得られる。 (tan x) ' は

${\begin{aligned}(\tan x)'&=\left({\frac {\sin x}{\cos x}}\right)'\\&={\frac {(\sin x)'\cos x-\sin x(\cos x)'}{\cos ^{2}x}}\\&={\frac {\cos ^{2}x+\sin ^{2}x}{\cos ^{2}x}}\\&={\frac {1}{\cos ^{2}x}}\\&=\sec ^{2}x\end{aligned}}$

である。 (cot x) ' は

${\begin{aligned}(\cot x)'&=\left({\frac {\cos x}{\sin x}}\right)'\\&={\frac {(\cos x)'\sin x-\cos x(\sin x)'}{\sin ^{2}x}}\\&={\frac {-(\sin ^{2}x+\cos ^{2}x)}{\sin ^{2}x}}\\&={\frac {-1}{\sin ^{2}x}}\\&=-\csc ^{2}x\end{aligned}}$

である。 (sec x) ' は

${\begin{aligned}(\sec x)'&=\left({\frac {1}{\cos x}}\right)'\\&={\frac {-(\cos x)'}{\cos ^{2}x}}\\&={\frac {-(-\sin x)}{\cos ^{2}x}}\\&={\frac {\tan x}{\cos x}}\\&=\sec x\tan x\end{aligned}}$

である。 (csc x) ' は

${\begin{aligned}(\csc x)'&=\left({\frac {1}{\sin x}}\right)'\\&={\frac {-(\sin x)'}{\sin ^{2}x}}\\&={\frac {-\cos x}{\sin ^{2}x}}\\&={\frac {-\cot x}{\sin x}}\\&=-\csc x\cot x\end{aligned}}$

である。

積分の導出 — sin x の積分は、(cos x)' = −sin x より

$\int \sin x\,dx=-\cos x+C$

である。 cos x の積分は、(sin x)' = cos x より

$\int \cos x\,dx=\sin x+C$

である。 tan x = sin x / cos x の積分は、u = cos x とおくと du/dx = −sin x であるから

${\begin{aligned}\int \tan x\,dx&=\int {\frac {\sin x}{\cos x}}\,dx\\&=-\int {\frac {1}{u}}\,du\\&=-\ln |u|+C\\&=-\ln |\cos x|+C\\&=\ln |\cos x|^{-1}+C\\&=\ln |\sec x|+C\end{aligned}}$

である。 cot x の積分は、u = sin x とおくと du/dx = cos x であるから

${\begin{aligned}\int \cot x\,dx&=\int {\frac {\cos x}{\sin x}}\,dx\\&=\int {\frac {1}{u}}\,du\\&=\ln |u|+C\\&=\ln |\sin x|+C\end{aligned}}$

である。 sec x = 1/cos x の積分は、u = sin x とおくと du/dx = cos x であるから

${\begin{aligned}\int \sec x\,dx&=\int {\frac {\cos x}{\cos ^{2}x}}\,dx\\&=\int {\frac {\cos x}{1-\sin ^{2}x}}\,dx\\&=\int {\frac {du}{1-u^{2}}}\\&=\int {\frac {du}{(1-u)(1+u)}}\end{aligned}}$

ここで、部分分数分解をすれば

${\begin{aligned}\int {\frac {du}{(1-u)(1+u)}}&={\frac {1}{2}}\int \left({\frac {1}{1-u}}+{\frac {1}{1+u}}\right)du\\&={\frac {1}{2}}(-\ln |1-u|+\ln |1+u|)+C\\&={\frac {1}{2}}\ln \left|{\frac {1+u}{1-u}}\right|+C\end{aligned}}$

となる。したがって

${\begin{aligned}\int \sec x\,dx&={\frac {1}{2}}\ln \left|{\frac {1+u}{1-u}}\right|+C\\&={\frac {1}{2}}\ln {\frac {1+\sin x}{1-\sin x}}+C\\&={\frac {1}{2}}\ln {\frac {(1+\sin x)^{2}}{1-\sin ^{2}x}}+C\\&={\frac {1}{2}}\ln \left({\frac {1+\sin x}{\cos x}}\right)^{2}+C\\&=\ln |\sec x+\tan x|+C\end{aligned}}$

である。 csc x = 1/sin x の積分は、u = cos x とおくと du/dx = −sin x であるから

${\begin{aligned}\int \csc x\,dx&=\int {\frac {\sin x}{\sin ^{2}x}}\,dx\\&=\int {\frac {\sin x}{1-\cos ^{2}x}}\,dx\\&=-\int {\frac {1}{1-u^{2}}}\,du\\&=-{\frac {1}{2}}\ln \left|{\frac {1+u}{1-u}}\right|+C\\&=-{\frac {1}{2}}\ln {\frac {1+\cos x}{1-\cos x}}+C\\&=-{\frac {1}{2}}\ln {\frac {(1+\cos x)^{2}}{1-\cos ^{2}x}}+C\\&=-{\frac {1}{2}}\ln \left({\frac {1+\cos x}{\sin x}}\right)^{2}+C\\&=-\ln |\csc x+\cot x|+C\end{aligned}}$

である。また、半角の公式を用いれば

${\begin{aligned}\int \csc x\,dx&={\frac {1}{2}}\ln {\frac {1-\cos x}{1+\cos x}}+C\\&={\frac {1}{2}}\ln {\frac {\sin ^{2}{\frac {x}{2}}}{\cos ^{2}{\frac {x}{2}}}}+C\\&=\ln \left|\tan {\frac {x}{2}}\right|+C\end{aligned}}$

である。

(sin x) / x の x → 0 における極限

日本の中等教育について、「一般的に教科書に載っている、極限の値

$\lim _{x\to 0}{\frac {\sin x}{x}}=1$

の証明は循環論法であるため論理が破綻している」という主張がなされることがある。ここで言う「教科書に載っている証明」とは、中心角 x ラジアンの扇形の面積を2つの三角形の面積ではさみ、いわゆるはさみうちの原理から証明するものであるが、ここで問題となるのは、証明に面積が利用されていることである（時にはラジアンが利用されていることも問題とされることもある）。ここで面積は積分によって定義されるものであるとすると、特に扇形の面積を求めるには三角関数の積分が必要となり、三角関数の積分をするには三角関数の微分ができねばならず、三角関数を微分するにはもとの極限が必要になる。このことが循環論法と呼ばれているのである。
この循環論法を回避する方法として正弦関数と余弦関数を上述のような無限級数で定義する方法があるが、高校範囲を超えてしまう。

無限乗積展開

詳細は「三角関数の無限乗積展開」を参照

三角関数は以下のように無限乗積として書ける。

$\sin \pi z=\pi z\prod _{n=1}^{\infty }{\left(1-{\frac {z^{2}}{n^{2}}}\right)}$

$\cos \pi z=\prod _{n=1}^{\infty }\left\{1-{\frac {z^{2}}{(n-{\frac {1}{2}})^{2}}}\right\}$

部分分数展開

詳細は「三角関数の部分分数展開」を参照

三角関数は以下のように部分分数に展開される。

$\pi \cot \pi z=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {1}{z+n}}={\frac {1}{z}}+\sum _{n=1}^{\infty }{\frac {2z}{z^{2}-n^{2}}}$

$\pi \tan \pi z=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {-1}{z+\textstyle {\frac {1}{2}}+n}}=-\sum _{n=0}^{\infty }{\frac {2z}{z^{2}-\left(n+\textstyle {\frac {1}{2}}\right)^{2}}}$

${\frac {\pi }{\sin \pi z}}=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {(-1)^{n}}{z+n}}={\frac {1}{z}}+\sum _{n=1}^{\infty }{\frac {(-1)^{n}2z}{z^{2}-n^{2}}}$

${\frac {\pi }{\cos \pi z}}=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {(-1)^{n}}{z+{\frac {1}{2}}+n}}=-\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n+1)}{z^{2}-\left(n+{\frac {1}{2}}\right)^{2}}}$

逆三角関数

詳細は「逆三角関数」を参照

三角関数の定義域を適当に制限したものの逆関数を逆三角関数（ぎゃくさんかくかんすう、英: inverse trigonometric function）と呼ぶ。逆三角関数は逆関数の記法に則り、元の関数の記号に −1 を右肩に付して表す。たとえば逆正弦関数（ぎゃくせいげんかんすう、英: inverse sine; インバース・サイン）は sin⁻¹x などと表す。arcsin, arccos, arctan などの記法もよく用いられる。数値計算などにおいては、これらの逆関数は更に asin, acos, atan などと書き表される。

$x=\sin y\iff y=\sin ^{-1}x$

$x=\cos y\iff y=\cos ^{-1}x$

$x=\tan y\iff y=\tan ^{-1}x$

$x=\cot y\iff y=\cot ^{-1}x$

$x=\sec y\iff y=\sec ^{-1}x$

$x={\text{cosec}}\,y\iff y={\text{cosec}}^{-1}\,x$

である。逆関数は逆数ではないので注意したい。逆数との混乱を避けるために、逆正弦関数 sin⁻¹x を arcsin x と書く流儀もある。一般に周期関数の逆関数は多価関数になるので、通常は逆三角関数を一価連続なる枝に制限して考えることが多い。たとえば、便宜的に主値と呼ばれる枝を

$-{\frac {\pi }{2}}\leq \sin ^{-1}x\leq {\frac {\pi }{2}}$

$0\leq \cos ^{-1}x\leq \pi$

$-{\frac {\pi }{2}}<\tan ^{-1}x<{\frac {\pi }{2}}$

のように選ぶことが多い。またこのとき、制限があることを強調するために、Sin⁻¹x, Arcsin x のように頭文字を大文字にした表記がよく用いられる。

複素関数としての三角関数

cos z, sin z の級数による定義から、オイラーの公式 exp(iz) = cos z + i sin z を導くことができる。この公式から下記の 2 つの等式

${\begin{aligned}\exp(iz)&=e^{iz}=\cos z+i\sin z\\\exp(-iz)&=e^{-iz}=\cos z-i\sin z\end{aligned}}$

が得られるから、これを連立させて解くことにより、正弦関数・余弦関数の指数関数を用いた表現が可能となる。即ち、

${\begin{aligned}\cos z&={\frac {e^{iz}+e^{-iz}}{2}},\\\sin z&={\frac {e^{iz}-e^{-iz}}{2i}}.\end{aligned}}$

が成り立つ。この事実により、級数によらずこの等式をもって複素変数の正弦・余弦関数の定義とすることもある。また、

${\begin{aligned}\cos(iz)&={\frac {e^{-z}+e^{z}}{2}}=\cosh z,\\\sin(iz)&={\frac {e^{-z}-e^{z}}{2i}}=i\sinh z\end{aligned}}$

が成り立つ。ここで cosh z, sinh z は双曲線関数を表す。この等式は三角関数と双曲線関数の関係式と捉えることもできる。複素数 z を z = x + iy (x, y ∈ R) と表現すると、加法定理より

${\begin{aligned}\cos z&=\cos(x+iy)=\cos x\cosh y-i\sin x\sinh y,\\\sin z&=\sin(x+iy)=\sin x\cosh y+i\cos x\sinh y\end{aligned}}$

が成り立つ。

他の三角関数は csc z = 1 / sin z, sec z = 1 / cos z, tan z = sin z / cos z, cot z = cos z / sin z によって定義できる。

• 
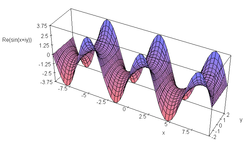
  cos(x + iy) の実部のグラフ
• 
  cos(x + iy) の虚部のグラフ
• 
  sin(x + iy) の実部のグラフ
• 
  sin(x + iy) の虚部のグラフ

球面三角法

詳細は「球面三角法」を参照

球面の三角形 ABC の内角を a, b, c, 各頂点の対辺に関する球の中心角を α, β, γ とするとき、次のような関係が成立する。余弦公式や正弦余弦公式は式の対称性により各記号を入れ替えたものも成立する。

正弦公式

sin a : sin b : sin c = sin α : sin β : sin γ

余弦公式

cos a = −cos b cos c + sin b sin c cos α

余弦公式

cos α = cos β cos γ + sin β sin γ cos a

正弦余弦公式

sin a cos β = cos b sin c − sin b cos c cos α

参考文献

• ノイゲバウアー, オットー『古代の精密科学』恒星社厚生閣、1984年2月。ISBN 978-4769906803。 
• Maor, Eli (1998). Trigonometric Delights. Princeton University Press. ISBN 9780691057545 
• 志賀, 浩二『数の大航海―対数の誕生と広がり』日本評論社、1999年7月。ISBN 978-4-535-78289-1。 
• ジョーゼフ, ジョージ・G『非ヨーロッパ起源の数学―もう一つの数学史』講談社〈ブルーバックス〉、1996年5月。ISBN 978-4062571203。 
• 高瀬, 正仁『古典的難問に学ぶ微分積分』共立出版、2013年7月。ISBN 978-4-320-11041-0。 
• Vinogradov, Ivan Matveyevich (2004-09-10). The Method of Trigonometrical Sums in the Theory of Numbers (revised ed.). Dover. ISBN 978-0486438788 
• 黒川, 信重、小山, 信也『多重三角関数論講義』日本評論社、2010年11月8日。ISBN 978-4535785557。 
• 杉浦, 光夫『解析入門I』東京大学出版会〈基礎数学2〉、1980年。ISBN 978-4-13-062005-5。 

関連項目

• 正弦定理
• 余弦定理
• 正接定理
• 球面三角法
• コサイン4乗則
• ベクトルのなす角 - cos 関数を用いて表現される。
• ドット積
• クロス積

外部リンク

• Weisstein, Eric W. "Trigonometric Functions". mathworld.wolfram.com (英語).
• 三角比の近似値表