フーコーの振り子

フランスパリのパンテオンのフーコーの振り子。1851年、初めて一般向けの公開実験が行われた場所である。1995年よりフーコーの振り子が再現されている。

フーコーの振り子（フーコーのふりこ、仏: Pendule de Foucault、英: Foucault pendulum）は、地球の自転現象を示す演示実験である。自転運動する物体上で、長い弦をもつ周期の長い振り子を長時間振動させると、次第に振動面が変化することが観察できる。1851年、フランスのレオン・フーコーが考案し、パリのパンテオンで公開実験を行った。

概要

北極点におけるフーコー振り子のシミュレーション

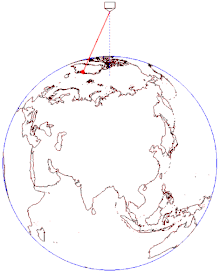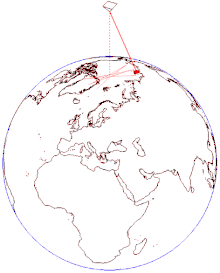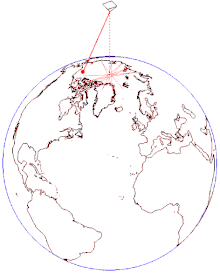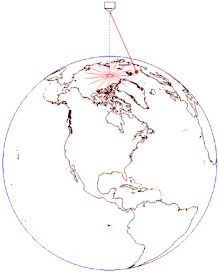
振り子を長時間振動させつづけると、その振動面が少しずつ回転する。例えば、北極点の真上に振り子を置いて振動させると、振り子は一定方向に振動を続けるが、振動面は24時間で地球の自転方向とは逆向きに360度回転する。これは振り子の振動面が支点を通る鉛直軸まわりの回転から影響を受けないために起こる。振り子の錘は外力を受けなければ、いつまでも直線運動を続ける。これは慣性の法則から明らかである。一方、振り子の錘は支点に向かって力を受けているが、これは振動面の面内に働く力であり振動面を変える効果はない。

振動面の変化は、振り子上面からみて北半球の場合は右回り、南半球では左回りとなる。赤道上においては振動面の回転は発生しない。緯度$\theta$において、フーコーの振り子の振動面の回転は1日あたり$360^{\circ }\sin \theta$、1時間あたり$15^{\circ }\sin \theta$となる（参照：#フーコーの正弦則）。この関係から逆算して、建物の中で振り子を振動させて、振動面の回転速度を観測すると、振り子のある地点の緯度と北半球か南半球かがわかる。

一般にフーコーの振り子の振動面の回転を理解することは難しい。特に中緯度における振動面の回転現象の説明は困難である。例えば古生物学者で作家のスティーヴン・ジェイ・グールドはニューヨーク・タイムズへのインタビューに「（アメリカ国内に数多く展示されている）フーコーの振り子について、私はそれがどのような理屈なのか理解できていないし、ほとんどの訪問者も同じだと思う」と述べている。

ターンテーブルの上で揺れる振り子をテーブル上の観測者の視点からは、振り子の振動面がテーブルと同じ角速度で回転して観測できることは、比較的容易に理解できる。しかし、前述のようにフーコーの振り子の振動面の回転は緯度への依存性があり、理解が難しい。例えば、東京を通る北緯35度で、減衰しない理想的な振り子を振動させたとき、振動面は1時間あたり8.6度、1日で206.5度回転する。つまり振り子の振動面は前日とは異なる位置になるが、夜空の星座の位置は24時間経過すると、ほぼ同じ位置に戻っている。この違いもフーコーの振り子を直感的に理解することを困難にさせる要因である。

原理上、地球上で振動している振り子は、すべてフーコーの振り子といえる。しかし、振り子によって地球の自転を観察するためには、振り子を長時間振動させる必要があり、また錘の楕円運動など阻害要因を可能な限り除去する必要がある。振り子の振動において楕円運動が生じると、地球が自転していなくても振動面が徐々に回転する。このため、基本的に長い弦と質量の大きい錘が求められる。

他方、フーコーの振り子の装置は通常大型となり、また振り子による地球の自転の観測は時間がかかる。このため、チャールズ・ホイートストンが1851年に発表した装置（#ホイートストンの装置を参照）をはじめとして、模型を使って簡易的に原理を説明する試みも多数発表されている。以下にターンテーブルを使った模型によるフーコーの振り子のデモンストレーションを撮影した動画を示す。

フーコーの振り子の模型によるシミュレーション動画

ターンテーブル上での振り子の動き

ターンテーブル上（回転座標系）で振り子を横方向から観察したもの

ターンテーブル上（回転座標系）で振り子を下から見上げて観察したもの

理論

単振り子の等時性

弦の下端に錘を、上端を固定して吊るし、同一鉛直平面内で振動させたものを単振り子という。単振り子の弦の長さを$l$、重力加速度を$g$とすると、振り子の周期$T$は、次式で表現できる。

$T=2\pi {\sqrt {\frac {l}{g}}}$$\qquad \cdots \$(1-1)

これは単振り子の周期は、錘の質量の大小に関わらず弦の長さのみで周期がきまることを示している。また振れ幅の大小も、単振り子の周期とは無関係であり、これを「単振り子の等時性」という。17世紀初めにガリレオ・ガリレイによって確立された。

振り子の振動面の変化で地球の自転を目視するためには、振り子が長時間動作し、振動面の回転角度の変化が確認できる程度の振れ角が必要である。この条件を有利に働かせるために、弦の長さを長くする必要がある。

フーコーの正弦則

「フーコーの正弦則」による緯度と振動面の移動の関係を示したもの。赤実線：振り子の振動面が一周するのに要する時間。青点線：一日に振り子の振動面が回転する角度。

北緯30度での振動面の変化を表したアニメーション。2日（48時間）で一周する。

「フーコーの正弦則」とは振り子の置かれた緯度と振動面の変化の関係式のことである。フーコーが1851年に「Démonstration physique du mouvement de rotation de la Terre au moyen du pendule（振り子による地球の回転運動の物理的実証）」と題して発表し、直後にジョゼフ・リウヴィルが証明方法を発表している。

地球の北半球上の緯度$\theta$に支点のある振り子が南北に振動していると考える。地球の半径を$R$、地球の自転による角速度を$\omega$、振り子の振幅を$r$とする。

地球の中心点を原点とした座標系において、支点の直下での錘は自転により以下の速度で移動する。

$\omega R\cos \theta$

次に、振り子の錘が最も北にきたときの自転から受ける速度は以下の式になる。

$\omega R\cos \theta -\omega r\sin \theta$

また、振り子の錘が最も南にきたときの点での自転から受ける速度は以下の式になる。

$\omega R\cos \theta +\omega r\sin \theta$

つまり、振り子の錘は北側より南側に振れた点の方が速く移動していることになる。振り子の支点直下からみて、両点が地球の自転から受ける速度は以下になる。

$\omega r\sin \theta$

振り子の振動面が地球の自転の影響をうけて一周するとき、移動は円となりその円周は$2\pi r$、一周に要する時間を$T_{rot}$とすると、上式をつかって以下のように表現できる。

$T_{rot}={\frac {2\pi r}{\omega r\sin \theta }}$

地球の自転は約24時間であり、$\omega =2\pi /24$となるので、振り子の振動面が一周するのに必要な時間$T_{rot}$は以下のようになる。

$T_{rot}={\frac {24}{\sin \theta }}$$\qquad \cdots \$(2-1)

式(2-1)を「フーコーの正弦則」と呼ぶ。また緯度$\theta$での1時間あたりの振動面の回転角度$\alpha _{rot}$は以下のようになる

$\alpha _{rot}=15^{\circ }\sin \theta$$\qquad \cdots \$(2-2)

ただし、厳密には恒星に対して地球の自転は23時間56分4秒 = 23.934時間である。従って、「フーコーの正弦則」についても、厳密にはこの値を用いる。

$T_{rot}={\frac {23.934}{\sin \theta }}$

円錐を使った説明

フーコーの正弦則について円錐を用いた説明（ドイツ語） 円錐によるフーコーの振り子の説明のためのペーパーモデルの型。緑色の矢印が振り子の振動面に相当する。0度の部分を基準に任意の緯度の部分に合わせて円錐形にすると、振り子の振動面の変化が現れる。円錐の扇形の部分を平面展開した場合、振り子の振動面はすべて同じ方向となる。

フーコーの正弦則で示したように、フーコーの振り子の振動面の回転は緯度依存性がある。このため、極点上および赤道上以外の場所における振動面の回転については、もう一歩踏み込んだ解説が必要となる。この解説の一つとして「フーコーの正弦則」の説明に円錐を使った方法も用いられることがある。

地球上の実験地点の緯度$\theta$と同一緯度の線に沿って接し、地球の自転軸と共通の軸を持つ円錐を考える。円錐を展開すると側面は扇形となり、扇形の中心角$\alpha$は扇形の弧の長さと扇形の半径の比に等しい。扇形の弧の長さは円錐底面の円周と等しい。また円錐の軸と円錐の母線（扇形の半径）のなす角は緯度$\theta$に等しく、さらに円錐底面の円の半径と扇形の半径の比は$\sin \theta$と等しい。従って、扇形の中心角$\alpha$との関係は以下の式となる。

$\alpha =2\pi \sin \theta =360^{\circ }\sin \theta$

ここで緯度$\theta$でのフーコー振り子の振動面を円錐を使って考える。振り子の振動面は、円錐の底面と側面の境界線を移動しながら、境界線と直交し常に頂点方向に振幅していると考えることができる。従って、地球が一回転したときの、緯度$\theta$での振り子の振動面の回転量は、円錐側面の扇形の中心角$2\pi \sin \theta$と等しくなる。これより振り子の振動面が一周するのに必要な時間$T_{rot}$は、以下のようになる。

$T_{rot}=24\times {\frac {1}{\alpha \div 360^{\circ }}}={\frac {24}{\sin \theta }}$$\qquad \cdots \$(3-1)

つまり、振り子の観察者は円錐の上に立って地球の自転による移動をしていることと同等である。円錐の扇形の部分を平面展開した場合、振り子の振動面はすべて同じ方向となる。すなわちこれは、赤道における振り子の振動面の変化（変化なし）である。

円錐によるフーコーの振り子の理解のためには、実際に円錐を作って試してみると理解が進む。厚紙を使って円錐をつくっても良いが、透明なプラスチックシートと地球儀を使うことも有効である。

前述のようにターンテーブルによってフーコーの振り子を模擬する方法があるが、さらに改良して中緯度でのフーコーの振り子を模擬する方法も提案されている。地球儀にアクリルの円板を任意の中緯度に接するように取り付ける。さらに、円板の中央に振り子を支持するための治具を取り付ける。振り子を振動させて、地球儀を一周させると、アクリル円板はフーコーの正弦則とほぼ等しい回転を行う。

コリオリの力による解説

北極点、北緯50度、北緯30度、北緯15度、赤道、南緯15度の6地点でのフーコーの振り子の振動面の回転の違いを示したシミュレーション

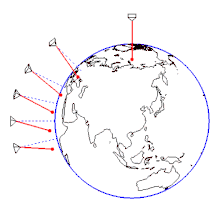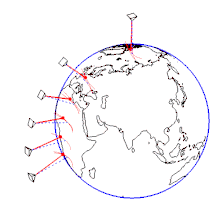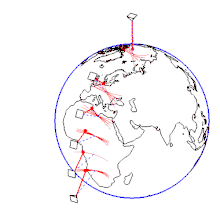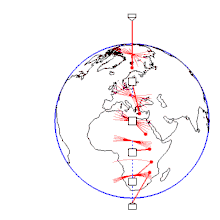
コリオリの力を使ったフーコーの振り子のモデルを考える。緯度$\theta$にある振り子の運動を考える。錘の質量を$m$、弦の長さ$l$、弦に働く張力を$F$、地球の自転の角速度を$\omega$とする。また振り子の支点の真下に錘の質点がくる点を原点とした座標系を設定する。振り子の振動が弦の長さに比べて十分に小さく、振り子の錘の運動は$xy$平面内の運動としてみなす。すなわち、座標系の原点回りの回転による遠心力と、$z$軸成分を省略した錘の運動は以下の運動方程式となる。

$m{\frac {d^{2}x}{dt^{2}}}=-F{\frac {x}{l}}+2m\omega \sin \theta {\frac {dy}{dt}}$$\qquad \cdots \$(4-1)

$m{\frac {d^{2}y}{dt^{2}}}=-F{\frac {y}{l}}-2m\omega \sin \theta {\frac {dx}{dt}}$$\qquad \cdots \$(4-2)

ここで第2項がコリオリの力となる。yを乗じた式(4-1)からxを乗じた式(4-2)と差をとり、張力を除いた式は

${\frac {d}{dt}}\left(x{\frac {dy}{dt}}-y{\frac {dx}{dt}}\right)=-\omega \sin \theta {\frac {d}{dt}}(x^{2}+y^{2})$

これを積分する。ただし錘が$(x,y,z)=(0,0,0)$を通過すると仮定すると、積分定数は0となる。

$x{\frac {dy}{dt}}-y{\frac {dx}{dt}}=-\omega \sin \theta (x^{2}+y^{2})$

ここで$xy$平面上に極座標$(r,\phi )$をとり、$x=r\cos \phi ,y=r\sin \phi$を上式に代入すると以下の式を得る。

${\frac {d\phi }{dt}}={\dot {\phi }}=-\omega \sin \theta$$\qquad \cdots \$(4-3)

${\dot {\phi }}$は、自転による振り子の振動面の回転角速度であり、絶対値をみると「フーコーの正弦則」と一致する。また符号から北半球（$\theta >0$）では時計回り、南半球（$\theta <0$）では反時計回りに回転し、赤道上（$\theta =0$）では回転しないことを示している。

錘の軌道

→「§ オネスによるフーコーの振り子の研究」も参照

振り子の振動に比べて、座標系の回転を高速にしたフーコーの振り子のシミュレーション（北半球）。錘の進行方向に対して右側にそれる。また回転座標系からは軌道がサイクロイド曲線となる。ハーモノグラフも参照。

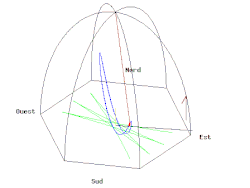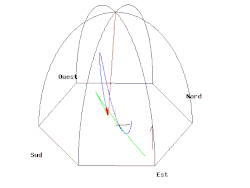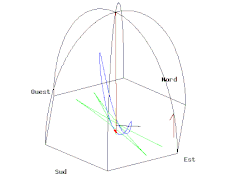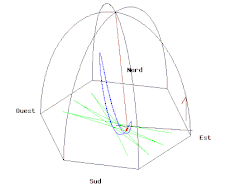
振り子の錘の軌道を複素平面上において考える。複素数$\eta$を以下のように定義する。

$\eta =x+i\cdot y$$\qquad \cdots \$(5-1)

振り子の振幅が小さい場合、弦に働く張力$F=mg$に近似できる。式(4-2)に$i$を乗じて、式(4-1)と式(4-2)を複素数$\eta$で表すと以下のようになる。ただし$g$は重力加速度である。

${\frac {d^{2}\eta }{dt^{2}}}=-2i\omega \sin \theta {\frac {d\eta }{dt}}-{\frac {g}{l}}\eta$

ここで${\dot {\phi }}=-\omega \sin \theta$、$\psi ={\sqrt {g/l}}$と置くと、

${\frac {d^{2}\eta }{dt^{2}}}+2i{\dot {\phi }}{\frac {d\eta }{dt}}+\psi ^{2}\eta =0$

これは定数係数2階線形同次微分方程式であり、特性方程式を以下のように表現する。

$\lambda ^{2}+2i{\dot {\phi }}\lambda +\psi ^{2}=0$

$\lambda$について解く。ここで${\dot {\phi }}$は緯度$\theta$における自転による角速度であるため${\dot {\phi }}^{2}\simeq 0$と近似できる。

$\lambda =-i{\dot {\phi }}\pm {\sqrt {-{\dot {\phi }}^{2}-\psi ^{2}}}\simeq -i({\dot {\phi }}\mp \psi )$

この微分方程式の解として以下の式となる。ただし$A$、$B$は複素数の積分定数である。

$\eta =e^{-i{\dot {\phi }}t}\left(Ae^{i\psi t}+Be^{-i\psi t}\right)=Ae^{i(\psi -{\dot {\phi }})t}+Be^{-i(\psi +{\dot {\phi }})t}$

オイラーの公式を適用する。ただし$A=A_{1}+iA_{2}$、$B=B_{1}+iB_{2}$とし、式(5-1)より

$x(t)=A_{1}\cos(\psi -{\dot {\phi }})t-A_{2}\sin(\psi -{\dot {\phi }})t+B_{1}\cos(\psi +{\dot {\phi }})t+B_{2}\sin(\psi +{\dot {\phi }})t$

$y(t)=A_{1}\sin(\psi -{\dot {\phi }})t+A_{2}\cos(\psi -{\dot {\phi }})t-B_{1}\sin(\psi +{\dot {\phi }})t+B_{2}\cos(\psi +{\dot {\phi }})t$

次に、振り子の始動時について考察する。ここで振り子の振動数に比べて地球の自転角速度は無視できるほど小さい（$\psi \gg {\dot {\phi }}$）。つまり${\dot {\phi }}\simeq 0$と考えると、

$x(t)=(A_{1}+B_{1})\cos \psi t-(A_{2}+B_{2})\sin \psi t$

$y(t)=(A_{1}-B_{1})\sin \psi t+(A_{2}-B_{2})\cos \psi t$

時刻$t=0$のとき、$y(0)=0$かつ${\dot {x}}(0)=0$とすると、$A_{2}=B_{2}=0$であるので

$x(t)=(A_{1}+B_{1})\cos \psi t$$\qquad \cdots \$(5-2)

$y(t)=(A_{1}-B_{1})\sin \psi t$$\qquad \cdots \$(5-3)

$A_{1}\neq B_{1}$のとき、$x$と$y$は以下の関係に整理することができる。

${\frac {x^{2}}{(A_{1}+B_{1})^{2}}}+{\frac {y^{2}}{(A_{1}-B_{1})^{2}}}=1$

すなわち$A_{1}\neq B_{1}$のとき振り子の錘の軌道が楕円になることを示している。また$A_{1}=B_{1}$のとき直線となる。

式(5-2)、式(5-3)を時間微分すると

${\dot {x}}(t)=-\psi (A_{1}+B_{1})\sin \psi t$$\qquad \cdots \$(5-4)

${\dot {y}}(t)=\psi (A_{1}-B_{1})\cos \psi t$$\qquad \cdots \$(5-5)

時刻$t=0$のとき式(5-2)から式(5-5)より初期条件は以下のようになる。

$x(0)=(A_{1}+B_{1}),y(0)=0$

${\dot {x}}(0)=0,{\dot {y}}(0)=\psi (A_{1}-B_{1})$

つまり、$x$方向に錘を持ち上げてから振り下ろすことを意味し、一方で$y$方向に$\psi (A_{1}-B_{1})$の初期速度が生じるため、楕円運動になる。従って楕円運動を避けるためには、$y$方向に速度が生じないようにする錘を振り下ろする必要がある。

ただし実際の振り子では、錘の振り下ろし以外にも「弦を固定する支持装置が$x$方向と$y$方向で異なる干渉が働く」「錘が完全な対称形状をしておらず、振動に伴って生じる空気抵抗が非対称に作用する」「振り子の周りの空気の流れ」などの原因によって、楕円運動が生じる。

楕円運動

→「§ オネスによるフーコーの振り子の研究」も参照

振り子の振動において楕円運動が生じると、地球が自転していなくても振動面が徐々に回転する。この現象を球面振り子の楕円運動による面積効果と呼ぶ。

ここで、振り子の弦の長さを$l$、振り子の楕円軌道の長軸側の初期振幅を$x_{0}$とする。面積効果による振り子の振動面の回転角速度$\Omega$は以下の式で表現できる。

$\Omega ={\frac {3}{8}}{\frac {x_{0}^{2}}{l^{2}}}\omega \sin \theta$

これより式(4-3)を拡張し、振り子の楕円運動も含めた緯度$\theta$における振動面の角速度の式（フーコーの正弦則の拡張）は以下の通りとなる。

${\dot {\phi }}=-\omega \sin \theta \left(1-{\frac {3}{8}}{\frac {x_{0}^{2}}{l^{2}}}\right)$$\qquad \cdots \$(6-1)

弦長と振幅について$l\gg x_{0}$、すなわち弦長が振幅に対して十分長ければ振り子の楕円運動による面積効果は無視できるが、弦長が短い場合は補正が必要となる。

装置

フーコーの振り子は、振動面の回転を観察するためには長時間振動が継続する必要があり、振動の減衰率は可能な限り低いことが望ましい。振り子の振動の減衰は、支持装置の機械的な摩擦抵抗と、弦と錘に作用する空気抵抗が主要因である。また支持装置の構造や空気抵抗、振り子の特性、振り子の起動などにより錘の軌道が楕円運動するため、これを抑制する仕組みも必要となる。

弦と錘

フーコーの振り子では、振動が長時間継続することが必要であり、基本的に長い弦と質量の大きい錘が求められる。

振り子の空気抵抗は、投影面積と速度の2乗の積に比例する。弦は、同じ長さの弦であれば径が小さい方が良い。また振り子の振幅長が同一で比較すると、弦が長いほど平均速度が小さくなり、空気抵抗を減らすことができる。しかし、長い弦による空気抵抗は無視できない。錘は、比重の大きな材質を使い、断面積が小さく質量が大きくなるように設計する。

支持装置

フーコーの振り子用のダブルナイフエッジによる支持装置（国立科学博物館で使用している装置の模式図）。上：振り子の弦と直接固定するナイフエッジ、中：中間リング、下：受け側のナイフエッジ

ヘイケ・カメルリング・オネスが実験に使用したフーコーの振り子のダブルナイフエッジによる支持装置。板バネの押し付けの調整により、楕円軌道の研究を行った。

支持装置は振り子の弦を固定する部分であり、任意の方向に振り子を振動させることが必要がある。また横振動を抑止し、長時間振動を続けるために、隙間なく1点で固定し、かつ機械的摩擦抵抗が小さいことが望まれる。振り子の弦の支持装置として「固定型」、「やじろべえ型」、「ナイフエッジ型」、「自在継手」などが考えられる。

「固定型」による弦の支持は、弦を単純にボルトで締め付けたり、チャックで固定することで、弦の弾性変形より振り子を振動させる方法である。構造が単純で1点支持のため減衰が少ない。しかし、弦をボルト留めする場合、弦にボルトを通す穴が必要となり、この穴の隙間の影響による楕円運動の発生の可能性がある。また弦に直接曲げ力が働くため疲労破壊の可能性もある。

「やじろべえ型」は振り子の弦をお椀型または円環型の器具に固定し、この器具 を上向きの針で1点固定する方法である。しかし「やじろべえ型」では、振り子の振動面が回転すると針を支える構造体と干渉を起こす。このためフーコーの振り子には不向きな支持構造である。

「ナイフエッジ」は弦の上端を三角柱の部材で固定し、この三角柱の角（ナイフエッジ）で、受け部材に載せて支持するものである。「ナイフエッジ」による支持装置は、機械的な摩擦抵抗が非常に小さいが、エッジや受け側の摩耗やそれらの間への塵の侵入などが問題となる。フーコーの振り子の場合は、振動面の回転方向へ働く抗力も減らす必要があるため、「ダブルナイフエッジ」を使用する。「ダブルナイフエッジ」とは、互いに向き合った2組のナイフエッジを直交させて中間リングで受けて、1点で回転中心になるようにしたものである。

ヘイケ・カメルリング・オネスはフーコーの振り子の研究で博士号を取得しているが（後述）、使用したフーコーの振り子はダブルナイフエッジによる支持装置を採用している。ナイフエッジ側に板バネを取り付け、中間リングを両側から押し付けを調整できるようになっている。これを調整することにより、フーコーの振り子における楕円軌道の研究を行った。

国立科学博物館のフーコーの振り子も、機械摩擦低減のため「ダブルナイフエッジ」による支持装置に採用している。これは1934年に設置されたが、ドイツの機械工学雑誌に掲載されたものを参考に、東京計器製作所（現：東京計器）が製作した。

国際連合本部ビルにあるフーコーの振り子の支持装置は自在継手を採用している。

減衰防止装置

振り子の構造を工夫しても、振り子の振幅の減衰は避けることができない。科学館の展示などで、長時間にわたり振り子を動作させるためには、数時間おきに振り直す必要がある。この問題を回避するため、主に電磁石による減衰防止装置が設置されている場合がある。

レオン・フーコーは、1855年に、フランスで初めて開催されたパリ万国博覧会の産業館において、フーコーの振り子の実験装置を用意した。ここで使用された振り子は、減衰に対し、電磁石によるブースト装置を加えたものであった。

カリフォルニア科学アカデミーのフーコーの振り子には、弦の上端側（支持装置側）に電磁石を使った減衰防止装置が組み込まれている。これは、振り子の錘が振り下がり支点の真下に達するタイミング、すなわち床面に対して弦が垂直の状態になる直前のタイミングで電磁石を通電し、弦を微小量だけ上側に引っ張る。弦の上端側の片が電磁石に触れると通電が切れて、錘がわずかに落下することで加振する。

乃村工藝社やソニーは、振り子の支点の真下の床面内に電磁石を設置する特許を出願している。これは床面内に振り子の錘の検出器があり、錘の通過に合わせて電磁石によって錘を吸引することで、振り子を加振する。

シャロン環

「シャロン環（英: Charron ring）」とは振り子の楕円運動を防止するための正円のトーラス状の部品である。フランスの物理学者、シャロン（M. Charron）が1931年に発表した。

シャロン環は、弦の支点の直下の位置に設置し、環の直径は振り子の最大振幅より若干小さいサイズにする。振り子の錘を振動させると、弦が環の内側に軽く当たり、振り子の運動の振幅方向以外の成分を打ち消すことができる。これによって振り子の楕円運動を防止できる。

ただしシャロン環と弦が接触している間は、シャロン環と弦との接触点が支点となり、弦長が短くなる。このため厳密には振り子の振動周期が短くなる。また、シャロン環への衝突により振り子の振動の減衰がおきるため別途減衰防止の方法が必要となる。

観測装置

コスモカイシャ・バルセロナのフーコーの振り子。錘の先によってブロックが倒れることで振動面の回転を示している。

国立科学博物館のフーコーの振り子の目盛盤。振り子の振動面の変化により表示ランプが点灯する。

床面の振り子の可動域の円周上にピンやブロックを並べ、振り子の錘がこれらを倒すことで振動面の変位を示す方法が一般的である。

1851年、レオン・フーコーがパンテオンで実験したとき、錘の下部には鉄筆状のものが取り付けられた。一方、床面の振り子の可動域の端に砂を盛った土手を設け、鉄筆がこの土手をかすめることで振り子の振動面の変位を示すようにした。

日本の国立科学博物館にあるフーコーの振り子には、直径150cmの目盛盤があり、振動方向を検知する赤外センサとそれを表示する表示ランプが48組並んでおり、振動面の位置を表示できるようになっている。赤外線センサは発光部と受光部が1対になっており、錘の下の反射によって錘の通過を検知する。

起動装置

フーコーの振り子を始動させるとき、錘を支持点の真下を通るように錘を正確に振り下ろす必要がある。わずかでも横方向に初速度が生じると振り子の振動面に横揺れが生じ、楕円運動の原因となるためである。

レオン・フーコーがパンテオンで公開実験したとき、振り子の錘をロープで固定し、実験開始時にこれをマッチで火をつけ、焼き切ることで始動していた。

国立科学博物館のフーコーの振り子は電磁石による始動を行っている。これは錘の鉄輪を電磁石で吸引し、電磁石への電流を切ることで錘を振り下ろすものである。

フーコーの振り子の小型化

フーコーの振り子の性質上、精度の高い実験を行うためには長い弦と大きい質量の錘が必要となり、結果として装置が大型になる。

リチャード・クレインの振り子

アメリカの物理学者のH・リチャード・クレインは、1981年に弦の長さが70cmのフーコーの振り子を発表した。

錘の下端に永久磁石を埋め込み、振り子の下側の床に固定された永久磁石と電磁石を設置した。錘の磁石を検知して位置を推定し、位置に応じて床の電磁石をオン・オフすることで錘の吸引と押出を行う。この磁石の作動にシャロン環を加えて楕円運動の発生を抑え、振動の減衰を防止した。

クレインの設計したフーコーの振り子の弦の長さは70cm。地球の自転による振り子の振動面の回転の誤差は2%以内。クレインは自身の設計したフーコーの振り子を時計として自宅とオフィスの2ヶ所で使用し、約10年間の連続稼働を行った。

クレインはさらに、同様の改良によって弦の長さが15cm（5.9インチ）でもフーコーの振り子として動作したと報告している。

日本の事例

和歌山県立粉河高等学校の教諭であった生地富雄により、弦の長さ：76cm、錘の質量：150gの小型の振り子での試作実験が、1963年に報告されている。楕円運動の対策としてシャロン環を使用。振動の減衰対策として振り子の支点の直下に電磁石を置いて、錘を電磁石で吸引する方法をとった。振幅9cmで実験したところフーコーの正弦則から求めた理論値に対して誤差5.3%以内の結果が得られたと報告している。この研究に対して日本学生科学賞地学クラブ総理大臣賞が送られている。

福島県教育センターの渡辺専一は、小型の振り子として錘の先端に発光体を取り付け、床面に凹面鏡を置く構成を発表した。振り子が振動すると光が凹面鏡に反射し、振幅が増幅されて天井に投影できる。渡辺によれば一般的な天井高のある部屋で実験が可能で、弦の長さが1.7から1.8mの振り子でも振動面の回転が観測できるとしている。

装置メーカー

日本国内で市販されている小型のフーコーの振り子（藤橋城）

フーコーの振り子は世界各国の博物館、科学館、大学などの展示ディスプレイとして数多く設置されている。世界で100以上の導入実績があるのはカリフォルニア科学アカデミーの装置部門、およびその後継としてカリフォルニア科学アカデミーで装置製造に従事していたキャリー・ポンキオーネ（Cary Ponchione）が設立したAcademy Pendulum Salesである。Academy Pendulum Salesでは、錘や電磁石ブースターなどをセットにした振り子キットを製造販売している。日本では、葛飾区郷土と天文の博物館、姫路科学館などに導入した実績がある。

日本では、乃村工藝社や木村製作所が展示ディスプレイ用途のフーコーの振り子を扱っている。また理科実験の目的で島津理科などから小型のフーコーの振り子が市販されている。

歴史

前史

→「天動説」および「地動説」も参照

紀元前4世紀のプラトンやアリストテレスは地球は宇宙の中心にあるという信念をもち、プトレマイオスが天動説として体系化した。ローマカトリック教会は聖書の解釈にプトレマイオスの天動説を利用した。

ニコラウス・コペルニクスはプトレマイオスの「アルマゲスト」を丹念に読み込み、自ら天体観測も行い、その修正を試みた。1540年、コペルニクスは自身の死を前に「天体の回転について」を出版し、その中で地球が他の惑星と同様に太陽の周りを公転するモデルを示した。しかし、ローマカトリック教会は、地球が動いているというコペルニクスの説は聖書の解釈と相容れないと判断した。

ガリレオ・ガリレイは自身で望遠鏡をつくり、天体観測を行った。ガリレオは木星を周回する衛星を発見し、その運行を記録した。木星を周回する衛星の発見は、ガリレオに太陽中心の地動説を確信へと導いた。ガリレオはローマに呼び出され裁判にかけられることになったが、ガリレオは論破できると考えていた。ガリレオは地動説を示す証拠として、海の潮汐現象を考えていた。しかし、1633年に有罪の判決を受けた。判決の内容は、地動説の破棄と自宅への幽閉などであった。

一方、ガリレオは単振り子の周期が錘の質量の大小によらず弦の長さに依存する「振り子の等時性」を発見していた。またガリレオの助手であったヴィンチェンツォ・ヴィヴィアーニは「単振り子の振動は、最初の垂直面から必ず同じ方向へずれていく」現象を1660年か1661年には記録していた。

マラン・メルセンヌによる、砲弾垂直打ち上げ実験を描いた絵。

ルネ・デカルトはガリレオの地動説を支持しつつも、教会からの異端審問を恐れ、オランダで隠遁生活を送っていた。デカルトは、大砲から放たれた砲弾の落下を観測すれば、地球の自転が証明できるはずだと考えた。デカルトは、文通で数学や哲学の議論を深めていたフランスの修道士のマラン・メルセンヌに大砲による実験を依頼した。

1638年の春、メルセンヌは助手と2人で大砲を使った実験に取り組んだ。大砲を垂直に向けて真上に砲弾を打ち上げた。1発目は行方不明。2発目は西に600mの地点に、3発目は東に600mの地点にそれぞれ着地。自分たちの頭上に砲弾が落ちてくる可能性がでてきたため、実験は中止となった。

アイザック・ニュートンは「落下するりんご」の話でシンボリックに語られる万有引力の発見で知られるが、またニュートンは地球の自転の証明に重力が使えるのではないかとも考えていた。1679年、ニュートンは「物体の落下は地球の自転（と慣性の法則）のために、落下地点が必ず東にずれるはずだ」というアイデアをロンドンの王立協会に手紙で送付した。ニュートン自身は実験を行わなかったが、ロバート・フックが提案に従って物体の落下実験を行った。フックの実験では「南東へのわずかなずれ」を観察したが、実験ごとの測定値のずれが大きく、地球の自転の証明とはならなかった。

地動説の決定的な証拠として年周視差の検出が考えられた。イギリスの天文学者のジェームズ・ブラッドリーは年周視差の検出を目的とし、1725年頃よりりゅう座ガンマ星の観測を始めた。この観測で年周視差の予想とは異なる観測結果を得た。ブラッドリーは熟考の末、観測結果から年周光行差を発見した。この光行差の予期せぬ発見は、地動説の証明となった。

自由落下のずれによる地球の自転の証明は、ドイツのヨハン・ベンツェンベルクとフェルディナント・ライヒによってそれぞれ独立に観測された。ヨハン・ベンツェンベルクは1802年からハンブルクの聖ミハエル教会、その後、ルール地方の石炭鉱山の竪坑において実験を行い、理論値より誤差を含むが明確な東側へのずれを観測し、1804年に論文を発表した。フェルディナント・ライヒは、フライベルク近郊の鉱山の竪坑で実験を行い、ほぼ理論通りの実験結果を得て、1831年に論文を発表している。

フーコーの着想

レオン・フーコー（1819年 - 1868年）

1819年、パリに生まれたレオン・フーコーは医者を志し医学校に通っていたが、次第にルイ・ダゲールの写真技術「ダゲレオタイプ」に強い関心を持つようになった。やはり元医学生であったアルマン・フィゾーと協力してダゲレオタイプの改良を行った。1845年にはフーコーとフィゾーは鮮明な太陽の写真撮影に成功した。その後、光の速度の測定を2人で始めるが、装置の方針を巡って喧嘩別れとなり、フーコーは単独で研究を続けることになった。

フーコーは理論家というより、自らの手で実験装置を作っていた技術者であった。フーコーは、望遠鏡の制御に使用する振り子時計の改良を行っていた。このとき、たまたま旋盤のチャックに装着されていた金属棒を振動させて、旋盤をゆっくり回しても振動面が変化しないことを見つけた。次に、フーコーはピアノ線に錘をつけた振り子をボール盤の台に取り付け、台をゆっくり回転させた。やはり、振り子の振動面は変化しないことを確認した。

フーコーは、旋盤やボール盤の回転台を自転する地球に置き換えれば、自転の影響で振り子の振動面の変化が観測できるはずだと考えた。ただし振り子の位置は平面上でなく球面上にあり、振り子が極点から赤道の間のどの位置にくるかによって振動面の運動は変化することに気がついた。この関係について「フーコーの正弦則」と呼ぶが、フーコーは力学理論の素養なしに、直感的に導き出した。

最初の実験

かつてフーコーの自宅のあったパリ、ヴォージラール通りとアッサス通りとの交差点にある建物の側壁レリーフ（位置：北緯48度50分52.02秒 東経2度19分47.16秒）。フーコーの略歴が刻まれている

フーコーは本物の振り子を使って、正弦則を目で確認できないかと考えた。長さ2mの鋼鉄製ワイヤーの一端を自宅の地下室の天井からつり下げ、しかも、ねじれることがないように工夫した。錘として5kgの真鍮製のものが取り付けられた。振り子がなんの干渉も受けずにあらゆる方向に揺れることができるようになるまで、およそ1ヶ月の試行錯誤が必要であった。

1851年1月3日、実験を開始したがすぐにワイヤーが切れた。数日後、再び実験を行った。フーコーは、実験開始から1時間後には「目に見えて位置の変化が起こる」こと、「振り子は天球の日周運動と同じ向きに回転する」ことを観察した。

パリ天文台での実験

フーコーは、パリ天文台の台長であったフランソワ・アラゴに公開実験を申し出た。アラゴは申し出を受けいれ、フーコーはただちに準備に取りかかった。実験場所はパリ天文台の中央ホールである「子午線ホール」となった。錘は自宅での実験と同じもの（5kg）を、弦は長さ11mのワイヤーに変更した。

フーコーはパリ在住の科学者に以下の内容の招待状を送った。

Vous êtes invités à venir voir tourner la Terre, dans la salle méridienne de l Observatoire de Paris.

（地球の自転を見に来られたし、パリ天文台の子午線ホールにて。）

1851年2月3日、多くの科学者たちがパリ天文台に集まり、実験に立ち会った。またフーコーは同日、科学アカデミーに対して、自宅の地下室で行った実験の結果と地球の自転の証明に関する論文を報告した。この中で「フーコーの正弦則」を使い、振り子のある緯度と振り子の振動面の関係について明らかにした。

フーコーの実験は驚きをもって迎えられた一方で、招かれた科学者たちには「フーコーの正弦則」に目新しい点は無いという考え方が多数派であった。例えば、1851年3月16日、ジョヴァンニ・プラーナは「（フーコーの正弦則は）1837年にシメオン・ドニ・ポアソンが発表した論文「投射物の運動について」において、「（フーコーの振り子の現象は）すでに予測された範囲である」との論文を投稿した。ポアソンは大砲から打ち出された弾は、地球の自転により、わずかに横にずれるはずだと考え理論式を構築していた。またポワソンは地球の自転が振り子にも影響を及ぼすが、観察することは困難だと考えていた。

パンテオンでの公開実験

フランスの大統領であったルイ・ナポレオン（のちに皇帝ナポレオン3世）はパリ天文台でのフーコーの実験を耳にし、パンテオンでの公開実験を命じた。フーコーは、新たに振り子を準備し、錘は真鍮製で28kg、直径38cmの球体のものを作らせた。弦は、パンテオンのホールの天井の高さに合わせて、長さ67mのものを用意した。また錘の下部には鉄筆状のものが取り付けられた。この工夫により、振り子の可動域の端に砂を盛った土手を設け、鉄筆が土手をかすめることで振り子の位置の変位を示すようにした。

1851年3月27日、ルイ・ナポレオンの臨席のもと、パリ市民の前で、パンテオンでの公開実験が行われた。振り子の実験は完璧ではなく、時間経過すると軌道が8の字運動になり振幅も減衰を始めたが、数時間経過すると、目に見えて振動面が変化が観察できた。ルイ・ナポレオンは実験に満足し、1854年にフーコーをパリ天文台付きの物理学者に任命した。

その後、パンテオンでの実験は毎週木曜日に実施された。しかし、1851年12月1日、ルイ・ナポレオンは「パンテオンでの実験をただちに終了し、パンテオンを教会としての役目に戻せ」という大統領令を出し、公開実験は終了した。

各地での再現実験

1851年5月8日、ランスのノートルダム大聖堂で振り子の実験が行われた。イタリアでは、アンジェロ・セッキがローマの聖イグナチオ教会のドームで振り子の実験を行った。また同じ年に、イギリスのオックスフォード大学ラドクリフ・カメラ、ドイツのケルン大聖堂、ジュネーヴ、ダブリン、ニューヨークでも実験が行われた。

1851年の9月から10月にかけて、南半球のリオデジャネイロで再現実験が行われた。振り子は弦の長さが4.37m、錘の質量が10.5kgで約2ヶ月間行われた。この実験結果はフランス科学アカデミーに報告された。

1855年、フランスで初めて開催されたパリ万国博覧会の産業館において、フーコーの振り子の実験が行われた。この振り子はフーコー自身が準備し、新たに振り子の振動の減衰に対して、電磁石によるブースト装置を加えたものであった。

50年記念実験

1902年、フーコーの実験をパンテオンで再現したときの写真。左がカミーユ・フラマリオン。

1902年、天文学者のカミーユ・フラマリオンは、最初のフーコーの振り子の実験から半世紀を記念し、フランス天文学協会に対して再びパンテオンでの公開実験を提案した。フランス天文学協会の会長はアンリ・ポアンカレであり、フラマリオンの提案に同意した。

1902年10月22日、パリのパンテオンに作曲家のカミーユ・サン＝サーンス、彫刻家のオーギュスト・ロダン、同じく彫刻家で自由の女神像を製作したフレデリク・バルトルディなどの招待客を含め、観衆が2000人以上集まった。午後2時、公共教育大臣のジョセフ・ショーミエが錘を固定しているロープを火で焼き切って、実験を開始した。そして、フラマリオンが以下のようにスピーチを行った。

一般向けの天文学に関してこれまでになされた公開実験の中で最も壮大なものは、間違いなくレオン・フーコーが半世紀前にこの場所で行った印象に残る実験である。この実験は、この地球の自転運動を具体的に明快かつ壮麗に証明し、惑星すなわち「移動する星」という言葉がわれわれの住む世界にふさわしいことを、文字どおり断定したのである。 —  カミーユ・フラマリオン

日本でのフーコーの振り子

東京科学博物館にフーコー振り子が設置されたことを報じる新聞記事（東京読売新聞1934年4月22日夕刊）。

「談天」は、漢籍本「譚天」に訓点を施した本で、西洋天文学を紹介したものである。原著者は、候失勒（ジョン・ハーシェルのこと）で1851年に刊行された「Outlines of Astronomy(天文学概要)」を、英国人の偉烈亜力（Alexander Wylie）が口語訳し、清国人の李善蘭が漢訳して、1859年に出版された。これに福田理軒が訓点を施し、上中下の3冊が1861年（文久元年）に刊行された。「談天」の二篇には、地球の自転に関する説明があり、その中でフーコーの振り子の実験の記述がある。

「東洋学芸雑誌」第25号（1883年10月発行）に掲載された菊池大麓が著した「地動說ノ証據」の中で、地球の自転に関する解説がある。この解説では、地球の自転を示す証拠としてフーコーの振り子とジャイロスコープが説明されている。またこの解説には、東京大学でフーコーの振り子の実験を行ったことについて簡単な記述がある。このとき使用された振り子は、弦が長さ16から17尺（約4.8から約5.2m）の銅線、錘の重さが11貫目（約41kg）、錘の直径が7寸（約21cm）であった。

1932年の天文学術誌「天界」に広島文理科大学の中村饒がフーコーの振り子の実験方法の改良について記事を投稿した。中村は、振り子の錘に豆電球を取り付け、これを発光させながら振り子を振動させ、下面から写真機を長時間露光することで振動面の回転を記録するというものであった。

1934年4月21日に東京科学博物館上野新館（現：国立科学博物館日本館）に設置された。常設展示としては日本初である。

世界各地のフーコーの振り子

国際連合本部ビルのロビーにあるフーコーの振り子

→詳細は「フーコーの振り子のある施設の一覧」を参照

フーコーの振り子は、「地球の自転の証明」という科学教育の観点から、世界中の博物館、科学館、学校などに数多く設置されている。

ニューヨークにある国際連合本部ビルのロビーの大階段には、弦長が約23m、錘の質量が約91kgのフーコーの振り子が存在する。1955年にオランダが寄贈したもので、ユリアナ女王のメッセージが刻まれている。

日本では、1934年4月21日に国立科学博物館に常設展示された。また、東京ディズニーシーのフォートレス・エクスプロレーションの中にフーコーの振り子がある。

オリジナルのフーコーの振り子

フーコーがパンテオンで1851年に実験した振り子の錘は、フランス国立工芸院附属のパリ工芸博物館に展示されている。またフーコーが公開実験を行ったパンテオンのドームにはフーコーの振り子が取り付けられ、実際に動いている。現在パンテオンの振り子の錘は、パリ工芸博物館の実物を複製したものである。

世界最大・世界最長のフーコーの振り子

聖イサアク大聖堂のドームに存在したフーコーの振り子（1985年）

アメリカ合衆国オレゴン州ポートランドのオレゴン・コンベンション・センター にあるフーコーの振り子は、弦の長さが約21m（70フィート）、錘の質量が約340kg（750ポンド）であり、錘の質量では世界最大を自称している。

ソビエト連邦時代、サンクトペテルブルクの聖イサアク大聖堂のドームにフーコーの振り子が設置されていた。当時、聖イサアク大聖堂は宗教利用を禁じられ博物館として利用されていた。大聖堂のドーム高は約100m。取り付けられた振り子の弦もドーム高に合わせて98mあり、恐らく世界で最も長い弦長をもつフーコーの振り子であった。

ラトビアの首都リガにあるリガ・ラジオ・アンド・テレビ・タワーは、再開発プロジェクトに合わせて2019年より改装工事を行っている 。リニューアル時に、塔を支える脚の間に、弦の長さが70m以上、錘の重量500kgのフーコーの振り子が設置されることになっている。竣工予定は2023年から2024年頃で、「完成すれば世界最大で最長のフーコーの振り子となる予定」と主張している。

南極点での実験

「フーコーの正弦則」によると、極点でフーコーの振り子を実験すると振動面が1時間ごとに15度移動、24時間で1回転する。これを実験で確認するために、2001年、ソノマ州立大学のA. ベイカーらが南極点にあるアムンゼン・スコット基地でフーコーの振り子の実験を行った。実験場所は建設中の建物の階段の吹き抜けで、実験時の気温は-67度であった。また大気圧が660hPaで、海抜約3,350m相当の場所であった。

実験で使用した振り子は、弦の長さ33m、錘の質量が25kgを使用した。計測した振り子の周期は11.5秒であった。実験は20分間行い、計算通り振動面の5度の回転を観測した。

レオン・フーコー以後の研究

ホイートストンの装置

チャールズ・ホイートストンによる「ばね」を使ったフーコーの振り子の原理を説明するための装置

イギリスの物理学者、チャールズ・ホイートストンは、レオン・フーコーによる振り子を使った地球の自転の証明方法についての補足を1851年に発表した。フーコーの振り子が地球の自転の証明であることへの根本的な疑い、および観察地点の緯度により振動面の回転速度が異なるという「フーコーの正弦則」の説明の難解な点に応えた内容であった。この論文の中でホイートストンは、「ばね」を使った装置を提示した。

装置は、円形のターンテーブルに、半円形のアーチ状のスライダーがターンテーブルの直径方向にままたぐように取り付けられている。ばねはスライダーとターンテーブルの中心点の間を接続するように取り付けられている。バネを横方向に引っ張ると振動し、振動面がターンテーブルを回したときの状況を観察できる。

ばねがターンテーブルの面に対して垂直に立っているとき、ばねを横振動させてターンテーブルを回転させ、ターンテーブルの直上から観察すると、ターンテーブルが回っていても振動面は変化しない。ターンテーブル上にある視点から見ると、ばねの振動面はターンテーブルの回転速度と同じ速度で、ターンテーブルの向きとは逆の向きで回転しているように見える。これは極点でのフーコーの振り子の動作に一致する。

ばねとターンテーブルのなす角を任意の角度（ただし0度ではない）に設定し、ターンテーブルを回転させてターンテーブルの直上から見ると、ばねの振動面が回転することを観察できる。例えば、ばねを30度に設定すると、ターンテーブルを2回転させると振動面が1回転する。同様に、ばねを19.5度に設定してターンテーブルを3回転させると振動面が1回転、ばねを14.5度に設定してターンテーブルを4回転させると振動面が1回転する。つまり、ばねとターンテーブルのなす角度は、フーコーの振り子における実験地点の緯度に相当する。

オネスによるフーコーの振り子の研究

ヘイケ・カメルリング・オネスが使用したフーコーの振り子の概念図（Fig.1）。全体を金属ケースで密封し、0.1気圧以下に減圧して実験を行った。

ヘイケ・カメルリング・オネスの論文で示されたフーコーの振り子の軌道。リサジュー図形のように楕円軌道が変形している。

オランダの物理学者、ヘイケ・カメルリング・オネスはヘリウムの液化や超伝導の発見など低温物理学の分野に業績があり、1913年にはノーベル物理学賞を受賞した人物である。オネスは、フローニンゲン大学で1879年に博士号を取得したが、博士論文のタイトルは「蘭: Nieuwe bewijzen voor de aswenteling der aarde（地球の自転の新たな証拠）」で、フーコーの振り子の現象の一般化（レオン・フーコーが示した地球の自転による振り子の振動面の回転は特殊な振り子であること）を示した研究であった。

オネスにフーコーの振り子の研究を勧めたのはグスタフ・キルヒホフであった。キルヒホフはフーコーの振り子について、数学モデルと実験結果が示す差異に不満を持っていた。オネスは、1872年の秋からフーコーの振り子の実験に取り組み、一時中断した後、1876年の春に博士論文のテーマとした。

オネスが実験に使用した振り子は、弦が1.2mの細い銅管で、錘が質量15kgの鉛の球を使った。支持装置は板バネ付きのダブルナイフエッジを使用した。また空気抵抗を無視できるようにするため、振り子全体を金属ケースで囲み、減圧して0.1気圧以下で実験を行った。

また錘の軌道は、振り子に取り付けられた鏡と、プリズムとレンズの組み合わせで光学的に観察するにようになっていた。振り子の鏡で反射された光は、金属ケースのガラス窓を通して装置外部に出力され、これを拡大レンズを通して観察した。接眼レンズには目盛が刻まれており、振り子の振動面の角度と振幅を正確に記録できた。

このように外乱を可能な限り排除し、地球の自転が振り子の軌道に与える影響を観察したが、時間が経過すると錘の運動が楕円になる現象が生じた。オネスは装置の改良と実験を重ね、2年の歳月を費やしたが、振り子の軌道が楕円になる現象は解消されなかった。オネスは実験結果と理論面を見直し、振り子の楕円軌道によっても振動面の回転が起きると考え方を改めた。

理想的な振り子の弦の支点は、どの方向に錘を振動させても一点で固定されていると仮定する。しかし、現実には機械的制約により縦方向（便宜的に$x$軸方向）と横方向（$y$軸方向）の支点位置がわずかにずれ、$x$軸方向で振動している時の弦長$l_{x}$と$y$軸方向で振動している時の弦長$l_{y}$が異なることになる。従って、振り子の運動方程式は

$F_{x}\simeq -{\frac {mgx}{l_{x}}}$

$F_{y}\simeq -{\frac {mgy}{l_{y}}}$

$x$軸方向の振動周波数（$\psi _{x}$）と$y$軸方向の振動周波数（$\psi _{y}$）が異なる原因となる。

$\psi _{x}={\sqrt {\frac {g}{l_{x}}}}$

$\psi _{y}={\sqrt {\frac {g}{l_{y}}}}$

弦の長い振り子では$x$軸と$y$軸の振動周波数の違いは無視できるが、弦の短いフーコーの振り子では深刻な問題となる。オネスの数学モデルと実験結果から、$x$軸と$y$軸の振動周波数が違なる場合、地球の自転により振動面が回転すると、初動時に直線運動であっても、時間が経過すると楕円軌道となる。$x$軸と$y$軸の振動周波数の違いにより、地球が自転していなくても振動面が徐々に回転する。この現象を球面振り子の楕円運動による面積効果と呼ぶ。つまり楕円軌道を描く錘の軌跡は、周波数$\psi _{x}$と$\psi _{y}$のリサジュー図形になる（ハーモノグラフも参照）。

理想的なフーコーの振り子は、振動が直線のまま、長時間にわたり振動面の回転が観察できることである。これを満たすためには、$x$軸と$y$軸の振動周波数が等しく、$x$軸と$y$軸の慣性モーメントも等しい、「完全対称」な振り子が必要となる。

コンプトン・ジェネレーター

→詳細は「コンプトン・ジェネレーター」を参照

コンプトン・ジェネレーターを使い、地球の自転を観察している様子

アメリカ合衆国の物理学者であるアーサー・コンプトンはコンプトン効果を発見し、1927年にノーベル物理学賞を受賞した人物である。コンプトン・ジェネレーターとは、アーサー・コンプトンがウースター大学の学生であった1913年に発表した地球の自転を観測する装置である。

装置の形状は、トーラス状の中空管になっている。リング管の内側は水で満たされていて、流速を計測できるようになっている。コンプトンは水に少量の油を混ぜて油球をつくり、これを顕微鏡を使って流速を測定した。またトーラスの管は、直径方向に回転軸がついておりリング面を反転することができる。

実験は、まずリング面を水平にして回転軸を東西方向になるように設置する。リング管の中の水が静止した状態から、ゆっくり（約3秒程度で）180度回転してリング面を反転させて、リング管の中の流速を測定する。

ここでリングの半径を$R$、地球の自転の角速度を$\omega$、リングの置かれた位置の緯度を$\theta$とし、リング面が水平で静止した状態から反転させたときの流速を$v_{th}$とすると、理論値は以下のように求めることができる。

$v_{th}=2\omega R\sin \theta$

この計算方法に従うと、東京（北緯35度）で半径50cmのコンプトン・ジェネレーターを水平から180度反転させて流速を測定すると、0.04 mm/s（分速2.5mm）となる。コンプトンの実験結果は、理論値から3%以内の誤差に収まったことが報告されている。

レンズ・サーリング効果

→「慣性系の引きずり」も参照

「レンズ・サーリング効果」とは、大質量物体（例えば地球）が回転するの近くにある慣性空間を引きずること現象のことである。例えば、広げた布の上にボールを置き、これを布の上で回転させると布が回転に引っ張られるが、同様に地球の自転によっても発生し、結果としてフーコーの振り子の振動面の回転に歳差運動が生じると考えられる。これは一般相対性理論により予言された。

1984年、ロシアの物理学者のウラジーミル・ブラジンスキーは、「レンズ・サーリング効果」の検出のため、南極点にフーコーの振り子の建設を提案した。これを受けてイギリスの物理学者のブライアン・ピパードは、「レンズ・サーリング効果」の検出を目指したフーコーの振り子を製作したが、製作した振り子を極点に設置しても検出は困難であることを1988年に報告している。このとき、ピパードの作成したフーコーの振り子は、ロンドンのサイエンス・ミュージアムに展示されている。

アレ効果

パラコニカル振り子による観測を行うモーリス・アレ。

1988年にノーベル経済学賞を受賞したモーリス・アレであるが、物理学にも強い関心を持っていた。「アレ効果」とはモーリス・アレが観測した、日食の際にフーコーの振り子の振動面の回転異常が生じる現象である。アレはこの現象を一般相対性理論では説明できないと主張したが、現象の存在そのものを含めて未解決問題である。

1954年、アレがサン＝ジェルマン＝アン＝レーで、6月9日から7月9日までの間、フーコーの振り子の連続観測を行っていた。観測中の1954年6月30日の日食において日食の始まりと日食の終わりで、振り子の振動面の急激な回転を観察したと報告している。

アレは1959年、振り子の支点が平面に加えて弦の回転方向についても自由度を持つ3自由度の振り子である「パラコニカル振り子」を使った実験を行った。1959年10月2日の日食においても、アレは振動面の回転異常を観察した。

1999年8月11日の日食はヨーロッパを横断する皆既日食であったが、NASAマーシャル宇宙飛行センターのD.NoeverとR.Koczorを中心に「アレ効果」を世界各地で観察を行った。アメリカ合衆国、オーストリア、ドイツなど7ヵ国でフーコーの振り子および重力計を使って測定が行われた。この観測の結果では、通常とは異なるデータが観測された所もあるが、何らかの測定誤差の範囲を出ないと否定的な結論となった。このレポートについてモーリス・アレは、「実験時間が短い」などの反論を行っている。

工学への影響

ジャイロスコープ

フーコーが製作したジャイロスコープ。右に観測用の顕微鏡。

レオン・フーコーは、振り子の実験ついて数学者のルイ・ポワンソーとの間で議論を交わし、その中で振り子の代わりに回転する物体を使えばより小型な装置で地球の自転を観測できることに考えが至った。回転体（ローター）として真鍮製のトーラスの中心に金属円盤を取り付け、軸を貫通させたものであった。この回転体をジンバルで固定した。フーコーは「回転を見る」というラテン語から「ジャイロスコープ」と命名した。

ジャイロスコープは専用の起動装置を使って、回転体に高速の回転を与える必要があった。起動時に特定の方向に回転体は姿勢を保つが、時間が経過すると地球の自転と共に回転体の向きが移動するように見えた。フーコーの製作したジャイロスコープは、10分程度しか回転体（ローター）の回転が持続しなかった。このため、地球の自転の影響を観測するためには顕微鏡を用いた。

実際には、ドイツの数学者のヨハン・ボーネンベルガーが、1817年に回転体として球体を使ったジャイロスコープを論文とし投稿しており、ボーネンベルガーの作成した装置自体はそれ以前から存在していた。フランスの数学者、ピエール＝シモン・ラプラスやシメオン・ドニ・ポアソンはボーネンベルガーの装置について存在を知っていた。特にポアソンは1813年の回転体の動力学の解析に関する論文の中でボーネンベルガーの装置を使った説明を行っている。従って、フーコーのジャイロスコープはボーネンベルガーの装置をベースとして改良したものだと推定されている。

MEMSジャイロセンサー

プルーフマス（英: Proof mass）の概念

スマートフォンやデジタルカメラなどに、本体の姿勢を検知するためにジャイロセンサーを内蔵した電子機器が数多く存在している。これらジャイロセンサーは振動型ジャイロスコープと呼ばれる種類が一般的で、半導体集積回路の製造技術から発展したMEMSと呼ばれる技術によって作りだされた。MEMSジャイロスコープは、角速度を出力するため回転角を取得するためには出力信号を積分する必要がある。しかし角速度信号は不安定で、これを積分すると経過時間と共に誤差が蓄積する現象（ドリフト現象）が発生することが知られている。

一方、「フーコーの振り子」は、ゆっくりとした地球の回転を測定できる高性能な積分ジャイロセンサーとみなすこともできる。フーコーの振り子を半導体チップ上に実現したデバイスを「全角度モード・ジャイロスコープ（英: Whole angle mode gyroscope）」と呼ぶ。例えば2011年に、カリフォルニア大学アーバイン校のマイクロシステム研究室は、MEMS技術を応用して半導体マイクロチップの上に「フーコーの振り子」を作ることに成功したと発表した。

「全角度モード・ジャイロスコープ」には、弦と錘の単振り子が入っているわけではなく、「プルーフマス（英: Proof mass、試験質量）」と呼ばれるものが使われている。これは試験質量を$x$軸、$y$軸に沿った方向にバネで支持して振動させ、各軸の変位を観測することで角速度を検出する。「全角度モード・ジャイロスコープ」はさらに、$x$軸方向と$y$軸方向の振動を完全対称（周波数、振幅、Q値などを同一）にすると、試験質量にはコリオリ力が働き、フーコーの振り子と同じく振動面が回転する。

カリフォルニア大学アーバイン校のマイクロシステム研究室が作成したものは、4つの「プルーフマス」を使用した全角度モード・ジャイロスコープである。彼らの主張によると、事実上入力角度の範囲は無制限で、ドリフト現象も1時間あたり0.5度以下に抑えられたとしている。

その他の影響

小説

イギリスの小説家のキャサリン・エアードが、1981年に発表したミステリー小説「His Burial too（邦題：そして死の鐘が鳴る）」では、フーコーの振り子が事件の重要な鍵となっている。

イタリアの哲学者、ウンベルト・エーコは1988年初出の小説に「フーコーの振り子」のタイトルをつけた。物語は、登場人物の一人がフーコーの振り子が展示されたパリ工芸博物館で閉館後に出来事を振り返る形で語り始める。内容は物理学とは無関係であるが、主人公ら3人がでっち上げた架空の陰謀論と古代伝承が次第にリンクしていき、振り子のように揺れ動く物語となっている。

芸術作品

ニューヨークブロンクスのモンテフィオーレ・メディカル・センター内の小児病院のロビーにあるフーコーの振り子は、パブリック・アーティストのトム・オターネスがデザインした「帽子を被った錘」になっている。

ドイツの画家であるゲルハルト・リヒターは、2018年、ミュンスターにあるドミニカ教会にフーコーの振り子をつかったインスタレーションを寄贈した。作品名は「Zwei Graue Doppelspiegel für ein Pendel（振り子のための2組の灰色の合わせ鏡）」である。

日本の前衛美術家の風倉匠は、1962年の読売アンデパンダン展にフーコーの振り子によるインスタレーションを出品した。これは会場の天井から吊るした7つのフーコーの振り子を用いたもので、振り子は自転の作用でわずかに動く「ゼロ型のパフォーマンス」であった。また風倉は1971年に現代日本美術展へ「魔術によって宇宙の一部を証す道」と題したフーコーの振り子によるインスタレーションを出品した。振り子の振幅によって音色が変わる仕掛けであったが、会場の東京都美術館から振り子を吊るすことを拒否されたため、床に錘を置いたままの展示となった。

展示物としてのフーコーの振り子

世界各地の博物館などにフーコーの振り子が展示されているが、科学史を専門とするロバート・クリースは、自著で「フーコーの振り子」を「もっとも美しい10の科学実験（The Ten Most Beautiful Experiments in Science）」の1つに選び、これらの展示について以下のように述べている。

フーコーの振り子は、博物館の他の展示物とはだいぶ趣が異なっている。（中略）振り子は、光が出るわけでも、音が鳴るわけでもなく、ただ静かに、厳粛に、荘重に動くだけだ。とりわけ重要なのは、振り子はただ単にインタラクティブではないというレベルを越えて、われわれを完全に無視し、人間的な経験から考えれば根本的に直感に反する事実を露わにしているように見えることだ。 —  Robert P. Crease 、世界でもっとも美しい10の科学実験

参考文献

本記事で出典として使用している文献を、発表順に示す。

論文・解説

•  Léon Foucault (1851) (フランス語), Démonstration physique du mouvement de rotation de la Terre au moyen du pendule, ウィキソースより閲覧。 
•  Charles Wheatstone (1851) (英語), Note relating to M. Foucault's new mechanical proof of the Rotation of the Earth, ウィキソースより閲覧。 
• 菊池大麓「地動說ノ証據」『東洋學藝雜誌』第25巻、東洋學藝社、1883年10月、157-161頁、全国書誌番号:00017007。 
• 中村 饒「フーコーの振子を用ひて地球の自轉角の寫眞を撮る裝置」『天界』第5巻第134号、天文同好會、1932年、206-210頁、NAID 120004945287。 
• 鈴木 敬信「地球の自転とフーコー振子」『自然科学と博物館』第5巻第5号、東京科学博物館、1934年、6-14頁、NCID BB28488798。 
• 鈴木 敬信「地球の自転とフーコー振子(完)」『自然科学と博物館』第5巻第7号、東京科学博物館、1934年、6-10頁、NCID BB28488798。 
• P.E. Wylie「The Paradox of Foucault Pendulum」『天界』第33巻第337号、東亜天文学会、1955年9月、226-229頁。 
• 岡山 誠司「フーコーの振子が意味するもの」『科学の実験』第10巻第1号、共立出版、1959年1月、22-27頁、NCID AN0036555。 
• 岡山 誠司「フーコーの振子が意味するもの(下)」『科学の実験』第10巻第3号、共立出版、1959年3月、51-58頁、NCID AN0036555。 
• 生地 富雄「フーコーの振子の実験」『科学の実験』第14巻第8号、共立出版、1963年7月、36-47頁、NCID AN0036555。 
• 佐藤 明達「フーコー振子の誤解」『科学の実験』第17巻第2号、共立出版、1966年7月、74-79頁、NCID AN0036555。 
• 村内 必典、浅沼 俊夫「国立科学博物館のフーコー振り子の構造と改良」『自然科学と博物館』第37巻、国立科学博物館、1970年、42-55頁、NAID 40017859802。 
• 渡辺 専一「フーコー振り子による測定の新方法」『科学の実験』第24巻第3号、共立出版、1973年3月、91-92頁、NCID AN0036555。 
• 玉木 英彦「中緯度のフーコー振り子の振動面はなぜ24時間で1回転しないか」『数学セミナー』第20巻第9号、日本評論社、1981年9月、35-40頁、NCID AN10333470。 
• 佐々木 勝浩「国立科学博物館のフーコー振り子の改良について」『国立科学博物館研究報告』第4巻、国立科学博物館、1981年、31-40頁、NAID 110004312216。 
• H. Richard. CRANE (1981). Short Foucault pendulum: a way to eliminate the precession due to ellipticity. 49. pp. 1004-1006. 
• V.B. Braginsky (1984). “Foucault pendulum at the South Pole: proposal for an experiment to detect the Earth's general relativistic gravitomagnetic field”. Physical Review Letters 53 (9): 863-866. 
• 矢野 淳滋「フーコーの振り子を教えるための振り子（特別企画）」『物理教育』第34巻第1号、日本物理教育学会、1986年、27-32頁。 
• 長谷田 秦一郎「フーコーの振り子」『科学』第57巻第1号、岩波書店、1987年1月、44-47頁、NCID AN00036810。 
• A.B. Pippard (1988). “The parametrically maintained Foucault pendulum and its perturbations”. Mathematical and Physical Sciences 420 (1858): 81-91. 
• 伊多波 正徳「フーコー振子の特性とその改良に関する研究」『茨城大学工学部研究集報』第40巻、茨城大学工学部、1992年、247-252頁。 
• 宮坂 忠昭「フーコー振子の簡単な説明法」『長野工業高等専門学校紀要』第28巻、長野工業高等専門学校、1994年、75-80頁、NAID 120005275107。 
• H. Richard. Crane (1995). “Foucault pendulum ‘‘wall clock’’”. American Journal of Physics 63 (1): 33-39. 
• 佐野画廊 編『時計の振子、風倉匠』佐野画廊、1996年。ISBN 4879953792。 NCID BA69922876。 
• Maurice Allais (1999). “The ‘Allais Effect’and My Experiments With the Paraconical Pendulum 1954–1960” (pdf). A memoir prepared for NASA. http://www.allais.info/alltrans/nasareport.pdf. 
• John Oprea (1999). “Geometry and the Foucault pendulum”. The American mathematical monthly (Isis) 102 (6): 515-522. 
• “The Foucault Pendulum at the California Academy of Sciences:A Guide for Docents”. CALIFORNIA ACADEMY OF SCIENCES: 1-6. (2010). 
• Jörg F. WAGNER (2010). “The machine of Bohnenberger”. The History of Theoretical, Material and Computational Mechanics-Mathematics Meets Mechanics and Engineering (Springer): 81-100. 
• 室谷 心「フーコーの振り子の回転角を工作で求める(私の工夫)」『物理教育』第28巻、日本物理教育学会、2011年、118-119頁、NAID 120005275107。 
• Prikhodko, Igor P.; Zotov, S. A.; Trusov, A. A.; Shkel, A. M. (2012). “Foucault pendulum on a chip: Rate integrating silicon MEMS gyroscope.”. Sensors and Actuators A: Physical (IEEE) 177: 67-78. 
• 中尾 政之「だから、機械はおもしろい!(第36回)サプライズの科学 フーコーの振り子」『機械設計』第54巻第7号、日刊工業新聞社、2013年、78-80頁、NAID 40019612972。 
• 廣瀬 匠「星の都の物語(第2回)地球の自転を刻むアート」『月刊星ナビ』第17巻第8号、アストロアーツ、2016年、48-50頁、NCID AA11490406。 
• Joël Sommeria (2017). “Foucault and the rotation of the Earth”. Comptes Rendus Physique 18: 520-525. 
• 道下 敏則、髙橋 輝雄「自立型フーコー振子の最適運転」『人間・環境学』第27巻、京都大学大学院人間・環境学研究科、2018年、1-15頁、NAID 120006591387。 

書籍

• 国井 修二郎、千田 香苗『力学〈1〉』丸善〈エンジニアスライブラリ〉、1952年。 NCID BB07851073。 
• J.ウォーカー『ハテ・なぜだろうの物理学〈1〉』培風館、1979年。ISBN 4563020060。 
• 藤原邦男『物理学序論としての力学』東京大学出版〈基礎物理学〉、1984年。ISBN 9784130620710。 
• 近角聡信『日常の物理事典』東京堂出版、1994年。ISBN 4-490-10372-7。 
• Louis N. Hand; Janet D. Finch (1998). Analytical Mechanics. Cambridge University Press. ISBN 0521573270 
• Friedrich Dannemann 著、安田徳太郎 訳『新訳ダンネマン大自然科学史』 7巻、三省堂、2002年。ISBN 4385361061。 
• Friedrich Dannemann 著、安田徳太郎 訳『新訳ダンネマン大自然科学史』 9巻、三省堂、2002年。ISBN 4385361061。 
• William Tobin (2003). The life and science of Léon Foucault : the man who proved the earth rotates. Cambridge University Press. ISBN 0521808553. NCID BA64871814 
• Gregory L. Baker (2005). The Pendulum: A Case Study in Physics. Oxford University Press. ISBN 0198567545 
• Millard F. Beatty, Jr. (2006). 　Dynamics : the analysis of motion. Springer. ISBN 0387237046. NCID BA75387879 
• アミール・D. アクゼル 著、水谷 淳 訳『フーコーの振り子―科学を勝利に導いた世紀の大実験』早川書房、2005年。ISBN 978-415208680-8。 
• VAN DELFT, Dirk (2007). Freezing Physics: Hieke Kamerlingh Onnes and the Quest for Cold. Koninklijke Nederlandse Akademie van Wetenschappen 
• ロバート P. クリース 著、青木 薫 訳『世界でもっとも美しい10の科学実験』日経BP、2006年。ISBN 978-4822282875。 
• John Graham-Cumming (2009). The Geek Atlas: 128 Places Where Science and Technology Come Alive. O'Reilly Media. ISBN 978-0596523206 
• 中村 士、岡村 定矩『宇宙観5000年史』東京大学出版会、2011年。ISBN 978-4130637084。 
• 長谷川律雄『力学入門 : コマから宇宙船の姿勢制御まで』中央公論新社〈中央新書〉、2015年。ISBN 978-4121023544。 
• 近世歴史資料研究会 編『日本科學技術古典籍資料：天文學篇9』科学書院〈近世歴史資料集成 ; 第7期第8巻〉、2015年。ISBN 9784760304103。 NCID BB19395947。 
• 鈴木将『フーコーの振り子に魅せられて』丸善出版、2018年。ISBN 978-4863453890。 
• Gregory L. Baker (2018). Seven Tales of the Pendulum. Oxford University Press. ISBN 978-0198816904 

特許

• JP H08-86887A, "振り子装置と振り子の振幅制御方法", published 1996-04-02, assigned to ソニー 
• JP P2002-358001A, "振り子装置", published 2002-12-13, assigned to 乃村工藝社 

WEBサイト

• 中山 恵二 (1980年). “地球の自転に伴う地表の回転と緯度との関係を観察する教具”. 東レ科学振興会. 2019年10月23日閲覧。（日本語）
• R. Allan Baker (2001年). “South Pole Foucault Pendulum”. Sonoma State University. 2019年9月15日閲覧。（英語）
• “FOUCAULT PENDULUM”. United Nation. 2019年9月15日閲覧。（英語）
• “The world’s biggest Foucault pendulum”. Seattle Astronomy. 2019年9月15日閲覧。（英語）
• “Longest pendulum”. Guinness World Records. 2019年9月15日閲覧。（英語）
• “Heike Kamerlingh Onnes Facts”. THE NOBEL PRIZE. 2019年9月15日閲覧。（英語）
• “Decrypting the eclipse: A solar eclipse, global measurements and a mystery”. NASA. 2019年9月15日閲覧。（英語）
• “French Nobel Laureate turns back clock”. NASA (2011年7月26日). 2019年9月15日閲覧。（英語）
• “Made On Earth — Pendulum Perfector”. Make:. 2019年9月15日閲覧。（英語）
• “How to track the Earth’s rotation with a PlayStation Move controller”. WIRED (2011年2月23日). 2019年9月15日閲覧。（英語）
• “Homodyne measurement of Earth's rotation with a motion-sensing videogame controller and a record player”. 2019年9月15日閲覧。（英語）
• “Academy Pendulum Sales（Academy Pendulums）”. 2019年9月15日閲覧。
• “TV torņa pārbūves projekts”. VAS Latvijas Valsts radio un televīzijas centrs. 2019年9月15日閲覧。（ラトビア語）
• “Television tower to turn into major tourist attraction”. lsm.lv (2018年9月26日). 2019年9月15日閲覧。（英語）
• “チップ上にフーコー振子 高性能MEMSジャイロ（日経ものづくり）”. 日経BP社. 2019年9月15日閲覧。（日本語）
• “教育支援：フーコー振子（島津理科）”. 島津理科. 2019年9月15日閲覧。（日本語）

関連文献

本記事で出典として使用していない文献のうち有用なものを、発表順に示す。

論文・解説

• 鈴木将「フーコー振り子の研究」『物理教育』第29巻第3号、日本物理教育学会、1981年、202-206頁、NAID 110007489123。 
• 佐伯 純一「フーコーの振り子」『Basic数学：mathematics』第14巻第2号、現代数学社、1981年2月、35-40頁、NCID AN00000380。 
• 池田 幸夫「フーコー振子の実験と地球の自転との関係について(続・こんな教材をどう扱うか)」『地学教育と科学運動』第11巻第0号、地学団体研究会、1982年、131-134頁、NAID 110007159446。 
• 山田 盛夫「角速度のベクトル合成則とフーコー振り子振動面の回転説明モデル」『物理教育』第34巻第2号、日本物理教育学会、1986年、86-88頁、NAID 110007489529。 
• 佐々木 勝浩「実験セミナー 地学 天文その3 フーコー振り子」『SUT bulletin』第10巻第7号、東京理科大学、1993年、68-71頁。 
• 有冨 正男、富 武満「フーコー振り子の運動解析」『西部造船会々報』第87巻第0号、日本船舶海洋工学会、1994年、185-200頁、NAID 110007627546。 
• M.F. Conlin (1999). “The popular and scientific reception of the Foucault pendulum in the United States”. Isis (Isis) 90 (2): 181-204. 
• Horacio R. SALVA, et al. (2010). “A Foucault’s pendulum design”. Review of Scientific Instruments 81: 115102. 

書籍

• 杉田 公生、伊藤 達夫、山口 勝、太田 雅己『理工系のための微分方程式』培風館、1998年。 
• 朝永振一郎『物理学とは何だろうか』みすず書房〈朝永振一郎著作集〉、2001年。ISBN 4622051176。 
• William Tobin (2003). The Life and Science of Léon Foucault. Cambridge University Press. ISBN 9780521808552 
• 酒井幸市『WebGLによる 物理シミュレーション』工学社、2014年。ISBN 978-4-7775-1825-8。 
• 小畑修二『Ｃで理解を深める基礎力学』鳩山科学技術研究所、2018年。ISBN 978-4-7775-1825-8。 

外部サイト

動画

• 葛飾区郷土と天文の博物館にあるフーコーの振り子のタイムラプス撮影、約1000倍速で再生 - YouTube
• フーコーの振り子を昼間8時間連続撮影、200倍速で再生 - YouTube
• Miami University David Griggs Foucault Pendulum - YouTube（英語）
• A Full Day with The Franklin Institute's Pendulum - YouTube（英語）

解説

• 国際連合ビルのフーコーの振り子（日本語）
• ゲルフ大学物理学科のフーコーの振り子（英語）

販売

• Academy Pendulum Sales（英語）
• 教育支援：フーコー振子（島津理科）（日本語）