五角形

五角形(ごかくけい、ごかっけい、英: pentagon)は、5つの頂点と辺を持つ多角形の総称。
正五角形
[編集]正五角形は、各辺の長さが等しく、内角も108°(中心角は72°)と一定な五角形である。辺の長さを a とすると
- 面積
- 内接円の半径
- 外接円の半径
正五角形の作図
[編集]
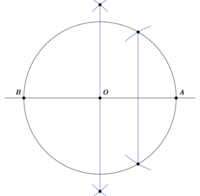
正五角形(regular pentagon)は定規とコンパスによる作図が可能である。以下に示すのは古典的な方法の一つである。
|

|

|

|
| (1) | (2) | (3) | (4) |
- 直線上の一点Oを中心にとった円を描画し、直線と交わる二点をA, Bとする。ABの垂直二等分線、およびOAの垂直二等分線を作図する。
- OAとその垂直二等分線が交わる点をC、円OとABの垂直二等分線が交わる点のうち一つをDとする。CDを半径にとり、Cを中心にDからABまで弧を描画する。弧とABが交わる点をEとする。
- DEを半径にとり、Dを中心に弧を描画する。弧が円Oと交わる二点をF, Gとする。
- 同じ半径のままF, Gを中心とした弧を描画する。これらの弧が円Oと交わる五点D, F, G, I, Hを結ぶ図形が正五角形である。
-
正方形のマス目上での正五角形の描き方
-
正五角形の領域をその高さと外接円心の高さの比を利用して求め出す方法の一例
定理
[編集]- 正五角形の一辺と対角線との比は、黄金比に等しい。
- 正五角形の交わる対角線は、互いに他を黄金比に分ける。
- 対角線の長さが互いに全て等しい正多角形は、正五角形と正四角形(正方形)のみである。
- n 角形の対角線の本数を m 本としたとき n = m が成り立つのは n = 5、すなわち五角形だけである。
種類
[編集]五等辺五角形
[編集]五等辺五角形は5つ辺が同じ長さの五角形である。しかし、五角形の5つの内角は値の0~180度の範囲を取ることができるため、複数の五角形の集まりを形成することが可能である。[要校閲]また、正五角形も5つの辺全てが等しいため五等辺五角形と言える。
-
五等辺五角形の例
-
正五角形も五等辺五角形の一つである。
-
2つの角が直角の五等辺五角形
共円五角形
[編集]
共円五角形は、外接円と呼ばれる円が、すべての5つの頂点を通過している五角形である。正五角形は、共円五角形の一つである。共円五角形の面積は、規則的であるかどうかに関係なく、係数が五角形の辺の関数である七次方程式の根の1つの平方根の4分の1として表すことができる[1][2][3]。
ロビンスの五角形
[編集]有理数の辺と有理数の面積を持つ循環五角形が存在する。これは、ロビンスの五角形と呼ばれている[4]。ロビンスの五角形の対角線はすべて有理数またはすべて無理数でなければならないことが証明されており、すべての対角線は有理数でなければならないと推測される[4]。
直角五角形
[編集]直角五角形は直角の角を持つ五角形である。五角形は1つ、2つまたは3つの直角を持つことが可能であり、通常五角形は4つや5つの直角はは持つことができない[5]。しかし、双曲幾何学においてはすべての内角が直角の五角形を描くことができる[6]。五角形の2つの直角と3つの直角には、2つの種類があり、直角は、連続する場合と連続しない場合がある[5]。正五角形には直角は無いため、直角五角形ではない[5]。
-
一つの角が直角の直角五角形
-
二つの角が直角かつ連続している直角五角形。
-
二つの角が直角かつ連続していない直角五角形。
五等角五角形
[編集]5つの角の大きさが全て等しい五角形。等角五角形の1つの角の大きさは108°になる[7][8]。
-
五等角五角形の例
-
五等角五角形の例
-
正五角形も五等角五角形の一つである。
-
五等角五角形の例
凸五角形
[編集]すべての凸五角形において、対角線の平方の合計は、辺の平方の合計の3倍未満である[9]。
凹五角形
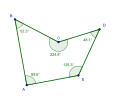
[編集]五角形の角度の少なくとも1つが180°を超える場合、凹五角形になる[10][11]。
-
凹五角形の例
-
凹五等辺五角形の例
その他五角形に関する事項
[編集]
この節に雑多な内容が羅列されています。 |
正五角形関連
[編集]- 五角形の対角線を繋いだ星形を五芒星(ペンタグラム)という。たとえば長崎市の市章などはペンタグラムとなっている。
- 細長い紙片、(またはリボンや割り箸袋など)で一重結びの結び目を作ると正五角形が得られる。
- アメリカ国防総省を俗にペンタゴンというが、これはバージニア州にある本省庁舎が五角形であることに由来する。こちらを指す時には定冠詞「The」が冠される。
- 函館市の五稜郭も外郭に突き出した三角形を組み合わせた五角形の「稜堡式(りょうほしき)」を採用した星形要塞である。これは、要塞設計と構造特性上、外敵からの攻撃に対する死角を防ぎ、稜堡の一辺が当時の銃の射程以内に収まり、どの方向から襲撃されても対応しやすいといった、守備に適した非常に合理的な形状と考えられたためである。
- シタデル (ケベック)も星形要塞である。
- 飯塚伊賀七の作った茨城県つくば市谷田部にある五角堂は、五角形をした建築物である[12]。
- ヒトデやウニなど、棘皮動物の体制は五放射相称を基本とする。
- 植物の世界では、バラ科やナス科などのように五枚の花びらで構成された五弁花が多く、数列におけるフィボナッチ数であることが知られている。

- 円石藻の一種のビゲロイは、炭酸カルシウムからなる正五角形の鱗片(コッコリス、円石)に覆われている[13]。
- で、これに黄金比をかけると 1/2 になる。つまり、2sin18° は黄金比の逆数である。
- 五角数は多角数の一つである。
- 正五角形の1つの頂点からの2本の対角線と1辺とでできる三角形は黄金三角形である。
- 水平な底辺を持つ正五角形の右下の辺の傾きは「高さ×2/底辺の長さ」となっている。
- 正五角形の内接円と外接円の半径の比は φ : 2 となっている。
-
水平な底辺を持つ正五角形の右下の辺の傾きは「高さ×2/底辺の長さ」となっている。
-
正五角形の内接円と外接円の半径の比は φ : 2となっている。
-
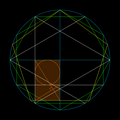
赤の正円に外接する正方形を縦横それぞれに8等分してできるマス目(青)を活用すると、図のように赤の正円に内接する正五角形(橙)とその正五角形に内接する正円(黄)を描くことができる。
-
同一の正円(青)に内接する正五角形(黄)と正六角形(緑)を活用して黄金長方形(橙)を作り出す例
-
正円(緑)の半径と同じ長さの辺を持つ正方形(青)を活用した正五角形(橙)や五芒星(黄)の描き方の例(赤の円は描き上げ後の検証のためのもの)
-
正円半径と同じ長さの辺の正方形を活用した内接正五角形(五芒星)の描き方の一例(赤の円は描き上げ後の検証のためのもの)
正五角形以外
[編集]脚注
[編集]- ^ Weisstein, Eric W.. “Cyclic Pentagon” (英語). mathworld.wolfram.com. 2021年12月12日閲覧。
- ^ Robbins, D. P. (1994-12-01). “Areas of polygons inscribed in a circle” (英語). Discrete & Computational Geometry 12 (2): 223–236. doi:10.1007/BF02574377. ISSN 1432-0444.
- ^ Robbins, David P. (1995). “Areas of Polygons Inscribed in a Circle”. The American Mathematical Monthly 102 (6): 523–530. doi:10.2307/2974766. ISSN 0002-9890.
- ^ a b Buchholz, Ralph H.; MacDougall, James A. (2008-01-01). “Cyclic polygons with rational sides and area” (英語). Journal of Number Theory 128 (1): 17–48. doi:10.1016/j.jnt.2007.05.005. ISSN 0022-314X.
- ^ a b c RobertLovesPi (2013年10月22日). “A Survey of Right Angles in Convex Pentagons” (英語). RobertLovesPi.net. 2021年12月12日閲覧。
- ^ “直角正五角形”. web1.kcn.jp. 2021年12月12日閲覧。
- ^ “hw 8 solutions.pdf”. 2021年12月15日閲覧。
- ^ hmong.wiki. “等角ポリゴン” (英語). www.asianprofile.wiki. 2021年12月15日閲覧。
- ^ “Inequalities proposed in “Crux Mathematicorum””. 2021年12月15日閲覧。
- ^ “Concave Pentagon - Geometry Calculator”. rechneronline.de. 2021年12月15日閲覧。
- ^ “Pentagon”. www.math.net. 2021年12月15日閲覧。
- ^ 「日研」新聞編集委員会 編(1991):184ページ
- ^ 萩野恭子 et al. 2011.
参考文献
[編集]- 高木貞治『数学小景』岩波書店〈岩波現代文庫〉、2002年、ISBN 4006000812。
- 「日研」新聞編集委員会 編『茨城108景をめぐる』川崎松濤監修、筑波書林、1991年9月20日、pp.219。
- 萩野恭子、堀口健雄、高野義人、松岡裕美「サイズ変化を伴った円石藻の種分化」『日本プランクトン学会報』2011年、ISSN 03878961。