「球面」の版間の差分
FlatLanguage (会話 | 投稿記録) m 仮リンク解消 |
|||
| (17人の利用者による、間の31版が非表示) | |||
| 1行目: | 1行目: | ||
{{About|三次元空間内の二次元図形|一般の球面|超球面|中身の詰まった立体図形|球体}} |
|||
{{出典の明記|date=2015年9月}} |
|||
[[ |
[[Image:Sphere wireframe 10deg 6r.svg|right|thumb|球面の二次元[[投影図]]]] |
||
[[初等幾何学]]や[[ユークリッド幾何学]]において、'''球面'''(きゅうめん、{{lang-en-short|''sphere''{{efn|{{lang-grc-short|[[wikt:σφαῖρα|σφαῖρα]]}} (''sphaira'') に由来}}}})とは、[[三次元空間]]において、与えられた[[定点]]からの距離が一定値 {{mvar|r}} をもつような[[軌跡 (数学)|点全体の成す集合]]である{{sfn|Albert|2016|p=54}}。このとき、与えられた[[定点]]をこの球面の'''[[中心]]'''といい、距離 {{mvar|r}} をこの球面の'''[[半径]]'''という。また、球面の中心を通る[[直線]]が、球面から切り取られる[[線分]]の[[長さ]]は常に一定であり、半径の二倍に等しい。これを球面の'''[[直径]]'''と呼ぶ。 |
|||
「どの方向から観察しても、半径 {{mvar|r}} の[[円 (数学)|円]]に見える[[立体図形]]」と定義することもできる。 |
|||
'''球面'''(きゅうめん)とは[[球|球体]]の[[表面]]の意である。[[数学]]における球面 {{lang|en|(sphere)}} は、距離の定められた[[空間]]の定点からの[[距離空間|距離]]が一定であるような点の軌跡として定義される、非常に高い[[対称性]]を示す[[図形]]である。球面の囲む有界領域を[[球体]]あるいは単に球 {{lang|en|(ball)}} と呼ぶ。一般には三次元[[ユークリッド空間]] ''E''<sup>3</sup> 内のもの、つまり二次元球面を指す場合が多い。 |
|||
緩い言い方や数学以外の文脈では、「[[球]]」「球面」「[[球体]]」の3つが[[同義語]]として用いられたり、"sphere" と "ball" の意味が入れ違っていたりすることもあるが、数学的には球面 (''sphere'') は三次元[[ユークリッド空間]]に[[埋め込み (数学)|埋め込まれた]]二次元[[閉曲面]]であり、球体 (''ball'') は三次元空間内の球面および球面の囲む「内側」である(いまのように球面を含める場合を特に「[[閉球体]]」と呼び、囲む領域に球面をまったく含めない場合には「[[開球体]]」と呼ぶ。)。 |
|||
== 定義 == |
|||
[[距離空間]] (''X'', ''d'') において、一点 ''c'' を固定するとき、''c'' から一定距離 ''r'' > 0 を隔てる点全体の成す集合 |
|||
この区別は必ず守られるというようなものではないし、特に古い文献では中身の詰まった図形を「球」(sphere) としている。これは[[ユークリッド平面|二次元]]の場合に、「円」が(中身の詰まった)「[[円板]]」の意味だったり(境界である)「[[円周]]」の意味だったりするのとちょうど同じである。 |
|||
{{Indent|<math>U_r(c) = U(c;r):=\{x\in X\mid d(x,c)=r\}</math>}} |
|||
== {{vanc|球面の方程式|ユークリッド球面}} == |
|||
を、''c'' を中心(ちゅうしん、{{lang|en|center}})とする[[半径]](はんけい、{{lang|en|radius}})''r'' の'''球面'''と呼ぶ。''r'' → 0 の極限で一点集合 {''c''} となるので、''r'' = 0 の場合を退化した球面として扱う場合もある。 |
|||
[[Image:Sphere and Ball.png|right|thumb|two orthogonal radii of a sphere]] |
|||
{{see also|三角函数|球面座標系}} |
|||
[[解析幾何学]]において、{{math|(''x''{{sub|0}}, ''y''{{sub|0}}, ''z''{{sub|0}})}} を中心とする半径 {{mvar|r}} の球面(ユークリッド球面)は <math display="block"> (x - x_0 )^2 + (y - y_0 )^2 + ( z - z_0 )^2 = r^2</math> を満たす点 {{math|(''x'', ''y'', ''z'')}} 全体の[[軌跡 (数学)|軌跡]]である。 |
|||
{{mvar|a, b, c, d, e}} は実数で {{math|''a'' ≠ 0}} なるものとし、<math display="block">x_0 := \frac{-b}{a}, \quad y_0 := \frac{-c}{a}, \quad z_0 := \frac{-d}{a}, \quad \rho := \frac{b^2 +c^2+d^2 - ae}{a^2}</math> と書けば、上記の方程式は <math display="block">f(x,y,z) := a(x^2 + y^2 +z^2) + 2(bx + cy + dz) + e = 0</math> の形になる。一般にこの形の方程式({{math|''x''{{exp|2}}, ''y''{{exp|2}}, ''z''{{exp|2}}}} の係数が等しく、{{mvar|xy, yz, zx}} の項を持たない三変数二次多項式方程式)が与えられたならば、以下の何れか一つのみが成り立つ:{{sfn|Albert|2016|p=54}} |
|||
== ユークリッド球面 == |
|||
* {{mvar|''ρ'' < 0}} のときは、この方程式に解となる実点は存在せず、'''虚球''' (''imaginary sphere'') の方程式と呼ぶ。 |
|||
''xyz''-[[直交座標系]]を持つ三次元ユークリッド空間において、定点 (''x''<sub>0</sub>, ''y''<sub>0</sub>, ''z''<sub>0</sub>) からの距離が ''r'' の点 (''x'', ''y'', ''z'') は式 |
|||
* {{math|1=''ρ'' = 0}} のとき、方程式 {{math|1=''f''(''x'', ''y'', ''z'') = 0}} は中心となる一点 {{math|''P''{{sub|0}} {{coloneqq}} (''x''{{sub|0}}, ''y''{{sub|0}}, ''z''{{sub|0}})}} のみを解とし、'''点球''' (''point sphere'') の方程式と言う。 |
|||
* {{math|''ρ'' > 0}} のときには、{{math|1=''f''(''x'', ''y'', ''z'') = 0}} は {{math|''P''{{sub|0}}}} を中心とする半径 {{math|''r'' {{coloneqq}} {{sqrt|''ρ''}}}} の球面の方程式となる(上のふたつと対照する場合、'''実球''' (''real sphere'') の方程式と言う)。 |
|||
上記の方程式で {{math|1=''a'' = 0}} としたならば {{math|1=''f''(''x'', ''y'', ''z'') = 0}} は平面の方程式となる。そこで平面を[[無限遠点]]を中心とする半径無限大の球と考えることができる{{sfn|Woods|1961|p=266}}。 |
|||
{{Indent|<math>(x - x_0 )^2 + (y - y_0 )^2 + ( z - z_0 )^2 = r^2</math>}} |
|||
{{math|(''x''{{sub|0}}, ''y''{{sub|0}}, ''z''{{sub|0}})}} を中心とする半径 {{mvar|r}} の球面上の点は <math display="block">\begin{cases} |
|||
を満たす。このような点すべての集合が球面である。''r'' = 1 の場合は特に'''[[単位球面]]'''という。その[[面積]]は ''S'' = 4π''r''<sup>2</sup> である。半径に依らず、原点中心の球面が持つ幾何学的な特性は微分方程式 |
|||
x = x_0 + r\sin(\varphi)\cos(\theta)\\ |
|||
y = y_0 + r\sin(\varphi)\sin(\theta)\\ |
|||
z = z_0 + r\cos(\varphi) |
|||
\end{cases}\qquad (0 \leq \varphi \leq \pi,\; 0 \leq \theta < 2\pi )</math> と媒介表示できる{{sfn|Kreyszig|1972|p=342}}。 |
|||
原点を中心とする任意の半径を持つ球面は[[微分形式]] <math display="bock"> x\mathit{dx} + y\mathit{dy} + z\mathit{dz} = 0</math> の積分曲面である。この微分形の方程式は、位置ベクトル {{math|(''x'', ''y'', ''z'')}} と速度ベクトル {{math|(''dx'', ''dy'', ''dz'')}} が全球面に亙って常に互いに[[直交]]するという事実を反映している。 |
|||
{{Indent|<math>x\,dx + y\,dy + z\,dz = (x,y,z)\begin{pmatrix}dx\\dy\\dz\end{pmatrix}= 0</math>}} |
|||
球面は、[[円周]]をその任意の[[直径]]を軸に回転させた[[回転曲面]]として構成することもできる。円周は特別な種類の[[楕円]]であるから、球面は特別な種類の[[回転楕円体|回転楕円面]]である。円を回転させる代わりに楕円をその[[長軸]]を軸に回転させると[[長球]]、[[短軸]]を軸にすれば[[扁球]]となる。{{sfn|Albert|2016|p=60}} |
|||
によって表すことができる。特に、各点 (''x'', ''y'', ''z'') においてその接ベクトル (''dx'', ''dy'', ''dz'') は球面と[[直交]]する。 |
|||
== {{vanc|囲む体積|体積}} == |
|||
一般に自然数 ''n'' に対して、実 ''n'' + 1 次元[[ユークリッド空間]]における点集合 |
|||
[[File:Esfera Arquímedes0.svg|thumb|球面とその外接円筒]] |
|||
三次元空間において、球面の囲む[[体積]](厳密に言えばこれは「[[球体]]」の体積だが、古典的にはこれを「球」の体積と呼ぶ)は、半径を {{mvar|r}} として <math display="block">V = \frac{4}{3}\pi r^3</math> で与えられる。この公式を導いた最初の人は[[アルキメデス]]で、球面の囲む体積が球面とそれに外接する[[円柱 (数学)|円筒]](つまり、円筒の高さおよび底面の直径が球面の直径と等しい)の間の体積に二倍に等しいことを示すことで導かれた{{sfn|Steinhaus|1969|p=223}}。この主張は、[[カヴァリエリの原理]]から得ることができる。この公式を積分を使って導くこともできる: 原点を中心とする半径 {{mvar|r}} の球を想定すれば、{{ill2|輪切り積分法|en|disk integration}}では、中心が {{mvar|x}}-軸に沿って {{math|1=''x'' = −''r''}} から {{math|1=''x'' = ''r''}} まで並ぶように無限個積み重ねた無限に薄い円柱 (≈ [[円板]]) の体積の総和として球面の体積を計算する。あるいは、[[球面座標系]]の体積要素 <math display="inline">dV := r^2\sin(\theta)\mathit{dr}\,\mathit{d\theta}\,\mathit{d\varphi}</math> を積分しても同じ結果が得られる。 |
|||
{{Indent|<math>S^n = {\partial B^{n+1}} = \{ (x_1, \ldots, x_n, x_{n+1}) \in R^{n+1} \mid x_1^2 + \cdots + x_n^2 + x_{n+1}^2 = r^2 \}</math>}} |
|||
== {{vanc|面積|表面積}} == |
|||
として原点を中心とする ''n''-'''次元球面''' が定義される。省略して ''n''-球面ということもある。ここでいう次元 ''n'' は[[多様体]]としての次元である。上で説明した3次元空間の単位球面は 2-球面 ''S''<sup>2</sup> にあたる。2-球面の場合と同様 ''r'' = 1 の場合を単位球面と呼ぶ。また、''n'' ≥ 3 の場合を特に'''[[超球面]]''' {{lang|en|(hypersphere)}} と呼んで通常の 2-球面と区別することがある。 |
|||
半径 {{mvar|r}} の球面の[[表面積]]は <math display="block">A := 4\pi r^2</math> で与えられる。この公式の最初の発見者[[アルキメデス]]は<ref name=MathWorld_Sphere>{{MathWorld |title=Sphere |id=Sphere}}</ref>、外接円筒の側面への射影が面積を保つという事実から公式を導いた{{sfn|Steinhaus|1969|p=221}}。 |
|||
公式を導く別なやり方は、これが同じく半径 {{mvar|r}} の球の体積の {{mvar|r}} に関する[[微分]]に等しいという事実を利用することである。これは、半径 {{mvar|r}} の球の内部の全体積を、半径 {{math|0}} から {{mvar|r}} までの無限に薄い球殻を無限個{{underline|半径に垂直に}}積み重ねた体積の総和として捉えることとして理解できる。無限に薄いという条件により、各球殻の内側と外側の表面積の差は無限小であり、半径 {{mvar|r}} に対応する球殻の体積は単に半径 {{mvar|r}} の球面の表面積と無限に小さい厚みとの積として得られることに注意する。あるいはまた、[[球面座標系]]における球面の[[面積要素]] {{math|1=''dA'' {{coloneqq}} ''r''{{sup|2}}sin(''θ'')⋅''dθ⋅dφ''}} の積分としても導出できる。 |
|||
たとえば、[[円周]]は 1 次元の球面 ''S''<sup>1</sup> であり、1-次元単位球面は[[単位円]]である。また、原点を中心とする半径 ''r'' の 0 次元球面とは、原点に関する[[対蹠点]](たいせきてん)の対 { −''r'', ''r'' } である。 |
|||
== 幾何学的性質 == |
|||
また実数全体 '''R''' を例えば複素数全体 '''C''' に置き換えても同様の定義ができ、その場合には単位球面を ''S''<sup>''n''</sup> ('''C''') などと表すこともある。 |
|||
球面は[[共面性|同一平面上]]にない四点を指定すれば一意に決定される。より一般に、通る点や平面に接するなどの条件が四つあれば球面が一意に決まる{{sfn|Albert|2016|p=55}}。この性質は、平面上の円が[[共線性|同一直線上]]にない三点で一意に決まるという性質の三次元空間版と見ることができる。その帰結として、球面は一つの円とその円が属する平面上にない一点によって(それらすべてを通るという意味で)一意に決定できる。 |
|||
ふたつの球面の方程式の共通解を調べれば、ふたつの球面の交線が円となることが確認できる。その交円を含む平面は交わる球面の'''根面''' (''radical plane'') という{{sfn|Albert|2016|p=57}}。根面は実平面だけれども、交円は虚円(二つの球面が共通実点を持たない)や点円(二つの球面が一点で[[接する]])となることもあり得る{{sfn|Woods|1961|p=267}} |
|||
一方、たとえ空間が '''R'''<sup>2</sup> であってもユークリッド距離でなく 1-[[ノルム]]から来る距離 ''d''<sub>1</sub>(''x'', ''y'') = |''x''<sub>1</sub> − ''y''<sub>1</sub>| + |''x''<sub>2</sub> − ''y''<sub>2</sub>| (''x'' = (''x''<sub>1</sub>, ''x''<sub>2</sub>), ''y'' = (''y''<sub>1</sub>, ''y''<sub>2</sub>)) を持ち出せば、これによって定義される単位球面(単位円)は |
|||
4 点 (1, 0), (0, 1), (−1, 0), (0, −1) を頂点とする四辺形 { (''x'', ''y'') ∈ '''R'''<sup>2</sup> | |''x''| + |''y''| = 1 } |
|||
であるというように、一風変わったものが球面と呼ばれることになる。 |
|||
交円上の実点における二つの球面の間の成す角とは、その点における各球面の接平面によって定義される[[二面角]]を言う。二つの球面は、その交円上のどの点でも同じ角度で交わる{{sfn|Albert|2016|p=58}}。ふたつの球面が[[直交|直角に交わる]]ための必要十分条件は、それら球面の中心間の距離の平方がそれらの半径の平方和に等しいことである{{sfn|Woods|1961|p=266}}。 |
|||
=== 大円 === |
|||
球面と[[平面]]が交わるとき、共通部分は[[円_(数学)|円]]となる。このうち交差する平面が球の中心を通る場合にできる円の半径は最も大きくなり、特に'''大円'''(だいえん、great circle)と呼ばれる<ref>地球の大円は[[大圏]]と呼ばれる。</ref>。これは[[測地線]]となっている。 |
|||
=== 球束 === |
|||
[[地球]]を近似的に球と見れば、[[赤道]]や[[経線]](子午線)、[[卯酉線]]などが大円の例である。対して、赤道以外の[[緯線]]は大円ではない。 |
|||
{{seealso|直線束 (射影幾何学)|円束 (射影幾何学)}} |
|||
相異なる二つの球面の方程式 {{math|1=''f''(''x'', ''y'', ''z'') = 0}} および {{math|1=''g''(''x'', ''y'', ''z'') = 0}} に対して <math display="block">s f(x,y,z) + t g(x,y,z) = 0</math> は、助変数 {{mvar|s, t}} の任意の値に対して、やはり球面の方程式を与える。適当な {{mvar|t, s}} に対してこの方程式を満足する球面すべてからなる[[族 (数学)|族]]を、もとのふたつの球面(生成球面)から定まる'''球[[束 (射影幾何学)|束]]'''または'''球面束''' (''pencil of spheres'') と呼ぶ。ただし、この定義において「球面」には平面(無限遠点中心、半径無限大)の場合も許すものとする。生成球面が両方とも平面である場合には、球面束を成すすべての球面が平面となるか、さもなくば球面束はただ一つの平面(生成球面の根面)のみからなる{{sfn|Woods|1961|p=266}}。 |
|||
球面束がすべて平面からなるのでないならば、それを以下の三種に分類することができる{{sfn|Woods|1961|p=267}}: |
|||
== 球面のトポロジー == |
|||
* 生成球面の交円が実円 {{mvar|C}} ならば、球面束は {{mvar|C}} を含む球面(根面も含めて)全体の成す族になる。球面束に属する通常の球面(平面でないという意味)の中心の軌跡(中心直線)は {{mvar|C}} の中心を通り根面に直交する直線上にある。 |
|||
[[位相幾何学]]では、必ずしも距離を持たない位相空間 ''X'' がユークリッド幾何学的な球面と[[同相]]であるとき、''X'' を球面と呼ぶ。この意味での球面は境界の無い向きがついたコンパクト[[多様体#位相多様体|位相多様体]]の一例である。この場合必ずしも微分構造を区別しないが、微分構造を区別するとき、ユークリッド球面に同相であるが異なる微分構造を持つ位相空間を[[異種球面]](エキゾチック球面)と呼ぶ。また、ホモトピーやホモロジーでは球面と区別の付かない位相空間をそれぞれ[[ホモトピー球面]]や[[ホモロジー球面]]などと呼ぶ。これらの位相空間の間に成り立つ重要な関係を記述するものの一つに[[ポアンカレ予想]]が知られている。 |
|||
* 生成球面の交円が虚円ならば、球面束に属する球面はこの虚円を通るが、通所の球面としてはそれらは交わらない(共通実点はない)。属する球面の中心直線は根面(これは虚円を含む平面で球面束に属す)に直交する。 |
|||
* 生成球面の交円が点円 {{mvar|A}} ならば、束に属する球面は全て点 {{mvar|A}} において接し、根面は束に属するすべての球面の共通接平面である。中心直線は {{mvar|A}} において根面と直交する。 |
|||
根面上の固定された点から束に属する任意の球面に引いた接線の長さは、球面に依らず同じになる{{sfn|Woods|1961|p=267}}。 |
|||
例えば、0 次元球面は相異なる二点、1 次元球面は[[円周]]である。 |
|||
根面は、束に属する球面すべてに直交する任意の球面の中心が描く軌跡に等しい。もっと言えば、球面束に属する球面の任意のふたつに直交する球面は、束に属するすべての球面と直交し、かつ中心が束の根面上にある{{sfn|Woods|1961|p=267}}。 |
|||
実数直線 '''R''' に一点{∞}を付け加えた空間は、[[位相幾何学]]的には円周である。 |
|||
== 用語法 == |
|||
{{Indent|これは次のようにするとよくわかる。'''R''' を ''x'' 軸とする ''xy''- 平面を考え、そこに原点と点 (0, 1) を結ぶ線分を直径とする円を描く。さらに、点 (0, 1) を通る直線族 ''y'' = ''mx'' + 1 (''m'' ≠ 0) を考えると、個々の直線は点 (0, 1) を除く円周上の各点と ''x'' 軸とにそれぞれただ一点のみで交わるので、円と ''x'' 軸上の点とを一対一に対応させることができる。そこで点 (0, 1) に対応する仮想的な[[無限遠点]] {∞} を付け加えた集合(に自然な位相を入れた位相空間)と円周とは[[同相]]になる。}} |
|||
球の中心を通る直線上にある球面上の点の対(その直線と球面とのふたつの交点)は{{ill2|対蹠点 (数学)|en|antipodal point|label=対蹠点}} (antipodal points) と呼ばれる。球と中心および半径を共有する球面上の円は[[大円]]と言い、大円により球面は二つの合同な図形に分けられる。球面の{{ill2|平面切断|en|plane section}}は「球面切断」(球面断面)という。球面切断はすべて円であり、そのうちで大円でないものは{{ill2|球面上の円|en|Circle of a sphere|label=小円}}と呼ばれる<ref>{{MathWorld |id=SphericSection |title=Spheric section}}</ref>。 |
|||
二つの相異なる非対蹠点の間の球面に沿った最短距離とは、それら二点を結ぶただ一つの大円がその二点で切り取られる二つの弧のうちの小さいほう(精確には大きくないほう)の長さである。この「[[大円距離]]」を備えた球面上で大円は{{ill2|リーマン円|en|Riemannian circle}}となる。 |
|||
同様に、n 次元[[ユークリッド空間]]'''R'''<sup>n</sup> に唯一つの[[無限遠点]] {∞} を付け加えた(つまり[[一点コンパクト化]]した)位相空間は'''S'''<sup>n</sup>と同相である。 |
|||
球面上の特定の点を任意に選んで「北極」とするとき、その対蹠点を「南極」と呼んで、両極点から等距離にある大円を[[赤道]]とする。二つの極点を結ぶ大円は[[子午線]]または[[経線]]と呼び、球の内部を通って両極を結ぶ直線を[[自転軸]]と呼ぶ。赤道と平行となる球面上の円は[[緯線]]である。このような語法は、近似的に[[楕円体]]である([[地球]]のような)[[惑星]]に対しても用いられるものである([[ジオイド]]も参照)。 |
|||
[[射影幾何学|射影直線]] '''RP(1)''' は '''S'''<sup>1</sup> と同相である。ただし、これを次元に関して一般化させることはできず、例えば[[射影平面]] '''RP(2)''' は '''S'''<sup>2</sup> と同相でない。 |
|||
== {{vanc|半球面|半球}} == |
|||
球面の中心を含む任意の平面は、球面をふたつの合同な'''半球面''' (''hemisphere'') に分割する。球面の中心を通り交わる任意のふたつの平面は、四つの{{ill2|球面楔形|en|spherical lune}}または球面二角形に細分割する(これら図形の頂点は、平面の交線上にある{{ill2|対蹠点 (数学)|label=対蹠点|en|antipodal point}}に一致する)。 |
|||
球面の対蹠点を同一視する[[商集合|商]]は{{ill2|実射影平面|en|real projective plane}}と呼ばれる曲面で、これを赤道にある対蹠点を同一視した[[北半球]]と見ることもできる。 |
|||
{{訳語疑問点範囲|この半球面は{{ill2|リーマン円|en|Riemannian circle}}によって最適(面積最小)等長充填となると{{ill2|充填面積予想|en|filling area conjecture|label=予想}}されている。|date=2018年11月}} |
|||
== 一般化 == |
|||
=== {{vanc|任意次元|超球面}} === |
|||
{{Main|超球面|超球の体積}} |
|||
球面の概念を、任意の[[次元 (数学)|次元]]に対して一般化することができる。[[自然数]] {{mvar|n}} に対して「{{mvar|n}}-次元(ユークリッド)球面」("{{mvar|n}}-sphere") をしばしば {{mvar|S{{sup|n}}}} と書いて、中心となる定点から半径となる決まった距離 {{mvar|r}} の位置にある ({{math|''n'' + 1}})-次元ユークリッド空間内の点からなる軌跡として定義できる。特に |
|||
* 零次元球面 {{math|''S''<sup>0</sup>}} は[[実数直線]]内の閉区間 {{math|[−''r'', ''r'']}} の両端点である。 |
|||
* 一次元球面 {{math|''S''<sup>1</sup>}} は半径 {{mvar|r}} の[[円周]]である。 |
|||
* 二次元球面 {{math|''S''<sup>2</sup>}} は通常の球面 |
|||
* [[三次元球面]] {{math|''S''<sup>3</sup>}} は四次元ユークリッド空間内の超球面を表す |
|||
{{math|''n'' > 2}} のとき、[[超球面]]ともいう{{efn|[[超立方体]]などと同じく「高次元」図形で相当するものという意味で「超」球面と呼んでいる}}。文献によっては{{ill2|余次元|en|codimension}}が 1 のときに限って[[超球面 (超曲面)|超球面]]と呼ぶ{{efn|この「超-」の使い方は、[[超平面]]などと同じ語法である。}}場合も稀にあるので文脈に注意すべきである。 |
|||
{{mvar|S{{sup|n}}}} は、特に「単位球面」(原点を中心とする単位半径の球面)を表すために用いられることもある。 |
|||
({{math|''n'' − 1}})-次元単位超球面の表面積は、[[ガンマ函数]] {{math|Γ(''z'')}} を用いて <math display="block">\frac{2 \pi^{n/2}}{\Gamma(n/2)}</math> で与えられる。 |
|||
=== {{vanc|距離空間|距離球面}} === |
|||
より一般に、[[距離空間]] {{math|(''E'', ''d'')}} において、中心 {{mvar|x}} および半径 {{math|''r'' > 0}} の球面(距離球面)は {{math|1=''d''(''x'',''y'') = ''r''}} なる点 {{mvar|y}} の軌跡として定義される。 |
|||
中心が {{mvar|E}} の「原点」として捉えられる識別点にとるとき(例えば、[[ノルム空間]]は原点を持つ距離空間である)、定義や記法にその点は現れないかもしれない。半径を {{math|1}} に取るとき、[[単位球面]]と呼ぶのは従来通りである。 |
|||
距離[[球体]]の場合と異なり、距離球体はそれが十分大きい半径を持つ場合でも空集合となり得る。例えば{{math|'''Z'''<sup>''n''</sup>}} に[[ユークリッド距離]]を入れるとき、半径 {{mvar|r}} の球面は空でないのは {{math|''r''<sup>2</sup>}} が {{mvar|n}} 個の整数の平方和に書けるときに限る。 |
|||
=== 位相球面 === |
|||
[[位相幾何学]]では、{{math|''n'' + 1}} 次元(位相)球体の境界に[[同相]]な空間として {{mvar|n}}-次元(位相)球面は定義される。これは {{mvar|n}}-次元ユークリッド球面([[#超球面|通常の]] {{mvar|n}}-次元球面)に[[同相]]となるが、必ずしも[[距離空間|距離付けられ]]ない。 |
|||
* 零次元位相球面は、[[離散位相]]の入った点の対である。 |
|||
* 一次元位相球面は、[[同相]]の[[違いを除いて]]円周である。たとえば、任意の[[結び目 (数学)|結び目]]は一次元位相球面となる。 |
|||
* 二次元位相球面は、同相の違いを除いて通常の球面である。例えば、任意の[[楕円体]]は二次元位相球面となる。 |
|||
{{mvar|n}}-次元位相球面もまた {{mvar|S{{sup|n}}}} と書かれる。位相球面は[[境界付き位相多様体|境界]]のない[[コンパクト空間|コンパクト]][[位相多様体]]の例になっている。必ずしも[[可微分多様体]](滑らかな多様体)ではないが、滑らかな場合であってもユークリッド球面に[[微分同相]]とは限らない。 |
|||
[[ハイネ–ボレルの被覆定理]]により {{mvar|n}}-次元ユークリッド球面がコンパクトであることが分かる。実際、球面は連続函数 {{math|{{norm|''x''}}}} による一点集合の逆像であるから閉集合であり、また {{mvar|S{{sup|n}}}} は有界である。 |
|||
驚嘆すべきことに、三次元空間内において自己交叉することを許せば、通常の球面を一切の切れ目を入れることなく裏返すことができる。この一連の方法は {{ill2|球の裏返し|en|sphere eversion}} (sphere eversion) と呼ばれる。 |
|||
== 球面幾何学 == |
|||
[[Image:Sphere halve.png|thumb|right|球面上の[[大円]]]] |
|||
{{Main|球面幾何学}} |
|||
ユークリッドの[[平面幾何学]]の基本要素は[[点 (数学)|点]]と[[直線]]である。球面上でも、点は通常の意味で定義できる。「直線」に相当するものは[[測地線]]で、いまの場合具体的には[[大円]]である。大円を定義づける特徴は、その上にある点すべてを含む平面が球の中心を通ることである。[[弧長]]によって距離を測ることにすれば、球面上の任意の二点を結ぶ最短経路が、それらの点を含む大円がそれら点で切り取られる円弧のうちの短いほうによって与えられることが証明できる。 |
|||
[[古典幾何学]]における多くの定理が球面幾何学においても真となるが、球面上では古典幾何の[[公準]]がすべて満足されるわけではない([[平行線公準]]などは成立しない)から、真とはならない定理も存在する。[[球面三角法]]において、[[角度|角]]は大円の間で定義される。球面三角法は通常の[[三角法]]とは様々な点で異なる。例えば、[[球面三角形]]の内角の和は常に {{math|180°}} より大きい。あるいはまた、任意の互いに{{ill2|相似三角形|en|similar triangles|label=相似}}なふたつの球面三角形は[[図形の合同|合同]]である。 |
|||
== 球面に関する11の性質 == |
|||
[[Image:Sphere section.png|thumb|球面の法ベクトル、法平面およびその法断面。交線の曲率は断面曲率である。球面に対して与えられた点を通る各法断面は同じ半径(それは球の半径に等しい)を持つ円になる。これは球面上の任意の点が臍点であることを意味する。]] |
|||
[[ダフィット・ヒルベルト]]と{{ill2|シュテファン・コーン゠フォッセン|en|Stephan Cohn-Vossen}}の著書 ''Geometry and the Imagination''<ref>{{cite book |
|||
|last1=Hilbert |first1= David |author1-link= David Hilbert |last2= Cohn-Vossen |first2= Stephan |
|||
|title=Geometry and the Imagination |
|||
|edition=2nd |
|||
|year=1952 |
|||
|publisher=Chelsea |
|||
|isbn=0-8284-1087-9}}</ref>で彼らは、球面の11の性質を記述し、それらの性質が球面を一意に決定するかどうかについて論じた。それらのうちのいくつかは(半径無限大の球面と看做せる)[[平面]]も満足する。それら11性質とは: |
|||
# 「球面上のすべての点は一つの定点から同一の距離にある。また、ふたつの定点からそれら点への距離の比は一定である」 |
|||
#: [注釈] 前半は球面の通常の定義で、球面を一意に決定する。後半は容易に導かれ、[[円周]]に対する[[ペルガのアポロニウス]]の[[アポロニウスの円|結果]]と同様のことが従う。後半の内容は平面も満たす。 |
|||
# 「球面の等高線および平面切断はすべて円である」 |
|||
#: [注釈] この性質は球面を一意に定義する。 |
|||
# 「球面は幅が一定かつ周長が一定である」 |
|||
#: [注釈] 曲面の幅は平行な接平面の対の間の距離として測る。他にもいくつか定幅の凸閉曲面はあり、たとえば{{ill2|マイスナーの立体|en|Meissner body}}はそうである。曲面の周長 (girth) は、曲面を平面上に直交射影した像の境界の外周の長さである。これらの性質の各々は他の性質を導く。 |
|||
# 「球面上のすべてのてんは{{ill2|臍点|en|umbilic}}である」 |
|||
#: [注釈] 球面の法線は球の中心から放射状に延びる直線であるから、曲面上の任意の点において[[法線|法方向]]は曲面に直角である。法線を含む平面との交線は「法断面」と呼ばれる曲線をなし、その曲線の曲率を「法曲率」と呼ぶ。多くの曲面に対してその上の点の多くは異なる切断に対して異なる曲率を持つ。それら曲率の中で最大および最小の値を持つものを[[主曲率]]と言う。任意の閉曲面は少なくとも四つの「臍点」と呼ばれる点を持つ。臍点にいてすべての断面曲率(特にふたつの主曲率)は等しい。臍点は曲面を球面で極めて近似できる点と見なすことができる。 |
|||
#: 球面に対しては全ての法断面の曲率が等しいから、任意の点が臍点である。この性質を満たす曲面は、球面と平面に限る。 |
|||
# 「球面は中心曲面を持たない」 |
|||
#: [注釈] 与えられた法断面に対して、断面曲率に等しい曲率を持ち曲面に接する円が存在して、その中心線は法線上に載る。例えば、最大および最小断面曲率に対応する中心点は「焦点」と呼ばれ、そのような中心点全体の成す集合は{{ill2|焦面|en|focal surface}}を成す。 |
|||
#: 大半の曲面では焦面は二葉曲面(それぞれが曲面となるような二つの集合)を成し、ふたつの葉は臍点で交わる。いくつかの場合は特別である: |
|||
#:* {{ill2|管状曲面|en|channel surface}}の場合、一葉は曲線でありもう一葉は曲面となる。 |
|||
#:* [[円錐]]、円筒、[[トーラス]]、{{ill2|デュパンのサイクライド|en|Dupin cyclide|label=サイクライド}}の場合は、二葉とも曲線を成す。 |
|||
#:* 球面の場合、任意の接触円の中心は球の中心であり、焦面は一点となる。この性質は球面に対して一意である。 |
|||
# 「球面の任意の測地線は閉曲線である」 |
|||
#: [注釈] [[測地線]]は曲面上の曲線で、二点間の最短距離を与えるものである。これは平面上の直線の概念を一般化するものである。球面上の測地線は大円。この性質を満足する曲面は他にもたくさんある。 |
|||
# 「与えられた体積を持つすべての立体の中で、球は表面積が最も小さくなるもののひとつである。与えられた表面積を持つすべての立体の中で、球は最も大きい体積を持つものの一つである」 |
|||
#: [注釈] これは[[等周定理|等周不等式]]から従う。これらの性質は球面を一意に定義し、その定義の仕方は[[シャボン玉]]のようなものと思える—シャボン玉は決まった体積を囲んで、その体積に対して表面積は[[表面張力]]が極小(最小)化されるように決まる。だから自由に浮かぶシャボン玉は球面を近似する(重力のような外力がシャボン玉の形状をやや歪ませる)。 |
|||
# 「与えられた表面積を持つすべての凸立体のなかで、球面は最も小さい全平均曲率を持つ」 |
|||
#: [注釈] {{ill2|平均曲率|en|Mean curvature}}は二つの主曲率の平均で、球面は全ての点で二つの主曲率が一定であるから、平均曲率も一定。 |
|||
# 「球面は一定の平均曲率を持つ」 |
|||
#: [注釈] 球面は境界も特異点もなく正の一定平均曲率を持つ唯一の埋め込まれた曲面である。他に一定の平均曲率を持つ埋め込まれた曲面に[[極小曲面]]がある。 |
|||
# 「球面は正の一定ガウス曲率を持つ」 |
|||
#: [注釈] [[ガウス曲率]]は二つの主曲率の積である。ガウス曲率は、曲面上の長さや角度を測ることで決定され、その曲面の空間への埋め込みの仕方に依らないという意味で、曲面の持つ内在的な性質である。したがって、曲面を曲げてもガウス曲率は変わらず、またほかの正の一定ガウス曲率を持つ曲面は球面に小さな切れ目を入れてそれを曲げることで得ることができる。そうして得られた球面以外の曲線は[[境界を持つ多様体|境界を持ち]]、球面は境界を持たない正の一定ガウス曲率を持つ唯一の曲面となる。[[擬球面]]は負の一定ガウス曲率を持つ曲面の例である。 |
|||
# 「剛体運動の三径数族によって球面は球面自身に変形される」 |
|||
#: [注釈] 原点を中心とする単位球面について、任意の座標軸回りの回転でこの球面は自身に写る。原点を通る任意の直線周りの回転は、三座標軸周りの回転の組み合わせで表すことができる([[オイラー角]]の項を参照)から、先の球面をそれ自身に写す任意の回転からなる回転の三径数族が存在する(この族は三次元[[回転群]] {{math|''SO''(3)}} である)。ほかに変換の三径数族を持つ曲面は、平面(この場合の族は、{{mvar|x}}-軸および {{mvar|y}}-軸に沿った[[平行移動]]と原点を中心とする回転で径数付けられる)に限る。円筒は剛体運動のに径数族を持つ唯一の曲面であり、一径数族を持つ曲面は[[回転曲面]]および{{ill2|螺旋面|en|helicoid}}に限る。 |
|||
== ギャラリー == |
|||
<gallery mode="packed" heights="200px" style="text-align:left"> |
|||
Image:Einstein gyro gravity probe b.jpg|An image of one of the most accurate human-made spheres, as it [[refraction|refracts]] the image of [[Albert Einstein|Einstein]] in the background. This sphere was a [[fused quartz]] [[gyroscope]] for the [[Gravity Probe B]] experiment, and differs in shape from a perfect sphere by no more than 40 atoms (less than 10 [[nanometers]]) of thickness. It was announced on 1 July 2008 that [[オーストラリア|Australia]]n scientists had created even more nearly perfect spheres, accurate to 0.3 nanometers, as part of an international hunt to find a new global standard [[kilogram]].<ref>[https://www.newscientist.com/article/dn14229-roundest-objects-in-the-world-created.html New Scientist | Technology | Roundest objects in the world created]</ref> |
|||
File:King of spades- spheres.jpg|Deck of playing cards illustrating engineering instruments, England, 1702. [[King of spades]]: Spheres |
|||
</gallery> |
|||
== 関連項目 == |
== 関連項目 == |
||
{{div col||colwidth=20em}} |
|||
{{Commons|Sphere}} |
|||
* [[球]] |
* [[三次元球面]] |
||
* {{ill2|アフィン球面|en|Affine sphere}} |
|||
* [[円 (数学)|円]] |
|||
* [[アレクサンダーの角付き球面]] |
|||
* [[単位円]] |
|||
* [[ |
* [[天球]] |
||
* [[ |
* [[立方体]] |
||
* [[ |
* [[曲率]] |
||
* [[方向統計学]] |
|||
* [[ダイソン球]] |
|||
* {{ill2|写像球体を持つ手|en|Hand with Reflecting Sphere}}: [[マウリッツ・エッシャー]]による、表面が鏡である球面の光学的性質と鏡像を形にした自画像 |
|||
* [[ホバーマンスフィア]] |
|||
* {{ill2|ホモロジー球面|en|Homology sphere}} |
|||
* {{ill2|球面のホモトピー群|en|Homotopy groups of spheres}} |
|||
* {{ill2|ホモトピー球面|en|Homotopy sphere}} |
|||
* [[超球面 (余次元1)]] |
|||
* {{ill2|レーナルト球|en|Lenart Sphere}} |
|||
* [[ナプキンリング問題]] |
|||
* [[オーブ]] |
|||
* [[擬球面]] |
|||
* [[リーマン球面]] |
|||
* [[立体角]] |
|||
* [[球充填]] |
|||
* [[球冠]] |
|||
* [[球面座標系]] |
|||
* [[地球球体説]] |
|||
* [[球面螺旋]]: 定歳差を持つ曲線の{{ill2|接線標形|en|tangent indicatrix}} |
|||
* {{ill2|球面扇形|en|Spherical sector}} |
|||
* [[球台]] |
|||
* {{ill2|球殻|en|Spherical shell}} |
|||
* {{ill2|球面楔形|en|Spherical wedge}}(蹄状体) |
|||
* [[球帯]] |
|||
* {{ill2|ゾル曲面|en|Zoll surface|label=ゾル球面}} |
|||
{{div col end}} |
|||
== |
== 注 == |
||
{{脚注ヘルプ}} |
|||
<references/> |
|||
=== 注釈 === |
|||
{{notelist}} |
|||
=== 出典 === |
|||
{{reflist|30em}} |
|||
== 参考文献 == |
|||
*{{citation|first=Abraham Adrian|last=Albert|title=Solid Analytic Geometry|year=2016|origyear=1949|publisher=Dover|isbn=978-0-486-81026-3}} |
|||
*{{cite book|first=William |last=Dunham |pages=28, 226 |title=The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems and Personalities |isbn=0-471-17661-3 }} |
|||
* {{ citation | first1 = Erwin | last1 = Kreyszig | year = 1972 | isbn = 0-471-50728-8 | title = Advanced Engineering Mathematics | edition = 3rd | publisher = [[John Wiley & Sons|Wiley]] | location = New York }} |
|||
*{{citation|first=H.|last=Steinhaus|title=Mathematical Snapshots|year=1969|publisher=Oxford University Press|edition=Third American}} |
|||
*{{citation|first=Frederick S.|last=Woods|title=Higher Geometry / An Introduction to Advanced Methods in Analytic Geometry|year=1961|origyear=1922|publisher=Dover}} |
|||
== 外部リンク == |
|||
{{Wikisource1911Enc|Sphere}} |
|||
* {{MathWorld |id=Sphere |title=Sphere}} |
|||
* [http://mathschallenge.net/index.php?section=faq&ref=geometry/surface_sphere Surface area of sphere proof.] |
|||
* {{nlab|urlname=sphere|title=sphere}} |
|||
* {{PlanetMath|urlname=spheremetricspace|title=sphere (metric space)}} |
|||
* {{ProofWiki|urlname=Definition:Sphere|title=Definition:Sphere}} |
|||
* {{SpringerEOM|urlname=Sphere|title=Sphere|first=I.S. |last=Sharadze}} |
|||
{{Normdaten}} |
{{Normdaten}} |
||
{{デフォルトソート:きゆうめん}} |
|||
{{DEFAULTSORT:きゆうめん}} |
|||
[[Category:球面|*]] |
|||
[[Category:閉曲面]] |
[[Category:閉曲面]] |
||
[[Category:初等数学]] |
[[Category:初等数学]] |
||
[[Category:等質空間]] |
[[Category:等質空間]] |
||
[[Category:数学に関する記事]] |
[[Category:数学に関する記事]] |
||
[[Category:立体図形]] |
|||
[[Category:回転体]] |
|||
2024年10月15日 (火) 02:26時点における最新版

初等幾何学やユークリッド幾何学において、球面(きゅうめん、英: sphere[注釈 1])とは、三次元空間において、与えられた定点からの距離が一定値 r をもつような点全体の成す集合である[1]。このとき、与えられた定点をこの球面の中心といい、距離 r をこの球面の半径という。また、球面の中心を通る直線が、球面から切り取られる線分の長さは常に一定であり、半径の二倍に等しい。これを球面の直径と呼ぶ。
「どの方向から観察しても、半径 r の円に見える立体図形」と定義することもできる。
緩い言い方や数学以外の文脈では、「球」「球面」「球体」の3つが同義語として用いられたり、"sphere" と "ball" の意味が入れ違っていたりすることもあるが、数学的には球面 (sphere) は三次元ユークリッド空間に埋め込まれた二次元閉曲面であり、球体 (ball) は三次元空間内の球面および球面の囲む「内側」である(いまのように球面を含める場合を特に「閉球体」と呼び、囲む領域に球面をまったく含めない場合には「開球体」と呼ぶ。)。
この区別は必ず守られるというようなものではないし、特に古い文献では中身の詰まった図形を「球」(sphere) としている。これは二次元の場合に、「円」が(中身の詰まった)「円板」の意味だったり(境界である)「円周」の意味だったりするのとちょうど同じである。
球面の方程式
[編集]
解析幾何学において、(x0, y0, z0) を中心とする半径 r の球面(ユークリッド球面)は を満たす点 (x, y, z) 全体の軌跡である。
a, b, c, d, e は実数で a ≠ 0 なるものとし、 と書けば、上記の方程式は の形になる。一般にこの形の方程式(x2, y2, z2 の係数が等しく、xy, yz, zx の項を持たない三変数二次多項式方程式)が与えられたならば、以下の何れか一つのみが成り立つ:[1]
- ρ < 0 のときは、この方程式に解となる実点は存在せず、虚球 (imaginary sphere) の方程式と呼ぶ。
- ρ = 0 のとき、方程式 f(x, y, z) = 0 は中心となる一点 P0 ≔ (x0, y0, z0) のみを解とし、点球 (point sphere) の方程式と言う。
- ρ > 0 のときには、f(x, y, z) = 0 は P0 を中心とする半径 r ≔ √ρ の球面の方程式となる(上のふたつと対照する場合、実球 (real sphere) の方程式と言う)。
上記の方程式で a = 0 としたならば f(x, y, z) = 0 は平面の方程式となる。そこで平面を無限遠点を中心とする半径無限大の球と考えることができる[2]。
(x0, y0, z0) を中心とする半径 r の球面上の点は と媒介表示できる[3]。
原点を中心とする任意の半径を持つ球面は微分形式 の積分曲面である。この微分形の方程式は、位置ベクトル (x, y, z) と速度ベクトル (dx, dy, dz) が全球面に亙って常に互いに直交するという事実を反映している。
球面は、円周をその任意の直径を軸に回転させた回転曲面として構成することもできる。円周は特別な種類の楕円であるから、球面は特別な種類の回転楕円面である。円を回転させる代わりに楕円をその長軸を軸に回転させると長球、短軸を軸にすれば扁球となる。[4]
囲む体積
[編集]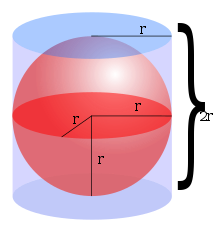
三次元空間において、球面の囲む体積(厳密に言えばこれは「球体」の体積だが、古典的にはこれを「球」の体積と呼ぶ)は、半径を r として で与えられる。この公式を導いた最初の人はアルキメデスで、球面の囲む体積が球面とそれに外接する円筒(つまり、円筒の高さおよび底面の直径が球面の直径と等しい)の間の体積に二倍に等しいことを示すことで導かれた[5]。この主張は、カヴァリエリの原理から得ることができる。この公式を積分を使って導くこともできる: 原点を中心とする半径 r の球を想定すれば、輪切り積分法では、中心が x-軸に沿って x = −r から x = r まで並ぶように無限個積み重ねた無限に薄い円柱 (≈ 円板) の体積の総和として球面の体積を計算する。あるいは、球面座標系の体積要素 を積分しても同じ結果が得られる。
面積
[編集]半径 r の球面の表面積は で与えられる。この公式の最初の発見者アルキメデスは[6]、外接円筒の側面への射影が面積を保つという事実から公式を導いた[7]。
公式を導く別なやり方は、これが同じく半径 r の球の体積の r に関する微分に等しいという事実を利用することである。これは、半径 r の球の内部の全体積を、半径 0 から r までの無限に薄い球殻を無限個半径に垂直に積み重ねた体積の総和として捉えることとして理解できる。無限に薄いという条件により、各球殻の内側と外側の表面積の差は無限小であり、半径 r に対応する球殻の体積は単に半径 r の球面の表面積と無限に小さい厚みとの積として得られることに注意する。あるいはまた、球面座標系における球面の面積要素 dA ≔ r2sin(θ)⋅dθ⋅dφ の積分としても導出できる。
幾何学的性質
[編集]球面は同一平面上にない四点を指定すれば一意に決定される。より一般に、通る点や平面に接するなどの条件が四つあれば球面が一意に決まる[8]。この性質は、平面上の円が同一直線上にない三点で一意に決まるという性質の三次元空間版と見ることができる。その帰結として、球面は一つの円とその円が属する平面上にない一点によって(それらすべてを通るという意味で)一意に決定できる。
ふたつの球面の方程式の共通解を調べれば、ふたつの球面の交線が円となることが確認できる。その交円を含む平面は交わる球面の根面 (radical plane) という[9]。根面は実平面だけれども、交円は虚円(二つの球面が共通実点を持たない)や点円(二つの球面が一点で接する)となることもあり得る[10]
交円上の実点における二つの球面の間の成す角とは、その点における各球面の接平面によって定義される二面角を言う。二つの球面は、その交円上のどの点でも同じ角度で交わる[11]。ふたつの球面が直角に交わるための必要十分条件は、それら球面の中心間の距離の平方がそれらの半径の平方和に等しいことである[2]。
球束
[編集]相異なる二つの球面の方程式 f(x, y, z) = 0 および g(x, y, z) = 0 に対して は、助変数 s, t の任意の値に対して、やはり球面の方程式を与える。適当な t, s に対してこの方程式を満足する球面すべてからなる族を、もとのふたつの球面(生成球面)から定まる球束または球面束 (pencil of spheres) と呼ぶ。ただし、この定義において「球面」には平面(無限遠点中心、半径無限大)の場合も許すものとする。生成球面が両方とも平面である場合には、球面束を成すすべての球面が平面となるか、さもなくば球面束はただ一つの平面(生成球面の根面)のみからなる[2]。
球面束がすべて平面からなるのでないならば、それを以下の三種に分類することができる[10]:
- 生成球面の交円が実円 C ならば、球面束は C を含む球面(根面も含めて)全体の成す族になる。球面束に属する通常の球面(平面でないという意味)の中心の軌跡(中心直線)は C の中心を通り根面に直交する直線上にある。
- 生成球面の交円が虚円ならば、球面束に属する球面はこの虚円を通るが、通所の球面としてはそれらは交わらない(共通実点はない)。属する球面の中心直線は根面(これは虚円を含む平面で球面束に属す)に直交する。
- 生成球面の交円が点円 A ならば、束に属する球面は全て点 A において接し、根面は束に属するすべての球面の共通接平面である。中心直線は A において根面と直交する。
根面上の固定された点から束に属する任意の球面に引いた接線の長さは、球面に依らず同じになる[10]。
根面は、束に属する球面すべてに直交する任意の球面の中心が描く軌跡に等しい。もっと言えば、球面束に属する球面の任意のふたつに直交する球面は、束に属するすべての球面と直交し、かつ中心が束の根面上にある[10]。
用語法
[編集]球の中心を通る直線上にある球面上の点の対(その直線と球面とのふたつの交点)は対蹠点 (antipodal points) と呼ばれる。球と中心および半径を共有する球面上の円は大円と言い、大円により球面は二つの合同な図形に分けられる。球面の平面切断は「球面切断」(球面断面)という。球面切断はすべて円であり、そのうちで大円でないものは小円と呼ばれる[12]。
二つの相異なる非対蹠点の間の球面に沿った最短距離とは、それら二点を結ぶただ一つの大円がその二点で切り取られる二つの弧のうちの小さいほう(精確には大きくないほう)の長さである。この「大円距離」を備えた球面上で大円はリーマン円となる。
球面上の特定の点を任意に選んで「北極」とするとき、その対蹠点を「南極」と呼んで、両極点から等距離にある大円を赤道とする。二つの極点を結ぶ大円は子午線または経線と呼び、球の内部を通って両極を結ぶ直線を自転軸と呼ぶ。赤道と平行となる球面上の円は緯線である。このような語法は、近似的に楕円体である(地球のような)惑星に対しても用いられるものである(ジオイドも参照)。
半球面
[編集]球面の中心を含む任意の平面は、球面をふたつの合同な半球面 (hemisphere) に分割する。球面の中心を通り交わる任意のふたつの平面は、四つの球面楔形または球面二角形に細分割する(これら図形の頂点は、平面の交線上にある対蹠点に一致する)。
球面の対蹠点を同一視する商は実射影平面と呼ばれる曲面で、これを赤道にある対蹠点を同一視した北半球と見ることもできる。
この半球面はリーマン円によって最適(面積最小)等長充填となると予想されている。[訳語疑問点]
一般化
[編集]任意次元
[編集]球面の概念を、任意の次元に対して一般化することができる。自然数 n に対して「n-次元(ユークリッド)球面」("n-sphere") をしばしば Sn と書いて、中心となる定点から半径となる決まった距離 r の位置にある (n + 1)-次元ユークリッド空間内の点からなる軌跡として定義できる。特に
- 零次元球面 S0 は実数直線内の閉区間 [−r, r] の両端点である。
- 一次元球面 S1 は半径 r の円周である。
- 二次元球面 S2 は通常の球面
- 三次元球面 S3 は四次元ユークリッド空間内の超球面を表す
n > 2 のとき、超球面ともいう[注釈 2]。文献によっては余次元が 1 のときに限って超球面と呼ぶ[注釈 3]場合も稀にあるので文脈に注意すべきである。
Sn は、特に「単位球面」(原点を中心とする単位半径の球面)を表すために用いられることもある。
(n − 1)-次元単位超球面の表面積は、ガンマ函数 Γ(z) を用いて で与えられる。
距離空間
[編集]より一般に、距離空間 (E, d) において、中心 x および半径 r > 0 の球面(距離球面)は d(x,y) = r なる点 y の軌跡として定義される。
中心が E の「原点」として捉えられる識別点にとるとき(例えば、ノルム空間は原点を持つ距離空間である)、定義や記法にその点は現れないかもしれない。半径を 1 に取るとき、単位球面と呼ぶのは従来通りである。
距離球体の場合と異なり、距離球体はそれが十分大きい半径を持つ場合でも空集合となり得る。例えばZn にユークリッド距離を入れるとき、半径 r の球面は空でないのは r2 が n 個の整数の平方和に書けるときに限る。
位相球面
[編集]位相幾何学では、n + 1 次元(位相)球体の境界に同相な空間として n-次元(位相)球面は定義される。これは n-次元ユークリッド球面(通常の n-次元球面)に同相となるが、必ずしも距離付けられない。
- 零次元位相球面は、離散位相の入った点の対である。
- 一次元位相球面は、同相の違いを除いて円周である。たとえば、任意の結び目は一次元位相球面となる。
- 二次元位相球面は、同相の違いを除いて通常の球面である。例えば、任意の楕円体は二次元位相球面となる。
n-次元位相球面もまた Sn と書かれる。位相球面は境界のないコンパクト位相多様体の例になっている。必ずしも可微分多様体(滑らかな多様体)ではないが、滑らかな場合であってもユークリッド球面に微分同相とは限らない。
ハイネ–ボレルの被覆定理により n-次元ユークリッド球面がコンパクトであることが分かる。実際、球面は連続函数 ‖ x ‖ による一点集合の逆像であるから閉集合であり、また Sn は有界である。
驚嘆すべきことに、三次元空間内において自己交叉することを許せば、通常の球面を一切の切れ目を入れることなく裏返すことができる。この一連の方法は 球の裏返し (sphere eversion) と呼ばれる。
球面幾何学
[編集]
ユークリッドの平面幾何学の基本要素は点と直線である。球面上でも、点は通常の意味で定義できる。「直線」に相当するものは測地線で、いまの場合具体的には大円である。大円を定義づける特徴は、その上にある点すべてを含む平面が球の中心を通ることである。弧長によって距離を測ることにすれば、球面上の任意の二点を結ぶ最短経路が、それらの点を含む大円がそれら点で切り取られる円弧のうちの短いほうによって与えられることが証明できる。
古典幾何学における多くの定理が球面幾何学においても真となるが、球面上では古典幾何の公準がすべて満足されるわけではない(平行線公準などは成立しない)から、真とはならない定理も存在する。球面三角法において、角は大円の間で定義される。球面三角法は通常の三角法とは様々な点で異なる。例えば、球面三角形の内角の和は常に 180° より大きい。あるいはまた、任意の互いに相似なふたつの球面三角形は合同である。
球面に関する11の性質
[編集]
ダフィット・ヒルベルトとシュテファン・コーン゠フォッセンの著書 Geometry and the Imagination[13]で彼らは、球面の11の性質を記述し、それらの性質が球面を一意に決定するかどうかについて論じた。それらのうちのいくつかは(半径無限大の球面と看做せる)平面も満足する。それら11性質とは:
- 「球面上のすべての点は一つの定点から同一の距離にある。また、ふたつの定点からそれら点への距離の比は一定である」
- [注釈] 前半は球面の通常の定義で、球面を一意に決定する。後半は容易に導かれ、円周に対するペルガのアポロニウスの結果と同様のことが従う。後半の内容は平面も満たす。
- 「球面の等高線および平面切断はすべて円である」
- [注釈] この性質は球面を一意に定義する。
- 「球面は幅が一定かつ周長が一定である」
- [注釈] 曲面の幅は平行な接平面の対の間の距離として測る。他にもいくつか定幅の凸閉曲面はあり、たとえばマイスナーの立体はそうである。曲面の周長 (girth) は、曲面を平面上に直交射影した像の境界の外周の長さである。これらの性質の各々は他の性質を導く。
- 「球面上のすべてのてんは臍点である」
- [注釈] 球面の法線は球の中心から放射状に延びる直線であるから、曲面上の任意の点において法方向は曲面に直角である。法線を含む平面との交線は「法断面」と呼ばれる曲線をなし、その曲線の曲率を「法曲率」と呼ぶ。多くの曲面に対してその上の点の多くは異なる切断に対して異なる曲率を持つ。それら曲率の中で最大および最小の値を持つものを主曲率と言う。任意の閉曲面は少なくとも四つの「臍点」と呼ばれる点を持つ。臍点にいてすべての断面曲率(特にふたつの主曲率)は等しい。臍点は曲面を球面で極めて近似できる点と見なすことができる。
- 球面に対しては全ての法断面の曲率が等しいから、任意の点が臍点である。この性質を満たす曲面は、球面と平面に限る。
- 「球面は中心曲面を持たない」
- 「球面の任意の測地線は閉曲線である」
- [注釈] 測地線は曲面上の曲線で、二点間の最短距離を与えるものである。これは平面上の直線の概念を一般化するものである。球面上の測地線は大円。この性質を満足する曲面は他にもたくさんある。
- 「与えられた体積を持つすべての立体の中で、球は表面積が最も小さくなるもののひとつである。与えられた表面積を持つすべての立体の中で、球は最も大きい体積を持つものの一つである」
- 「与えられた表面積を持つすべての凸立体のなかで、球面は最も小さい全平均曲率を持つ」
- [注釈] 平均曲率は二つの主曲率の平均で、球面は全ての点で二つの主曲率が一定であるから、平均曲率も一定。
- 「球面は一定の平均曲率を持つ」
- [注釈] 球面は境界も特異点もなく正の一定平均曲率を持つ唯一の埋め込まれた曲面である。他に一定の平均曲率を持つ埋め込まれた曲面に極小曲面がある。
- 「球面は正の一定ガウス曲率を持つ」
- 「剛体運動の三径数族によって球面は球面自身に変形される」
ギャラリー
[編集]-
An image of one of the most accurate human-made spheres, as it refracts the image of Einstein in the background. This sphere was a fused quartz gyroscope for the Gravity Probe B experiment, and differs in shape from a perfect sphere by no more than 40 atoms (less than 10 nanometers) of thickness. It was announced on 1 July 2008 that Australian scientists had created even more nearly perfect spheres, accurate to 0.3 nanometers, as part of an international hunt to find a new global standard kilogram.[14]
-
Deck of playing cards illustrating engineering instruments, England, 1702. King of spades: Spheres
関連項目
[編集]注
[編集]注釈
[編集]出典
[編集]- ^ a b Albert 2016, p. 54.
- ^ a b c Woods 1961, p. 266.
- ^ Kreyszig 1972, p. 342.
- ^ Albert 2016, p. 60.
- ^ Steinhaus 1969, p. 223.
- ^ Weisstein, Eric W. "Sphere". mathworld.wolfram.com (英語).
- ^ Steinhaus 1969, p. 221.
- ^ Albert 2016, p. 55.
- ^ Albert 2016, p. 57.
- ^ a b c d Woods 1961, p. 267.
- ^ Albert 2016, p. 58.
- ^ Weisstein, Eric W. "Spheric section". mathworld.wolfram.com (英語).
- ^ Hilbert, David; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (2nd ed.). Chelsea. ISBN 0-8284-1087-9
- ^ New Scientist | Technology | Roundest objects in the world created
参考文献
[編集]- Albert, Abraham Adrian (2016) [1949], Solid Analytic Geometry, Dover, ISBN 978-0-486-81026-3
- Dunham, William. The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems and Personalities. pp. 28, 226. ISBN 0-471-17661-3
- Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley, ISBN 0-471-50728-8
- Steinhaus, H. (1969), Mathematical Snapshots (Third American ed.), Oxford University Press
- Woods, Frederick S. (1961) [1922], Higher Geometry / An Introduction to Advanced Methods in Analytic Geometry, Dover
外部リンク
[編集]- Weisstein, Eric W. "Sphere". mathworld.wolfram.com (英語).
- Surface area of sphere proof.
- sphere in nLab
- sphere (metric space) - PlanetMath.
- Definition:Sphere at ProofWiki
- Sharadze, I.S. (2001), “Sphere”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4











![An image of one of the most accurate human-made spheres, as it refracts the image of Einstein in the background. This sphere was a fused quartz gyroscope for the Gravity Probe B experiment, and differs in shape from a perfect sphere by no more than 40 atoms (less than 10 nanometers) of thickness. It was announced on 1 July 2008 that Australian scientists had created even more nearly perfect spheres, accurate to 0.3 nanometers, as part of an international hunt to find a new global standard kilogram.[14]](http://upload.wikimedia.org/wikipedia/commons/thumb/9/9b/Einstein_gyro_gravity_probe_b.jpg/447px-Einstein_gyro_gravity_probe_b.jpg)
