平面曲線の例: 双曲線 初等幾何学 における平面曲線 (へいめんきょくせん、英 : plane curve, planar curve )は、その像がひとつの平面 (特にユークリッド平面、アフィン平面 (英語版 ) 射影平面 など)に全く含まれるような曲線 を言う。例えばユークリッド平面曲線は連続写像
α
:
I
→
R
2
{\displaystyle \alpha \colon I\to \mathbb {R} ^{2}}
I は実数直線 R 区間 である。
特に、2 より大きい次元のユークリッド空間 に含まれる曲線が平面的 (planar) であるとは、曲線の定義空間に全く含まれる適当な平面が存在して、その曲線の像がその平面に全く含まれるときに言う。平面的でない空間曲線は非平面曲線 (英語版 )
平面曲線が単純 とは、それが自己交叉を持たないこと、すなわち
∀
(
t
1
,
t
2
)
∈
I
2
,
t
1
≠
t
2
⟺
α
(
t
1
)
≠
α
(
t
2
)
{\displaystyle \forall (t_{1},t_{2})\in I^{2},t_{1}\neq t_{2}\iff \alpha (t_{1})\neq \alpha (t_{2})}
もっともよく調べられる平面曲線は、微分幾何学 において調べられる可微分な場合(滑らかな曲線、区分的に滑らかな曲線)や代数幾何学 において調べられる曲線の陰伏方程式が多項式で与えられる場合(代数曲線 )である。代数曲線は18世紀以降広汎に研究されてきた。
平面曲線を表す方法の一つは、各 x に対応する y の値を与える方程式
y
=
f
(
x
)
{\displaystyle y=f(x)}
xy -平面上の点 (x , y ) がその平面曲線上の点を表すように方程式を与えることである。この種の曲線は、実函数のグラフ として曲線のグラフを与えることでも記述できる。実際、この表現法はひとつの独立変数 に関する写像
α
(
t
)
=
(
t
,
f
(
t
)
)
{\displaystyle \alpha (t)=(t,f(t))}
平面曲線はまた二変数の函数を用いて
F
(
x
,
y
)
=
0
{\displaystyle F(x,y)=0}
もっとも紛れがないという意味では、媒介変数 t ∈ I
α
:
{
x
=
ϕ
(
t
)
y
=
ψ
(
t
)
,
(
α
(
t
)
:=
(
ϕ
(
t
)
,
ψ
(
t
)
)
)
{\displaystyle \alpha \colon {\begin{cases}x=\phi (t)\\y=\psi (t)\end{cases}},\qquad (\alpha (t):=(\phi (t),\psi (t)))}
滑らかな平面曲線、すなわち望ましい正則性条件を満足する一次元のひものような対象としての曲線(「局所的に直線 に見える」平面曲線)を表し研究するためには、連続性条件は十分ではない。追加の条件として平面曲線は I 上微分可能 (フランス語版 )
α
(
t
)
=
(
ϕ
(
t
)
,
ψ
(
t
)
)
{\textstyle \alpha (t)=(\phi (t),\psi (t))}
φ, ψ がともに任意の t において微分可能であることを言う。滑らかな平面曲線は平面に含まれる一次元の滑らかな多様体 であり、この意味で各点の近傍において滑らかな函数 によって直線に写される。
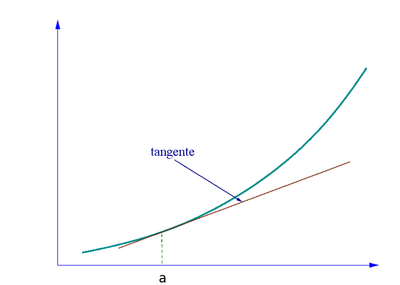
媒介表示された平面曲線が点 t 0 正則 もしくは正常 (regular) である、または点 t 0 α′ (t 0 ) ≔ (φ′ (t 0 ), ψ′ (t 0 )) ≠ (0,0)I 上で正常とは I 上の任意の t において α′ (t ) ≠ (0,0)
α′ (t 0 ) = (0,0)t 0
平面曲線上の一点における接線 曲線の正則性は、その接線 α (t )P 0 ≔ α (t 0 )P 0
α
′
(
t
0
)
=
(
ϕ
′
(
t
0
)
,
ψ
′
(
t
0
)
)
{\displaystyle \alpha '(t_{0})=(\phi '(t_{0}),\psi '(t_{0}))}
t 0 (X , Y ) は方程式
ψ
′
(
t
0
)
⋅
(
X
−
ϕ
(
t
0
)
)
−
ϕ
′
(
t
0
)
⋅
(
Y
−
ψ
(
t
0
)
)
=
0
{\displaystyle \psi '(t_{0})\cdot (X-\phi (t_{0}))-\phi '(t_{0})\cdot (Y-\psi (t_{0}))=0}
t を用いれば (X , Y ) ≔ (Xt , Yt ) は
{
X
t
=
ϕ
′
(
t
0
)
(
t
−
t
0
)
+
ϕ
(
t
0
)
Y
t
=
ψ
′
(
t
0
)
(
t
−
t
0
)
+
ψ
(
t
0
)
{\displaystyle {\begin{cases}X_{t}=\phi '(t_{0})(t-t_{0})+\phi (t_{0})\\[3pt]Y_{t}=\psi '(t_{0})(t-t_{0})+\psi (t_{0})\end{cases}}}
y = f (x )(x 0 , y 0 ) における接線は
f
′
(
x
0
)
⋅
(
x
−
x
0
)
−
(
y
−
y
0
)
=
0
{\displaystyle f'(x_{0})\cdot (x-x_{0})-(y-y_{0})=0}
F (x , y ) = 0
F
x
0
⋅
(
x
−
x
0
)
+
F
y
0
⋅
(
y
−
y
0
)
=
0
{\displaystyle F_{x_{0}}\cdot (x-x_{0})+F_{y_{0}}\cdot (y-y_{0})=0}
F x 0 F y 0 F の x, y による偏微分をそれぞれ x 0 , y 0
曲線の正則性は、その曲線の点 t 0 法線
ϕ
′
(
t
0
)
⋅
(
ϕ
(
t
0
)
−
ϕ
(
t
)
)
+
ψ
′
(
t
0
)
⋅
(
ψ
(
t
0
)
−
ψ
(
t
)
)
=
0
{\displaystyle \phi '(t_{0})\cdot (\phi (t_{0})-\phi (t))+\psi '(t_{0})\cdot (\psi (t_{0})-\psi (t))=0}
陽表示:
f
′
(
x
0
)
⋅
(
y
−
y
0
)
+
(
x
−
x
0
)
=
0
{\textstyle f'(x_{0})\cdot (y-y_{0})+(x-x_{0})=0}
陰表示:
F
y
0
⋅
(
x
−
x
0
)
+
F
x
0
⋅
(
y
−
y
0
)
=
0
{\textstyle F_{y_{0}}\cdot (x-x_{0})+F_{x_{0}}\cdot (y-y_{0})=0}
の陽にも書ける。
微分 の定義により、
ψ
′
(
t
)
ϕ
′
(
t
)
=
tan
θ
{\displaystyle {\frac {\psi '(t)}{\phi '(t)}}=\tan \theta }
傾き を表しており、右辺において正弦が引数にとる角 θ は接線が x -軸の正の半直線となす角である。この関係式を
{
cos
θ
=
±
ϕ
′
(
t
)
ϕ
′
(
t
)
2
+
ψ
′
(
t
)
2
sin
θ
=
±
ψ
′
(
t
)
ϕ
′
(
t
)
2
+
ψ
′
(
t
)
2
{\displaystyle {\begin{cases}\cos \theta =\pm {\frac {\phi '(t)}{\sqrt {\phi '(t)^{2}+\psi '(t)^{2}}}}\\[3pt]\sin \theta =\pm {\frac {\psi '(t)}{\sqrt {\phi '(t)^{2}+\psi '(t)^{2}}}}\end{cases}}}
cos(θ ) が得られる。
I 上の可微分曲線 α (t ) = (φ (t ), ψ (t ))[a , b ] ⊂ I α (a )α (b )
L
(
α
)
:=
∫
a
b
‖
α
′
(
t
)
‖
d
t
=
∫
a
b
ϕ
′
(
t
)
2
+
ψ
′
(
t
)
2
d
t
{\displaystyle L(\alpha ):=\int _{a}^{b}\|\alpha '(t)\|{\mathit {dt}}=\int _{a}^{b}{\sqrt {\phi '(t)^{2}+\psi '(t)^{2}}}\;{\mathit {dt}}}
弧長は媒介変数の取り換えに関して不変である。すなわち、β (s ) ≔ α (t (s )) (t : J → I ; s ↦ t ≔ t (s ))
L
(
α
)
=
∫
a
b
‖
α
′
(
t
)
‖
d
t
=
∫
a
b
‖
β
′
(
s
)
‖
d
s
=
L
(
β
)
{\displaystyle L(\alpha )=\int _{a}^{b}\|\alpha '(t)\|{\mathit {dt}}=\int _{a}^{b}\|\beta '(s)\|{\mathit {ds}}=L(\beta )}
[ 注釈 1]
曲線が y = f (x )x′ = 1df /dx = dy /dx
L
=
∫
a
b
1
+
(
d
y
d
x
)
2
d
x
{\displaystyle L=\int _{a}^{b}{\sqrt {1+{\Bigl (}{\frac {dy}{dx}}{\Big )}^{2}}}\;{\mathit {dx}}}
媒介変数の取り方として数学および幾何学的研究および応用において重要と考えられるものの一つに、平面極座標 が挙げられる。曲線の極座標表示が r ≔ r (θ ) (c ≤ θ ≤ d )θ に関する媒介変数表示は
{
ϕ
(
θ
)
:=
r
(
θ
)
cos
θ
ψ
(
θ
)
:=
r
(
θ
)
sin
θ
{\displaystyle {\begin{cases}\phi (\theta ):=r(\theta )\cos \theta \\\psi (\theta ):=r(\theta )\sin \theta \end{cases}}}
{
ϕ
′
(
θ
)
=
r
′
(
θ
)
cos
θ
−
r
(
θ
)
sin
θ
ψ
′
(
θ
)
=
r
′
(
θ
)
sin
θ
+
r
(
θ
)
cos
θ
{\displaystyle {\begin{cases}\phi '(\theta )=r'(\theta )\cos \theta -r(\theta )\sin \theta \\\psi '(\theta )=r'(\theta )\sin \theta +r(\theta )\cos \theta \end{cases}}}
L
=
∫
c
d
ϕ
′
(
θ
)
2
+
ψ
′
(
θ
)
2
d
θ
=
∫
c
d
r
(
θ
)
2
+
r
′
(
θ
)
2
d
θ
=
∫
c
d
r
(
θ
)
2
+
(
d
y
d
x
)
2
d
θ
{\displaystyle L=\int _{c}^{d}{\sqrt {\phi '(\theta )^{2}+\psi '(\theta )^{2}}}\;{\mathit {d\theta }}=\int _{c}^{d}{\sqrt {r(\theta )^{2}+r'(\theta )^{2}}}\;{\mathit {d\theta }}=\int _{c}^{d}{\sqrt {r(\theta )^{2}+{\Bigl (}{\frac {dy}{dx}}{\Big )}^{2}}}\;{\mathit {d\theta }}}
曲線上の座標系 または弧長変数 (弧長パラメータ)s とは、特別な種類の媒介変数表示で、積分の下の限界 a を固定し上の限界 t を変数と見るとき、積分
s
(
t
)
=
∫
a
t
‖
α
′
(
u
)
‖
d
u
{\textstyle s(t)=\int _{a}^{t}\|\alpha '(u)\|{\mathit {du}}}
t のみに依存して決まるものを言う。この積分函数 s は幾何学的には、固定された点 a から測った(必要ならば符号付き で考えた)弧長である。これにより常に曲線上にはこの曲線座標系に基づく座標を入れることが可能となる(弧長変数による媒介表示)。実際、
s
′
(
t
)
=
‖
α
′
(
t
)
‖
>
0
{\textstyle s'(t)=\|\alpha '(t)\|>0}
s (t )t ≔ t (s )
β
(
s
)
=
α
(
t
(
s
)
)
{\textstyle \beta (s)=\alpha (t(s))}
‖
β
′
(
s
)
‖
=
|
d
t
d
s
|
⋅
‖
α
′
(
t
)
‖
=
1
|
s
′
(
t
)
|
‖
α
′
(
t
)
‖
=
‖
α
′
(
t
)
‖
‖
α
′
(
t
)
‖
=
1
{\displaystyle \|\beta '(s)\|=|{\frac {dt}{ds}}|\cdot \|\alpha '(t)\|={\frac {1}{|s'(t)|}}\|\alpha '(t)\|={\frac {\|\alpha '(t)\|}{\|\alpha '(t)\|}}=1}
弧長変数で媒介表示された曲線 β (s )β′ (s )k : I → R ; s ↦ k (s ) ≔ ‖ β″ (s ) ‖ ≥ 0曲率 と呼ばれる。曲線が陽表示 y = f (x )
k
=
f
″
(
x
)
(
1
+
f
′
2
)
3
/
2
{\displaystyle k={\frac {f''(x)}{(1+f'^{2})^{3/2}}}}
F (x , y ) = 0
k
=
F
y
2
⋅
F
x
x
−
2
F
x
⋅
F
y
⋅
F
x
y
+
F
x
2
⋅
F
y
y
(
F
x
2
+
F
y
2
)
3
/
2
{\displaystyle k={\frac {F_{y}^{2}\cdot F_{xx}-2F_{x}\cdot F_{y}\cdot F_{xy}+F_{x}^{2}\cdot F_{yy}}{\left(F_{x}^{2}+F_{y}^{2}\right)^{3/2}}}}
空間内の(十分正則な)曲線はその任意の点において、フレネ標構 と呼ばれる「接ベクトル」「法ベクトル」「陪法ベクトル」の三つ組からなる参照系を持つが、このような曲線が平面的 となるための必要十分条件はその陪法ベクトルが常に零となることである。
弧長表示 β (s ) = (φ (s ), ψ (s )
T
(
s
)
=
β
′
(
s
)
=
(
ϕ
′
(
s
)
,
ψ
′
(
s
)
)
{\textstyle T(s)=\beta '(s)=(\phi '(s),\psi '(s))}
N
(
s
)
=
i
⋅
T
(
s
)
=
(
−
ψ
′
(
s
)
,
ϕ
′
(
s
)
)
{\textstyle N(s)=i\cdot T(s)=(-\psi '(s),\phi '(s))}
i は虚数単位 )。曲率を用いれば単位法ベクトルを
N
(
s
)
=
T
′
(
s
)
‖
T
′
(
s
)
‖
=
T
′
(
s
)
k
(
s
)
{\displaystyle N(s)={\frac {T'(s)}{\|T'(s)\|}}={\frac {T'(s)}{k(s)}}}
T′ は T に直交し、N に平行である。
これらをまとめると「平面曲線に関するフレネの公式 」および曲率は、任意の媒介表示曲線 α (t )
T
(
t
)
=
α
′
(
t
)
‖
α
′
(
t
)
‖
,
N
(
t
)
=
i
⋅
α
′
(
t
)
‖
α
′
(
t
)
‖
;
k
(
t
)
=
α
″
(
t
)
⋅
(
i
α
′
(
t
)
)
‖
α
′
(
t
)
‖
3
{\displaystyle {\begin{aligned}T(t)&={\frac {\alpha '(t)}{\|\alpha '(t)\|}},\quad N(t)={\frac {i\cdot \alpha '(t)}{\|\alpha '(t)\|}};\\[5pt]k(t)&={\frac {\alpha ''(t)\cdot (i\alpha '(t))}{\|\alpha '(t)\|^{3}}}\end{aligned}}}
平面代数曲線 は、アフィン平面 内の曲線で多項式方程式 f (x , y ) = 0射影平面 内の曲線で斉次多項式 方程式 F (x , y , z ) = 0
任意の平面代数曲線は、その定義多項式の次数 をその曲線の次数として持つ。代数閉体上で考える場合には、曲線の次数はそれが一般の位置 (英語版 ) x 2 + y 2 = 12 である。
次数 2 の非特異平面代数曲線は円錐曲線 であり、それらの射影完備化 は全て円 x 2 + y 2 = 1x 2 + y 2 - z 2 = 0同型 である。次数 3 の平面代数曲線は平面三次曲線 といい、それが非特異ならば楕円曲線 となる。次数 4 の平面代数曲線は平面四次曲線 (英語版 )
^ 媒介変数の取り換えに関して
β
′
(
s
)
=
d
t
d
s
(
d
ϕ
d
t
,
d
ψ
d
t
)
=
d
t
d
s
α
′
(
t
(
s
)
)
{\textstyle \beta '(s)={\frac {dt}{ds}}({\frac {d\phi }{dt}},{\frac {d\psi }{dt}})={\frac {dt}{ds}}\alpha '(t(s))}
Coolidge, J. L. (April 28, 2004), A Treatise on Algebraic Plane Curves , Dover Publications, ISBN 0-486-49576-0 Yates, R. C. (1952), A handbook on curves and their properties , J.W. Edwards, ASIN B0007EKXV0 










![{\displaystyle {\begin{cases}X_{t}=\phi '(t_{0})(t-t_{0})+\phi (t_{0})\\[3pt]Y_{t}=\psi '(t_{0})(t-t_{0})+\psi (t_{0})\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e9d1d6b41c03bca963786790225056288dd9c39)






![{\displaystyle {\begin{cases}\cos \theta =\pm {\frac {\phi '(t)}{\sqrt {\phi '(t)^{2}+\psi '(t)^{2}}}}\\[3pt]\sin \theta =\pm {\frac {\psi '(t)}{\sqrt {\phi '(t)^{2}+\psi '(t)^{2}}}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2979aa26afefcd4ac636862cd0200ac9a0b8e29)















![{\displaystyle {\begin{aligned}T(t)&={\frac {\alpha '(t)}{\|\alpha '(t)\|}},\quad N(t)={\frac {i\cdot \alpha '(t)}{\|\alpha '(t)\|}};\\[5pt]k(t)&={\frac {\alpha ''(t)\cdot (i\alpha '(t))}{\|\alpha '(t)\|^{3}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2a55a5f1b6b35c53efeb26d41e4a94014af6007)
