利用者:訳由美子/翻訳中6

量子力学は、非常に小さいものについての学問である。これは物質の振る舞いとそのエネルギーとの相互作用を原子および亜原子のスケールで説明する。古典力学は対照的に月などの天体の振る舞い含む人間の経験になじみのあるスケールでのみ物質とエネルギーを説明する。古典物理学は今でも現代的な科学技術の多くで使用されている。しかし、19世紀の終わりに向かうころ、科学者は大きい（マクロな）世界と小さい（ミクロ）世界の両方で古典物理学では説明できない現象を発見した^[1]。観察された現象と古典理論との間の矛盾を解決したいという望みは、物理学に2つの大きな革命をもたらし、元の科学的パラダイムにシフトをもたらした。相対性理論と量子力学である^[2]。この記事では物理学者が古典物理学の限界を発見し、20世紀初めの数十年で量子論の主要な概念をどのように開発したかについて説明する。これらの概念を、最初に発見されたおおよその順序で説明する。より完全な歴史については量子力学の歴史(en:History of quantum mechanics)参照。

光は粒子のような側面と波動のような側面で振る舞う。電子や原子などの粒子からなる宇宙の「もの」である物質も波動のような振る舞いを示す。ネオンライトなどの一部の光源は特定の周波数の光のみを放出する。これはネオンの原子構造により決定される明確で純粋な色が集まったものである。量子力学は、光が電磁放射の他の全ての形態とともに、光子（フォトン）と呼ばれる離散的な単位で届くことを示し、そのスペクトルエネルギー（純粋な色に対応）とその光ビームの強度を予測する。単一の光子は、電磁場の量子または観測可能な最小の粒子である。部分的な光子が実験的に観測されることはない。より広義には量子力学は、位置、速度、角運動量など古典力学におけるズームアウトな視点からは連続的に見える物体の多くの性質が（量子力学の非常に小さくズームインしたスケールで）量子化されていることを示す。素粒子のこのような性質は、小さな離散的許容値の集合のうち1つをとる必要があり、これらの値の間のギャップも小さいため、不連続性は非常に小さな（原子）スケールでのみはっきりと見ることができる。

量子力学の多くの側面は直感に反しており^[3]、大きなスケールで見られるものとはまったく異なる振る舞いを説明するため、逆説的に見えることがある。量子物理学者のリチャード・ファインマンの言葉によると、量子力学は"nature as She is—absurd"を扱っている^[4]。

例えば、量子力学の不確定性原理は、1つの測定値（粒子の位置など）をピンで止めるほど、同じ粒子に関連する別の相補的な測定値（速度など）の精度が低下することを意味する。

別の例はエンタングルメントであり、エンタングルメントでは非常に離れた2つの「エンタングルした」（もつれた）粒子の任意の2値状態（上または下に偏光された光など）のどちらかで行われる測定により、もう1つの粒子での後続の測定は常に2値のうちもう1つの値となる（反対方向に分極されるなど）。

最後の例は超流動である。超流動では温度が絶対零度近くまで冷却された液体ヘリウムの容器が、重力に逆らって容器の開口部を超えて（ゆっくりと）自発的に上昇する。

最初の量子理論: マックス・プランクと黒体放射

→詳細は「紫外破綻」を参照

熱放射は物体の内部エネルギーによって物体の表面から放出される電磁放射である。物体が十分に加熱されると物体は赤熱し、スペクトルの赤端で発光を開始する。

さらに過熱すると、色が赤から黄、白、青に変化し、より短い波長（より高い周波数）の光を発するようになる。完全な放射体は完全な吸収体でもある。冷たいとき、そのような物体は当たる全ての光を吸収し何も放出しないため完全に黒く見える。したがって理想的な熱放射体は黒体と呼ばれ、それが放出する放射は黒体放射と呼ばれる。

物体から放出されるさまざまな周波数の熱放射量の予測。プランクの法則（緑）により予測される正しい値は、レイリー・ジーンズの法則（赤）及びヴィーン近似（青）の古典的な値とは対照的である。

19世紀後半、熱放射は実験的にかなりよく特徴づけられていた^{[note 1]}。しかし、古典物理学では、レイリー・ジーンズの法則が導かれた。これは図に示すように低周波数では実験結果とよく一致するが、高周波数では全く一致しない。物理学者は全ての実験結果を説明する1つの理論を探した。

熱放射の全スペクトルを説明することができた最初のモデルは、1900年にマックス・プランクにより提案された^[5]。彼は熱放射が調和振動子の集合と平衡状態にある数学的なモデルを提案した。実験結果を再現するために、各振動子が任意の量のエネルギーを放出できるのではなく、単一の特徴的な周波数で整数単位のエネルギーを放出すると仮定する必要があった。言い換えると、振動子から放出されるエネルギーは「量子化」された^{[note 2]}。プランクによると、各振動子のエネルギーの量子は振動子の周波数に比例する。このときの比例定数は今日プランク定数として知られている。プランク定数は通常 $h$ と書かれ、値は 6.63×10⁻³⁴ J s である。そのため、周波数 $f$ の振動子のエネルギー $E$ は次式で与えられる。

E=nhf,\quad {\text{where}}\quad n=1,2,3,\ldots

^[6]

そのような放射体の色を変えるには、その温度を変える必要がある。プランクの法則はその理由を説明している。物体の温度を上げると、全体として多くのエネルギーを放出できるようになり、エネルギーの大部分がスペクトルの紫端に向かうことを意味する。

プランクの法則は物理学における最初の量子論であり、プランクは「エネルギー量子の発見による物理学の進展への貢献」により1918年にノーベル賞を受賞した^[7]。しかし、当時のプランクの見解は量子化は（現在考えられているように）世界の理解における根本からの変化ではなく、純粋にヒューリスティックな数学的構成であるというものであった^[8]。

光子: 光の量子化

1905年、アルベルト・アインシュタインはさらに一歩進めた。彼は量子化は単なる数学的構成ではなく光線のエネルギーが実際には個々のパケット（今日、光子（フォトン）と呼ばれる）で生じることを提案した^[9]。周波数 $f$ の光の単一光子のエネルギーは周波数にプランク定数 $h$ （非常に小さな正の数）を掛けたもので与えられる。

E=hf

何世紀にもわたり、科学者たちは光の2つのとりうる理論の間で議論してきた。波であるか、それとも小さな粒子の流れで構成されているか？　19世紀までに、屈折、回折、干渉、偏光などの観測された効果を説明することができたため、議論は波動の理論を支持して解決されたと一般的には考えられていた^[10]。ジェームズ・クラーク・マクスウェルは、電気、磁気、光が全て同じ現象、電磁場の現れであることを示した。古典電磁気学の法則の一式であるマクスウェル方程式は光を波として記述する。つまり、振動する電場と磁場の組み合わせである。波動理論を支持する証拠が優勢であったため、アインシュタインのアイデアは最初は非常に懐疑的に受け取られた。しかし、最終的には光子モデルが支持されるようになった。これを支持する最も重要な証拠の1つは光電効果のいくつかの不可解な特性を説明できたことであり、次節で説明する。それにも関わらず、波動のアナロジーは、光の他の特性、つまり回折、屈折、干渉を理解するのに不可欠なままであった。

光電効果

→詳細は「光電効果」を参照

1887年、ハインリヒ・ヘルツは、十分の周波数の光が金属表面にあたると、その表面が電子を放出することを観測した^[11]。1902年、フィリップ・レーナルトは、放出される電子の可能な最大エネルギーが光の強度ではなく周波数に関連していており、周波数が低すぎると、強度に関係なく電子は放出されないことを発見した。スペクトルの赤端の方の強い光線は電位をまったく生じさせない可能性があるが、スペクトルの紫端の方の弱い光線はより高い電圧を生じさせうる。電子を放出させる可能性のある光の最低周波数はしきい値周波数と呼ばれ、金属により異なる。この観測結果は、電子のエネルギーが入射する放射の強度に比例するはずであると予測する古典電磁気学と矛盾する^[12]^:24。よって、物理学者たちは最初に光電効果を示す装置を発見したとき、当初はより高い強度の光では光電装置からより高い電圧が生成されると予想していた。

アインシュタインは光線が粒子の流れ（光子）であり、その光の周波数が $f$ の場合、各光子のエネルギーは $hf$ に等しいと仮定してこの効果を説明した^[11]。電子は単一の光子によってのみ打たれる可能性が高く、最大で $hf$ のエネルギーを電子に与える^[11]。したがって、光線の強度は効果がなく^{[note 3]}、その周波数のみが電子に与えうる最大エネルギーを決定する^[11]。

しきい値効果を説明するために、アインシュタインは金属から電子を取り除くには、仕事関数と呼ばれ、 $φ$ と書かれる一定量のエネルギーが必要であると主張した^[11]。このエネルギー量は金属ごとに異なる。光子のエネルギーが仕事関数よりも小さい場合、金属から電子を取り除くのに十分なエネルギーが提供されない。しきい値周波数 $f 0$ は、そのエネルギーが仕事関数に等しい光子の周波数である。

\varphi =hf_{0}.

$f$ が $f 0$ より大きい場合、エネルギー $hf$ は電子を取り除くのに十分である。放出された電子の運動エネルギー $E K$ は最大で、光子のエネルギーから電子を金属から取り除くのに必要なエネルギーを引いたものに等しくなる。

E_{K}=hf-\varphi =h(f-f_{0}).

アインシュタインの光の説明は粒子で構成されており、プランクの量子化エネルギーの概念を拡張したものである。これは特定の周波数 $f$ の単一光子が不変量のエネルギー $hf$ を提供するというものである。言い換えると、個々の光子は多かれ少なかれエネルギーを供給しうるが、それはその周波数にのみ依存する。自然界では単一光子に遭遇することは滅多にない。19世紀に利用可能な太陽や放出源は毎秒膨大な数の光子を放出するため、各光子により運ばれるエネルギーの重要性は明らかではなかった。個々の光の単位に含まれるエネルギーはそれらの周波数に依存するというアインシュタインの考えは直感に反しているように見えた実験結果を説明することを可能にした。しかし、光子は粒子であるが、それでも周波数の波のような性質を持っていると説明されていた。実際、粒子としての光の説明は不十分であり、その波動のような性質は依然として必要である^[13]^{[note 4]}。

光を量子化した結果

電磁放射の周波数と各光子のエネルギーとの関係は、紫外線が日焼けを引き起こす可能性があり、可視光または赤外線ではそうでない理由である。紫外線の光子は日焼けで生じるような細胞の損傷に寄与するのに十分な量のエネルギーを供給する。赤外線の光子はエネルギーが小さく肌を温めるのに十分なだけである。したがって、赤外線ランプは広い表面を温めることができ、おそらく寒い部屋で人々を快適に保つのに十分な大きさであるが、誰も日焼けにすることはできない^[15]。

同じ周波数の全ての光子は同じエネルギーを有し、異なる周波数の全ての光子は比例して（次数1、 $E photon = hf$ ）異なるエネルギーを有する^[16]。ただし、光子により与えられるエネルギーは任意の周波数で不変であるが、光を吸収する前の光電装置内の電子の初期エネルギー状態は必ずしも均一ではない。個々の電子の場合、異常な結果が生じることがある。例えば、光電装置の平衡準位を超えてすでに励起された電子は、特徴的でない低い周波数の照明を吸収したときに放出される可能性がある。しかし、統計的には光電装置の特徴的な振る舞いは平衡準位にある電子の大部分の動作を反映している。この点は、量子力学における個々の粒子の研究と古典物理学における質量粒子の研究との違いを理解する一助となる^[要出典]。

物質の量子化: 原子のボーアモデル

20世紀が明けるまでに、証拠には小さくて密で正に帯電した原子核を取り巻く負に帯電した電子の拡散雲を有する原子のモデルが必要であった。これらの特性は太陽の周りを回る惑星のように、電子が原子核を周回するモデルを示唆した^{[note 5]}。しかし、このモデルの原子は不安定であることが知られていた。古典理論によれば、周回する電子は求心加速度を受けており、電磁放射を放出する必要がある。エネルギーが失われると、原子核に向かってらせん状になり、ほんの一瞬で原子核と衝突してしまう。

2番目の関連する謎は、原子の放出スペクトルであった。気体が熱されると、離散的な周波数でのみ発光する。例えば、水素により放出される可視光は、次図に示すように4つの異なる色からなる。異なる周波数での光の強度も異なる。対照的に、白色光は可視光の周波数の全範囲にわたる連続発光からなる。19世紀の終わりまでに、バルマーの公式として知られる単純な規則は、異なる線の周波数が互いにどのように関連するのかを示していたが、これがなぜであるかを説明したり、強度について予測したりすることはなかった。この式はその時点では観測されていなかった紫外線と赤外線のいくつかのさらなるスペクトル線を予測した。これらの線は後に実験的に観測され、式の値の信頼性を高めた。

水素の放出スペクトル。水素気体は励起されると、可視スペクトルの4つの異なる色（スペクトル線）と、赤外線および紫外線の多数の線で光を発する。

水素の放出スペクトルを表す式

1885年、スイスの数学者ヨハン・ヤコブ・バルマーは水素の可視スペクトルの各波長 $λ$ が次式により整数 $n$ に関連していることを発見した。

\lambda =B\left({\frac {n^{2}}{n^{2}-4}}\right)\qquad \qquad n=3,4,5,6

ここで $B$ はバルマーが決定した定数であり364.56 nmである。

1888年、ヨハネス・リュードベリはバルマーの式を一般化し、説明的有用性を大きくした。彼は、今日リュードベリの式として知られている式に従って、 $λ$ が2つの整数 $n$ と $m$ に関連していると予測した^[17]。

{\frac {1}{\lambda }}=R\left({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}}\right),

ここで R はリュードベリ定数であり0.0110 nm⁻¹に等しい。また、n は m より大きい。

リュードベリの式は、 $m = 2$ および $n = 3, 4, 5, 6$ とすることにより水素の4つの可視光の波長を説明する。放出スペクトルのさらなる波長も予測する。 $m = 1$ および $n > 1$ では放出スペクトルは特定の紫外線波長を含んでおり、 $m = 3$ および $n > 3$ では特定の赤外線波長を含む。これらの波長の実験は20年後に行われた。1908年にフリードリッヒ・パッシェンは予測された赤外線波長のいくつかを発見し、1914年にセオドア・ライマンが予測された紫外線波長のいくつかを発見した^[17]。

バルマーの式とリュードベリの式はどちらも整数を含む。これは現代の用語を使えば、原子のいくつかの特性が量子化されていることを意味する。この記事の残りの部分で示すように、この特性が何であるか、そしてなぜそれが量子化されたのかを正確に理解することが、量子力学の開発の主要な部分であった。

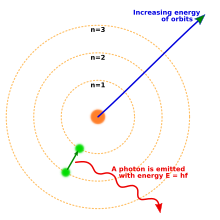
1913年、ニールス・ボーアは量子化された電子軌道を含む原子の新たなモデルを提案した。このモデルでは、惑星が太陽の周りを周回するのと同じように電子が原子核を周回するが、特定の軌道にのみいることが許され、任意の距離を周回することはできない^[18]。原子がエネルギーを放出（または吸収）したとき、古典力学から予想されるように、電子は原子核の周りのある軌道から別の軌道へと連続的な軌道で移動しない。代わりに、電子はある軌道から別の軌道に瞬時に飛び移り、放出された光を光子の形で放出する^[19]。各元素から放出される光子のとりうるエネルギーは、軌道間のエネルギーの差により決定されるため、各元素の放出スペクトルには多数の線が含まれる^[20]。

軌道が従わなければならない規則について1つの単純な過程から始めて、ボーアモデルは水素の放出スペクトルで観測されたスペクトル線を以前から知られている定数に関連付けることができた。ボーアのモデルでは、電子が連続的にエネルギーを放出して原子核に衝突することは許されておらず、許容された最も近い軌道に入ると電子は永久に安定である。ボーアのモデルは軌道をそのように量子化する必要がある理由を説明していなかったし、1以上の電子を持つ原子を正確に予測することも、一部のスペクトル線が他のスペクトル線よりも明るい理由を説明することができなかった。

ボーアモデルのいくつかの基本的な仮定はすぐに間違っていることが証明されたが、放出スペクトルの離散的な線は量子化されている原子の電子のいくつかの特性によるものであるという重要な結果は正しかった。電子が実際に振る舞う方法は、ボーアの原子とも、そして我々が日常的に経験する世界で見ているものとも大きく異なる。この原子の現代的な量子力学モデルについては以下で説明する。

ボーアモデルのより詳しい説明

ボーアは電子の角運動量 $L$ が量子化されると理論化した。

L=n{\frac {h}{2\pi }}=n\hbar

ここで $n$ は整数であり、 $h$ はプランク定数である。この仮定から始めてクーロンの法則と円運動の方程式は、 $n$ 単位の角運動量を持つ電子が次式で与えられる距離 $r$ で陽子を周回することを示す。

r={\frac {n^{2}h^{2}}{4\pi ^{2}k_{e}me^{2}}}

,

ここで $k e$ はクーロン定数であり、 $m$ は電子の質量であり、 $e$ は電子の電荷である。より平易に書くと

r=n^{2}a_{0},\!

となる。ここで $a 0$ はボーア半径と呼ばれ、0.0529 nmに等しい。ボーア半径は許容される最小軌道の半径である。

また、電子のエネルギー^{[note 6]}は次のように計算することができる。

E=-{\frac {k_{\mathrm {e} }e^{2}}{2a_{0}}}{\frac {1}{n^{2}}}

.

よって、角運動量が量子化されているというボーアの仮定は、電子が原子核の周りの特定の軌道にのみいることができ、特定のエネルギーしか有することができないことを意味する。これらの制約の結果、電子は原子核に衝突しない。電子は連続的にはエネルギーを放出できず、a₀（ボーア半径）よりも原子核に近づくことはできない。

電子は、元の軌道からより低い軌道に瞬時に飛び移ることでエネルギーを失う。余ったエネルギーは光子の形で放出される。逆に、光子を吸収する電子はエネルギーを得るため、原子核からより高い軌道に飛び移る。

光る水素原子からの各光子は、半径 $r n$ のより高い軌道から半径 $r m$ のより低い軌道に移動する電子によるものである。この光子のエネルギー $E γ$ は電子のエネルギー $E n$ と $E m$ の差である。

E_{\gamma }=E_{n}-E_{m}={\frac {k_{\mathrm {e} }e^{2}}{2a_{0}}}\left({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}}\right)

プランクの式は、式 $E γ = hc / λ$ により光子のエネルギーがその波長に関連していることを示しているため、放出できる光の波長は次式で与えられる。

{\frac {1}{\lambda }}={\frac {k_{\mathrm {e} }e^{2}}{2a_{0}hc}}\left({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}}\right).

この式はリュードベリの式と同じ形式であり、定数 $R$ は次式で与えられるべきであると予測する。

R={\frac {k_{\mathrm {e} }e^{2}}{2a_{0}hc}}.

したがって、原子のボーアモデルは、基本定数の観点から水素の放出スペクトルを予測できる^{[note 7]}。しかし、多電子原子を正確に予測したり、一部のスペクトル線が他のスペクトル線よりも明るい理由を説明したりすることはできなかった。

粒子と波動の二重性

→詳細は「粒子と波動の二重性」を参照

光が波のような性質と粒子のような性質の両方を持っているように、物質も波のような性質を持っている^[21]。

波として振る舞う物質は、最初に電子について実験的に実証された。電子線は光線や水の波のように回折を示すことができる^{[note 8]}。同様の波のような現象は、後に原子や分子でも示された。

任意の物体に関連する波長 λ は、プランク定数 h を介して運動量 p に関連する^[22]^[23]。

p={\frac {h}{\lambda }}.

ド・ブロイ仮説と呼ばれるこの関係式は、すべての種類の物質に当てはまり、全ての物質は粒子と波動の両方の性質を示す。

波動と粒子の二重性の概念は、「粒子」の古典的な概念も「波動」の古典的な概念も、光子または物質といった量子スケールの物体の振る舞いを完全に説明することはできないことを意味する。波動と粒子の二重性は量子物理学の相補性の原理の一例である^[24]^[25]^[26]^[27]^[28]。波動と粒子の二重性のエレガントな例である二重スリット実験については以下の節で説明する。

二重スリット実験

→詳細は「二重スリット実験」を参照

波動と粒子の二重性を実証する古典的な粒子、波、および量子粒子の二重スリット実験

1803年に最初にトマス・ヤングが最初に行い^[29]、10年後にオーギュスタン・ジャン・フレネルが行った^[29]二重スリット実験において、光線は2つの間隔の狭いスリットを通って導かれ、スクリーン上に明帯と暗帯の干渉パターンを生成する。スリットの1つが覆われていると、素朴には干渉による縞の強度がどこでも半分になると予想されるかもしれない。実際にはずっと単純なパターンが見られ、これは開いたスリットの正反対の回折パターンである。水の波でも同じ振る舞いが見られるため、二重スリット実験は光の波の性質を実証したものと見なされた。

電子、原子、さらにはそれより大きな分子を使用した二重スリット実験が行われており^[30]^[31]、同じタイプの干渉パターンが見られる。したがって、全ての物質が粒子と波動の両方の性質を持っていることが実証されている。

光源の強度を下げて1度に1つの粒子（光子や電子など）だけが装置を通過する場合にも、同じ干渉パターンが時間の経過とともに生じる。量子粒子は二重スリットを通過するときは波として振る舞うが、検出されるときは粒子として振る舞う。これは量子相補性の典型的な特徴である。量子粒子は波のような性質を測定する実験では波として振る舞い、粒子のような性質を測定する実験では粒子のように振る舞う。個々の粒子が表示される検出器のスクリーン上の点はランダム過程の結果である。ただし、多くの個々の粒子の分布パターンは、波により生成される回折パターンと似る。

ボーアモデルへの適用

ド・ブロイは、原子核の周りの軌道にある電子が波のような特性を持つと考えることができることを示すことによって、原子のボーアモデルを拡張しました。特に、電子は原子核の周りで定在波を許容する状況でのみ観測される。定在波の例は、両端が固定されて振動させることができるバイオリンの弦である。弦楽器によって生成された波は、その場で振動しているように見え、上下の動きで山から谷へと移動する。定在波の波長は、振動する物体の長さと境界条件に関係する。たとえば、バイオリンの弦は両端が固定されているため、波長 ${\frac {2l}{n}}$ （l は長さ、n は正の整数）の定在波を生じさせる。ド・ブロイは、許容される電子軌道は、軌道の円周が波長の整数倍になる軌道であることを提案した。したがって、電子の波長は、原子核から特定の距離のボーア軌道のみが可能であることを決定する。同様に、原子核から特定の値よりも小さい距離では、軌道を確立することは不可能である。原子核からの距離が最小な可能な距離はボーア半径と呼ばれる^[32]。

ド・ブロイによる量子的事象の扱いは、シュレーディンガーが量子論的事象を記述するための波動方程式の構築に取り掛かる上での出発点として役立った。

スピン

→詳細は「スピン角運動量」を参照

→「シュテルン＝ゲルラッハの実験」も参照

シュテルン＝ゲルラッハの実験における量子スピン vs 古典磁石

1922年、オットー・シュテルンとヴァルター・ゲルラッハは、銀原子を発射し、不均一な磁場を通した。その北の極に対して、上向き、下向き、またはその間のどこかで、古典力学においては、磁場を通して発射された磁石は、上向きまたは下向きに小さなまたは大きな距離、偏向する可能性がある。シュテルンとゲルラッハが発射して磁場を通した原子は同じように振る舞った。ただし、磁石は可変距離偏向できるが、原子は常に上または下に一定の距離だけ偏向する。これは、磁石の向きに対応する原子の特性を、任意の角度から自由に選択するのではなく、2つの値（上または下）のいずれかをとり量子化する必要があることを意味する。

ラルフ・クローニッヒは、原子や電子などの粒子が、軸を中心に回転または「回転」するかのように振る舞うという理論を考案しました。スピンは失われた磁気モーメントを説明し[明確化が必要]、同じ軌道にある2つの電子が反対方向に「スピン」した場合に異なる量子状態を占めることを可能にし、排除原理を満たします。量子数は、スピンの意味（正または負）を表しています。

Ralph Kronig originated the theory that particles such as atoms or electrons behave as if they rotate, or "spin", about an axis. Spin would account for the missing magnetic moment,^[要説明] and allow two electrons in the same orbital to occupy distinct quantum states if they "spun" in opposite directions, thus satisfying the exclusion principle. The quantum number represented the sense (positive or negative) of spin.

The choice of the orientation of the magnetic field used in the Stern–Gerlach experiment is arbitrary. In the animation shown here, the field is vertical and so the atoms are deflected either up or down. If the magnet is rotated a quarter turn, the atoms are deflected either left or right. Using a vertical field shows that the spin along the vertical axis is quantized, and using a horizontal field shows that the spin along the horizontal axis is quantized.

If instead of hitting a detector screen, one of the beams of atoms coming out of the Stern–Gerlach apparatus is passed into another (inhomogeneous) magnetic field oriented in the same direction, all of the atoms are deflected the same way in this second field. However, if the second field is oriented at 90° to the first, then half of the atoms are deflected one way and half the other so that the atom's spin about the horizontal and vertical axes are independent of each other. However, if one of these beams (e.g. the atoms that were deflected up then left) is passed into a third magnetic field, oriented the same way as the first, half of the atoms go one way and half the other, even though they all went in the same direction originally. The action of measuring the atoms' spin concerning a horizontal field has changed their spin concerning a vertical field.

The Stern–Gerlach experiment demonstrates several important features of quantum mechanics:

A feature of the natural world has been demonstrated to be quantized, and able to take only certain discrete values.
Particles possess an intrinsic angular momentum that is closely analogous to the angular momentum of a classically spinning object.
Measurement changes the system being measured in quantum mechanics. Only the spin of an object in one direction can be known, and observing the spin in another direction destroys the original information about the spin.
Quantum mechanics is probabilistic: whether the spin of any individual atom sent into the apparatus is positive or negative is random.

Development of modern quantum mechanics

In 1925, Werner Heisenberg attempted to solve one of the problems that the Bohr model left unanswered, explaining the intensities of the different lines in the hydrogen emission spectrum. Through a series of mathematical analogies, he wrote out the quantum-mechanical analog for the classical computation of intensities.^[33] Shortly afterward, Heisenberg's colleague Max Born realized that Heisenberg's method of calculating the probabilities for transitions between the different energy levels could best be expressed by using the mathematical concept of matrices.^{[note 9]}

In the same year, building on de Broglie's hypothesis, Erwin Schrödinger developed the equation that describes the behavior of a quantum-mechanical wave.^[34] The mathematical model, called the Schrödinger equation after its creator, is central to quantum mechanics, defines the permitted stationary states of a quantum system, and describes how the quantum state of a physical system changes in time.^[35] The wave itself is described by a mathematical function known as a "wave function". Schrödinger said that the wave function provides the "means for predicting the probability of measurement results".^[36]

Schrödinger was able to calculate the energy levels of hydrogen by treating a hydrogen atom's electron as a classical wave, moving in a well of the electrical potential created by the proton. This calculation accurately reproduced the energy levels of the Bohr model.

In May 1926, Schrödinger proved that Heisenberg's matrix mechanics and his own wave mechanics made the same predictions about the properties and behavior of the electron; mathematically, the two theories had an underlying common form. Yet the two men disagreed on the interpretation of their mutual theory. For instance, Heisenberg accepted the theoretical prediction of jumps of electrons between orbitals in an atom,^[37] but Schrödinger hoped that a theory based on continuous wave-like properties could avoid what he called (as paraphrased by Wilhelm Wien) "this nonsense about quantum jumps".^[38] In the end, Heisenberg's approach won out, and quantum jumps were confirmed.^[39]

Copenhagen interpretation

→詳細は「Copenhagen interpretation」を参照

Bohr, Heisenberg, and others tried to explain what these experimental results and mathematical models really mean. Their description, known as the Copenhagen interpretation of quantum mechanics, aimed to describe the nature of reality that was being probed by the measurements and described by the mathematical formulations of quantum mechanics.

The main principles of the Copenhagen interpretation are:

A system is completely described by a wave function, usually represented by the Greek letter $\psi$ ("psi"). (Heisenberg)
How $\psi$ changes over time is given by the Schrödinger equation.^[要説明]
The description of nature is essentially probabilistic. The probability of an event—for example, where on the screen a particle shows up in the double-slit experiment—is related to the square of the absolute value of the amplitude of its wave function. (Born rule, due to Max Born, which gives a physical meaning to the wave function in the Copenhagen interpretation: the probability amplitude)
It is not possible to know the values of all of the properties of the system at the same time; those properties that are not known with precision must be described by probabilities. (Heisenberg's uncertainty principle)
Matter, like energy, exhibits a wave-particle duality. An experiment can demonstrate the particle-like properties of matter, or its wave-like properties; but not both at the same time. (Complementarity principle due to Bohr)
Measuring devices are essentially classical devices and measure classical properties such as position and momentum.
The quantum mechanical description of large systems should closely approximate the classical description. (Correspondence principle of Bohr and Heisenberg)

Various consequences of these principles are discussed in more detail in the following subsections.

Uncertainty principle

→詳細は「Uncertainty principle」を参照

Suppose it is desired to measure the position and speed of an object—for example, a car going through a radar speed trap. It can be assumed that the car has a definite position and speed at a particular moment in time. How accurately these values can be measured depends on the quality of the measuring equipment. If the precision of the measuring equipment is improved, it provides a result closer to the true value. It might be assumed that the speed of the car and its position could be operationally defined and measured simultaneously, as precisely as might be desired.

In 1927, Heisenberg proved that this last assumption is not correct.^[41] Quantum mechanics shows that certain pairs of physical properties, for example, position and speed, cannot be simultaneously measured, nor defined in operational terms, to arbitrary precision: the more precisely one property is measured, or defined in operational terms, the less precisely can the other. This statement is known as the uncertainty principle. The uncertainty principle is not only a statement about the accuracy of our measuring equipment but, more deeply, is about the conceptual nature of the measured quantities—the assumption that the car had simultaneously defined position and speed does not work in quantum mechanics. On a scale of cars and people, these uncertainties are negligible, but when dealing with atoms and electrons they become critical.^[42]

Heisenberg gave, as an illustration, the measurement of the position and momentum of an electron using a photon of light. In measuring the electron's position, the higher the frequency of the photon, the more accurate is the measurement of the position of the impact of the photon with the electron, but the greater is the disturbance of the electron. This is because from the impact with the photon, the electron absorbs a random amount of energy, rendering the measurement obtained of its momentum increasingly uncertain (momentum is velocity multiplied by mass), for one is necessarily measuring its post-impact disturbed momentum from the collision products and not its original momentum. With a photon of lower frequency, the disturbance (and hence uncertainty) in the momentum is less, but so is the accuracy of the measurement of the position of the impact.^[43]

At the heart of the uncertainty principle is not a mystery, but the simple fact that for any mathematical analysis in the position and velocity domains (Fourier analysis), achieving a sharper (more precise) curve in the position domain can only be done at the expense of a more gradual (less precise) curve in the speed domain, and vice versa. More sharpness in the position domain requires contributions from more frequencies in the speed domain to create the narrower curve, and vice versa. It is a fundamental tradeoff inherent in any such related or complementary measurements, but is only really noticeable at the smallest (Planck) scale, near the size of elementary particles.

The uncertainty principle shows mathematically that the product of the uncertainty in the position and momentum of a particle (momentum is velocity multiplied by mass) could never be less than a certain value, and that this value is related to Planck's constant.

Wave function collapse

→詳細は「Wave function collapse」を参照

Wave function collapse means that a measurement has forced or converted a quantum (probabilistic or potential) state into a definite measured value. This phenomenon is only seen in quantum mechanics rather than classical mechanics.

For example, before a photon actually "shows up" on a detection screen it can be described only with a set of probabilities for where it might show up. When it does appear, for instance in the CCD of an electronic camera, the time and space where it interacted with the device are known within very tight limits. However, the photon has disappeared in the process of being captured (measured), and its quantum wave function has disappeared with it. In its place, some macroscopic physical change in the detection screen has appeared, e.g., an exposed spot in a sheet of photographic film, or a change in electric potential in some cell of a CCD.

Eigenstates and eigenvalues

For a more detailed introduction to this subject, see Introduction to eigenstates

Because of the uncertainty principle, statements about both the position and momentum of particles can assign only a probability that the position or momentum has some numerical value. Therefore, it is necessary to formulate clearly the difference between the state of something indeterminate, such as an electron in a probability cloud, and the state of something having a definite value. When an object can definitely be "pinned-down" in some respect, it is said to possess an eigenstate.

In the Stern–Gerlach experiment discussed above, the spin of the atom about the vertical axis has two eigenstates: up and down. Before measuring it, we can only say that any individual atom has an equal probability of being found to have spin up or spin down. The measurement process causes the wavefunction to collapse into one of the two states.

The eigenstates of spin about the vertical axis are not simultaneously eigenstates of spin about the horizontal axis, so this atom has an equal probability of being found to have either value of spin about the horizontal axis. As described in the section above, measuring the spin about the horizontal axis can allow an atom that was spun up to spin down: measuring its spin about the horizontal axis collapses its wave function into one of the eigenstates of this measurement, which means it is no longer in an eigenstate of spin about the vertical axis, so can take either value.

The Pauli exclusion principle

→詳細は「Pauli exclusion principle」を参照

In 1924, Wolfgang Pauli proposed a new quantum degree of freedom (or quantum number), with two possible values, to resolve inconsistencies between observed molecular spectra and the predictions of quantum mechanics. In particular, the spectrum of atomic hydrogen had a doublet, or pair of lines differing by a small amount, where only one line was expected. Pauli formulated his exclusion principle, stating, "There cannot exist an atom in such a quantum state that two electrons within [it] have the same set of quantum numbers."^[44]

A year later, Uhlenbeck and Goudsmit identified Pauli's new degree of freedom with the property called spin whose effects were observed in the Stern–Gerlach experiment.

Application to the hydrogen atom

→詳細は「Atomic orbital model」を参照

Bohr's model of the atom was essentially a planetary one, with the electrons orbiting around the nuclear "sun". However, the uncertainty principle states that an electron cannot simultaneously have an exact location and velocity in the way that a planet does. Instead of classical orbits, electrons are said to inhabit atomic orbitals. An orbital is the "cloud" of possible locations in which an electron might be found, a distribution of probabilities rather than a precise location.^[44] Each orbital is three dimensional, rather than the two-dimensional orbit, and is often depicted as a three-dimensional region within which there is a 95 percent probability of finding the electron.^[45]

Schrödinger was able to calculate the energy levels of hydrogen by treating a hydrogen atom's electron as a wave, represented by the "wave function" $Ψ$ , in an electric potential well, $V$ , created by the proton. The solutions to Schrödinger's equation ^[要説明] are distributions of probabilities for electron positions and locations. Orbitals have a range of different shapes in three dimensions. The energies of the different orbitals can be calculated, and they accurately match the energy levels of the Bohr model.

Within Schrödinger's picture, each electron has four properties:

An "orbital" designation, indicating whether the particle-wave is one that is closer to the nucleus with less energy or one that is farther from the nucleus with more energy;
The "shape" of the orbital, spherical or otherwise;
The "inclination" of the orbital, determining the magnetic moment of the orbital around the $z$ -axis.
The "spin" of the electron.

The collective name for these properties is the quantum state of the electron. The quantum state can be described by giving a number to each of these properties; these are known as the electron's quantum numbers. The quantum state of the electron is described by its wave function. The Pauli exclusion principle demands that no two electrons within an atom may have the same values of all four numbers.

The first property describing the orbital is the principal quantum number, $n$ , which is the same as in Bohr's model. $n$ denotes the energy level of each orbital. The possible values for $n$ are integers:

n=1,2,3\ldots

The next quantum number, the azimuthal quantum number, denoted $l$ , describes the shape of the orbital. The shape is a consequence of the angular momentum of the orbital. The angular momentum represents the resistance of a spinning object to speeding up or slowing down under the influence of external force. The azimuthal quantum number represents the orbital angular momentum of an electron around its nucleus. The possible values for $l$ are integers from 0 to $n - 1$ (where $n$ is the principal quantum number of the electron):

l=0,1,\ldots ,n-1.

The shape of each orbital is usually referred to by a letter, rather than by its azimuthal quantum number. The first shape ( $l$ =0) is denoted by the letter $s$ (a mnemonic being "sphere"). The next shape is denoted by the letter $p$ and has the form of a dumbbell. The other orbitals have more complicated shapes (see atomic orbital), and are denoted by the letters $d$ , $f$ , $g$ , etc.

The third quantum number, the magnetic quantum number, describes the magnetic moment of the electron, and is denoted by $m l$ (or simply m). The possible values for $m l$ are integers from $- l$ to $l$ (where $l$ is the azimuthal quantum number of the electron):

m_{l}=-l,-(l-1),\ldots ,0,1,\ldots ,l.

The magnetic quantum number measures the component of the angular momentum in a particular direction. The choice of direction is arbitrary; conventionally the z-direction is chosen.

The fourth quantum number, the spin quantum number (pertaining to the "orientation" of the electron's spin) is denoted $m s$ , with values +1⁄2 or −1⁄2.

The chemist Linus Pauling wrote, by way of example:

In the case of a helium atom with two electrons in the 1s orbital, the Pauli Exclusion Principle requires that the two electrons differ in the value of one quantum number. Their values of $n$ , $l$ , and $m l$ are the same. Accordingly they must differ in the value of $m s$ , which can have the value of +1⁄2 for one electron and −1⁄2 for the other."^[44]

It is the underlying structure and symmetry of atomic orbitals, and the way that electrons fill them, that leads to the organization of the periodic table. The way the atomic orbitals on different atoms combine to form molecular orbitals determines the structure and strength of chemical bonds between atoms.

Dirac wave equation

→詳細は「Dirac equation」を参照

In 1928, Paul Dirac extended the Pauli equation, which described spinning electrons, to account for special relativity. The result was a theory that dealt properly with events, such as the speed at which an electron orbits the nucleus, occurring at a substantial fraction of the speed of light. By using the simplest electromagnetic interaction, Dirac was able to predict the value of the magnetic moment associated with the electron's spin and found the experimentally observed value, which was too large to be that of a spinning charged sphere governed by classical physics. He was able to solve for the spectral lines of the hydrogen atom and to reproduce from physical first principles Sommerfeld's successful formula for the fine structure of the hydrogen spectrum.

Dirac's equations sometimes yielded a negative value for energy, for which he proposed a novel solution: he posited the existence of an antielectron and a dynamical vacuum. This led to the many-particle quantum field theory.

Quantum entanglement

→詳細は「Quantum entanglement」を参照

Superposition of two quantum characteristics, and two resolution possibilities.

The Pauli exclusion principle says that two electrons in one system cannot be in the same state. Nature leaves open the possibility, however, that two electrons can have both states "superimposed" over each of them. Recall that the wave functions that emerge simultaneously from the double slits arrive at the detection screen in a state of superposition. Nothing is certain until the superimposed waveforms "collapse". At that instant, an electron shows up somewhere in accordance with the probability that is the square of the absolute value of the sum of the complex-valued amplitudes of the two superimposed waveforms. The situation there is already very abstract. A concrete way of thinking about entangled photons, photons in which two contrary states are superimposed on each of them in the same event, is as follows:

Imagine that we have two color-coded states of photons: one state labeled blue and another state labeled red. Let the superposition of the red and the blue state appear (in imagination) as a purple state. We consider a case in which two photons are produced as the result of one single atomic event. Perhaps they are produced by the excitation of a crystal that characteristically absorbs a photon of a certain frequency and emits two photons of half the original frequency. In this case, the photons are interconnected via their shared origin in a single atomic event. This setup results in superimposed states of the photons. So the two photons come out purple. If the experimenter now performs some experiment that determines whether one of the photons is either blue or red, then that experiment changes the photon involved from one having a superposition of blue and red characteristics to a photon that has only one of those characteristics. The problem that Einstein had with such an imagined situation was that if one of these photons had been kept bouncing between mirrors in a laboratory on earth, and the other one had traveled halfway to the nearest star when its twin was made to reveal itself as either blue or red, that meant that the distant photon now had to lose its purple status too. So whenever it might be investigated after its twin had been measured, it would necessarily show up in the opposite state to whatever its twin had revealed.

In trying to show that quantum mechanics was not a complete theory, Einstein started with the theory's prediction that two or more particles that have interacted in the past can appear strongly correlated when their various properties are later measured. He sought to explain this seeming interaction classically, through their common past, and preferably not by some "spooky action at a distance". The argument is worked out in a famous paper, Einstein, Podolsky, and Rosen (1935; abbreviated EPR) setting out what is now called the EPR paradox. Assuming what is now usually called local realism, EPR attempted to show from quantum theory that a particle has both position and momentum simultaneously, while according to the Copenhagen interpretation, only one of those two properties actually exists and only at the moment that it is being measured. EPR concluded that quantum theory is incomplete in that it refuses to consider physical properties that objectively exist in nature. (Einstein, Podolsky, & Rosen 1935 is currently Einstein's most cited publication in physics journals.) In the same year, Erwin Schrödinger used the word "entanglement" and declared: "I would not call that one but rather the characteristic trait of quantum mechanics."^[46] Ever since Irish physicist John Stewart Bell theoretically and experimentally disproved the "hidden variables" theory of Einstein, Podolsky, and Rosen, most physicists have accepted entanglement as a real phenomenon.^[47] However, there is some minority dispute.^[48] The Bell inequalities are the most powerful challenge to Einstein's claims.

Quantum field theory

→詳細は「Quantum field theory」を参照

The idea of quantum field theory began in the late 1920s with British physicist Paul Dirac, when he attempted to quantize the energy of the electromagnetic field; just like in quantum mechanics the energy of an electron in the hydrogen atom was quantized. Quantization is a procedure for constructing a quantum theory starting from a classical theory.

Merriam-Webster defines a field in physics as "a region or space in which a given effect (such as magnetism) exists".^[49] Other effects that manifest themselves as fields are gravitation and static electricity.^[50] In 2008, physicist Richard Hammond wrote:

Sometimes we distinguish between quantum mechanics (QM) and quantum field theory (QFT). QM refers to a system in which the number of particles is fixed, and the fields (such as the electromechanical field) are continuous classical entities. QFT ... goes a step further and allows for the creation and annihilation of particles ...

He added, however, that quantum mechanics is often used to refer to "the entire notion of quantum view".^[51]^:108

In 1931, Dirac proposed the existence of particles that later became known as antimatter.^[52] Dirac shared the Nobel Prize in Physics for 1933 with Schrödinger "for the discovery of new productive forms of atomic theory".^[53]

On its face, quantum field theory allows infinite numbers of particles and leaves it up to the theory itself to predict how many and with which probabilities or numbers they should exist. When developed further, the theory often contradicts observation, so that its creation and annihilation operators can be empirically tied down.^[要説明] Furthermore, empirical conservation laws such as that of mass–energy suggest certain constraints on the mathematical form of the theory, which are mathematically speaking finicky. The latter fact makes quantum field theories difficult to handle, but has also led to further restrictions on admissible forms of the theory; the complications are mentioned below under the rubric of renormalization.

Quantum electrodynamics

→詳細は「Quantum electrodynamics」を参照

Quantum electrodynamics (QED) is the name of the quantum theory of the electromagnetic force. Understanding QED begins with understanding electromagnetism. Electromagnetism can be called "electrodynamics" because it is a dynamic interaction between electrical and magnetic forces. Electromagnetism begins with the electric charge.

Electric charges are the sources of and create, electric fields. An electric field is a field that exerts a force on any particles that carry electric charges, at any point in space. This includes the electron, proton, and even quarks, among others. As a force is exerted, electric charges move, a current flows, and a magnetic field is produced. The changing magnetic field, in turn, causes electric current (often moving electrons). The physical description of interacting charged particles, electrical currents, electrical fields, and magnetic fields are called electromagnetism.

In 1928 Paul Dirac produced a relativistic quantum theory of electromagnetism. This was the progenitor to modern quantum electrodynamics, in that it had essential ingredients of the modern theory. However, the problem of unsolvable infinities developed in this relativistic quantum theory. Years later, renormalization largely solved this problem. Initially viewed as a suspect, provisional procedure by some of its originators, renormalization eventually was embraced as an important and self-consistent tool in QED and other fields of physics. Also, in the late 1940s Feynman's diagrams depicted all possible interactions on a given event. The diagrams showed in particular that the electromagnetic force is the exchange of photons between interacting particles.^[54]

The Lamb shift is an example of a quantum electrodynamics prediction that has been experimentally verified. It is an effect whereby the quantum nature of the electromagnetic field makes the energy levels in an atom or ion deviate slightly from what they would otherwise be. As a result, spectral lines may shift or split.

Similarly, within a freely propagating electromagnetic wave, the current can also be just an abstract displacement current, instead of involving charge carriers. In QED, its full description makes essential use of short-lived virtual particles. There, QED again validates an earlier, rather mysterious concept.

Standard Model

→詳細は「Standard Model」を参照

In the 1960s physicists realized that QED broke down at extremely high energies.^[要出典] From this inconsistency the Standard Model of particle physics was discovered, which remedied the higher energy breakdown in theory. It is another extended quantum field theory that unifies the electromagnetic and weak interactions into one theory. This is called the electroweak theory.

Additionally, the Standard Model contains^[要出典] a high energy unification of the electroweak theory with the strong force, described by quantum chromodynamics. It also postulates a connection with gravity as yet another gauge theory, but the connection is as of 2015 still poorly understood. The theory's successful prediction of the Higgs particle to explain inertial mass was confirmed by the Large Hadron Collider,^[55] and thus the Standard model is now considered the basic and more or less complete description of particle physics as we know it.

Interpretations

→詳細は「Interpretations of quantum mechanics」を参照

The physical measurements, equations, and predictions pertinent to quantum mechanics are all consistent and hold a very high level of confirmation. However, the question of what these abstract models say about the underlying nature of the real world has received competing answers. These interpretations are widely varying and sometimes somewhat abstract. For instance, the Copenhagen interpretation states that before a measurement, statements about a particles' properties are completely meaningless, while in the Many-worlds interpretation describes the existence of a multiverse made up of every possible universe.^[56]

Applications

→詳細は「Quantum mechanics: applications」を参照

Applications of quantum mechanics include the laser, the transistor, the electron microscope, and magnetic resonance imaging. A special class of quantum mechanical applications is related to macroscopic quantum phenomena such as superfluid helium and superconductors. The study of semiconductors led to the invention of the diode and the transistor, which are indispensable for modern electronics.

In even the simple light switch, quantum tunneling is absolutely vital, as otherwise the electrons in the electric current could not penetrate the potential barrier made up of a layer of oxide. Flash memory chips found in USB drives also use quantum tunneling, to erase their memory cells.^[57]

注

^ 熱放射の実験的測定のいくつかを記述できる数式がいくつか作られた。放射が最も強くなる波長が温度によりどのように変化するかはヴィーンの変位則により与えられ、単位面積当たりに放出される全体的なエネルギーはシュテファン＝ボルツマンの法則により与えられる。実験結果の最良の理論的説明はレイリー・ジーンズの法則であった。これは長波長（低周波数）では実験結果とよく一致するが、短波長（高周波数）ではほとんど一致しない。実際、短波長では、古典物理学はエネルギーが無限の速度で高温の物体から放出されると予測していた。明らかに間違っているこの結果は紫外破綻として知られている
^ 量子(quantum)という言葉はラテン語で「どれくらい」("how much")を意味する言葉に由来する（量(quantity)も同様）。プランクの調和振動子のエネルギーとして量子化されたものは、特定の値しかとることができない。例えば、ほとんどの国でお金は効果的に量子化されており、「お金の量子」は流通している最も額面の低い硬貨である。力学は、物体に対する力の作用を扱う科学の分野である。したがって、量子力学は特定の特性が量子化されている物体を処理する力学の一分野である。
^ 実際には、強度に依存する効果が存在する可能性があるが、非レーザー光源で実現可能な強度ではこれらの効果は観測することができない。
^ アインシュタインの光電効果の方程式は「光子」の概念を必要せずに導出され、説明することができる。つまり、物質中の電子が量子力学の法則によって扱われる限り、電磁放射は古典的な電磁波として扱うことができる。結果は電子放出率とその角度分布の両方について、熱光源（太陽、白熱灯など）に対して定量的に正しいものである。この点の詳細については^[14]参照
^ 原子の古典的なモデルは惑星モデル、またはラザフォードモデルと呼ばれる。この名は核の存在を最初に実証したガイガー＝マースデンの実験に基づいて1911年に提案したアーネスト・ラザフォードにちなむ。
^ この場合、電子のエネルギーは、その運動エネルギーと位置エネルギーの和である。電子は原子核の周りの実際の運動により運動エネルギーを有し、原子核との電磁相互作用により位置エネルギーを有し。
^ このモデルは原子核と単一の電子（つまり1つの電子のみを含むHe⁺ や O⁷⁺ などのイオン）で構成される任意の軽の放出スペクトルを考慮して簡単に変更できるが、中性のヘリウムなど2つの電子を有する原子に拡張することはできない。
^ 電子回折はド・ブロイが仮説を発表してから3年後に初めて実証された。アバディーン大学で、ジョージ・パジェット・トムソンが電子線を金属薄膜に通し、ド・ブロイの仮説により予測されるような回折パターンを観測した。ベル研究所では、デイヴィソンとガーマーが結晶グリッドを通して電子線を導いた。ド・ブロイはその仮説により1929年にノーベル物理学賞を受賞した。トムソンとデイヴィソンは実験的研究によりノーベル物理学賞を共同受賞した。
^ For a somewhat more sophisticated look at how Heisenberg transitioned from the old quantum theory and classical physics to the new quantum mechanics, see Heisenberg's entryway to matrix mechanics.

出典

^ “Quantum Mechanics”. National Public Radio. 22 June 2016閲覧。
^ Kuhn, Thomas S. The Structure of Scientific Revolutions. Fourth ed. Chicago; London: The University of Chicago Press, 2012. Print.
^ “Introduction to Quantum Mechanics”. Socratease. 2017年9月15日時点のオリジナルよりアーカイブ。 Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ Feynman, Richard P. (1988). QED : the strange theory of light and matter (1st Princeton pbk., seventh printing with corrections. ed.). Princeton, NJ: Princeton University Press. pp. 10. ISBN 978-0691024172
^ This result was published (in German) as Planck, Max (1901). “Ueber das Gesetz der Energieverteilung im Normalspectrum”. Ann. Phys. 309 (3): 553–63. Bibcode: 1901AnP...309..553P. doi:10.1002/andp.19013090310. オリジナルの10 June 2012時点におけるアーカイブ。. . English translation: “On the Law of Distribution of Energy in the Normal Spectrum”. 18 April 2008時点のオリジナルよりアーカイブ。 Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ Francis Weston Sears (1958). Mechanics, Wave Motion, and Heat. Addison-Wesley. p. 537
^ “The Nobel Prize in Physics 1918”. Nobel Foundation. 2009年8月1日閲覧。
^ Kragh, Helge (1 December 2000). “Max Planck: the reluctant revolutionary”. PhysicsWorld.com. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ Einstein, Albert (1905). “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt”. Annalen der Physik 17 (6): 132–48. Bibcode: 1905AnP...322..132E. doi:10.1002/andp.19053220607. , translated into English as On a Heuristic Viewpoint Concerning the Production and Transformation of Light Archived 11 June 2009 at the Wayback Machine.. The term "photon" was introduced in 1926.
^ “Revival of the Wave Theory of Light in the Early Nineteenth-Century”. www.encyclopedia.com. 16 October 2018閲覧。
^ ^a ^b ^c ^d ^e Taylor, J. R.; Zafiratos, C. D.; Dubson, M. A. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. pp. 127–29. ISBN 0135897890
^ Hawking, Stephen (November 6, 2001) (英語). The Universe in a Nutshell. 55. Impey, C.D.. Bantam Spectra (April 2002発行). p. 80~. doi:10.1063/1.1480788. ISBN 978-0553802023. オリジナルのJuly 20, 2016時点におけるアーカイブ。 December 14, 2020閲覧。
^ Dicke, Robert Henry; Wittke, James P. (1960). Introduction to Quantum Mechanics. Addison-Wesley Publishing Company. p. 12. ISBN 978-0201015102
^ “The Photoelectric Effect Without Photons”. NTRS.NASA.gov. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ Jim Lucas: 'What Is Ultraviolet Light?', 15 September 2017, at livescience.com Accessed 27 December 2017
^ 'Two Equations Governing Light's Behavior: Part Two E = hν' at chemteam.info Accessed 27 December 2017
^ ^a ^b Taylor, J. R.; Zafiratos, C. D.; Dubson, M. A. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. pp. 147–48. ISBN 0135897890
^ McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. pp. 70–89, [89]. ISBN 1840465778
^ World Book.Inc (2007). “22” (英語). World Book Encyclopedia (Electronic reproduction). The World Book encyclopedia. 22 (3 ed.). Chicago, Illinois: World Book. p. 6. ISBN 978-0716601074. OCLC 894799866. オリジナルの2011時点におけるアーカイブ。 December 14, 2020閲覧。
^ Wittke, J.P; Dicke, R.H (June 1, 1961). “11”. In Holladay, W.G. (英語). Introduction to Quantum Mechanics (eBook). 16. Nashville, Tennessee: ADDISON WESLEY LONGMAN INC. January 1, 1978. p. 10. ASIN B000K3HWYO. doi:10.1063/1.3057610. ISBN 978-0201015102. OCLC 53473 December 14, 2020閲覧。
^ McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. pp. 110ff. ISBN 1840465778
^ Aczel, Amir D., Entanglement, pp. 51ff. (Penguin, 2003) ISBN 978-1551926476
^ McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. p. 114. ISBN 1840465778
^ Zettili, Nouredine (2009). Quantum Mechanics: Concepts and Applications. John Wiley and Sons. pp. 26–27. ISBN 978-0470026786
^ Selleri, Franco (2012). Wave-Particle Duality. Springer Science and Business Media. pp. 41. ISBN 978-1461533320
^ Podgorsak, Ervin B. (2013). Compendium to Radiation Physics for Medical Physicists. Springer Science and Business Media. pp. 88. ISBN 978-3642201868
^ Halliday, David; Resnick, Robert (2013). Fundamentals of Physics, 10th Ed.. John Wiley and Sons. pp. 1272. ISBN 978-1118230619
^ Myers, Rusty L. (2006). The Basics of Physics. Greenwood Publishing Group. pp. 172. ISBN 0313328579. "complementarity principle wave-particle duality."
^ ^a ^b Shamos, Morris H (1 January 1987). Great Experiments in Physics: Firsthand Accounts from Galileo to Einstein. Courier Corporation. p. 108
^ Merali, Zeeya (21 May 2015). “Quantum physics: What is really real?”. Nature: pp. 278–80. Bibcode: 2015Natur.521..278M. doi:10.1038/521278a 7 January 2017閲覧。
^ Eibenberger, Sandra (2013). “Matter–wave interference of particles selected from a molecular library with masses exceeding 10 000 amu”. Physical Chemistry Chemical Physics 15 (35): 14696–700. arXiv:1310.8343. Bibcode: 2013PCCP...1514696E. doi:10.1039/C3CP51500A. PMID 23900710. "[I]n a three-grating interferometer... We observe high-contrast quantum fringe patterns of molecules... having 810 atoms in a single particle."
^ McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. p. 87. ISBN 1840465778
^ Van der Waerden, B. L. (1967) (英語). Sources of Quantum Mechanics. Mineola, NY: Dover Publications. pp. 261–76. "Received 29 July 1925" See Werner Heisenberg's paper, "Quantum-Theoretical Re-interpretation of Kinematic and Mechanical Relations" pp. 261–76
^ Nobel Prize Organization. “Erwin Schrödinger – Biographical”. 28 March 2014閲覧。 “His great discovery, Schrödinger's wave equation, was made at the end of this epoch-during the first half of 1926.”
^ "Schrodinger Equation (Physics)", Encyclopædia Britannica
^ Erwin Schrödinger, "The Present Situation in Quantum Mechanics", p. 9. "This translation was originally published in Proceedings of the American Philosophical Society, 124, 323–38, and then appeared as Section I.11 of Part I of Quantum Theory and Measurement (J. A. Wheeler and W. H. Zurek, eds., Princeton University Press, NJ 1983). This paper can be downloaded here: Erwin Schrödinger. “A Translation of Schrödinger's "Cat Paradox Paper"”. 2010年11月13日時点のオリジナルよりアーカイブ。 Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ Heisenberg, W. (1955). The development of the interpretation of the quantum theory, pp. 12–29 in Niels Bohr and the Development of Physics: Essays dedicated to Niels Bohr on the occasion of his seventieth birthday, edited by Pauli, W. with the assistance of Rosenfeld, L. and Weisskopf, V., Pergamon, London, p. 13: "the single quantum jump ... is "factual" in nature".
^ W. Moore, Schrödinger: Life and Thought, Cambridge University Press (1989), p. 222. See p. 227 for Schrödinger's own words.
^ “Physicists finally get to see quantum jump with own eyes”. The New York Times. 30 November 2019閲覧。
^ “The Nobel Prize in Physics 1932”. NobelPrize.org. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ Heisenberg first published his work on the uncertainty principle in the leading German physics journal Zeitschrift für Physik: Heisenberg, W. (1927). “Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik”. Z. Phys. 43 (3–4): 172–98. Bibcode: 1927ZPhy...43..172H. doi:10.1007/BF01397280.
^ “The Nobel Prize in Physics 1932”. NobelPrize.org. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ "Uncertainty principle", Encyclopædia Britannica
^ ^a ^b ^c Pauling, Linus (1960). The Nature of the Chemical Bond (3rd ed.). Itahca, NY: Cornell University Press. p. 47. ISBN 0801403332 1 March 2016閲覧。
^ "Orbital (chemistry and physics)", Encyclopædia Britannica
^ E. Schrödinger, Proceedings of the Cambridge Philosophical Society, 31 (1935), p. 555, says: "When two systems, of which we know the states by their respective representation, enter into a temporary physical interaction due to known forces between them and when after a time of mutual influence the systems separate again, then they can no longer be described as before, viz., by endowing each of them with a representative of its own. I would not call that one but rather the characteristic trait of quantum mechanics."
^ David Kaiser, Is Quantum Entanglement Real?, The New York Times, Nov. 2014.
^ John G. Cramer. “Quantum Nonlocality and the Possibility of Superluminal Effects”. npl.washington.edu. 29 December 2010時点のオリジナルよりアーカイブ。 Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ "Mechanics", Merriam-Webster Online Dictionary
^ "Field", Encyclopædia Britannica
^ Richard Hammond, The Unknown Universe, New Page Books, 2008. ISBN 978-1601630032
^ “Featured Physicists – Paul Dirac 1902–1984”. www.physicalworld.org. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ “The Nobel Prize in Physics 1933”. Nobel Foundation. 2007年11月24日閲覧。
^ “Exchange Particles”. hyperphysics.phy-astr.gsu.edu. 16 October 2018閲覧。
^ “Ten years of Large Hadron Collider discoveries below Swiss countryside are just the start of decoding the universe”. www.thelocal.ch (5 October 2018). 16 October 2018閲覧。
^ “Copenhagen Interpretation”. abyss.uoregon.edu. 16 October 2018閲覧。
^ Durrani, Z. A. K.; Ahmed, H. (2008). Vijay Kumar. ed. Nanosilicon. Elsevier. p. 345. ISBN 978-0080445281

書誌情報

Bernstein, Jeremy (2005). “Max Born and the quantum theory”. American Journal of Physics 73 (11): 999–1008. Bibcode: 2005AmJPh..73..999B. doi:10.1119/1.2060717.
Beller, Mara (2001). Quantum Dialogue: The Making of a Revolution. University of Chicago Press
Bohr, Niels (1958). Atomic Physics and Human Knowledge. John Wiley & Sons]. ISBN 0486479285. OCLC 530611
de Broglie, Louis (1953). The Revolution in Physics. Noonday Press. LCCN 53-10401
Bronner, Patrick; Strunz, Andreas; Silberhorn, Christine; Meyn, Jan-Peter (2009). “Demonstrating quantum random with single photons”. European Journal of Physics 30 (5): 1189–1200. Bibcode: 2009EJPh...30.1189B. doi:10.1088/0143-0807/30/5/026.
Einstein, Albert (1934). Essays in Science. Philosophical Library. ISBN 0486470113. LCCN 55-3947
Feigl, Herbert; Brodbeck, May (1953). Readings in the Philosophy of Science. Appleton-Century-Crofts. ISBN 0390304883. LCCN 53-6438
Feynman, Richard P. (1949). “Space-Time Approach to Quantum Electrodynamics”. Physical Review 76 (6): 769–89. Bibcode: 1949PhRv...76..769F. doi:10.1103/PhysRev.76.769. ^{[リンク切れ]}
Feynman, Richard P. (1990). QED, The Strange Theory of Light and Matter. Penguin Books. ISBN 978-0140125054
Fowler, Michael (1999). The Bohr Atom. University of Virginia ^[要ISBN]
Heisenberg, Werner (1958). Physics and Philosophy. Harper and Brothers. ISBN 0061305499. LCCN 99-10404
Lakshmibala, S. (2004). “Heisenberg, Matrix Mechanics and the Uncertainty Principle”. Resonance: Journal of Science Education 9 (8): 46–56. doi:10.1007/bf02837577.
Liboff, Richard L. (1992). Introductory Quantum Mechanics (2nd ed.) ^[要ISBN]
Lindsay, Robert Bruce; Margenau, Henry (1957). Foundations of Physics. Dover. ISBN 0918024188. LCCN 57-14416
McEvoy, J. P.; Zarate, Oscar (2004). Introducing Quantum Theory. ISBN 1874166374
Nave, Carl Rod (2005年). “Quantum Physics”. HyperPhysics. Georgia State University. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
Peat, F. David (2002). From Certainty to Uncertainty: The Story of Science and Ideas in the Twenty-First Century. Joseph Henry Press
Reichenbach, Hans (1944). Philosophic Foundations of Quantum Mechanics. University of California Press. ISBN 0486404595. LCCN a440-4471
Schlipp, Paul Arthur (1949). Albert Einstein: Philosopher-Scientist. Tudor Publishing Company. LCCN 50-5340
Scientific American Reader, 1953.
Sears, Francis Weston (1949). Optics (3rd ed.). Addison-Wesley. ISBN 0195046013. LCCN 51-1018
Shimony, A. (1983). "(title not given in citation)". Foundations of Quantum Mechanics in the Light of New Technology (S. Kamefuchi et al., eds.). Tokyo: Japan Physical Society. p. 225.; cited in: Popescu, Sandu; Daniel Rohrlich (1996). "Action and Passion at a Distance: An Essay in Honor of Professor Abner Shimony". arXiv:quant-ph/9605004。
Tavel, Morton; Tavel, Judith (illustrations) (2002). Contemporary physics and the limits of knowledge. Rutgers University Press. ISBN 978-0813530772
Van Vleck, J. H.,1928, "The Correspondence Principle in the Statistical Interpretation of Quantum Mechanics", Proc. Natl. Acad. Sci. 14: 179.
Westmoreland; Benjamin Schumacher (1998). "Quantum Entanglement and the Nonexistence of Superluminal Signals". arXiv:quant-ph/9801014。
Wheeler, John Archibald; Feynman, Richard P. (1949). “Classical Electrodynamics in Terms of Direct Interparticle Action”. Reviews of Modern Physics 21 (3): 425–33. Bibcode: 1949RvMP...21..425W. doi:10.1103/RevModPhys.21.425.
Wieman, Carl; Perkins, Katherine (2005). “Transforming Physics Education”. Physics Today 58 (11): 36. Bibcode: 2005PhT....58k..36W. doi:10.1063/1.2155756.

外部リンク

"Microscopic World – Introduction to Quantum Mechanics". by Takada, Kenjiro, Emeritus professor at Kyushu University
Quantum Theory. at encyclopedia.com
The spooky quantum
The Quantum Exchange (tutorials and open-source learning software).
Atoms and the Periodic Table
Single and double slit interference
Time-Evolution of a Wavepacket in a Square Well An animated demonstration of a wave packet dispersion over time.
Experiments with single photons An introduction into quantum physics with interactive experiments
Carroll, Sean M.. “Quantum Mechanics (an embarrassment)”. Sixty Symbols. Brady Haran for the University of Nottingham. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
Comprehensive animations
"Quantum Mechanics and the Structure of Atoms" - YouTube The actual physics lesson begins 2:20 into the video.

{{DEFAULTSORT:りようしりきかくのかいろん}} [[Category:量子力学| ]]

[5] 熱放射の実験的測定のいくつかを記述できる数式がいくつか作られた。放射が最も強くなる波長が温度によりどのように変化するかはヴィーンの変位則により与えられ、単位面積当たりに放出される全体的なエネルギーはシュテファン＝ボルツマンの法則により与えられる。実験結果の最良の理論的説明はレイリー・ジーンズの法則であった。これは長波長（低周波数）では実験結果とよく一致するが、短波長（高周波数）ではほとんど一致しない。実際、短波長では、古典物理学はエネルギーが無限の速度で高温の物体から放出されると予測していた。明らかに間違っているこの結果は紫外破綻として知られている

[7] 量子(quantum)という言葉はラテン語で「どれくらい」("how much")を意味する言葉に由来する（量(quantity)も同様）。プランクの調和振動子のエネルギーとして量子化されたものは、特定の値しかとることができない。例えば、ほとんどの国でお金は効果的に量子化されており、「お金の量子」は流通している最も額面の低い硬貨である。力学は、物体に対する力の作用を扱う科学の分野である。したがって、量子力学は特定の特性が量子化されている物体を処理する力学の一分野である。

[15] 実際には、強度に依存する効果が存在する可能性があるが、非レーザー光源で実現可能な強度ではこれらの効果は観測することができない。

[18] アインシュタインの光電効果の方程式は「光子」の概念を必要せずに導出され、説明することができる。つまり、物質中の電子が量子力学の法則によって扱われる限り、電磁放射は古典的な電磁波として扱うことができる。結果は電子放出率とその角度分布の両方について、熱光源（太陽、白熱灯など）に対して定量的に正しいものである。この点の詳細については^[14]参照

[21] 原子の古典的なモデルは惑星モデル、またはラザフォードモデルと呼ばれる。この名は核の存在を最初に実証したガイガー＝マースデンの実験に基づいて1911年に提案したアーネスト・ラザフォードにちなむ。

[26] この場合、電子のエネルギーは、その運動エネルギーと位置エネルギーの和である。電子は原子核の周りの実際の運動により運動エネルギーを有し、原子核との電磁相互作用により位置エネルギーを有し。

[27] このモデルは原子核と単一の電子（つまり1つの電子のみを含むHe⁺ や O⁷⁺ などのイオン）で構成される任意の軽の放出スペクトルを考慮して簡単に変更できるが、中性のヘリウムなど2つの電子を有する原子に拡張することはできない。

[29] 電子回折はド・ブロイが仮説を発表してから3年後に初めて実証された。アバディーン大学で、ジョージ・パジェット・トムソンが電子線を金属薄膜に通し、ド・ブロイの仮説により予測されるような回折パターンを観測した。ベル研究所では、デイヴィソンとガーマーが結晶グリッドを通して電子線を導いた。ド・ブロイはその仮説により1929年にノーベル物理学賞を受賞した。トムソンとデイヴィソンは実験的研究によりノーベル物理学賞を共同受賞した。

[42] For a somewhat more sophisticated look at how Heisenberg transitioned from the old quantum theory and classical physics to the new quantum mechanics, see Heisenberg's entryway to matrix mechanics.

[1] “Quantum Mechanics”. National Public Radio. 22 June 2016閲覧。

[2] Kuhn, Thomas S. The Structure of Scientific Revolutions. Fourth ed. Chicago; London: The University of Chicago Press, 2012. Print.

[3] “Introduction to Quantum Mechanics”. Socratease. 2017年9月15日時点のオリジナルよりアーカイブ。 Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[4] Feynman, Richard P. (1988). QED : the strange theory of light and matter (1st Princeton pbk., seventh printing with corrections. ed.). Princeton, NJ: Princeton University Press. pp. 10. ISBN 978-0691024172

[6] This result was published (in German) as Planck, Max (1901). “Ueber das Gesetz der Energieverteilung im Normalspectrum”. Ann. Phys. 309 (3): 553–63. Bibcode: 1901AnP...309..553P. doi:10.1002/andp.19013090310. オリジナルの10 June 2012時点におけるアーカイブ。. . English translation: “On the Law of Distribution of Energy in the Normal Spectrum”. 18 April 2008時点のオリジナルよりアーカイブ。 Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[8] Francis Weston Sears (1958). Mechanics, Wave Motion, and Heat. Addison-Wesley. p. 537

[9] “The Nobel Prize in Physics 1918”. Nobel Foundation. 2009年8月1日閲覧。

[Kragh-10] Kragh, Helge (1 December 2000). “Max Planck: the reluctant revolutionary”. PhysicsWorld.com. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[11] Einstein, Albert (1905). “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt”. Annalen der Physik 17 (6): 132–48. Bibcode: 1905AnP...322..132E. doi:10.1002/andp.19053220607. , translated into English as On a Heuristic Viewpoint Concerning the Production and Transformation of Light Archived 11 June 2009 at the Wayback Machine.. The term "photon" was introduced in 1926.

[12] “Revival of the Wave Theory of Light in the Early Nineteenth-Century”. www.encyclopedia.com. 16 October 2018閲覧。

[taylor_127-9-13] Taylor, J. R.; Zafiratos, C. D.; Dubson, M. A. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. pp. 127–29. ISBN 0135897890

[Hawking-14] Hawking, Stephen (November 6, 2001) (英語). The Universe in a Nutshell. 55. Impey, C.D.. Bantam Spectra (April 2002発行). p. 80~. doi:10.1063/1.1480788. ISBN 978-0553802023. オリジナルのJuly 20, 2016時点におけるアーカイブ。 December 14, 2020閲覧。

[16] Dicke, Robert Henry; Wittke, James P. (1960). Introduction to Quantum Mechanics. Addison-Wesley Publishing Company. p. 12. ISBN 978-0201015102

[17] “The Photoelectric Effect Without Photons”. NTRS.NASA.gov. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[19] Jim Lucas: 'What Is Ultraviolet Light?', 15 September 2017, at livescience.com Accessed 27 December 2017

[20] 'Two Equations Governing Light's Behavior: Part Two E = hν' at chemteam.info Accessed 27 December 2017

[taylor_147-8-22] Taylor, J. R.; Zafiratos, C. D.; Dubson, M. A. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. pp. 147–48. ISBN 0135897890

[23] McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. pp. 70–89, [89]. ISBN 1840465778

[WorldBook-24] World Book.Inc (2007). “22” (英語). World Book Encyclopedia (Electronic reproduction). The World Book encyclopedia. 22 (3 ed.). Chicago, Illinois: World Book. p. 6. ISBN 978-0716601074. OCLC 894799866. オリジナルの2011時点におけるアーカイブ。 December 14, 2020閲覧。

[25] Wittke, J.P; Dicke, R.H (June 1, 1961). “11”. In Holladay, W.G. (英語). Introduction to Quantum Mechanics (eBook). 16. Nashville, Tennessee: ADDISON WESLEY LONGMAN INC. January 1, 1978. p. 10. ASIN B000K3HWYO. doi:10.1063/1.3057610. ISBN 978-0201015102. OCLC 53473 December 14, 2020閲覧。

[28] McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. pp. 110ff. ISBN 1840465778

[30] Aczel, Amir D., Entanglement, pp. 51ff. (Penguin, 2003) ISBN 978-1551926476

[31] McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. p. 114. ISBN 1840465778

[Zettili-32] Zettili, Nouredine (2009). Quantum Mechanics: Concepts and Applications. John Wiley and Sons. pp. 26–27. ISBN 978-0470026786

[Selleri-33] Selleri, Franco (2012). Wave-Particle Duality. Springer Science and Business Media. pp. 41. ISBN 978-1461533320

[Podgorsak-34] Podgorsak, Ervin B. (2013). Compendium to Radiation Physics for Medical Physicists. Springer Science and Business Media. pp. 88. ISBN 978-3642201868

[Halliday&Resnick-35] Halliday, David; Resnick, Robert (2013). Fundamentals of Physics, 10th Ed.. John Wiley and Sons. pp. 1272. ISBN 978-1118230619

[Myers-36] Myers, Rusty L. (2006). The Basics of Physics. Greenwood Publishing Group. pp. 172. ISBN 0313328579. "complementarity principle wave-particle duality."

[ShamosGreatExperiments-37] Shamos, Morris H (1 January 1987). Great Experiments in Physics: Firsthand Accounts from Galileo to Einstein. Courier Corporation. p. 108

[38] Merali, Zeeya (21 May 2015). “Quantum physics: What is really real?”. Nature: pp. 278–80. Bibcode: 2015Natur.521..278M. doi:10.1038/521278a 7 January 2017閲覧。

[39] Eibenberger, Sandra (2013). “Matter–wave interference of particles selected from a molecular library with masses exceeding 10 000 amu”. Physical Chemistry Chemical Physics 15 (35): 14696–700. arXiv:1310.8343. Bibcode: 2013PCCP...1514696E. doi:10.1039/C3CP51500A. PMID 23900710. "[I]n a three-grating interferometer... We observe high-contrast quantum fringe patterns of molecules... having 810 atoms in a single particle."

[40] McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. p. 87. ISBN 1840465778

[Heisenberg1925-41] Van der Waerden, B. L. (1967) (英語). Sources of Quantum Mechanics. Mineola, NY: Dover Publications. pp. 261–76. "Received 29 July 1925" See Werner Heisenberg's paper, "Quantum-Theoretical Re-interpretation of Kinematic and Mechanical Relations" pp. 261–76

[SchrBiog-43] Nobel Prize Organization. “Erwin Schrödinger – Biographical”. 28 March 2014閲覧。 “His great discovery, Schrödinger's wave equation, was made at the end of this epoch-during the first half of 1926.”

[EB-SchrEquation-44] "Schrodinger Equation (Physics)", Encyclopædia Britannica

[45] Erwin Schrödinger, "The Present Situation in Quantum Mechanics", p. 9. "This translation was originally published in Proceedings of the American Philosophical Society, 124, 323–38, and then appeared as Section I.11 of Part I of Quantum Theory and Measurement (J. A. Wheeler and W. H. Zurek, eds., Princeton University Press, NJ 1983). This paper can be downloaded here: Erwin Schrödinger. “A Translation of Schrödinger's "Cat Paradox Paper"”. 2010年11月13日時点のオリジナルよりアーカイブ。 Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[46] Heisenberg, W. (1955). The development of the interpretation of the quantum theory, pp. 12–29 in Niels Bohr and the Development of Physics: Essays dedicated to Niels Bohr on the occasion of his seventieth birthday, edited by Pauli, W. with the assistance of Rosenfeld, L. and Weisskopf, V., Pergamon, London, p. 13: "the single quantum jump ... is "factual" in nature".

[47] W. Moore, Schrödinger: Life and Thought, Cambridge University Press (1989), p. 222. See p. 227 for Schrödinger's own words.

[nytimesQuantumJump-48] “Physicists finally get to see quantum jump with own eyes”. The New York Times. 30 November 2019閲覧。

[49] “The Nobel Prize in Physics 1932”. NobelPrize.org. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[50] Heisenberg first published his work on the uncertainty principle in the leading German physics journal Zeitschrift für Physik: Heisenberg, W. (1927). “Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik”. Z. Phys. 43 (3–4): 172–98. Bibcode: 1927ZPhy...43..172H. doi:10.1007/BF01397280.

[51] “The Nobel Prize in Physics 1932”. NobelPrize.org. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[EB-uncertainty-52] "Uncertainty principle", Encyclopædia Britannica

[Pauling-53] Pauling, Linus (1960). The Nature of the Chemical Bond (3rd ed.). Itahca, NY: Cornell University Press. p. 47. ISBN 0801403332 1 March 2016閲覧。

[EB-orbital-54] "Orbital (chemistry and physics)", Encyclopædia Britannica

[55] E. Schrödinger, Proceedings of the Cambridge Philosophical Society, 31 (1935), p. 555, says: "When two systems, of which we know the states by their respective representation, enter into a temporary physical interaction due to known forces between them and when after a time of mutual influence the systems separate again, then they can no longer be described as before, viz., by endowing each of them with a representative of its own. I would not call that one but rather the characteristic trait of quantum mechanics."

[56] David Kaiser, Is Quantum Entanglement Real?, The New York Times, Nov. 2014.

[57] John G. Cramer. “Quantum Nonlocality and the Possibility of Superluminal Effects”. npl.washington.edu. 29 December 2010時点のオリジナルよりアーカイブ。 Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[58] "Mechanics", Merriam-Webster Online Dictionary

[EB-field-59] "Field", Encyclopædia Britannica

[Hammond-60] Richard Hammond, The Unknown Universe, New Page Books, 2008. ISBN 978-1601630032

[61] “Featured Physicists – Paul Dirac 1902–1984”. www.physicalworld.org. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[nobel-62] “The Nobel Prize in Physics 1933”. Nobel Foundation. 2007年11月24日閲覧。

[63] “Exchange Particles”. hyperphysics.phy-astr.gsu.edu. 16 October 2018閲覧。

[64] “Ten years of Large Hadron Collider discoveries below Swiss countryside are just the start of decoding the universe”. www.thelocal.ch (5 October 2018). 16 October 2018閲覧。

[65] “Copenhagen Interpretation”. abyss.uoregon.edu. 16 October 2018閲覧。

[66] Durrani, Z. A. K.; Ahmed, H. (2008). Vijay Kumar. ed. Nanosilicon. Elsevier. p. 345. ISBN 978-0080445281

[1]

[2]

[3]

[4]

[note 1]

[5]

[note 2]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[note 3]

[13]

[note 4]

[15]

[16]

[note 5]

[17]

[18]

[19]

[20]

[note 6]

[note 7]

[21]

[note 8]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[note 9]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[14]

表話編歴量子力学
全般	序論（英語版）数学的定式化
背景	古典力学前期量子論量子論量子力学の歴史量子力学の年表
基本概念	量子状態波動関数重ね合わせ不確定性原理可観測量相補性二重性不確定性トンネル効果排他原理エーレンフェストの定理量子もつれデコヒーレンス
定式化	シュレーディンガー描像ハイゼンベルク描像相互作用描像波動力学行列力学経路積分 GNS表現
方程式	シュレーディンガー方程式ハイゼンベルク方程式パウリ方程式クライン＝ゴルドン方程式ディラック方程式
実験	二重スリット実験シュテルン＝ゲルラッハの実験デイヴィソン＝ガーマーの実験ベルの不等式の検証実験（英語版）ポパーの実験（英語版）シュレーディンガーの猫爆弾検査問題（英語版）量子消しゴム実験
解釈（英語版）	観測問題ボーム解釈無矛盾歴史コペンハーゲン解釈アンサンブル解釈隠れた変数理論多世界解釈客観的収縮（英語版）量子論理関係性量子力学 (RQM)（英語版）確率過程量子化交流解釈（英語版）フォン・ノイマン＝ウィグナー解釈
人物	ジョン・スチュワート・ベルデヴィッド・ボームニールス・ボーアマックス・ボルンサティエンドラ・ボースルイ・ド・ブロイポール・ディラックポール・エーレンフェストヒュー・エヴェレット3世リチャード・P・ファインマンヴェルナー・ハイゼンベルクパスクアル・ヨルダンヘンリク・アンソニー・クラマースジョン・フォン・ノイマンヴォルフガング・パウリマックス・プランクエルヴィン・シュレーディンガーアルノルト・ゾンマーフェルトヴィルヘルム・ヴィーンユージン・ウィグナー
関連項目	散乱理論相対論的量子力学場の量子論量子情報量子カオス量子コンピューター
カテゴリ