コンテンツにスキップ

英文维基 | 中文维基 | 日文维基 | 草榴社区

TLA+

出典: フリー百科事典『ウィキペディア（Wikipedia）』
TLA+
パラダイム Action
登場時期

1999年4月23日 (25年前) (1999-04-23)

[1]
設計者 Leslie Lamport
最新リリース TLA+2/ 2014年1月15日 (10年前) (2014-01-15)[2]
プラットフォーム Cross-platform (multi-platform)
ライセンス MIT License[3]
ウェブサイト research.microsoft.com/en-us/um/people/lamport/tla/tla.html
拡張子 .tla
テンプレートを表示

TLA+は、Leslie Lamportによって開発された形式仕様言語。並行システムと分散システムの設計、モデル化、文書化、および検証に使用される。 TLA+は、網羅的にテスト可能な擬似コード[4]として説明されており、その使用はソフトウェアシステムの設計図を描くことに喩えられる。 [5] TLAはTemporal Logic of Actionsの頭字語である。

設計と文書化に関して、TLA+ は非公式の技術仕様と同じ目的を果たす。ただし、TLA+の仕様は論理学と数学の形式言語で記述されており、この言語で記述された仕様の精度は、システムの実装が始まる前に設計上の欠陥を明らかにすることを目的としている。 [6]

TLA+のコードは形式言語で記述するため、有限モデル検査に適する。モデルチェッカーは、いくつかの実行ステップまでのすべての可能なシステム動作を見つけ、安全性や活性などの望ましい不変性プロパティの違反を調べる。 TLA+のコードでは、基本的な集合論を使用して安全性（悪いことが起こらない事）を定義し、時相論理を使用して活性（良いことがいずれ起こる事）を定義する。

TLA+は、アルゴリズムと数学的定理の両方について、マシンでチェックされた正確性の証明を作成するためにも使用される。証明は、単一の定理証明者バックエンドに依存しない宣言型の階層スタイルで記述される。公式および非公式の構造化された数学的証明は、TLA+で記述できる。言語はLaTeXに似ており、TLA+のコードをLaTeXドキュメントに翻訳するためのツールが存在する。 [7]

TLA+は、並行システムの検証方法に関する数十年の研究の後、1999年に公開された。その後、IDEや分散モデルチェッカーなどのツールチェーンが開発された。擬似コードのような言語PlusCalは2009年に作成され、TLA+にトランスパイルされ、シーケンシャルアルゴリズムを記述する際に有用とされる。 TLA+2は2014年に発表され、プルーフコンストラクトの言語サポートを拡張した。現在のTLA+リファレンスは、LeslieLamportによるTLA+Hyperbookである。

歴史

[編集]
Portrait of an Israeli man in his sixties. His hair is short and balding, and he is wearing glasses with a dress shirt and jacket.
アミール・プヌーリは、コンピュータサイエンスに時相論理を適用し、1996年のチューリング賞を受賞した。

現代の時相論理は、1957年にアーサー・プライアーによって開発され、当時は時制論理と呼ばれていた。アミール・プヌーリが、コンピュータサイエンスへの時相論理の適用を真剣に研究した最初の人物だったが、アーサー・プライアーは1967年の10年前に既にその使用について予測していた。

プヌーリは、コンピュータープログラムの指定と推論における時相論理の使用を研究し、1977年に線形時相論理を導入した。 線形時相論理は、排他制御やデッドロックの解決などの特性を簡単に表現する、並行プログラムの分析のための重要なツールとなった。 [8]

プヌーリの線形時相論理に関する研究と同時に、学者はマルチプロセスプログラムの検証のためにホーア論理を一般化するために取り組んでいた。レスリー・ランポートは、ピアレビューで相互排除について提出した論文に誤りが見つかった後、この問題に関心を持つようになった。 Ed Ashcroftは、1975年の論文「Proving Assertions About Parallel Programs」で不変性を紹介した。これは、Lamportが1977年の論文「Proving Correctness of Multiprocess Programs」でFloydの方法を一般化するために使用した。ランポートの論文はまた、部分正当性と終了の一般化として、それぞれ安全性と活性を紹介した。 [9]この方法は、EdsgerDijkstraによる1978年の論文で最初の同時ガベージコレクションアルゴリズムを検証するために使用された。 [10]

ランポートは、スーザンオウィッキが主催したスタンフォードでの1978年のセミナーで、プヌーリのLTLに最初に遭遇しました。ランポートによると「時相論理は、実用化されそうもなく抽象的で無意味だと確信していたが、楽しそうだったので参加した。」 との事であったが、1980年に彼は「'Sometime' is Sometimes 'Not Never'」を出版し、時相論理の文献で最も頻繁に引用される論文の1つとなった。 [11] ランポートは、SRI在籍中に時相論理仕様の作成に取り組んだが、このアプローチは実用的ではないとわかった。

Portrait of a Caucasian man in his seventies with medium-length gray hair and a full gray beard, wearing glasses and a T-shirt.
TLA+ は、コンピューター科学者であり、2013年チューリング賞を受賞したレスリーランポートによって開発された。

彼が実用的な仕様方法を模索した結果として1983年に論文「Specifying Concurrent Programming Modules」が生まれた。この論文では、状態遷移をプライム変数と非プライム変数のブール値関数として記述するというアイデアが導入されている。 [12]その模索は1980年代に継続され、ランポートは1990年にアクションの時相論理に関する論文群の発表を開始した。しかし、1994年に「アクションの時相論理」が発表されるまでは正式には導入されなかった。 TLAは、時間式でのアクションの使用を可能にした。これは、ランポートによれば、「並行システム検証で使用されるすべての推論を形式化および体系化するための洗練された方法を提供する。」とされている。[13]

TLAの仕様は、ほとんどが通常の非時相論的数学で構成されていたが、Lamportは、純粋な時間的仕様よりも煩わしさが少ないと発見した。 TLAは、1999年に論文「Specifying Concurrent Systems with TLA+」で紹介され、TLA+の仕様記述言語としての数学的基礎を提供した。同じ年の後半に、YuanYuはTLA+仕様のTLCモデルチェッカーを作成した。 TLCは、Compaqマルチプロセッサのキャッシュコヒーレンスプロトコルのエラーを見つけるために使用された。[14]

ランポートは、2002年に「Specifying Systems：TLA+ Language and Tools for Software Engineers」というタイトルの+に関する完全な教科書を発行した。 [15] PlusCalは2009年に導入され[16] 、TLA+プルーフシステム（TLAPS）は2012年[17]、 TLA+2は2014年に発表され、いくつかの言語構造が追加され、プルーフシステムの言語内サポートが大幅に増加した。 ランポートは、更新されたTLA+のリファレンスである「The TLA+ Hyperbook」の作成に取り組んでいる。未完成な作品は彼の公式ウェブサイトから入手できる。Lamportは、TLA+ビデオコースも作成している。このコースでは、「プログラマーとソフトウェアエンジニアにTLA+コードの記述方法を教える入門から始まる一連のビデオレクチャーを作りかけている」と説明されている。

言語

[編集]

TLA+コードは複数のモジュールからなる。モジュールは、他のモジュールを拡張（インポート）して、その機能を使用できる。 TLA+標準はタイプセット数学記号で指定されているが、既存のTLA+ツールは、ASCIIでLaTeXのような記号定義を使用する。 TLA+では、定義が必要ないくつかの用語を使用する。

  • State – 変数への値の代入
  • Behaviour – 連続したState
  • Step – Behaviourでの連続したStateのペア
  • Shuttering step – 変数が変更されないStep
  • Next-state relation – 変数が任意のStepでどのように変化するかを説明する関係
  • State function – Next-state relationではない変数と定数を含む式
  • State predicate – ブール値の状態関数
  • Invariant – 到達可能なすべてのStateで真とする状態述語
  • Temporal formula – 時相論理のステートメントを含む式

安全性

[編集]

TLA+は、すべての正しいシステム動作のBehaviorを定義することを目的としている。例えば、0と1の間で際限なく刻々と変化する1ビットクロックは、次のように記述できる。

VARIABLE clock

Init == clock \in {0, 1}

Tick == IF clock = 0 THEN clock' = 1 ELSE clock' = 0

Spec == Init /\ [][Tick]_<<clock>>

Relation Tickはクロックが1であればclock'（次のStateにおけるclockの値）は0、0であれば1を設定する。clockの値が0または1の場合、State PredicateであるInitはtrueである。 Specは、1ビットクロックのすべてのBehaviorが最初にInitを満たし、すべてのStepがTickに一致するか、Shuttering stepである必要があることをアサートするTemporal formulaである。そのような2つの動作は次の通りである。

0 -> 1 -> 0 -> 1 -> 0 -> ...

1 -> 0 -> 1 -> 0 -> 1 -> ...

1ビットクロックの安全性は –到達可能なシステム状態の集合 –という仕様によって適切に説明される。

活性

[編集]

上記の仕様では、1ビットクロックの奇妙な状態は許可されていないが、クロックが常に変化するとは言っていない。たとえば、次のような永続的なShuttering stepが起こりうる。

0 -> 0 -> 0 -> 0 -> 0 -> ...

1 -> 1 -> 1 -> 1 -> 1 -> ...

変化しない時計は役に立たないので、これらの振る舞いは禁止されるべきである。 1つの解決策はShuttering stepを無効にする事であるが、TLA+では常にShutteringを有効にする必要がある。Shuttering stepは、仕様に記載されていないシステムの一部への変更を表し、改良に有用である。最終的にTickしなければならないクロックを確保するために、弱い公平性がTickのためにアサートできる。

Spec == Init /\ [][Tick]_<<clock>> /\ WF_<<clock>>(Tick)

アクションに対する公平性が弱いということは、そのアクションが継続的に有効になっている場合は、最終的に実行する必要があることを意味する。Tickの公平性が弱いため、ティック間で許可されるShuttering stepの数は限られている。 Tickに関するこの時相論理ステートメントは、活性アサーションと呼ばれる。一般に、活性アサーションはマシンで閉じる必要がある。到達可能な状態のセットを制約するのではなく、可能な動作のセットのみを制約する必要がある。 [18]

ほとんどの仕様では、活性の表明は必要ない。安全性特性だけでモデル検査とシステム実装の両方に対して事足りる。 [19]

演算子

[編集]

TLA+はZFに基づいているため、変数の操作にはセット操作が含まれる。言語には、集合元、和集合、共通部分集合、差集合、べき集合、および部分集合演算子が含まれる。 ∨ 、 ∧ 、 ¬ 、 ⇒ 、 ↔ 、 ≡などの一階述語論理演算子、および全称記号および存在記号∀と∃も含まれている。ヒルベルトのεは、任意の集合要素を一意に選択するCHOOSE演算子として提供される。実数、整数、自然数の算術演算子は、標準モジュールから利用可能である。

時相論理演算子はTLA+に組み込まれている。時間式では を"Pが常に真である"を意味し、 を "Pが最終的に真となる"を意味するという使い方をする。演算子は結合されは"Pが無限に頻繁に真である"を意味する、またはは、"最終的にPは常に真になる"という意味となる。他の時相演算子には、弱い公平性と強い公平性が含まれる。弱い公平を表すWFe（A）は、アクションAが連続して（つまり絶え間なく）有効になっている場合、それが最終的に実施される事を意味する。強い公平を表すSFe(A)アクションAは、（中断の有無にかかわらず、繰り返し）継続的に有効になっている場合は、それが最終的に実施される事を意味する。

ツールからのサポートはないが時相論的な存在記号と全称記号はTLA+に含まれている。

ユーザー定義の演算子はマクロに似ている。演算子は、ドメインが集合である必要がないという点において関数とは異なる。たとえば、集合のメンバーシップ演算子は、そのドメインとして集合の圏を持つが、これはZFCでは有効な集合ではない（その存在はラッセルのパラドックスにつながるため）。再帰的で匿名のユーザー定義演算子がTLA+2に追加された。

データ構造

[編集]

TLA+の基本的なデータ構造とは集合である。集合は、明示的に列挙されるか、演算子を使用するか、 {x \in S : p} （pはxの条件）または{e : x \in S} （eはxの関数）を使用して他の集合から構築される。一意の空集合は{}として表される。

TLA+の関数は、ドメイン内の各要素集合に値を割り当てる。 [S -> T]は、定義域集合Sの各xについて、Tにf [x]を持つすべての関数の集合である。例えばTLA+関数Double[x \in Nat] == x*2 とは集合 [Nat -> Nat]の一要素であるため、 Double \in [Nat -> Nat]はTLA+の真のステートメントである。関数は、一部の式e [x \in S |-> e]を使用するか、既存の関数を変更することによっても定義される[f EXCEPT ![v 1 ] = v 2 ] 。

レコードはTLA+の関数の一種である。レコード[name |-> "John", age |-> 35]は、フィールドnameとageを持つレコードであり、 r.nameやr.ageでアクセスされ、レコードの集合[name : String, age : Nat]に所属する。

タプルはTLA+に含まれている。 <<e 1 ,e 2 ,e 3 >>は明示的に定義されるか、標準のシーケンスモジュールの演算子で構成される。タプルの集合は、デカルト積によって定義される。たとえば、自然数のすべてのペアの集合は、 Nat \X Natとして定義される。

標準モジュール

[編集]

TLA+には、一般的な演算子を含む一連の標準モジュールがある。それらは構文アナライザーで配布される。 TLCモデルチェッカーは、パフォーマンスを向上させるためにJava実装を使用する。

  • FiniteSets ：有限集合を扱うためのモジュール。 IsFiniteSet（S）およびCardinality（S）演算子を提供する。
  • Sequences： Len（S）、Head（S）、Tail（S）、Append（S、E） 、連結、フィルターなどのタプルの演算子を定義する。
  • Bags： 多重集合を扱うためのモジュール。プリミティブな集合演算の類似物と重複カウントを提供する。
  • Naturals： 不等式および算術演算子とともに自然数を定義する。
  • Integers：整数を定義する。
  • Reals：実数と除算と無限大を定義する。
  • RealTime：リアルタイムのシステム仕様で役立つ定義を提供する。
  • TLC ：ロギングやアサーションなど、モデルでチェックされた仕様のユーティリティ関数を提供する。

標準モジュールはEXTENDSまたはINSTANCEステートメントでインポートされる。

ツール

[編集]

IDE

[編集]
TLA+ Toolbox
TLA+ IDE in typical use showing spec explorer on the left, editor in the middle, and parse errors on the right.
作者 Simon Zambrovski, Markus Kuppe, Daniel Ricketts
開発元 Hewlett-Packard, Microsoft
初版 2010年2月4日 (14年前) (2010-02-04)
最新版
1.7.0 / 2020年4月25日 (4年前) (2020-04-25)
最新評価版
1.7.1 / 2020年5月1日 (4年前) (2020-05-01)
リポジトリ github.com/tlaplus/tlaplus
プログラミング
言語		 Java
種別 Integrated development environment
ライセンス MIT License
公式サイト research.microsoft.com/en-us/um/people/lamport/tla/toolbox.html
テンプレートを表示

統合開発環境はEclipseの上に実装されている。これには、エラーとシンタックスハイライトを備えたエディターに加えて、他のいくつかのTLA+ツールへのGUIフロントエンドが含まれる。

  • SANY構文アナライザー。仕様を解析して構文エラーをチェックする。
  • pretty-printされた仕様を生成するためのLaTeXトランスレータ。
  • PlusCalトランスレータ。
  • TLCモデルチェッカー。
  • TLAPSプルーフシステム。

IDEはTLAツールボックスで配布される。

モデルチェッカー

[編集]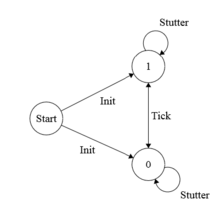
Finite state machine diagram of one-bit clock
1ビットクロックに対してTLCによって検出された状態と遷移。

TLCモデルチェッカーは、不変性プロパティをチェックするためのTLA+コードの有限状態モデルを構築する。 TLCは、仕様を満たす初期状態のセットを生成し、定義されたすべての状態遷移に対して幅優先探索を実行する。すべての状態遷移がすでに検出された状態につながると、実行は停止する。 TLCがシステム不変条件に違反する状態を検出すると、TLCは停止し、問題のある状態への状態トレースパスを提供する。 TLCは、組み合わせ爆発を防ぐためにモデルの対称性を宣言する方法を提供する。[14]また並列計算状態探索ステップを並列化し、分散モードで実行して、ワークロードを多数のコンピューターに分散させる事もできる。[20]

徹底的な幅優先探索の代わりに、TLCは深さ優先探索を使用するか、ランダムな動作を生成できる。 TLCはTLA+のサブセットで動作する。モデルは有限で列挙可能でなければならず、一部の時相演算子はサポートされていない。分散モードでは、TLCは活性特性をチェックすることも、ランダムまたは深さ優先の動作をチェックすることもできない。 TLCは、コマンドラインツールとして、またはTLAツールボックスにバンドルされて利用できる。

TLA+プルーフシステム（TLAPS）は、TLA+で記述されたプルーフを機械的にチェックする。これは、Microsoft Research - INRIA Joint Centerで開発され、並行アルゴリズムと分散アルゴリズムの正確性を証明する。証明言語は、特定の定理証明者から独立するように設計されており、証明は宣言型で記述され、複数の個別の義務として変換されバックエンドの証明者に送信される。主なバックエンドの証明者はIsabelleとZenonであり、 SMTソルバーCVC3 、 Yices 、およびZ3定理証明者にフォールバックする。 TLAPSプルーフは階層構造になっているため、リファクタリングが容易になり、非線形開発が可能となる。前のすべてのステップが検証される前に、後のステップで作業を開始でき、難しいステップはより小さなサブステップに分解される。モデルチェッカーは検証が開始される前に小さなエラーをすばやく見つけるため、TLAPSはTLCとうまく連携する。同様にしてTLAPSは、有限モデル検査の機能を超えるシステムプロパティを証明できる。 [17]

TLAPSは現在、実数による推論も、ほとんどの時間演算子もサポートしない。 IsabelleとZenonは通常、算術証明の義務を証明できないため、SMTソルバーを使用する必要がある。 [21] TLAPSは、ビザンチンPaxos 、Memoirセキュリティアーキテクチャ、およびPastry分散ハッシュテーブルのコンポーネントの正当性を証明するために使用されている。[17] これは他のTLA+ツールとは別に配布され、BSDライセンスの下で配布されるフリーソフトウェアである。 [22] TLA+2は、プルーフコンストラクトの言語サポートを大幅に拡張した。

業界での使用

[編集]

Microsoftでは、TLA+で仕様を作成する過程で、 Xbox 360メモリモジュールに重大なバグを発見した。 [23] TLA+は、ビザンチンPaxosおよびPastry分散ハッシュテーブルのコンポーネントの正式な証明を作成するために使用された。 [17]

アマゾンウェブサービスは2011年からTLA+を使用している。TLA+モデル検査によってDynamoDB 、 S3 、 EBS、および内部分散ロックマネージャーでバグを発見。一部のバグには、35ステップの状態トレースが必要であった。モデル検査は、積極的な最適化を検証するためにも使用された。さらに、TLA+仕様は、文書化および設計支援としての価値があることを確認した。 [4]

MicrosoftのAzureは、TLA+を使用して5つの異なる一貫性モデルをもち世界規模に分散したデータベースであるCosmos DBを設計した。 [24] [25]

例

[編集]
A key-value store with snapshot isolation
--------------------------- MODULE KeyValueStore ---------------------------
CONSTANTS   Key,            \* The set of all keys.
            Val,            \* The set of all values.
            TxId            \* The set of all transaction IDs.
VARIABLES   store,          \* A data store mapping keys to values.
            tx,             \* The set of open snapshot transactions.
            snapshotStore,  \* Snapshots of the store for each transaction.
            written,        \* A log of writes performed within each transaction.
            missed          \* The set of writes invisible to each transaction.
----------------------------------------------------------------------------
NoVal ==    \* Choose something to represent the absence of a value.
    CHOOSE v : v \notin Val

Store ==    \* The set of all key-value stores.
    [Key -> Val \cup {NoVal}]

Init == \* The initial predicate.
    /\ store = [k \in Key |-> NoVal]        \* All store values are initially NoVal.
    /\ tx = {}                              \* The set of open transactions is initially empty.
    /\ snapshotStore =                      \* All snapshotStore values are initially NoVal.
        [t \in TxId |-> [k \in Key |-> NoVal]]
    /\ written = [t \in TxId |-> {}]        \* All write logs are initially empty.
    /\ missed = [t \in TxId |-> {}]         \* All missed writes are initially empty.
    
TypeInvariant ==    \* The type invariant.
    /\ store \in Store
    /\ tx \subseteq TxId
    /\ snapshotStore \in [TxId -> Store]
    /\ written \in [TxId -> SUBSET Key]
    /\ missed \in [TxId -> SUBSET Key]
    
TxLifecycle ==
    /\ \A t \in tx :    \* If store != snapshot & we haven't written it, we must have missed a write.
        \A k \in Key : (store[k] /= snapshotStore[t][k] /\ k \notin written[t]) => k \in missed[t]
    /\ \A t \in TxId \ tx : \* Checks transactions are cleaned up after disposal.
        /\ \A k \in Key : snapshotStore[t][k] = NoVal
        /\ written[t] = {}
        /\ missed[t] = {}

OpenTx(t) ==    \* Open a new transaction.
    /\ t \notin tx
    /\ tx' = tx \cup {t}
    /\ snapshotStore' = [snapshotStore EXCEPT ![t] = store]
    /\ UNCHANGED <<written, missed, store>>

Add(t, k, v) == \* Using transaction t, add value v to the store under key k.
    /\ t \in tx
    /\ snapshotStore[t][k] = NoVal
    /\ snapshotStore' = [snapshotStore EXCEPT ![t][k] = v]
    /\ written' = [written EXCEPT ![t] = @ \cup {k}]
    /\ UNCHANGED <<tx, missed, store>>
    
Update(t, k, v) ==  \* Using transaction t, update the value associated with key k to v.
    /\ t \in tx
    /\ snapshotStore[t][k] \notin {NoVal, v}
    /\ snapshotStore' = [snapshotStore EXCEPT ![t][k] = v]
    /\ written' = [written EXCEPT ![t] = @ \cup {k}]
    /\ UNCHANGED <<tx, missed, store>>
    
Remove(t, k) == \* Using transaction t, remove key k from the store.
    /\ t \in tx
    /\ snapshotStore[t][k] /= NoVal
    /\ snapshotStore' = [snapshotStore EXCEPT ![t][k] = NoVal]
    /\ written' = [written EXCEPT ![t] = @ \cup {k}]
    /\ UNCHANGED <<tx, missed, store>>
    
RollbackTx(t) ==    \* Close the transaction without merging writes into store.
    /\ t \in tx
    /\ tx' = tx \ {t}
    /\ snapshotStore' = [snapshotStore EXCEPT ![t] = [k \in Key |-> NoVal]]
    /\ written' = [written EXCEPT ![t] = {}]
    /\ missed' = [missed EXCEPT ![t] = {}]
    /\ UNCHANGED store

CloseTx(t) ==   \* Close transaction t, merging writes into store.
    /\ t \in tx
    /\ missed[t] \cap written[t] = {}   \* Detection of write-write conflicts.
    /\ store' =                         \* Merge snapshotStore writes into store.
        [k \in Key |-> IF k \in written[t] THEN snapshotStore[t][k] ELSE store[k]]
    /\ tx' = tx \ {t}
    /\ missed' =    \* Update the missed writes for other open transactions.
        [otherTx \in TxId |-> IF otherTx \in tx' THEN missed[otherTx] \cup written[t] ELSE {}]
    /\ snapshotStore' = [snapshotStore EXCEPT ![t] = [k \in Key |-> NoVal]]
    /\ written' = [written EXCEPT ![t] = {}]

Next == \* The next-state relation.
    \/ \E t \in TxId : OpenTx(t)
    \/ \E t \in tx : \E k \in Key : \E v \in Val : Add(t, k, v)
    \/ \E t \in tx : \E k \in Key : \E v \in Val : Update(t, k, v)
    \/ \E t \in tx : \E k \in Key : Remove(t, k)
    \/ \E t \in tx : RollbackTx(t)
    \/ \E t \in tx : CloseTx(t)
        
Spec == \* Initialize state with Init and transition with Next.
    Init /\ [][Next]_<<store, tx, snapshotStore, written, missed>>
----------------------------------------------------------------------------
THEOREM Spec => [](TypeInvariant /\ TxLifecycle)
=============================================================================
ルールベースのファイアウォール
------------------------------ MODULE Firewall ------------------------------
EXTENDS   Integers
CONSTANTS  Address,  \* The set of all addresses
      Port,    \* The set of all ports
      Protocol  \* The set of all protocols

AddressRange == \* The set of all address ranges
  {r \in Address \X Address : r[1] <= r[2]}

InAddressRange[r \in AddressRange, a \in Address] ==
  /\ r[1] <= a
  /\ a <= r[2]

PortRange ==  \* The set of all port ranges
  {r \in Port \X Port : r[1] <= r[2]}

InPortRange[r \in PortRange, p \in Port] ==
  /\ r[1] <= p
  /\ p <= r[2]

Packet ==  \* The set of all packets
  [sourceAddress : Address,
  sourcePort : Port,
  destAddress : Address,
  destPort : Port,
  protocol : Protocol]

Firewall == \* The set of all firewalls
  [Packet -> BOOLEAN]

Rule == \* The set of all firewall rules
  [remoteAddress : AddressRange,
  remotePort : PortRange,
  localAddress : AddressRange,
  localPort : PortRange,
  protocol : SUBSET Protocol,
  allow : BOOLEAN]

Ruleset == \* The set of all firewall rulesets
  SUBSET Rule

Allowed[rset \in Ruleset, p \in Packet] == \* Whether the ruleset allows the packet
  LET matches == {rule \in rset :
    /\ InAddressRange[rule.remoteAddress, p.sourceAddress]
    /\ InPortRange[rule.remotePort, p.sourcePort]
    /\ InAddressRange[rule.localAddress, p.destAddress]
    /\ InPortRange[rule.localPort, p.destPort]
    /\ p.protocol \in rule.protocol}
  IN /\ matches /= {}
    /\ \A rule \in matches : rule.allow
=============================================================================
A multi-car elevator system
------------------------------ MODULE Elevator ------------------------------
(***************************************************************************)
(* This spec describes a simple multi-car elevator system. The actions in  *)
(* this spec are unsurprising and common to all such systems except for    *)
(* DispatchElevator, which contains the logic to determine which elevator  *)
(* ought to service which call. The algorithm used is very simple and does *)
(* not optimize for global throughput or average wait time. The            *)
(* TemporalInvariant definition ensures this specification provides        *)
(* capabilities expected of any elevator system, such as people eventually *)
(* reaching their destination floor.                                       *)
(***************************************************************************)

EXTENDS     Integers

CONSTANTS   Person,     \* The set of all people using the elevator system
            Elevator,   \* The set of all elevators
            FloorCount  \* The number of floors serviced by the elevator system

VARIABLES   PersonState,            \* The state of each person
            ActiveElevatorCalls,    \* The set of all active elevator calls
            ElevatorState           \* The state of each elevator

Vars == \* Tuple of all specification variables
    <<PersonState, ActiveElevatorCalls, ElevatorState>>

Floor ==    \* The set of all floors
    1 .. FloorCount

Direction ==    \* Directions available to this elevator system
    {"Up", "Down"}

ElevatorCall == \* The set of all elevator calls
    [floor : Floor, direction : Direction]

ElevatorDirectionState ==   \* Elevator movement state; it is either moving in a direction or stationary
    Direction \cup {"Stationary"}

GetDistance[f1, f2 \in Floor] ==    \* The distance between two floors
    IF f1 > f2 THEN f1 - f2 ELSE f2 - f1
    
GetDirection[current, destination \in Floor] == \* Direction of travel required to move between current and destination floors
    IF destination > current THEN "Up" ELSE "Down"

CanServiceCall[e \in Elevator, c \in ElevatorCall] ==   \* Whether elevator is in position to immediately service call
    LET eState == ElevatorState[e] IN
    /\ c.floor = eState.floor
    /\ c.direction = eState.direction

PeopleWaiting[f \in Floor, d \in Direction] ==  \* The set of all people waiting on an elevator call
    {p \in Person :
        /\ PersonState[p].location = f
        /\ PersonState[p].waiting
        /\ GetDirection[PersonState[p].location, PersonState[p].destination] = d}

TypeInvariant ==    \* Statements about the variables which we expect to hold in every system state
    /\ PersonState \in [Person -> [location : Floor \cup Elevator, destination : Floor, waiting : BOOLEAN]]
    /\ ActiveElevatorCalls \subseteq ElevatorCall
    /\ ElevatorState \in [Elevator -> [floor : Floor, direction : ElevatorDirectionState, doorsOpen : BOOLEAN, buttonsPressed : SUBSET Floor]]

SafetyInvariant ==   \* Some more comprehensive checks beyond the type invariant
    /\ \A e \in Elevator :  \* An elevator has a floor button pressed only if a person in that elevator is going to that floor
        /\ \A f \in ElevatorState[e].buttonsPressed :
            /\ \E p \in Person :
                /\ PersonState[p].location = e
                /\ PersonState[p].destination = f
    /\ \A p \in Person :    \* A person is in an elevator only if the elevator is moving toward their destination floor
        /\ \A e \in Elevator :
            /\ (PersonState[p].location = e /\ ElevatorState[e].floor /= PersonState[p].destination) => 
                /\ ElevatorState[e].direction = GetDirection[ElevatorState[e].floor, PersonState[p].destination]
    /\ \A c \in ActiveElevatorCalls : PeopleWaiting[c.floor, c.direction] /= {} \* No ghost calls

TemporalInvariant ==  \* Expectations about elevator system capabilities
    /\ \A c \in ElevatorCall :  \* Every call is eventually serviced by an elevator
        /\ c \in ActiveElevatorCalls ~> \E e \in Elevator : CanServiceCall[e, c]
    /\ \A p \in Person :    \* If a person waits for their elevator, they'll eventually arrive at their floor
        /\ PersonState[p].waiting ~> PersonState[p].location = PersonState[p].destination

PickNewDestination(p) ==    \* Person decides they need to go to a different floor
    LET pState == PersonState[p] IN
    /\ ~pState.waiting
    /\ pState.location \in Floor
    /\ \E f \in Floor :
        /\ f /= pState.location
        /\ PersonState' = [PersonState EXCEPT ![p] = [@ EXCEPT !.destination = f]]
    /\ UNCHANGED <<ActiveElevatorCalls, ElevatorState>>

CallElevator(p) ==  \* Person calls the elevator to go in a certain direction from their floor
    LET pState == PersonState[p] IN
    LET call == [floor |-> pState.location, direction |-> GetDirection[pState.location, pState.destination]] IN
    /\ ~pState.waiting
    /\ pState.location /= pState.destination
    /\ ActiveElevatorCalls' =
        IF \E e \in Elevator :
            /\ CanServiceCall[e, call]
            /\ ElevatorState[e].doorsOpen
        THEN ActiveElevatorCalls
        ELSE ActiveElevatorCalls \cup {call}
    /\ PersonState' = [PersonState EXCEPT ![p] = [@ EXCEPT !.waiting = TRUE]]
    /\ UNCHANGED <<ElevatorState>>

OpenElevatorDoors(e) == \* Open the elevator doors if there is a call on this floor or the button for this floor was pressed.
    LET eState == ElevatorState[e] IN
    /\ ~eState.doorsOpen
    /\  \/ \E call \in ActiveElevatorCalls : CanServiceCall[e, call]
        \/ eState.floor \in eState.buttonsPressed
    /\ ElevatorState' = [ElevatorState EXCEPT ![e] = [@ EXCEPT !.doorsOpen = TRUE, !.buttonsPressed = @ \ {eState.floor}]]
    /\ ActiveElevatorCalls' = ActiveElevatorCalls \ {[floor |-> eState.floor, direction |-> eState.direction]}
    /\ UNCHANGED <<PersonState>>
    
EnterElevator(e) == \* All people on this floor who are waiting for the elevator and travelling the same direction enter the elevator.
    LET eState == ElevatorState[e] IN
    LET gettingOn == PeopleWaiting[eState.floor, eState.direction] IN
    LET destinations == {PersonState[p].destination : p \in gettingOn} IN
    /\ eState.doorsOpen
    /\ eState.direction /= "Stationary"
    /\ gettingOn /= {}
    /\ PersonState' = [p \in Person |->
        IF p \in gettingOn
        THEN [PersonState[p] EXCEPT !.location = e]
        ELSE PersonState[p]]
    /\ ElevatorState' = [ElevatorState EXCEPT ![e] = [@ EXCEPT !.buttonsPressed = @ \cup destinations]]
    /\ UNCHANGED <<ActiveElevatorCalls>>

ExitElevator(e) ==  \* All people whose destination is this floor exit the elevator.
    LET eState == ElevatorState[e] IN
    LET gettingOff == {p \in Person : PersonState[p].location = e /\ PersonState[p].destination = eState.floor} IN
    /\ eState.doorsOpen
    /\ gettingOff /= {}
    /\ PersonState' = [p \in Person |->
        IF p \in gettingOff
        THEN [PersonState[p] EXCEPT !.location = eState.floor, !.waiting = FALSE]
        ELSE PersonState[p]]
    /\ UNCHANGED <<ActiveElevatorCalls, ElevatorState>>

CloseElevatorDoors(e) ==    \* Close the elevator doors once all people have entered and exited the elevator on this floor.
    LET eState == ElevatorState[e] IN
    /\ ~ENABLED EnterElevator(e)
    /\ ~ENABLED ExitElevator(e)
    /\ eState.doorsOpen
    /\ ElevatorState' = [ElevatorState EXCEPT ![e] = [@ EXCEPT !.doorsOpen = FALSE]]
    /\ UNCHANGED <<PersonState, ActiveElevatorCalls>>

MoveElevator(e) ==  \* Move the elevator to the next floor unless we have to open the doors here.
    LET eState == ElevatorState[e] IN
    LET nextFloor == IF eState.direction = "Up" THEN eState.floor + 1 ELSE eState.floor - 1 IN
    /\ eState.direction /= "Stationary"
    /\ ~eState.doorsOpen
    /\ eState.floor \notin eState.buttonsPressed
    /\ \A call \in ActiveElevatorCalls : \* Can move only if other elevator servicing call
        /\ CanServiceCall[e, call] =>
            /\ \E e2 \in Elevator :
                /\ e /= e2
                /\ CanServiceCall[e2, call]
    /\ nextFloor \in Floor
    /\ ElevatorState' = [ElevatorState EXCEPT ![e] = [@ EXCEPT !.floor = nextFloor]]
    /\ UNCHANGED <<PersonState, ActiveElevatorCalls>>

StopElevator(e) == \* Stops the elevator if it's moved as far as it can in one direction
    LET eState == ElevatorState[e] IN
    LET nextFloor == IF eState.direction = "Up" THEN eState.floor + 1 ELSE eState.floor - 1 IN
    /\ ~ENABLED OpenElevatorDoors(e)
    /\ ~eState.doorsOpen
    /\ nextFloor \notin Floor
    /\ ElevatorState' = [ElevatorState EXCEPT ![e] = [@ EXCEPT !.direction = "Stationary"]]
    /\ UNCHANGED <<PersonState, ActiveElevatorCalls>>

(***************************************************************************)
(* This action chooses an elevator to service the call. The simple         *)
(* algorithm picks the closest elevator which is either stationary or      *)
(* already moving toward the call floor in the same direction as the call. *)
(* The system keeps no record of assigning an elevator to service a call.  *)
(* It is possible no elevator is able to service a call, but we are        *)
(* guaranteed an elevator will eventually become available.                *)
(***************************************************************************)
DispatchElevator(c) ==
    LET stationary == {e \in Elevator : ElevatorState[e].direction = "Stationary"} IN
    LET approaching == {e \in Elevator :
        /\ ElevatorState[e].direction = c.direction
        /\  \/ ElevatorState[e].floor = c.floor
            \/ GetDirection[ElevatorState[e].floor, c.floor] = c.direction } IN
    /\ c \in ActiveElevatorCalls
    /\ stationary \cup approaching /= {}
    /\ ElevatorState' = 
        LET closest == CHOOSE e \in stationary \cup approaching :
            /\ \A e2 \in stationary \cup approaching :
                /\ GetDistance[ElevatorState[e].floor, c.floor] <= GetDistance[ElevatorState[e2].floor, c.floor] IN
        IF closest \in stationary
        THEN [ElevatorState EXCEPT ![closest] = [@ EXCEPT !.floor = c.floor, !.direction = c.direction]]
        ELSE ElevatorState
    /\ UNCHANGED <<PersonState, ActiveElevatorCalls>>

Init == \* Initializes people and elevators to arbitrary floors
    /\ PersonState \in [Person -> [location : Floor, destination : Floor, waiting : {FALSE}]]
    /\ ActiveElevatorCalls = {}
    /\ ElevatorState \in [Elevator -> [floor : Floor, direction : {"Stationary"}, doorsOpen : {FALSE}, buttonsPressed : {{}}]]

Next == \* The next-state relation
    \/ \E p \in Person : PickNewDestination(p)
    \/ \E p \in Person : CallElevator(p)
    \/ \E e \in Elevator : OpenElevatorDoors(e)
    \/ \E e \in Elevator : EnterElevator(e)
    \/ \E e \in Elevator : ExitElevator(e)
    \/ \E e \in Elevator : CloseElevatorDoors(e)
    \/ \E e \in Elevator : MoveElevator(e)
    \/ \E e \in Elevator : StopElevator(e)
    \/ \E c \in ElevatorCall : DispatchElevator(c)

TemporalAssumptions ==  \* Assumptions about how elevators and people will behave
    /\ \A p \in Person : WF_Vars(CallElevator(p))
    /\ \A e \in Elevator : WF_Vars(OpenElevatorDoors(e))
    /\ \A e \in Elevator : WF_Vars(EnterElevator(e))
    /\ \A e \in Elevator : WF_Vars(ExitElevator(e))
    /\ \A e \in Elevator : SF_Vars(CloseElevatorDoors(e))
    /\ \A e \in Elevator : SF_Vars(MoveElevator(e))
    /\ \A e \in Elevator : WF_Vars(StopElevator(e))
    /\ \A c \in ElevatorCall : SF_Vars(DispatchElevator(c))

Spec == \* Initialize state with Init and transition with Next, subject to TemporalAssumptions
    /\ Init
    /\ [][Next]_Vars
    /\ TemporalAssumptions

THEOREM Spec => [](TypeInvariant /\ SafetyInvariant /\ TemporalInvariant)

=============================================================================

関連項目

[編集]

脚注

[編集]
  1. ^ Lamport, Leslie (January 2000). Specifying Concurrent Systems with TLA+. 173. IOS Press, Amsterdam. 183–247. ISBN 978-90-5199-459-9. http://research.microsoft.com/en-us/um/people/lamport/pubs/lamport-spec-tla-plus.pdf 22 May 2015閲覧。 
  2. ^ Lamport, Leslie (15 January 2014). “TLA+2: A Preliminary Guide”. 2 May 2015閲覧。
  3. ^ “Tlaplus Tools - License”. CodePlex. Microsoft, Compaq (8 April 2013). 10 May 2015閲覧。
  4. ^ a b Newcombe (29 September 2014). “Use of Formal Methods at Amazon Web Services”. Amazon. 8 May 2015閲覧。
  5. ^ Lamport, Leslie (25 January 2013). “Why We Should Build Software Like We Build Houses”. Wired (Wired). https://www.wired.com/2013/01/code-bugs-programming-why-we-need-specs/ 7 May 2015閲覧。. 
  6. ^ Lamport, Leslie (18 June 2002). “7.1 Why Specify”. Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers. Addison-Wesley. p. 75. ISBN 978-0-321-14306-8. http://research.microsoft.com/en-us/um/people/lamport/tla/book.html. "Having to describe a design precisely often reveals problems - subtle interactions and "corner cases" that are easily overlooked." 
  7. ^ Lamport, Leslie (2012). “How to Write a 21st Century Proof”. Journal of Fixed Point Theory and Applications 11: 43–63. doi:10.1007/s11784-012-0071-6. ISSN 1661-7738. http://research.microsoft.com/en-us/um/people/lamport/pubs/proof.pdf 23 May 2015閲覧。. 
  8. ^ Øhrstrøm, Peter; Hasle, Per (1995). “3.7 Temporal Logic and Computer Science”. Temporal Logic: From Ancient Ideas to Artificial Intelligence. Studies in Linguistics and Philosophy. 57. Springer Netherlands. pp. 344–365. doi:10.1007/978-0-585-37463-5. ISBN 978-0-7923-3586-3 
  9. ^ Lamport. “The Writings of Leslie Lamport: Proving the Correctness of Multiprocess Programs”. 22 May 2015閲覧。
  10. ^ Lamport. “The Writings of Leslie Lamport: On-the-fly Garbage Collection: an Exercise in Cooperation”. 22 May 2015閲覧。
  11. ^ Lamport. “The Writings of Leslie Lamport: 'Sometime' is Sometimes 'Not Never'”. 22 May 2015閲覧。
  12. ^ Lamport. “The Writings of Leslie Lamport: Specifying Concurrent Programming Modules”. 22 May 2015閲覧。
  13. ^ Lamport. “The Writings of Leslie Lamport: The Temporal Logic of Actions”. 22 May 2015閲覧。
  14. ^ a b Yu, Yuan; Manolios, Panagiotis; Lamport, Leslie (1999). Model checking TLA+ specifications. Lecture Notes in Computer Science. 1703. Springer-Verlag. 54–66. doi:10.1007/3-540-48153-2_6. ISBN 978-3-540-66559-5. http://research.microsoft.com/en-us/um/people/lamport/pubs/yuanyu-model-checking.pdf 14 May 2015閲覧。 
  15. ^ Lamport, Leslie (18 June 2002). Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers. Addison-Wesley. ISBN 978-0-321-14306-8. http://research.microsoft.com/en-us/um/people/lamport/tla/book.html 
  16. ^ Lamport, Leslie (2 January 2009). The PlusCal Algorithm Language. 5684. Springer Berlin Heidelberg. 36–60. doi:10.1007/978-3-642-03466-4_2. ISBN 978-3-642-03465-7. http://research.microsoft.com/en-us/um/people/lamport/pubs/pluscal.pdf 10 May 2015閲覧。 
  17. ^ a b c d Cousineau, Denis; Doligez, Damien; Lamport, Leslie; Merz, Stephan; Ricketts, Daniel; Vanzetto, Hernán (1 January 2012). TLA+ Proofs. Lecture Notes in Computer Science. 7436. Springer Berlin Heidelberg. 147–154. doi:10.1007/978-3-642-32759-9_14. ISBN 978-3-642-32758-2. http://research.microsoft.com/en-us/um/people/lamport/pubs/tlaps.pdf 14 May 2015閲覧。 
  18. ^ Lamport, Leslie (18 June 2002). “8.9.2 Machine Closure”. Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers. Addison-Wesley. p. 112. ISBN 978-0-321-14306-8. http://research.microsoft.com/en-us/um/people/lamport/tla/book.html. "We seldom want to write a specification that isn't machine closed. If we do write one, it's usually by mistake." 
  19. ^ Lamport, Leslie (18 June 2002). “8.9.6 Temporal Logic Considered Confusing”. Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers. Addison-Wesley. p. 116. ISBN 978-0-321-14306-8. http://research.microsoft.com/en-us/um/people/lamport/tla/book.html. "Indeed, [most engineers] can get along quite well with specifications of the form (8.38) that express only safety properties and don't hide any variables." 
  20. ^ Markus A. Kuppe (3 June 2014). Distributed TLC. TLA+ Community Event 2014, Toulouse, France.
  21. ^ “Unsupported TLAPS features”. TLA+ Proof System. Microsoft Research - INRIA Joint Centre. 14 May 2015閲覧。
  22. ^ TLA+ Proof System
  23. ^ Leslie Lamport (3 April 2014). Thinking for Programmers (at 21m46s). San Francisco: Microsoft. 2015年5月14日閲覧。
  24. ^ Lardinois (10 May 2017). “With Cosmos DB, Microsoft wants to build one database to rule them all”. TechCrunch. 10 May 2017閲覧。
  25. ^ Leslie Lamport (10 May 2017). Foundations of Azure Cosmos DB with Dr. Leslie Lamport. Microsoft Azure. 2017年5月10日閲覧。

外部リンク

[編集]
「https://ja-two.iwiki.icu/w/index.php?title=TLA%2B&oldid=92150818」から取得