超直方体
表示
(超矩形から転送)
この項目の現在の内容は百科事典というよりは辞書に適しています。 |
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2021年8月) 翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|
| Hyperrectangle
Orthotope | |
|---|---|
 A rectangular cuboid is a 3-orthotope A rectangular cuboid is a 3-orthotope
| |
| Type | Prism |
| Facets | 2n |
| Vertices | 2n |
| Schläfli symbol | {} × {} ... × {}[1] |
| Coxeter-Dynkin diagram | |
| Symmetry group | [2n−1], order 2n |
| Dual | Rectangular n-fusil |
| Properties | convex, zonohedron, isogonal |
幾何学における超直方体[2](ちょうちょくほうたい、英:hyperrectangle, orthotope)とは、長方形や直方体をより高次元に一般化したものである。形式的には区間のデカルト積として定義される。
すべての辺の長さが等しい超直方体は超立方体と呼ばれる。また、超立方体は超多面体、特に平行超多面体(英語: parallelotope)の特別な場合である。
定義
[編集]とし、 を なる任意の実数 とするとき、を( 次元の)超直方体という。
タイプ
[編集]双対多面体
[編集]| n-fusil | |
|---|---|
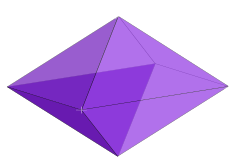 Example: 3-fusil Example: 3-fusil
| |
| Facets | 2n |
| Vertices | 2n |
| Schläfli symbol | {} + {} + ... + {} |
| Coxeter-Dynkin diagram | |
| Symmetry group | [2n−1], order 2n |
| Dual | n-orthotope |
| Properties | convex, isotopal |
| n | Example image |
|---|---|
| 1 | |
| 2 | 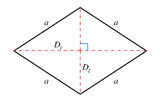 { } + { } { } + { } |
| 3 | 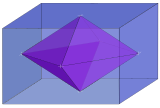 Rhombic 3-orthoplex inside 3-orthotope Rhombic 3-orthoplex inside 3-orthotope
{ } + { } + { }
|
脚注
[編集]- ^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.5 Spherical Coxeter groups, p.251
- ^ Coxeter, Harold Scott MacDonald (1973). Regular Polytopes (3rd ed.). New York: Dover. pp. 122–123. ISBN 0-486-61480-8
関連項目
[編集]外部リンク
[編集]- Weisstein, Eric W. "Rectangular parallelepiped". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Orthotope". mathworld.wolfram.com (英語).





![{\displaystyle \prod _{i=1}^{n}[a_{i},b_{i}]\quad \left(=\left\{(x_{1},\ldots ,x_{n})\in \mathbb {R} ^{n}\mid a_{i}\leq x_{i}\leq b_{i}\;(i=1,\ldots ,n)\right\}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2399e6760af6d54746e1b2d4d28482e352f0d978)

