利用者:Naelocevty/sandbox

加加加速度 jounce,snap
量記号	s
次元	L T −4
種類	ベクトル
SI単位	メートル毎秒毎秒毎秒毎秒 (m/s4)
CGS単位	センチメートル毎秒毎秒毎秒毎秒 (cm/s4)

加加加速度（かかかそくど, 英: jounce）、スナップ（英: snap）は、単位時間あたりの加加速度（躍度）の変化率である。説明や文中では躍度の勾配、躍度の変化度と表現されることがある。

国内にて実用例が確認される単位であり、種類は「ベクトルの時間4階微分」に分類される。

本項目では位置ベクトルの4段階微分の単位である「加加加速度（jounce,snap）」から、10段階微分の単位「put」までを紹介する。

概要

古典粒子の運動に関する量: 質量 m 、位置 r 、速度 v 、加速度 a

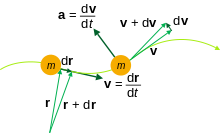
時間 t の関数である位置ベクトル r に対して、時間微分は t に関して計算することができる。これらの派生は、運動学、制御理論、工学および他の科学の研究において共通の有用性を有する。

速度

$\mathbf {v} ={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}$

加速度

$\mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}$

躍度（加加速度）

$\mathbf {j} ={\frac {\mathrm {d} \mathbf {a} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {v} }{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} }{\mathrm {d} t^{3}}}$

位置ベクトルの1階微分、2階微分、3階微分に対するこれらの名前（速度、加速度、躍度）は一般的に使用されている。

その拡張によって、高次の単位は同様の方法で計算することができる。これらの研究は、量の変位の近似を改善することができる。

加加加速度

英語圏ではsnap , jounceと呼ばれている。

$${\vec {s}}={\frac {d\,{\vec {\jmath }}}{dt}}={\frac {d^{2}{\vec {a}}}{dt^{2}}}={\frac {d^{3}{\vec {v}}}{dt^{3}}}={\frac {d^{4}{\vec {r}}}{dt^{4}}}$$

日本語の訳は躍度から先が特に定められていないが、英語での呼び方は定着している。上から順に「位置」「速度」「加速度」「躍度（加加速度）」「加加加速度」「加加加加速度」「加加加加加速度」……となる。

特に加加加速度が定数の場合には、以下の式が成り立つ。

${\vec {\jmath }}={\vec {\jmath }}_{0}+{\vec {s}}t,$

${\vec {a}}={\vec {a}}_{0}+{\vec {\jmath }}_{0}t+{\frac {1}{2}}{\vec {s}}t^{2},$

${\vec {v}}={\vec {v}}_{0}+{\vec {a}}_{0}t+{\frac {1}{2}}{\vec {\jmath }}_{0}t^{2}+{\frac {1}{6}}{\vec {s}}t^{3},$

${\vec {r}}={\vec {r}}_{0}+{\vec {v}}_{0}t+{\frac {1}{2}}{\vec {a}}_{0}t^{2}+{\frac {1}{6}}{\vec {\jmath }}_{0}t^{3}+{\frac {1}{24}}{\vec {s}}t^{4},$

ここで

${\vec {s}}$ は加加加速度,

${\vec {\jmath }}_{0}$ は初加加速度（初躍度）,

${\vec {\jmath }}$ は加加速度（躍度）,

${\vec {a}}_{0}$ は初加速度,

${\vec {a}}$ は加速度,

${\vec {v}}_{0}$ は初速度,

${\vec {v}}$ は速度,

${\vec {r}}_{0}$ は初期位置,

${\vec {r}}$ は位置,

$t$ は時間。

加加加速度の表記 ${\vec {s}}$ (ヴィザーらが論文で用いた表記）は、一般に同じ表記が用いられる変位ベクトルと混同しないように注意を要する。

加加加速度の次元は、[長さ]/[時間]⁴である。 国際単位系では、m/s⁴、あるいはm・s^-4が用いられ、CGS単位系では100G/s²もしくは100G・s⁻²に等しい。

使用例

加加速度（躍度）が時間でどのように変化していくか、その時間あたりの度合いを調べる際に使われる単位であり、滅多に日常的に使われるものではない。

しかし、CiNiiやJ-STAGEなどの日本語学術公開サイトでは使用例が数例のみあり、精密な宇宙工学や交通工学の分野での検証や地震の揺れ方の検証に用いられる。

• 工学系や力学系の一部として確立されている。れっきとした国際単位系の単位である。「加加加速度」と書かれることが少なく、英呼称の「snap」と表記されていることが多い。
• 電車や船の乗り物酔いの防止や、利用客の嘔吐中枢に過度の刺激を与えない絶叫マシンなどの、開発、研究段階で躍度とともにグラフで示される時が稀にある。
• 特に自動車会社ではこの加加加速度（snap）までであれば、大手メーカーでも使用されている例が多く、フリーソフトも配布されている。

その先の単位（5～6段階）

時間の関数としての加加加速度と位置の4、5、6、7、8、9、10段階微分は、「時にとても幾分な滑稽さを含んで」snap（躍度勾配、加加加速度）、 crackle（加加加加速度、躍度勾配の変化度）、 pop（加加加加加速度、単位時間当たりの躍度勾配の変化度）と呼ばれる。

また、その先の呼び方が存在しており、lock（加加加加加加速度、単位時間あたりのpopの変化度）、drop（加加加加加加加速度、単位時間当たりのlockの変化度）、shot（加加加加加加加加速度、単位時間当たりのdropの変化度）、put（加加加加加加加加加速度、単位時間当たりのshotの変化度）と呼ばれる。

論文の著者によると、5、6段階微分の単位名の俗称はケロッグのコーンシリアルの広告キャラクターの名前に触発されたとのこと。キャラクター自体の日本での呼称はそれぞれ「ピッチー」「パッチー」「プッチー」である。

しかし、位置の5段階以上の時間微分（crackle,flounce、加加加速度の変化、躍度の2段階微分以上の単位）が現れるのはほとんど稀であり、グラフ内にて「加」を4つ以上重ねた単位の呼称が個別にされる実例は漢字圏ではほとんど無い。

加加加加速度（crackle,flounce)

crackle(単位)は位置ベクトルを時間で5段階微分した、加加加速度の時間あたりの変化度の単位である。

日本語版Wikipediaでは、加加加加速度から先は「加」を増やして表記するがこれらは正式なものではない。

${\vec {c}}={\frac {d{\vec {s}}}{dt}}={\frac {d^{2}{\vec {\jmath }}}{dt^{2}}}={\frac {d^{3}{\vec {a}}}{dt^{3}}}={\frac {d^{4}{\vec {v}}}{dt^{4}}}={\frac {d^{5}{\vec {r}}}{dt^{5}}}$

この単位を定数c、時間を定数tと置くと次の式が成立する。

${\vec {s}}={\vec {s}}_{0}+{\vec {c}}\,t$

${\vec {\jmath }}={\vec {\jmath }}_{0}+{\vec {s}}_{0}\,t+{\tfrac {1}{2}}{\vec {c}}\,t^{2}$

${\vec {a}}={\vec {a}}_{0}+{\vec {\jmath }}_{0}\,t+{\tfrac {1}{2}}{\vec {s}}_{0}\,t^{2}+{\tfrac {1}{6}}{\vec {c}}\,t^{3}$

${\vec {v}}={\vec {v}}_{0}+{\vec {a}}_{0}\,t+{\tfrac {1}{2}}{\vec {\jmath }}_{0}\,t^{2}+{\tfrac {1}{6}}{\vec {s}}_{0}\,t^{3}+{\tfrac {1}{24}}{\vec {c}}\,t^{4}$

${\vec {r}}={\vec {r}}_{0}+{\vec {v}}_{0}\,t+{\tfrac {1}{2}}{\vec {a}}_{0}\,t^{2}+{\tfrac {1}{6}}{\vec {\jmath }}_{0}\,t^{3}+{\tfrac {1}{24}}{\vec {s}}_{0}\,t^{4}+{\tfrac {1}{120}}{\vec {c}}\,t^{5}$

このとき、

${\vec {c}}$ :加加加速度の変化度

${\vec {s}}_{0}$:加加加速度の変化度の初期値

${\vec {s}}$ :加加加速度

${\vec {\jmath }}_{0}$ :初加加速度（初躍度）

${\vec {\jmath }}$ :加加速度（躍度）

${\vec {a}}_{0}$:初加速度

${\vec {a}}$: ,加速度

${\vec {v}}_{0}$: 初速度

${\vec {v}}$: 速度

${\vec {r}}_{0}$: 初期位置

${\vec {r}}$: 位置

$t$: 時間

加加加速度の変化度の次元は、 L/T⁻⁵と表せる。これは 1m/s⁵ または100 G/s³と書かれる。

加加加加加速度（pop、pounce）

pop（単位）は位置ベクトルを時間で6段階微分した単位である。加加加加速度の時間当たりの変化度の単位であり「加加加加加速度」と呼ばれる。加加加速度の微分、躍度（加加速度）の2段階微分、加速度の3段階微分の単位である。

加加加加加速度が定数pとおける時、以下の等式が成り立つ。

${\vec {p}}={\frac {d{\vec {c}}}{dt}}={\frac {d^{2}{\vec {s}}}{dt^{2}}}={\frac {d^{3}{\vec {\jmath }}}{dt^{3}}}={\frac {d^{4}{\vec {a}}}{dt^{4}}}={\frac {d^{5}{\vec {v}}}{dt^{5}}}={\frac {d^{6}{\vec {r}}}{dt^{6}}}$

${\vec {c}}={\vec {c}}_{0}+{\vec {p}}\,t$

${\vec {s}}={\vec {s}}_{0}+{\vec {c}}_{0}\,t+{\tfrac {1}{2}}{\vec {p}}\,t^{2}$

${\vec {\jmath }}={\vec {\jmath }}_{0}+{\vec {s}}_{0}\,t+{\tfrac {1}{2}}{\vec {c}}_{0}\,t^{2}+{\tfrac {1}{6}}{\vec {p}}\,t^{3}$

${\vec {a}}={\vec {a}}_{0}+{\vec {\jmath }}_{0}\,t+{\tfrac {1}{2}}{\vec {s}}_{0}\,t^{2}+{\tfrac {1}{6}}{\vec {c}}_{0}\,t^{3}+{\tfrac {1}{24}}{\vec {p}}\,t^{4}$

${\vec {v}}={\vec {v}}_{0}+{\vec {a}}_{0}\,t+{\tfrac {1}{2}}{\vec {\jmath }}_{0}\,t^{2}+{\tfrac {1}{6}}{\vec {s}}_{0}\,t^{3}+{\tfrac {1}{24}}{\vec {c}}_{0}\,t^{4}+{\tfrac {1}{120}}{\vec {p}}\,t^{5}$

${\vec {r}}={\vec {r}}_{0}+{\vec {v}}_{0}\,t+{\tfrac {1}{2}}{\vec {a}}_{0}\,t^{2}+{\tfrac {1}{6}}{\vec {\jmath }}_{0}\,t^{3}+{\tfrac {1}{24}}{\vec {s}}_{0}\,t^{4}+{\tfrac {1}{120}}{\vec {c}}_{0}\,t^{5}+{\tfrac {1}{720}}{\vec {p}}\,t^{6}$

このとき

${\vec {p}}$: 加加加加加速度

${\vec {c}}_{0}$: 初加加加加速度

${\vec {c}}$: 加加加加速度

${\vec {s}}_{0}$: 初加加加速度

${\vec {s}}$: 加加加速度

${\vec {\jmath }}_{0}$: 初加加速度（初躍度）

${\vec {\jmath }}$: 加加速度（躍度）

${\vec {a}}_{0}$: 初加速度

${\vec {a}}$: 加速度

${\vec {v}}_{0}$: 初速度

${\vec {v}}$: 速度

${\vec {r}}_{0}$: 初期位置

${\vec {r}}$: 位置

$t$: 時間

加加加加加速度の次元はLT⁻⁶。単位は1m/s⁶、100G/s⁴である。

さらに先の単位（7～10段階）

加加加加加加速度（lock）

加加加加加加速度（lock）は位置ベクトルを時間で7段階微分した単位であり、加加加加加速度（pop）の時間あたりの変化率を表す単位。

加加加加速度（crackle）の2段階微分単位、加加加速度（jounce）の3段階微分単位、加加速度（jerk）の4段階微分単位、加速度の5段階微分単位、速度の6段階微分単位。

加加加加加加速度の次元はLT⁻⁷。単位は1m/s⁷、100G/s⁵である。

加加加加加加加速度（drop）

加加加加加加加速度（drop）は位置ベクトルを時間で8段階微分した単位であり、加加加加加加速度（lock）の時間あたりの変化率を表す単位。

加加加加加速度（pop）の2段階微分単位、加加加加速度（crackle）の3段階微分単位、加加加速度（jounce）の4段階微分単位、加加速度（jerk）の5段階微分単位、加速度の6段階微分単位、速度の7段階微分単位。

加加加加加加加速度の次元はLT⁻⁸。単位は1m/s⁸、100G/s⁶である。

加加加加加加加加速度（shot）

加加加加加加加加加速度（shot）は位置ベクトルを時間で9段階微分した単位であり、加加加加加加加速度（drop）の時間あたりの変化率を表す単位。

加加加加加加加速度（lock）の2段階微分単位、加加加加加加速度（pop）の3段階微分単位、加加加加速度（crackle）の4段階微分単位、加加加速度（jounce）の5段階微分単位、加加速度（jerk）の6段階微分単位、加速度の7段階微分単位、速度の8段階微分単位ともいえる。

加加加加加加加速度の次元はLT⁻⁹。単位は1m/s⁹、100G/s⁷である。

加加加加加加加加加速度（put）

加加加加加加加加加速度（put）は位置ベクトルを時間で10段階微分した単位であり、加加加加加加加加速度（shot）の時間あたりの変化率を表す単位。

加加加加加加加加速度（shot）の2段階微分単位、加加加加加加加速度（lock）の3段階微分単位、加加加加加加速度（pop）の4段階微分単位、加加加加速度（crackle）の5段階微分単位、加加加速度（jounce）の6段階微分単位、加加速度（jerk）の7段階微分単位、加速度の8段階微分単位、速度の9段階微分単位ともいえる。

加加加加加加加速度の次元はLT⁻¹⁰。単位は1m/s¹⁰、100G/s⁸である。

11次元以上の場合

一般的な学術論文でも使われることは無いと言っていい。

位置ベクトルの単位時間における導関数の次元は通常の数（非負整数）に対して定義される。国際単位系における単位次元はLT⁻¹¹、LT⁻¹²・・・と増えるが、それらの呼称は英語圏でも決められていない。

参考文献

外部リンク

• Cosmography: cosmology without the Einstein equations, Matt Visser, School of Mathematics, Statistics and Computer Science, Victoria University of Wellington, 2004.

関連項目

• 運動生理学
• スポーツ科学
• 乗り物酔い - この加加加速度と躍度が大いに関係する。
• 運動方程式
• はじきの法則 - 小学生が速度の関係を学ぶ際によく使われる円状のグラフの通称。