「二次構造」の版間の差分
m →関連項目 |
編集の要約なし |
||
| (8人の利用者による、間の15版が非表示) | |||
| 1行目: | 1行目: | ||
{{Otheruses|タンパク質の二次構造|核酸の二次構造|核酸二次構造}} |
|||
| ⚫ | |||
{{タンパク質構造}} |
|||
| ⚫ | |||
'''タンパク質の二次構造'''は、タンパク質の「局所区分」の3次元[[配座異性|構造]]である。最も一般的な2種類の二次構造要素は[[αヘリックス]]と[[βシート]]であるが、[[βターン]]や[[ωループ]]も見られる。二次構造要素は通常、タンパク質が[[三次構造]]へと[[フォールディング|折り畳まれる]]前の中間状態として自発的に形成される。 |
|||
二次構造はペプチド[[主鎖]]中のアミド水素原子とカルボニル酸素原子との間の[[水素結合]]のパターンによって形式的に定義される。二次構造は別法として、正しい水素結合を持っているかどうかにかかわらず、[[ラマチャンドラン・プロット]]の特定の領域における主鎖の[[二面角]]の規則的なパターンに基づいて定義することもできる。 |
|||
二次構造の概念は1952年に[[スタンフォード大学]]の[[カイ・ウルリク・リンデルストロム=ラング]]によって初めて発表された<ref>{{cite book | author = Linderstrøm-Lang KU | title = Lane Medical Lectures: Proteins and Enzymes | year = 1952 | publisher = Stanford University Press | pages = 115 | asin = B0007J31SC}}</ref><ref name="pmid9144781">{{cite journal | vauthors = Schellman JA, Schellman CG | title = Kaj Ulrik Linderstrøm-Lang (1896–1959) | journal = Protein Sci. | volume = 6 | issue = 5 | pages = 1092–100 | year = 1997 | pmid = 9144781 | pmc = 2143695 | doi = 10.1002/pro.5560060516 | quote = He had already introduced the concepts of the primary, secondary, and tertiary structure of proteins in the third Lane Lecture (Linderstram-Lang, 1952) }}</ref>。核酸といったその他の[[生体高分子]]も特徴的な[[核酸の二次構造|二次構造]]を有する。 |
|||
== 種類 == |
|||
{| class="wikitable sortable floatright" |
|||
|+ 主要な3種類のタンパク質らせん構造<ref>{{cite web | url = http://www.biomed.curtin.edu.au/biochem/tutorials/prottute/helices.htm | title = Interactive Protein Structure Tutorial | author = Steven Bottomley | year = 2004 | accessdate = January 9, 2011 }}</ref> |
|||
!幾何配置の特性 |
|||
!αヘリックス |
|||
!3<sub>10</sub>ヘリックス |
|||
!πヘリックス |
|||
|- |
|||
|回転毎の残基 ||align="right"| 3.6 ||align="right"| 3.0 ||align="right"| 4.4 |
|||
|- |
|||
| 残基毎の並進 ||align="right"| {{convert|1.5|Å|nm|abbr=on}} ||align="right"| {{convert|2.0|Å|nm|abbr=on}} ||align="right"| {{convert|1.1|Å|nm|abbr=on}} |
|||
|- |
|||
|らせんの半径 ||align="right"| {{convert|2.3|Å|nm|abbr=on}} ||align="right"| {{convert|1.9|Å|nm|abbr=on}} ||align="right"| {{convert|2.8|Å|nm|abbr=on}} |
|||
|- |
|||
|間隔幅 ||align="right"| {{convert|5.4|Å|nm|abbr=on}} ||align="right"| {{convert|6.0|Å|nm|abbr=on}} <!-- 3.0 r/t * 2.0Å trans --> ||align="right"| {{convert|4.8|Å|nm|abbr=on}} <!-- 4.4 r/t * 1.1Å trans --> |
|||
|} |
|||
最も一般的な二次構造は[[αヘリックス]]と[[βシート]]である。[[310ヘリックス|3<sub>10</sub>ヘリックス]]および[[πヘリックス]]といったその他のらせんはエネルギー的に好ましい水素結合パターンを持つと計算されるが、ヘリックスの中心における不利な主鎖の詰め込みのためαヘリックスの末端を除いては天然のタンパク質ではめったに見られない。[[ポリプロリンヘリックス]]および[[αシート]]といったその他の伸長構造は[[天然状態]]のタンパク質では希であるが、タンパク質の[[フォールディング|折り畳み]]の重要な中間体としてしばしば仮定されている。締まった[[ターン (生化学)|ターン]]と緩く柔軟なループはより「常連」の二次構造要素を繋ぐ。[[ランダムコイル]]は真の二次構造ではないが、正規の二次構造の欠如を示すコンホメーションの一分類である。 |
|||
[[アミノ酸]]は様々な二次構造要素を構成する能力にそれぞれ違いがある。[[プロリン]]および[[グリシン]]はαヘリックス主鎖の規則性を混乱させるため「ヘリックスブレイカー」と呼ばれることがある。しかしながら、どちらのアミノ酸も特有の立体配座能を有しており、ターン中でよく見られる。タンパク質中で[[αヘリックス|らせん]]配座を取りやすいアミノ酸には、[[メチオニン]]、[[アラニン]]、[[ロイシン]]、[[グルタミン]]、[[リシン]]がある(アミノ酸の1文字表記で "MALEK")。対照的に、大きな芳香族残基([[トリプトファン]]、[[チロシン]]、[[フェニルアラニン]])およびC<sup>β</sup>-分岐アミノ酸([[イソロイシン]]、[[バリン]]、[[スレオニン]])は[[βシート|β鎖]]配座を取りやすい。しかしながら、これらの傾向は、配列のみから二次構造を予測する信頼性のある手法を確立できるほど強いわけではない。 |
|||
低周波集団振動はタンパク質内の局部剛性に敏感であると考えられており、β構造はα構造あるいは不規則タンパク質よりも一般的に剛直であることが明らかにされている<ref>{{cite journal | vauthors = Perticaroli S, Nickels JD, Ehlers G, O'Neill H, Zhang Q, Sokolov AP | title = Secondary structure and rigidity in model proteins | journal = Soft Matter | volume = 9 | issue = 40 | pages = 9548–56 | date = October 2013 | pmid = 26029761 | doi = 10.1039/C3SM50807B }}</ref><ref>{{cite journal | vauthors = Perticaroli S, Nickels JD, Ehlers G, Sokolov AP | title = Rigidity, secondary structure, and the universality of the boson peak in proteins | journal = Biophysical Journal | volume = 106 | issue = 12 | pages = 2667–74 | date = June 2014 | pmid = 24940784 | pmc = 4070067 | doi = 10.1016/j.bpj.2014.05.009 }}</ref>。中性子散乱測定は~1 THzのスペクトル特性を[[βバレル]]タンパク質[[GFP]]の二次構造の集団運動を直接的に結び付けた<ref>{{cite journal | vauthors = Nickels JD, Perticaroli S, O'Neill H, Zhang Q, Ehlers G, Sokolov AP | title = Coherent neutron scattering and collective dynamics in the protein, GFP | journal = Biophys. J. | volume = 105 | issue = 9 | pages = 2182–87 | year = 2013 | pmid = 24209864 | pmc = 3824694 | doi = 10.1016/j.bpj.2013.09.029 }}</ref>。 |
|||
二次構造中の水素結合パターンは大きくゆがんでおり、これが二次構造の自動的な決定を困難にしている。タンパク質二次構造を形式的に決定する手法はいくつか存在する(例: [[DSSP (水素結合推定アルゴリズム)|DSSP]]<ref>{{cite journal | vauthors = Kabsch W, Sander C | title = Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features | journal = Biopolymers | volume = 22 | issue = 12 | pages = 2577–637 | date = Dec 1983 | pmid = 6667333 | doi = 10.1002/bip.360221211 }}</ref>、DEFINE<ref>{{cite journal | vauthors = Richards FM, Kundrot CE | title = Identification of structural motifs from protein coordinate data: secondary structure and first-level supersecondary structure | journal = Proteins | volume = 3 | issue = 2 | pages = 71–84 | year = 1988 | pmid = 3399495 | doi = 10.1002/prot.340030202 }}</ref>、[[STRIDE]]<ref>{{cite journal | vauthors = Frishman D, Argos P | title = Knowledge-based protein secondary structure assignment | journal = Proteins | volume = 23 | issue = 4 | pages = 566–79 | date = Dec 1995 | pmid = 8749853 | doi = 10.1002/prot.340230412 | url = http://nook.cs.ucdavis.edu/~koehl/Classes/ECS289/reprints/Paper_Stride.pdf }}</ref>、ScrewFit<ref>{{Cite journal|last=Calligari|first=Paolo A.|last2=Kneller|first2=Gerald R.|date=2012-12-01|title=ScrewFit: combining localization and description of protein secondary structure|url=https://doi.org/10.1107/S0907444912039029|journal=Acta Crystallographica Section D|language=en|volume=68|issue=12|pages=1690–1693|doi=10.1107/s0907444912039029|issn=0907-4449}}</ref>、SST<ref>{{cite web|url=http://lcb.infotech.monash.edu.au/sstweb2|title=SST: Protein Secondary structural assignment using Minimum Message Length inference|publisher=Laboratory of Computational Biology, Monash University|author=Arun Konagurthu |accessdate=2018-01-04}}</ref><ref>{{cite journal | vauthors = Konagurthu AS, Lesk AM, Allison L | title = Minimum message length inference of secondary structure from protein coordinate data | journal = Bioinformatics | volume = 28 | issue = 12 | pages = i97–i105 | date = Jun 2012 | pmid = 22689785 | pmc = 3371855 | doi = 10.1093/bioinformatics/bts223 }}</ref>)。 |
|||
=== DSSP分類 === |
|||
{{Main article|DSSP (水素結合推定アルゴリズム)}} |
|||
[[Image:SegmentLengths.dist.png|thumb|200px|Non-redundant pdb_select dataset (March 2006) から得られた分布。二次構造はDSSPによって割り当てられた。8種類の配座状態は3つの状態へと縮小されている: H=HGI, E=EB, C=STC。]] |
|||
The Dictionary of Protein Secondary Structure(略称DSSP)は、一文字表記を使ってタンパク質二次構造を記述するために一般的に用いられている。二次構造は1951年(タンパク質構造が実験的に決定されるよりも前)にポーリングらによって提唱された水素結合パターンに基づいて割り当てられる。DSSPが定義する8種類の二次構造は以下の通りである。 |
|||
* G = 3-ターンヘリックス([[310ヘリックス|3<sub>10</sub>ヘリックス]])。最小長は3残基。 |
|||
* H = 4-ターンヘリックス([[αヘリックス]])。最小長は4残基。 |
|||
* I = 5-ターンヘリックス([[πヘリックス]])。最小長は5残基。 |
|||
* T = 水素結合したターン(3、4、5ターン) |
|||
* E = 平行あるいは逆平行[[βシート]]配座の伸長鎖。最小長は2残基。 |
|||
* B = 孤立したβブリッジ(単一ペアのβシート性水素結合形成)残基 |
|||
* S = ベンド(唯一、水素結合に基づかない割り当て) |
|||
* C = コイル(上記のいずれにも該当しない残基) |
|||
「コイル」はしばしば ' '(空白)、C (coil)、または '–'(ダッシュ)と表記される。ヘリックス(G、H、I)およびシート配座は全て妥当な長さを持つことを必要とする。これは、タンパク質構造中の2つの隣接した残基同じ水素結合パターンを形成しなければならないことを意味する。ヘリックス性またはシート性水素結合パターンが短かすぎる場合は、それぞれTまたはBと指定される。その他にも二次構造のカテゴリーは存在するが(鋭いターン、[[ωループ]]等)、めったに使われない。 |
|||
二次構造は[[水素結合]]によって定義されるため、水素結合の厳密な定義が決定的に重要な意味を持つ。二次構造に関する標準的な水素結合の定義はDSSPの定義であり、これは純粋に静電的なモデルである。DSSPはカルボニル炭素と酸素にそれぞれ±''q''<sub>1</sub> ≈ 0.42[[電気素量|''e'']]の電荷を、アミド水素と窒素にそれぞれ±''q''<sub>2</sub> ≈ 0.20''e''の電荷を割り当てる。静電エネルギーは |
|||
:<math> |
|||
E = q_{1} q_{2} |
|||
\left( \frac{1}{r_\mathrm{ON}} + \frac{1}{r_\mathrm{CH}} - \frac{1}{r_\mathrm{OH}} - \frac{1}{r_\mathrm{CN}} \right) \cdot 332 \text{ kcal/mol}. |
|||
</math> |
|||
である。 |
|||
DSSPによれば、''E''が{{cvt|-0.5|kcal/mol|kJ/mol}} より小さい時かつその時に限り水素結合が存在する。DSSPの式は「物理的」水素結合エネルギーの比較的粗い近似であるものの、二次構造を定義する道具として一般的に受け入れられている。 |
|||
== 実験的決定 == |
|||
生体高分子の大まかな二次構造含量(例えば、「このタンパク質は40%のαヘリックスと20%のβシートを含む」)は[[分光法]]により推定することができる<ref name="Pelton_ McLean_2000">{{cite journal | vauthors = Pelton JT, McLean LR | title = Spectroscopic methods for analysis of protein secondary structure | journal = Anal. Biochem. | volume = 277 | issue = 2 | pages = 167–76 | year = 2000 | pmid = 10625503 | doi = 10.1006/abio.1999.4320 }}</ref>。タンパク質に対しては、遠紫外(170–250 nm)[[円偏光二色性|円偏光二色性スペクトル測定]]が一般的な手法である。208および222 nmにおける目立った二重極小はαヘリックス構造を示すのに対して、204 nmまたは217 nmにおける単一極小はランダムコイルまたはβシート構造をそれぞれ反映している。水素結合によるアミド基の結合振動における違いを検出する手法である[[赤外分光法]]も用いられるがあまり一般的ではない。二次構造含量は[[核磁気共鳴|NMR]]スペクトルの[[化学シフト]]を使って正確に推定することができる<ref name="pmid14668443">{{cite journal | vauthors = Meiler J, Baker D | title = Rapid protein fold determination using unassigned NMR data | journal = Proc. Natl. Acad. Sci. U.S.A. | volume = 100 | issue = 26 | pages = 15404–09 | year = 2003 | pmid = 14668443 | pmc = 307580 | doi = 10.1073/pnas.2434121100 | url = }}</ref>。 |
|||
== 予測 == |
|||
{{See also|タンパク質構造予測}} |
|||
アミノ酸配列のみからタンパク質三次構造を予測することは非常に困難な問題であるが、より単純な二次構造の定義を用いることはより扱いやすい。 |
|||
初期の二次構造予測の手法では3つの主要な状態、ヘリックス、シート、またはランダムコイルを予測することしかできなかった。これらの手法は個々のアミノ酸のヘリックスまたはシートを形成する傾向に基づいており、二次構造要素形成の自由エネルギーを推定するための規則を組み合わせられることもあった。このような手法が残基が3つの状態(ヘリックス/シート/コイル)のどれを取るかの予測精度は概して~60%であった。アミノ酸配列から二次構造を予測するために最初に広く用いられた手法は{{仮リンク|シュー–ファスマン法|en|Chou–Fasman method}}であった<ref name="Chou_predict0">{{cite journal | vauthors = Chou PY, Fasman GD | title = Prediction of protein conformation | journal = Biochemistry | volume = 13 | issue = 2 | pages = 222–45 | date = Jan 1974 | pmid = 4358940 | doi = 10.1021/bi00699a002 }}</ref><ref name="Chou_predict1">{{cite journal | vauthors = Chou PY, Fasman GD | title = Empirical predictions of protein conformation | journal = Annu. Rev. Biochem.| volume = 47 | pages = 251–76 | year = 1978 | pmid = 354496 | doi = 10.1146/annurev.bi.47.070178.001343 }}</ref><ref name="Chou_predict2">{{cite journal | vauthors = Chou PY, Fasman GD | title = Prediction of the secondary structure of proteins from their amino acid sequence | journal = Adv. Enzymol. Relat. Areas Mol. Biol. | volume = 47 | pages = 45–148 | year = 1978 | pmid = 364941 | doi=10.1002/9780470122921.ch2}}</ref>。 |
|||
精度の著しい上昇(~80%近くまで)は[[多重整列|多重配列アラインメント]]を利用することによって成された。[[進化]]を通じてある位置(とその周辺、典型的には前後に~7残基)に存在するアミノ酸の完全な分布を知ることにより、その位置周辺の構造的傾向についてはるかに良い予想を立てることが可能になった<ref name="Simossis_2004">{{cite journal | vauthors = Simossis VA, Heringa J | title = Integrating protein secondary structure prediction and multiple sequence alignment | journal = Current Protein & Peptide Science | volume = 5 | issue = 4 | pages = 249–66 | date = Aug 2004 | pmid = 15320732 | doi = 10.2174/1389203043379675 }}</ref><ref name="pmid20221928">{{cite journal | vauthors = Pirovano W, Heringa J | title = Protein secondary structure prediction | journal = Methods Mol. Biol. | volume = 609 | issue = | pages = 327–48 | year = 2010 | pmid = 20221928 | doi = 10.1007/978-1-60327-241-4_19 }}</ref>。 |
|||
例えば、あるタンパク質がある位置に[[グリシン]]を持つとすると、それ自体はその位置にランダムコイルが存在することを示唆する。しかし、多重配列アラインメントにより、数十億年近くの進化を経ている相同タンパク質の95%においてヘリックスに多く含まれるアミノ酸がその位置(と近傍)に存在することを明らかにするかもしれない。さらに、その位置と近傍における平均[[疎水性]]を調べることによって、同じアラインメントがαヘリックスと一致した残基の{{仮リンク|溶媒接触可能表面積|en|Accessible surface area|lable=溶媒露出度}}のパターンをも示唆するかもしれない。これらの事実は元のタンパク質のグリシンがランダムコイルではなくαヘリックス構造に含まれることを示唆する。[[ニューラルネットワーク]]、[[隠れマルコフモデル]]、[[サポートベクターマシン]]を含む数種類の手法が、利用可能な全データを組み合わせ上記の3種の二次構造を予測するために用いられている。現代的な予測手法は、全ての位置における予測に対する信頼性スコアも提供する。 |
|||
二次構造予測手法は継続的に基準に従って評価された(例: {{仮リンク|EVA (ベンチマーク)|en|EVA (benchmark)|label=EVA}})。これらの試験に基づいた最も正確な手法は、{{仮リンク| PSIPRED|en| PSIPRED}}、SAM<ref name="pmid19483096">{{cite journal | vauthors = Karplus K | title = SAM-T08, HMM-based protein structure prediction | journal = Nucleic Acids Res. | volume = 37 | issue = Web Server issue | pages = W492–97 | year = 2009 | pmid = 19483096 | pmc = 2703928 | doi = 10.1093/nar/gkp403 }}</ref>、PORTER<ref name="pmid15585524">{{cite journal | vauthors = Pollastri G, McLysaght A | title = Porter: a new, accurate server for protein secondary structure prediction | journal = Bioinformatics | volume = 21 | issue = 8 | pages = 1719–20 | year = 2005 | pmid = 15585524 | doi = 10.1093/bioinformatics/bti203 }}</ref>、PROF<ref name="pmid24799431">{{cite journal | vauthors = Yachdav G, Kloppmann E, Kajan L, Hecht M, Goldberg T, Hamp T, Hönigschmid P, Schafferhans A, Roos M, Bernhofer M, Richter L, Ashkenazy H, Punta M, Schlessinger A, Bromberg Y, Schneider R, Vriend G, Sander C, Ben-Tal N, Rost B | title = PredictProtein—an open resource for online prediction of protein structural and functional features | journal = Nucleic Acids Res. | volume = 42 | issue = Web Server issue | pages = W337–43 | year = 2014 | pmid = 24799431 | pmc = 4086098 | doi = 10.1093/nar/gku366 | url = }}</ref>、SABLE<ref name="pmid15768403">{{cite journal | vauthors = Adamczak R, Porollo A, Meller J | title = Combining prediction of secondary structure and solvent accessibility in proteins | journal = Proteins | volume = 59 | issue = 3 | pages = 467–75 | year = 2005 | pmid = 15768403 | doi = 10.1002/prot.20441 | url = }}</ref>であった。改善のための根本的な領域はβ鎖の予測と考えられている。β鎖と確信を持って予測される残基についての精度は高いが、これらの手法は一部のβ鎖領域を見落としがちである(偽陰性)。PDB構造に対して二次構造クラス(ヘリックス/ストランド/コイル)を割り当てる標準手法(DSSPで割り当てられ、この二次構造に対する予測精度が評価される)の特異性のため、全体の予測精度には~90%の上限がありそうである<ref>{{cite journal | vauthors = Kihara D | title = The effect of long-range interactions on the secondary structure formation of proteins | journal = Protein Science | volume = 14 | issue = 8 | pages = 1955–963 | date = Aug 2005 | pmid = 15987894 | pmc = 2279307 | doi = 10.1110/ps.051479505 }}</ref>。 |
|||
最も単純な{{仮リンク|ホモロジーモデリング|en|Homology modeling}}の場合を除いて、正確な二次構造予測は[[三次構造]]の予測において鍵となる要素である。例えば、明確に予測された6つの二次構造要素のパターンβαββαβは[[フェレドキシン]]折り畳み構造の特徴である<ref name="pmid15558583">{{cite journal | vauthors = Qi Y, Grishin NV | title = Structural classification of thioredoxin-like fold proteins | journal = Proteins | volume = 58 | issue = 2 | pages = 376–88 | year = 2005 | pmid = 15558583 | doi = 10.1002/prot.20329 | url = http://prodata.swmed.edu/Lab/Thiored_Proteins04.pdf | quote = Since the fold definition should include only the core secondary structural elements that are present in the majority of homologs, we define the thioredoxin-like fold as a two-layer / sandwich with the βαββαβ secondary-structure pattern. }}</ref>。 |
|||
== 応用 == |
|||
タンパク質および核酸二次構造のどちらも多重配列アラインメントに利用でき、単純な配列情報に加えて二次構造の情報を含めることでより正確にアラインすることできる。RNAでは、塩基対が配列よりもかなり高度に保存されているためあまり役に立たない。一次構造がアラインできないほどに異なるタンパク質間の関係が二次構造の比較によって見出されることがある<ref name="Simossis_2004"/>。 |
|||
天然タンパク質において、αヘリックスはβストランドよりも安定で、変異に対して頑強で、設計可能であることが示されてきたことから<ref>{{cite journal | vauthors = Abrusan G, Marsh JA | title = Alpha helices are more robust to mutations than beta strands | journal = PLoS Computational Biology | volume = 12 | issue = 12 | pages = 1–16 | date = 2016 | pmid = 27935949 | doi = 10.1371/journal.pcbi.1005242 }}</ref>、全てがα-ヘリックスによって構成されている機能性タンパク質の設計はヘリックスとストランドの両方を持つタンパク質の設計よりも容易であると思われており、最近実験的に確かめられている<ref>{{cite journal | vauthors = Rocklin GJ et al. | title = Global analysis of protein folding using massively parallel design, synthesis, and testing | journal = Science | volume = 357 | issue = 6347 | pages = 168–175 | date = 2017 | pmid = 28706065 | doi = 10.1126/science.aan0693 }}</ref>。 |
|||
== ペプチド結合の構造 == |
== ペプチド結合の構造 == |
||
[[画像:Trans-peptide.PNG|thumb|right|300px|''trans''-ペプチド結合構造。長さの単位は[[オングストローム|Å]]]] |
[[画像:Trans-peptide.PNG|thumb|right|300px|''trans''-ペプチド結合構造。長さの単位は[[オングストローム|Å]]]] |
||
[[画像:Cis-peptide.PNG|thumb|right|300px|''cis''-ペプチド結合構造。長さの単位は[[オングストローム|Å]]]] |
[[画像:Cis-peptide.PNG|thumb|right|300px|''cis''-ペプチド結合構造。長さの単位は[[オングストローム|Å]]]] |
||
1930 |
1930-40年代、[[ライナス・ポーリング]]と[[ロバート・コリー]]は[[ポリペプチド]]鎖内において[[アミノ酸]]や[[ペプチド結合]]がどのような形状をしているのかを調べるため[[X線構造解析]]を行い、右図のような平面構造を取っていることを突き止めた。ペプチドのC-N結合はC<sub>α</sub>-N結合より0.13 Å短く、C=O結合が[[アルデヒド]]や[[ケトン]]のC=Oよりも0.02 Å短い事から次のように[[共鳴理論|共鳴]]していると考えられている。 |
||
[[画像:Peptide Resonance.PNG|center|300px]] |
[[画像:Peptide Resonance.PNG|center|300px]] |
||
ペプチド結合の[[共鳴エネルギー]]は平面のとき最大値(約 |
ペプチド結合の[[共鳴エネルギー]]は平面のとき最大値(約85 kJ/mol)をとり、平面から90° ねじれると共鳴エネルギーはゼロとなることからも平面構造が非常に強いことが分かる。ペプチド結合は普通トランス型をとり、隣接するC<sub>α</sub>同士は点対称の関係になる。シス型をとった場合、[[立体障害]]のためトランス型より約8 kJ/molだけ不安定になる。しかし、[[プロリン]]の手前のペプチドでは少しだけ安定化する。このためプロリンの手前のペプチドの約10%はシス型をとっている。 |
||
=== ポリペプチド主鎖の二面角 === |
=== ポリペプチド主鎖の二面角 === |
||
| 12行目: | 95行目: | ||
=== ラマチャンドランダイアグラム === |
=== ラマチャンドランダイアグラム === |
||
{{See also|ラマチャンドランプロット}} |
|||
[[Image:Ramaplot.png|thumb|right|200px|[[核内増殖抗原]](PCNA)のラマチャンドランダイアグラム。縦軸はψ、横軸はφ。青領域はふつう許容される範囲、緑領域は限界範囲。このグラフからもφ、ψのとりうる範囲は全体の25%程度であることが分かる。]] |
[[Image:Ramaplot.png|thumb|right|200px|[[核内増殖抗原]] (PCNA) のラマチャンドランダイアグラム。縦軸はψ、横軸はφ。青領域はふつう許容される範囲、緑領域は限界範囲。このグラフからもφ、ψのとりうる範囲は全体の25%程度であることが分かる。]] |
||
'''ラマチャンドランダイアグラム''' |
'''ラマチャンドランダイアグラム'''、'''[[ラマチャンドランプロット]]'''、または'''ラマチャンドランマップ'''とは、φ、ψ値、各原子間距離の計算によって立体的に許容されるペプチドの構造の範囲を図示したものである。 |
||
{| class="wikitable" style="margin:0 auto" |
{| class="wikitable" style="margin:0 auto" |
||
|+二次構造のφ、ψ値 |
|+二次構造のφ、ψ値 |
||
| 58行目: | 142行目: | ||
|- |
|- |
||
|} |
|} |
||
ラマチャンドランダイアグラムの示す構造可能範囲は各アミノ酸の側鎖の大きさによって変化する。例えば[[グリシン]]はC<sub>β</sub>が無いため他のアミノ酸に比べて許容範囲はずっと広い。また、[[プロリン]]の側鎖は環状であるため許容範囲は極端に制限される(φ= |
ラマチャンドランダイアグラムの示す構造可能範囲は各アミノ酸の側鎖の大きさによって変化する。例えば[[グリシン]]はC<sub>β</sub>が無いため他のアミノ酸に比べて許容範囲はずっと広い。また、[[プロリン]]の側鎖は環状であるため許容範囲は極端に制限される(φ = −60°±25°)。 |
||
== ヘリックス構造 == |
== ヘリックス構造 == |
||
ポリペプチド鎖の各C<sub>α</sub>炭素が同じようにねじれるとヘリックス([[螺旋]])構造をとる。ヘリックス構造はφ、ψではなく、1回転あたりの残基数(n:右巻きは正、左巻きは負)、1回転で軸方向に進む距離(ピッチ |
ポリペプチド鎖の各C<sub>α</sub>炭素が同じようにねじれるとヘリックス([[螺旋]])構造をとる。ヘリックス構造はφ、ψではなく、1回転あたりの残基数(n:右巻きは正、左巻きは負)、1回転で軸方向に進む距離(ピッチ、p)で表される。p=0のとき閉環となり、p=2のときは平面リボン構造をとる。 |
||
=== αヘリックス === |
=== αヘリックス === |
||
[[Image:AlphaHelixProtein fr.jpg|thumb|right|200px|αヘリックス]] |
[[Image:AlphaHelixProtein fr.jpg|thumb|right|200px|αヘリックス]] |
||
ポリペプチドのヘリックス構造の中で二面角と水素結合形成の双方を満足する構造は'''[[αヘリックス]]'''だけで、<small>L</small>-アミノ酸で作られるαヘリックスはφ= |
ポリペプチドのヘリックス構造の中で二面角と水素結合形成の双方を満足する構造は'''[[αヘリックス]]'''だけで、<small>L</small>-アミノ酸で作られるαヘリックスはφ=−57°、ψ=−47°、n=3.6、p=5.4 Åである。αヘリックスではすべての[[アミノ基|N-H]]基が4残基離れたアミノ酸の[[カルボニル基|C=O]]基へ水素結合をしている。このときのN…O間の距離は2.8 Åで、水素結合には適当であり、会合エネルギーも最大となる。右巻き構造では側鎖は外側を向いており主鎖にとっても相互にも障害にならない。しかし左巻き構造では側鎖が主鎖に近すぎるため作られることは少ない。 |
||
=== その他のヘリックス構造 === |
=== その他のヘリックス構造 === |
||
2.2<sub>7</sub>リボン、3<sub>10</sub>ヘリックスのようなn<sub>m</sub>という表示のnはヘリックス1回転あたりのアミノ酸残基数、mは[[水素結合]]で閉環した構造の[[水素]]原子を含む構成原子数を表している。αヘリックスをこの表記で書くと3.6<sub>13</sub>ヘリックスとなる。 |
2.2<sub>7</sub>リボン、3<sub>10</sub>ヘリックスのようなn<sub>m</sub>という表示のnはヘリックス1回転あたりのアミノ酸残基数、mは[[水素結合]]で閉環した構造の[[水素]]原子を含む構成原子数を表している。αヘリックスをこの表記で書くと3.6<sub>13</sub>ヘリックスとなる。 |
||
右巻き3<sub>10</sub>ヘリックスは、p=6. |
右巻き3<sub>10</sub>ヘリックスは、p=6.0 Åで、二面角はラマチャンドランダイアグラムでは禁制領域に入り、側鎖にも立体障害がある。このため、3<sub>10</sub>ヘリックスはあまり見られることはなく、普通はαヘリックスの終端に1回転だけできる。また、2.2<sub>7</sub>リボンは二面角が完全に禁制領域にあるためタンパク質中には存在しない。[[πヘリックス]](4.4<sub>16</sub>ヘリックス)も二面角が禁制領域にあるため、ヘリックスの途中にたまに見られる程度である。 |
||
== βシート構造 == |
== βシート構造 == |
||
| 78行目: | 162行目: | ||
== 非繰り返し構造 == |
== 非繰り返し構造 == |
||
球状のタンパク質においてヘリックスやシート構造は全体の半分ほどで、それ以外の部分は[[ループ]]と呼ばれるひも状の状態をとる。球状タンパクでは二次構造の間にペプチド鎖が急にターンする場所があり、この部分は[[ターン (生化学)|βターン]](逆ターン)と呼ばれる。βターンにはI型とII型が存在し、両方ともアミノ酸4残基で構成されている。βターンは3残基離れたアミノ酸と水素結合して安定化するが、構造がずれて水素結合できないこともある。また、II型βターンでは2番目のアミノ酸残基の酸素原子が3番目のアミノ酸残基のC<sub>β</sub>と衝突するため、ほとんどの3番目のアミノ酸は[[グリシン]]である。 |
球状のタンパク質においてヘリックスやシート構造は全体の半分ほどで、それ以外の部分は[[ループ]]と呼ばれるひも状の状態をとる。球状タンパクでは二次構造の間にペプチド鎖が急にターンする場所があり、この部分は[[ターン (生化学)|βターン]](逆ターン)と呼ばれる。βターンにはI型とII型が存在し、両方ともアミノ酸4残基で構成されている。βターンは3残基離れたアミノ酸と水素結合して安定化するが、構造がずれて水素結合できないこともある。また、II型βターンでは2番目のアミノ酸残基の酸素原子が3番目のアミノ酸残基のC<sub>β</sub>と衝突するため、ほとんどの3番目のアミノ酸は[[グリシン]]である。 |
||
== 脚注 == |
|||
{{reflist}} |
|||
== 参考文献 == |
== 参考文献 == |
||
| 89行目: | 176行目: | ||
* [[確率文脈自由文法]] |
* [[確率文脈自由文法]] |
||
* [[DSSP (水素結合推定アルゴリズム)]] |
* [[DSSP (水素結合推定アルゴリズム)]] |
||
* [[STRIDE]] |
|||
{{二次構造}} |
{{二次構造}} |
||
{{生体分子構造}} |
|||
{{DEFAULTSORT:にしこうそう}} |
{{DEFAULTSORT:にしこうそう}} |
||
2022年12月22日 (木) 08:53時点における最新版


二次構造(にじこうぞう、英: Secondary structure)は、タンパク質や核酸といった生体高分子の主鎖の部分的な立体構造のことである。本項ではタンパク質の二次構造を扱う。
タンパク質の二次構造は、タンパク質の「局所区分」の3次元構造である。最も一般的な2種類の二次構造要素はαヘリックスとβシートであるが、βターンやωループも見られる。二次構造要素は通常、タンパク質が三次構造へと折り畳まれる前の中間状態として自発的に形成される。
二次構造はペプチド主鎖中のアミド水素原子とカルボニル酸素原子との間の水素結合のパターンによって形式的に定義される。二次構造は別法として、正しい水素結合を持っているかどうかにかかわらず、ラマチャンドラン・プロットの特定の領域における主鎖の二面角の規則的なパターンに基づいて定義することもできる。
二次構造の概念は1952年にスタンフォード大学のカイ・ウルリク・リンデルストロム=ラングによって初めて発表された[1][2]。核酸といったその他の生体高分子も特徴的な二次構造を有する。
種類
[編集]| 幾何配置の特性 | αヘリックス | 310ヘリックス | πヘリックス |
|---|---|---|---|
| 回転毎の残基 | 3.6 | 3.0 | 4.4 |
| 残基毎の並進 | 1.5 Å (0.15 nm) | 2.0 Å (0.20 nm) | 1.1 Å (0.11 nm) |
| らせんの半径 | 2.3 Å (0.23 nm) | 1.9 Å (0.19 nm) | 2.8 Å (0.28 nm) |
| 間隔幅 | 5.4 Å (0.54 nm) | 6.0 Å (0.60 nm) | 4.8 Å (0.48 nm) |
最も一般的な二次構造はαヘリックスとβシートである。310ヘリックスおよびπヘリックスといったその他のらせんはエネルギー的に好ましい水素結合パターンを持つと計算されるが、ヘリックスの中心における不利な主鎖の詰め込みのためαヘリックスの末端を除いては天然のタンパク質ではめったに見られない。ポリプロリンヘリックスおよびαシートといったその他の伸長構造は天然状態のタンパク質では希であるが、タンパク質の折り畳みの重要な中間体としてしばしば仮定されている。締まったターンと緩く柔軟なループはより「常連」の二次構造要素を繋ぐ。ランダムコイルは真の二次構造ではないが、正規の二次構造の欠如を示すコンホメーションの一分類である。
アミノ酸は様々な二次構造要素を構成する能力にそれぞれ違いがある。プロリンおよびグリシンはαヘリックス主鎖の規則性を混乱させるため「ヘリックスブレイカー」と呼ばれることがある。しかしながら、どちらのアミノ酸も特有の立体配座能を有しており、ターン中でよく見られる。タンパク質中でらせん配座を取りやすいアミノ酸には、メチオニン、アラニン、ロイシン、グルタミン、リシンがある(アミノ酸の1文字表記で "MALEK")。対照的に、大きな芳香族残基(トリプトファン、チロシン、フェニルアラニン)およびCβ-分岐アミノ酸(イソロイシン、バリン、スレオニン)はβ鎖配座を取りやすい。しかしながら、これらの傾向は、配列のみから二次構造を予測する信頼性のある手法を確立できるほど強いわけではない。
低周波集団振動はタンパク質内の局部剛性に敏感であると考えられており、β構造はα構造あるいは不規則タンパク質よりも一般的に剛直であることが明らかにされている[4][5]。中性子散乱測定は~1 THzのスペクトル特性をβバレルタンパク質GFPの二次構造の集団運動を直接的に結び付けた[6]。
二次構造中の水素結合パターンは大きくゆがんでおり、これが二次構造の自動的な決定を困難にしている。タンパク質二次構造を形式的に決定する手法はいくつか存在する(例: DSSP[7]、DEFINE[8]、STRIDE[9]、ScrewFit[10]、SST[11][12])。
DSSP分類
[編集]
The Dictionary of Protein Secondary Structure(略称DSSP)は、一文字表記を使ってタンパク質二次構造を記述するために一般的に用いられている。二次構造は1951年(タンパク質構造が実験的に決定されるよりも前)にポーリングらによって提唱された水素結合パターンに基づいて割り当てられる。DSSPが定義する8種類の二次構造は以下の通りである。
- G = 3-ターンヘリックス(310ヘリックス)。最小長は3残基。
- H = 4-ターンヘリックス(αヘリックス)。最小長は4残基。
- I = 5-ターンヘリックス(πヘリックス)。最小長は5残基。
- T = 水素結合したターン(3、4、5ターン)
- E = 平行あるいは逆平行βシート配座の伸長鎖。最小長は2残基。
- B = 孤立したβブリッジ(単一ペアのβシート性水素結合形成)残基
- S = ベンド(唯一、水素結合に基づかない割り当て)
- C = コイル(上記のいずれにも該当しない残基)
「コイル」はしばしば ' '(空白)、C (coil)、または '–'(ダッシュ)と表記される。ヘリックス(G、H、I)およびシート配座は全て妥当な長さを持つことを必要とする。これは、タンパク質構造中の2つの隣接した残基同じ水素結合パターンを形成しなければならないことを意味する。ヘリックス性またはシート性水素結合パターンが短かすぎる場合は、それぞれTまたはBと指定される。その他にも二次構造のカテゴリーは存在するが(鋭いターン、ωループ等)、めったに使われない。
二次構造は水素結合によって定義されるため、水素結合の厳密な定義が決定的に重要な意味を持つ。二次構造に関する標準的な水素結合の定義はDSSPの定義であり、これは純粋に静電的なモデルである。DSSPはカルボニル炭素と酸素にそれぞれ±q1 ≈ 0.42eの電荷を、アミド水素と窒素にそれぞれ±q2 ≈ 0.20eの電荷を割り当てる。静電エネルギーは
である。
DSSPによれば、Eが−0.5 kcal/mol (−2.1 kJ/mol) より小さい時かつその時に限り水素結合が存在する。DSSPの式は「物理的」水素結合エネルギーの比較的粗い近似であるものの、二次構造を定義する道具として一般的に受け入れられている。
実験的決定
[編集]生体高分子の大まかな二次構造含量(例えば、「このタンパク質は40%のαヘリックスと20%のβシートを含む」)は分光法により推定することができる[13]。タンパク質に対しては、遠紫外(170–250 nm)円偏光二色性スペクトル測定が一般的な手法である。208および222 nmにおける目立った二重極小はαヘリックス構造を示すのに対して、204 nmまたは217 nmにおける単一極小はランダムコイルまたはβシート構造をそれぞれ反映している。水素結合によるアミド基の結合振動における違いを検出する手法である赤外分光法も用いられるがあまり一般的ではない。二次構造含量はNMRスペクトルの化学シフトを使って正確に推定することができる[14]。
予測
[編集]アミノ酸配列のみからタンパク質三次構造を予測することは非常に困難な問題であるが、より単純な二次構造の定義を用いることはより扱いやすい。
初期の二次構造予測の手法では3つの主要な状態、ヘリックス、シート、またはランダムコイルを予測することしかできなかった。これらの手法は個々のアミノ酸のヘリックスまたはシートを形成する傾向に基づいており、二次構造要素形成の自由エネルギーを推定するための規則を組み合わせられることもあった。このような手法が残基が3つの状態(ヘリックス/シート/コイル)のどれを取るかの予測精度は概して~60%であった。アミノ酸配列から二次構造を予測するために最初に広く用いられた手法はシュー–ファスマン法であった[15][16][17]。
精度の著しい上昇(~80%近くまで)は多重配列アラインメントを利用することによって成された。進化を通じてある位置(とその周辺、典型的には前後に~7残基)に存在するアミノ酸の完全な分布を知ることにより、その位置周辺の構造的傾向についてはるかに良い予想を立てることが可能になった[18][19]。
例えば、あるタンパク質がある位置にグリシンを持つとすると、それ自体はその位置にランダムコイルが存在することを示唆する。しかし、多重配列アラインメントにより、数十億年近くの進化を経ている相同タンパク質の95%においてヘリックスに多く含まれるアミノ酸がその位置(と近傍)に存在することを明らかにするかもしれない。さらに、その位置と近傍における平均疎水性を調べることによって、同じアラインメントがαヘリックスと一致した残基の溶媒接触可能表面積のパターンをも示唆するかもしれない。これらの事実は元のタンパク質のグリシンがランダムコイルではなくαヘリックス構造に含まれることを示唆する。ニューラルネットワーク、隠れマルコフモデル、サポートベクターマシンを含む数種類の手法が、利用可能な全データを組み合わせ上記の3種の二次構造を予測するために用いられている。現代的な予測手法は、全ての位置における予測に対する信頼性スコアも提供する。
二次構造予測手法は継続的に基準に従って評価された(例: EVA)。これらの試験に基づいた最も正確な手法は、PSIPRED、SAM[20]、PORTER[21]、PROF[22]、SABLE[23]であった。改善のための根本的な領域はβ鎖の予測と考えられている。β鎖と確信を持って予測される残基についての精度は高いが、これらの手法は一部のβ鎖領域を見落としがちである(偽陰性)。PDB構造に対して二次構造クラス(ヘリックス/ストランド/コイル)を割り当てる標準手法(DSSPで割り当てられ、この二次構造に対する予測精度が評価される)の特異性のため、全体の予測精度には~90%の上限がありそうである[24]。
最も単純なホモロジーモデリングの場合を除いて、正確な二次構造予測は三次構造の予測において鍵となる要素である。例えば、明確に予測された6つの二次構造要素のパターンβαββαβはフェレドキシン折り畳み構造の特徴である[25]。
応用
[編集]タンパク質および核酸二次構造のどちらも多重配列アラインメントに利用でき、単純な配列情報に加えて二次構造の情報を含めることでより正確にアラインすることできる。RNAでは、塩基対が配列よりもかなり高度に保存されているためあまり役に立たない。一次構造がアラインできないほどに異なるタンパク質間の関係が二次構造の比較によって見出されることがある[18]。
天然タンパク質において、αヘリックスはβストランドよりも安定で、変異に対して頑強で、設計可能であることが示されてきたことから[26]、全てがα-ヘリックスによって構成されている機能性タンパク質の設計はヘリックスとストランドの両方を持つタンパク質の設計よりも容易であると思われており、最近実験的に確かめられている[27]。
ペプチド結合の構造
[編集]

1930-40年代、ライナス・ポーリングとロバート・コリーはポリペプチド鎖内においてアミノ酸やペプチド結合がどのような形状をしているのかを調べるためX線構造解析を行い、右図のような平面構造を取っていることを突き止めた。ペプチドのC-N結合はCα-N結合より0.13 Å短く、C=O結合がアルデヒドやケトンのC=Oよりも0.02 Å短い事から次のように共鳴していると考えられている。

ペプチド結合の共鳴エネルギーは平面のとき最大値(約85 kJ/mol)をとり、平面から90° ねじれると共鳴エネルギーはゼロとなることからも平面構造が非常に強いことが分かる。ペプチド結合は普通トランス型をとり、隣接するCα同士は点対称の関係になる。シス型をとった場合、立体障害のためトランス型より約8 kJ/molだけ不安定になる。しかし、プロリンの手前のペプチドでは少しだけ安定化する。このためプロリンの手前のペプチドの約10%はシス型をとっている。
ポリペプチド主鎖の二面角
[編集]ポリペプチド鎖は平面構造のペプチド結合が繋がっている。したがって、ポリペプチドの構造はそのペプチド結合面同士の二面角(ねじれ角)で表すことができ、Cα-N結合角はφ、Cα-C結合角はψで、それぞれの角度はCαから見て時計回りに回ると値が大きくなると決めている。二面角とφ、そしてψは立体障害のために様々な制約を受ける。
ラマチャンドランダイアグラム
[編集]
ラマチャンドランダイアグラム、ラマチャンドランプロット、またはラマチャンドランマップとは、φ、ψ値、各原子間距離の計算によって立体的に許容されるペプチドの構造の範囲を図示したものである。
| 二次構造 | φ(°) | ψ(°) |
|---|---|---|
| 右巻きαヘリックス | -57 | -47 |
| 平行β構造 | -119 | 113 |
| 逆平行β構造 | -139 | 135 |
| 右巻き310ヘリックス | -49 | -26 |
| 右巻きπヘリックス | -57 | -70 |
| 2.27リボン | -78 | 59 |
| 左巻きポリグリシンII、ポリ-L-プロリンIIヘリックス | -79 | 150 |
| コラーゲン | -51 | 153 |
| 左巻きαヘリックス | 57 | 47 |
ラマチャンドランダイアグラムの示す構造可能範囲は各アミノ酸の側鎖の大きさによって変化する。例えばグリシンはCβが無いため他のアミノ酸に比べて許容範囲はずっと広い。また、プロリンの側鎖は環状であるため許容範囲は極端に制限される(φ = −60°±25°)。
ヘリックス構造
[編集]ポリペプチド鎖の各Cα炭素が同じようにねじれるとヘリックス(螺旋)構造をとる。ヘリックス構造はφ、ψではなく、1回転あたりの残基数(n:右巻きは正、左巻きは負)、1回転で軸方向に進む距離(ピッチ、p)で表される。p=0のとき閉環となり、p=2のときは平面リボン構造をとる。
αヘリックス
[編集]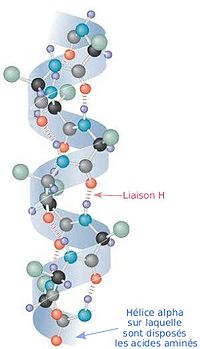
ポリペプチドのヘリックス構造の中で二面角と水素結合形成の双方を満足する構造はαヘリックスだけで、L-アミノ酸で作られるαヘリックスはφ=−57°、ψ=−47°、n=3.6、p=5.4 Åである。αヘリックスではすべてのN-H基が4残基離れたアミノ酸のC=O基へ水素結合をしている。このときのN…O間の距離は2.8 Åで、水素結合には適当であり、会合エネルギーも最大となる。右巻き構造では側鎖は外側を向いており主鎖にとっても相互にも障害にならない。しかし左巻き構造では側鎖が主鎖に近すぎるため作られることは少ない。
その他のヘリックス構造
[編集]2.27リボン、310ヘリックスのようなnmという表示のnはヘリックス1回転あたりのアミノ酸残基数、mは水素結合で閉環した構造の水素原子を含む構成原子数を表している。αヘリックスをこの表記で書くと3.613ヘリックスとなる。
右巻き310ヘリックスは、p=6.0 Åで、二面角はラマチャンドランダイアグラムでは禁制領域に入り、側鎖にも立体障害がある。このため、310ヘリックスはあまり見られることはなく、普通はαヘリックスの終端に1回転だけできる。また、2.27リボンは二面角が完全に禁制領域にあるためタンパク質中には存在しない。πヘリックス(4.416ヘリックス)も二面角が禁制領域にあるため、ヘリックスの途中にたまに見られる程度である。
βシート構造
[編集]βシートは、φとψが同じ角度で繰り返し、水素結合が2本のポリペプチド鎖の間にある構造である。βシートには平行βシートと逆平行βシートがある。水素結合が適切にできるためには完全な平面構造(φ=180°=ψ)ではなく襞(プリーツ)状をとる。襞の周期は7.0Åである。
非繰り返し構造
[編集]球状のタンパク質においてヘリックスやシート構造は全体の半分ほどで、それ以外の部分はループと呼ばれるひも状の状態をとる。球状タンパクでは二次構造の間にペプチド鎖が急にターンする場所があり、この部分はβターン(逆ターン)と呼ばれる。βターンにはI型とII型が存在し、両方ともアミノ酸4残基で構成されている。βターンは3残基離れたアミノ酸と水素結合して安定化するが、構造がずれて水素結合できないこともある。また、II型βターンでは2番目のアミノ酸残基の酸素原子が3番目のアミノ酸残基のCβと衝突するため、ほとんどの3番目のアミノ酸はグリシンである。
脚注
[編集]- ^ Linderstrøm-Lang KU (1952). Lane Medical Lectures: Proteins and Enzymes. Stanford University Press. pp. 115. ASIN B0007J31SC
- ^ “Kaj Ulrik Linderstrøm-Lang (1896–1959)”. Protein Sci. 6 (5): 1092–100. (1997). doi:10.1002/pro.5560060516. PMC 2143695. PMID 9144781. "He had already introduced the concepts of the primary, secondary, and tertiary structure of proteins in the third Lane Lecture (Linderstram-Lang, 1952)"
- ^ Steven Bottomley (2004年). “Interactive Protein Structure Tutorial”. January 9, 2011閲覧。
- ^ “Secondary structure and rigidity in model proteins”. Soft Matter 9 (40): 9548–56. (October 2013). doi:10.1039/C3SM50807B. PMID 26029761.
- ^ “Rigidity, secondary structure, and the universality of the boson peak in proteins”. Biophysical Journal 106 (12): 2667–74. (June 2014). doi:10.1016/j.bpj.2014.05.009. PMC 4070067. PMID 24940784.
- ^ “Coherent neutron scattering and collective dynamics in the protein, GFP”. Biophys. J. 105 (9): 2182–87. (2013). doi:10.1016/j.bpj.2013.09.029. PMC 3824694. PMID 24209864.
- ^ “Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features”. Biopolymers 22 (12): 2577–637. (Dec 1983). doi:10.1002/bip.360221211. PMID 6667333.
- ^ “Identification of structural motifs from protein coordinate data: secondary structure and first-level supersecondary structure”. Proteins 3 (2): 71–84. (1988). doi:10.1002/prot.340030202. PMID 3399495.
- ^ “Knowledge-based protein secondary structure assignment”. Proteins 23 (4): 566–79. (Dec 1995). doi:10.1002/prot.340230412. PMID 8749853.
- ^ Calligari, Paolo A.; Kneller, Gerald R. (2012-12-01). “ScrewFit: combining localization and description of protein secondary structure” (英語). Acta Crystallographica Section D 68 (12): 1690–1693. doi:10.1107/s0907444912039029. ISSN 0907-4449.
- ^ Arun Konagurthu. “SST: Protein Secondary structural assignment using Minimum Message Length inference”. Laboratory of Computational Biology, Monash University. 2018年1月4日閲覧。
- ^ “Minimum message length inference of secondary structure from protein coordinate data”. Bioinformatics 28 (12): i97–i105. (Jun 2012). doi:10.1093/bioinformatics/bts223. PMC 3371855. PMID 22689785.
- ^ “Spectroscopic methods for analysis of protein secondary structure”. Anal. Biochem. 277 (2): 167–76. (2000). doi:10.1006/abio.1999.4320. PMID 10625503.
- ^ “Rapid protein fold determination using unassigned NMR data”. Proc. Natl. Acad. Sci. U.S.A. 100 (26): 15404–09. (2003). doi:10.1073/pnas.2434121100. PMC 307580. PMID 14668443.
- ^ “Prediction of protein conformation”. Biochemistry 13 (2): 222–45. (Jan 1974). doi:10.1021/bi00699a002. PMID 4358940.
- ^ “Empirical predictions of protein conformation”. Annu. Rev. Biochem. 47: 251–76. (1978). doi:10.1146/annurev.bi.47.070178.001343. PMID 354496.
- ^ “Prediction of the secondary structure of proteins from their amino acid sequence”. Adv. Enzymol. Relat. Areas Mol. Biol. 47: 45–148. (1978). doi:10.1002/9780470122921.ch2. PMID 364941.
- ^ a b “Integrating protein secondary structure prediction and multiple sequence alignment”. Current Protein & Peptide Science 5 (4): 249–66. (Aug 2004). doi:10.2174/1389203043379675. PMID 15320732.
- ^ “Protein secondary structure prediction”. Methods Mol. Biol. 609: 327–48. (2010). doi:10.1007/978-1-60327-241-4_19. PMID 20221928.
- ^ “SAM-T08, HMM-based protein structure prediction”. Nucleic Acids Res. 37 (Web Server issue): W492–97. (2009). doi:10.1093/nar/gkp403. PMC 2703928. PMID 19483096.
- ^ “Porter: a new, accurate server for protein secondary structure prediction”. Bioinformatics 21 (8): 1719–20. (2005). doi:10.1093/bioinformatics/bti203. PMID 15585524.
- ^ “PredictProtein—an open resource for online prediction of protein structural and functional features”. Nucleic Acids Res. 42 (Web Server issue): W337–43. (2014). doi:10.1093/nar/gku366. PMC 4086098. PMID 24799431.
- ^ “Combining prediction of secondary structure and solvent accessibility in proteins”. Proteins 59 (3): 467–75. (2005). doi:10.1002/prot.20441. PMID 15768403.
- ^ “The effect of long-range interactions on the secondary structure formation of proteins”. Protein Science 14 (8): 1955–963. (Aug 2005). doi:10.1110/ps.051479505. PMC 2279307. PMID 15987894.
- ^ “Structural classification of thioredoxin-like fold proteins”. Proteins 58 (2): 376–88. (2005). doi:10.1002/prot.20329. PMID 15558583. "Since the fold definition should include only the core secondary structural elements that are present in the majority of homologs, we define the thioredoxin-like fold as a two-layer / sandwich with the βαββαβ secondary-structure pattern."
- ^ “Alpha helices are more robust to mutations than beta strands”. PLoS Computational Biology 12 (12): 1–16. (2016). doi:10.1371/journal.pcbi.1005242. PMID 27935949.
- ^ “Global analysis of protein folding using massively parallel design, synthesis, and testing”. Science 357 (6347): 168–175. (2017). doi:10.1126/science.aan0693. PMID 28706065.
参考文献
[編集]- 『ヴォート生化学 第3版』 DONALDO VOET・JUDITH G.VOET 田宮信雄他訳 東京化学同人 2005.2.28

