ピタゴラスの定理

レオナルド・ダ・ヴィンチによるピタゴラスの定理の証明。橙色のついた部分を 90 度回転し、緑色の部分は裏返して橙色に重ねる。

視覚的証明

初等幾何学におけるピタゴラスの定理（ピタゴラスのていり、英: Pythagorean theorem）は、直角三角形の3辺の長さの関係を表す。斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は

$c^{2}=a^{2}+b^{2}$

が成り立つという等式の形で述べられる。三平方の定理（さんへいほうのていり）、勾股弦の定理（こうこげんのていり）とも呼ばれる。

ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。例えば、直交座標系において原点と任意の点を結ぶ線分の長さは、ピタゴラスの定理に従って、その点の座標成分を2乗したものの総和の平方根として表すことができる。このことは2次元の座標系に限らず、3次元の系やより大きな次元の系についても成り立つ。この事実から、ピタゴラスの定理を用いて任意の2点の間の距離を測ることができる。このようにして導入される距離はユークリッド距離と呼ばれる。

「ピタゴラスが直角二等辺三角形のタイルが敷き詰められた床を見ていて、この定理を思いついた」など幾つかの逸話が知られているものの、この定理はピタゴラスが発見したかどうかは分からない。バビロニア数学のプリンプトン322や古代エジプトなどでもピタゴラス数については知られていたが、彼らが定理を発見していたかどうかは定かではない。

中国古代の数学書『九章算術』や『周髀算経』でもこの定理が取り上げられている。中国ではこの定理を勾股定理、商高定理等と呼び、日本の和算でも中国での名称を用いて鉤股弦の法（こうこげんのほう）等と呼んだ。三平方の定理という名称は、敵性語が禁じられていた第二次世界大戦中に文部省の図書監修官であった塩野直道の依頼を受けて、数学者末綱恕一が命名したものである。

ピタゴラス数

a² + b² = c² を満たす自然数の組 (a, b, c) をピタゴラス数またはピタゴラスの三つ組数 (Pythagorean triple) という。特に、a, b, c が互いに素であるピタゴラス数 (a, b, c) を原始的 (primitive) あるいは素 (prime) であるといい、そのようなピタゴラス数は原始ピタゴラス数 (primitive Pythagorean triple) などと呼ばれる。全てのピタゴラス数は、原始ピタゴラス数の正の整数倍により得られる。

ピタゴラス数 (a, b, c) が原始的であるためには、3つのうち2つが互いに素であることが必要十分である。

ピタゴラス数の性質

2つの整数mとn(m＞n≧1)を基にピタゴラス数(a,b,c)を生成できることを示した図。単一の黄色の長方形および正方形の面積はいずれも$m^{2}n^{2}$となっている。

色付きの正方形群で三辺の長さが整数の直角三角形を表した例。正方形の合計数は図中右上のように1つの長方形内に余白なく収まるものとなっている。

ピタゴラス数を面積及び長さの比で表した図。青は$m^{2}-n^{2}$、緑は$2mn$、赤は$m^{2}+n^{2}$を表現している。右上の矢印の先で青の長方形の右の辺の延長線並びに赤と青の円弧が交差していることで、面積及び長さの比が直角三角形の三辺の比として成り立っていることが確認できる。

数1に相当する長さを定めた上でピタゴラス数の関係を長さで表した図。ピタゴラス数を表現する長さが直角三角形(桃色)の三辺として成り立っていることが確認できる。(赤矢印が示す交点一致)

自然数の組 (a, b, c) が原始ピタゴラス数であるためには、ある自然数 m, n が

• m と n は互いに素
• m > n
• m − n は奇数

を満たすとして、

(a, b, c) = (m² − n², 2mn, m² + n²) or (2mn, m² − n², m² + n²)

であることが必要十分である。上記の (m, n) は無数に存在し、2mn は重複しないから、原始ピタゴラス数は無数に存在する。これにより、すべての原始ピタゴラス数を重複なく見つけ出すことができる。

例えば

(m, n) = (2, 1) のとき (a, b, c) = (3, 4, 5)

(m, n) = (3, 2) のとき (a, b, c) = (5, 12, 13)

(m, n) = (4, 1) のとき (a, b, c) = (8, 15, 17)

である。

原始ピタゴラス数 (a, b, c) について、次のような性質も成り立つ。

• a または b は 4 の倍数
• a または b は 3 の倍数
• a または b または c は 5 の倍数

また、一般のピタゴラス数 (a, b, c) に対して、S = 1/2ab（直角三角形の面積）は平方数でない。

直角三角形の三辺の長さを整数とするための調整

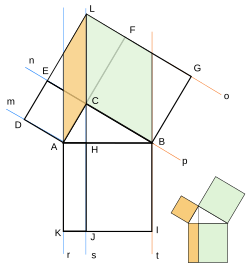
直角三角形の三辺の長さを整数とするための調整の図

直角三角形の三辺の長さを整数とするための調整の図において、赤の正方形の面積から青の正方形の面積を差し引いた残りの面積を互いに合同な黄の長方形4枚で占めている。

黄の長方形の長辺と短辺の長さが整数であれば、

• 赤の正方形の辺の長さは黄の長方形の長辺と短辺の和
• 青の正方形の辺の長さは黄の長方形の長辺と短辺の差

となり、いずれも整数として表せることになる。

また、黄の長方形の面積を整数の二乗で表せれば、黄の長方形4枚分の面積に等しい緑の正方形の辺の長さも整数で表すことができる。

なおかつ、二つの正方形（緑と青）の面積の和が別の正方形（赤）の面積となることにもなり、この場合、三つの正方形の各辺の長さを用いて直角三角形(桃色)を作れることになる。

ただし、黄の長方形は当然正方形となってはならず（長辺と短辺の差によって青の正方形を作る必要がある）、互いに異なりながらその積が整数の二乗となる2つの数を黄の長方形の幅と高さに割り当てる必要がある。

それを実現する方法の一つとして、黄の長方形の幅と高さをそれぞれ異なる整数の二乗とする方法がある。

図では、数1の長さを定めた上で整数m,n(m＞n≧1)の長さも設定し、それぞれの二乗を黄の長方形の辺の長さにしている。

（緑の正方形の辺の長さは $4m^{2}n^{2}$ の正の平方根 $2mn$ となる。）

青、緑、赤の各正方形の辺の長さをa,b,cとすると、

• $a=m^{2}-n^{2}$
• $b=2mn$
• $c=m^{2}+n^{2}$

となり、それぞれ整数であり、$a^{2}+b^{2}=c^{2}$ が成り立つので、a,b,cを三辺の長さとする三角形(桃色)は直角三角形となる。

Jesmanowicz 予想

1956年に Jesmanowicz が以下の予想を提出した。

(a, b, c) を原始ピタゴラス数、n を自然数とする。x, y, z が

$(an)^{x}+(bn)^{y}=(cn)^{z}$

で自然数解を持つには、

$x=y=z=2$

であることが必要である。

一般化

角の一般化

→詳細は「余弦定理」を参照

第二余弦定理

c² = a² + b² − 2ab cos C

はピタゴラスの定理を C = π/2 = 90° → cos C = 0 の場合として含む。 つまり、第二余弦定理はピタゴラスの定理を一般の角度について拡張した定理になっている。

指数の一般化

→詳細は「フェルマーの最終定理」を参照

指数の 2 の部分を一般化すると

aⁿ + bⁿ = cⁿ

となる。n = 2 の場合は自明でない（つまり a, b, c のいずれも 0 でない）整数解は実質原始ピタゴラス数であり、無数に存在するが、n ≥ 3 の場合には自明でない整数解は存在しない（詳細はフェルマーの最終定理を参照）。

次元の一般化

→詳細は「en:De Gua's theorem」を参照

3次元空間内に平面があるとき、その閉領域 S の面積は、yz 平面、zx 平面、xy 平面への射影の面積 S_x, S_y, S_z を用いて

$S^{2}={S_{x}}^{2}+{S_{y}}^{2}+{S_{z}}^{2}$

と表される。これは高次元へ一般化できる。

ピタゴラスの定理の証明

この定理には数百通りもの異なる証明が知られている。ここにいくつかの代表的な証明を挙げる。

以下では頂点 A, B, C からなる三角形を △ABC と表す。また、各辺 AB, BC, CA に向かい合う角をそれぞれ ∠C, ∠A, ∠B と表し、各頂点 A, B, C の対辺 BC, CA, AB の長さをそれぞれ a, b, c と表す。 頂点の記号は直角三角形 △ABC の直角が ∠C になるように与える。

相似による証明

相似を用いた証明

頂点 C から斜辺 AB に下ろした垂線の足を H とする。△ABC, △ACH, △CBH は互いに相似である。よって △ABC と △ACH の相似比より

${\text{AC}}:{\text{AH}}={\text{AB}}:{\text{AC}}\Longrightarrow {\text{AH}}={{\text{AC}}\times {\text{AC}} \over {\text{AB}}}={b^{2} \over c}$

であり、同様に △ABC と △CBH の相似比より

${\text{BH}}={a^{2} \over c}$

である。したがって

$c={\text{AB}}={\text{AH}}+{\text{BH}}={b^{2} \over c}+{a^{2} \over c}$

であるから、両辺に$c$ を掛けて

$c^{2}=a^{2}+b^{2}$

を得る。

正方形を用いた証明

正方形を用いた証明

△ABC と合同な4個の三角形を図のように並べると、外側に一辺が a + b の正方形（以下「大正方形」）が、内側に一辺が c の正方形（以下「小正方形」）ができる。

（大正方形の面積）=（小正方形の面積）+（直角三角形の面積）× 4

である。大正方形の面積は (a + b)², 小正方形の面積は c², 直角三角形4個の面積の合計は

${ab \over 2}\times 4=2ab$

である。これらを代入すると、

$(a+b)^{2}=c^{2}+2ab$

整理して

$a^{2}+b^{2}=c^{2}$

を得る。

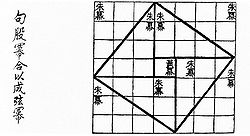
幾何学的な証明

『周髀算経』におけるピタゴラスの定理の証明（中国語: 句股冪合以成弦冪）

内接円を用いた証明

△ABC の面積 S は

$S={\frac {ab}{2}}$

(1)

である。また △ABC の内接円の半径を r とすると

$c=(a-r)+(b-r)$

であり、これを半径 r について解くと

$r={\frac {a+b-c}{2}}$

(2)

となる。一方、三角形の面積 S を内接円の半径 r を用いて表すと

$S={r(a+b+c) \over 2}$

(3)

となる。(3) に (1), (2) を代入すると

${ab \over 2}={(a+b-c)(a+b+c) \over 4}$

となり、整理すると

$a^{2}+b^{2}=c^{2}$

が得られる。

オイラーの公式を用いた証明

三角関数と指数関数は冪級数によって定義されているものとする。（指数法則やオイラーの公式の証明に本定理が使用されない定義であればよい。）まず sin² θ + cos² θ = 1 が任意の複素数 θ に対して成り立つことを（3通りの方法で）示す。

オイラーの公式より

${\begin{aligned}1&=e^{0}=e^{i\theta -i\theta }=e^{i\theta }e^{-i\theta }\\&=(\cos \theta +i\sin \theta )(\cos \theta -i\sin \theta )\\&=\sin ^{2}\theta +\cos ^{2}\theta \end{aligned}}$

または

${\begin{aligned}\sin ^{2}\theta +\cos ^{2}\theta &=\left({\frac {e^{i\theta }-e^{-i\theta }}{2i}}\right)^{2}+\left({\frac {e^{i\theta }+e^{-i\theta }}{2}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }-2}{-4}}+{\frac {e^{2i\theta }+e^{-2i\theta }+2}{4}}\\&={\frac {4}{4}}=1\end{aligned}}$

もしくは、オイラーの公式から三角関数の半角の公式を導出する。

${\begin{aligned}\sin ^{2}\theta &=\left({\frac {e^{i\theta }-e^{-i\theta }}{2i}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }-2}{-4}}\\&={\frac {1-\cos 2\theta }{2}}\ ,\\\cos ^{2}\theta &=\left({\frac {e^{i\theta }+e^{-i\theta }}{2}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }+2}{4}}\\&={\frac {1+\cos 2\theta }{2}}\ .\end{aligned}}$

$\therefore \sin ^{2}\theta +\cos ^{2}\theta =1.$

(1)

(1) の式はピタゴラスの基本三角関数公式 (Fundamental Pythagorean trigonometric identity) と呼ばれている。

(1) の時点ですでに単位円上において本定理の成立が明らかである。なぜならば、本定理の逆は本定理を用いずに証明可能であるし、単位円上の任意の点の座標は (cosθ, sinθ) で表せるからである。

さて、前提とした △ABC について考え、∠A = θ とおけば

$a=c\cdot \sin \theta$

$b=c\cdot \cos \theta$

したがって

$a^{2}=c^{2}\sin ^{2}\theta$

(2)

$b^{2}=c^{2}\cos ^{2}\theta$

(3)

(2), (3) より

$a^{2}+b^{2}=c^{2}(\sin ^{2}\theta +\cos ^{2}\theta )$

(4)

(1), (4) より

$a^{2}+b^{2}=c^{2}$

が得られる。

三角関数の微分公式を用いた証明

正弦および余弦関数を微分すれば

$(\sin \theta )'=\cos \theta$

(1)

$(\cos \theta )'=-\sin \theta$

(2)

(1), (2) および微分公式より

$(\sin ^{2}\theta +\cos ^{2}\theta )'=2\sin \theta \cos \theta +2\cos \theta (-\sin \theta )=0$

したがって

$\sin ^{2}\theta +\cos ^{2}\theta =C$

ここで C は定数である。θ = 0 を代入すると sin 0 = 0, cos 0 = 1 であるので、C = 1 が得られる。よって

$\sin ^{2}\theta +\cos ^{2}\theta =1$

(3)

が得られる。 ここで、前提とした △ABC について考え、∠A = θ とおいて、(3) および、三角関数と直角三角形の関係を考慮すれば

$a^{2}+b^{2}={a^{2}+b^{2} \over 1}={a^{2}+b^{2} \over \sin ^{2}\theta +\cos ^{2}\theta }={a^{2}+b^{2} \over {a^{2}+b^{2} \over c^{2}}}=c^{2}$

が得られる。

三角関数の不定積分を用いた証明

下記のように関数を定める。

${\begin{aligned}f(\theta )=\sin ^{2}\theta +\cos ^{2}\theta .\end{aligned}}$

上記を漸化式を利用して不定積分すると

${\begin{aligned}\int f(\theta )d\theta &=\int (\sin ^{2}\theta )d\theta +\int (\cos ^{2}\theta )d\theta \\&=\left({1 \over 2}\theta -{1 \over 2}\sin \theta \cos \theta +C_{1}\right)+\left({1 \over 2}\theta +{1 \over 2}\sin \theta \cos \theta +C_{2}\right)\\&=\theta +C_{1}+C_{2}\end{aligned}}$

である。微分積分学の基本定理を考慮し、これを微分すると

${\begin{aligned}{\frac {d}{d\theta }}\left\{\int f(\theta )d\theta \right\}&=f(\theta )&={\frac {d}{d\theta }}(\theta +C_{1}+C_{2})&=1\end{aligned}}$

である。したがって

${\begin{aligned}f(\theta )=\sin ^{2}\theta +\cos ^{2}\theta &=1.\end{aligned}}$

ゆえに、ピタゴラスの定理は成立する。

三角関数の加法定理を用いた証明

三角関数は級数など（幾何以外の原理）によって定義されているものとし、オイラーの公式など（証明に本定理を使用しない方法）によって導出された三角関数の加法定理を用いれば

$1=\cos 0=\cos(\theta -\theta )=\cos \theta \cos \theta +\sin \theta \sin \theta =\cos ^{2}\theta +\sin ^{2}\theta$

または

$\sin ^{2}\theta +\cos ^{2}\theta =\sin \theta \cos \left({\frac {\pi }{2}}-\theta \right)+\cos \theta \sin \left({\frac {\pi }{2}}-\theta \right)=\sin {\frac {\pi }{2}}=1$

が得られる。 また、加法定理を応用した三角関数の積和公式を用いて

${\begin{aligned}\sin ^{2}\theta &={\frac {\cos(\theta -\theta )-\cos(\theta +\theta )}{2}}\\&={\frac {1-\cos 2\theta }{2}}\end{aligned}}$

${\begin{aligned}\cos ^{2}\theta &={\frac {\cos(\theta -\theta )+\cos(\theta +\theta )}{2}}\\&={\frac {1+\cos 2\theta }{2}}\end{aligned}}$

したがって

$\sin ^{2}\theta +\cos ^{2}\theta =1$

が得られる。 両辺に c ² を乗算して

$c^{2}\sin ^{2}\theta +c^{2}\cos ^{2}\theta =c^{2}$

ここで、前提とした △ABC について考え、∠A = θ とおいて、三角関数と直角三角形の関係を考慮すれば

$c^{2}\times \left({a \over c}\right)^{2}+c^{2}\times \left({b \over c}\right)^{2}=c^{2}$

よって

$a^{2}+b^{2}=c^{2}$

が得られる。

冪級数展開を用いた証明

三角関数は級数によって定義されているものとし、cosθ と sinθ の自乗をそれぞれ計算すると

${\begin{aligned}\sin ^{2}\theta &=\left(\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}\theta ^{2n+1}\right)^{2}\\&=\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {(-1)^{k}}{(2k+1)!}}{\frac {(-1)^{n-k}}{(2n-2k+1)!}}\theta ^{2n+2}\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}\theta ^{2n+2}}{(2n+2)!}}\sum _{k=0}^{n}{\binom {2(n+1)}{2k+1}}\\&=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n-1}{\binom {2n}{2k+1}}\\&=-\sum _{n=1}^{\infty }{\frac {(-1)^{n}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n-1}{\binom {2n}{2k+1}}\\\cos ^{2}\theta &=\left(\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}\theta ^{2n}\right)^{2}\\&=\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {(-1)^{k}}{(2k)!}}{\frac {(-1)^{n-k}}{(2n-2k)!}}\theta ^{2n}\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n}{\binom {2n}{2k}}\\&=1+\sum _{n=1}^{\infty }{\frac {(-1)^{n}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n}{\binom {2n}{2k}}\end{aligned}}$

となる。ここで二項定理より

${\begin{aligned}\sum _{k=0}^{n}{\binom {2n}{2k}}-\sum _{k=0}^{n-1}{\binom {2n}{2k+1}}&=\sum _{m=0}^{2n}(-1)^{m}{2n \choose m}&=(1-1)^{2n}&=0\end{aligned}}$

である。したがって

$\sin ^{2}\theta +\cos ^{2}\theta =1$

が得られる。 ここで、前提とした △ABC について考え、∠A = θ とおいて、三角関数と直角三角形の関係を考慮し、各辺の比を考えれば

$\sin ^{2}\theta :\cos ^{2}\theta :1=a^{2}:b^{2}:c^{2}$

であるから

$a^{2}+b^{2}=c^{2}$

が得られる。

回転行列を用いた証明

平面の原点を中心とする角 θ の回転は

$R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}$

で表される。 R (θ) R (−θ) = I₂ （単位行列）であるが、この式の左辺を直接計算すると

${\begin{aligned}R(\theta )\cdot R(-\theta )&={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \end{bmatrix}}\\&={\begin{bmatrix}\cos ^{2}\theta +\sin ^{2}\theta &\cos \theta \sin \theta -\sin \theta \cos \theta \\\sin \theta \cos \theta -\cos \theta \sin \theta &\sin ^{2}\theta +\cos ^{2}\theta \end{bmatrix}}\\&={\begin{bmatrix}\sin ^{2}\theta +\cos ^{2}\theta &0\\0&\sin ^{2}\theta +\cos ^{2}\theta \end{bmatrix}}\end{aligned}}$

となる。したがって

$\sin ^{2}\theta +\cos ^{2}\theta =1$

が得られる。 ここで、前提とした △ABC について考え、∠A = θ とおいて、三角関数と直角三角形の関係を考慮すれば、正弦定理より

${\begin{aligned}{\frac {a}{\sin \theta }}&={\frac {b}{\sin(\pi -{\frac {\pi }{2}}-\theta )}}={\frac {c}{\sin({\frac {\pi }{2}})}}\\{\frac {a}{\sin \theta }}&={\frac {b}{\cos \theta }}=c\end{aligned}}$

であるから

$a^{2}+b^{2}=c^{2}$

が得られる。

三角関数と双曲線関数を用いた証明

任意の z ∈ C に対し

${\begin{aligned}\sin ^{2}iz+\cos ^{2}iz&=(i\sinh z)^{2}+\cosh ^{2}z\\&=\cosh ^{2}z-\sinh ^{2}z\\&=1\end{aligned}}$

である。よって任意の θ ∈ C に対して

$\sin ^{2}\theta +\cos ^{2}\theta =1$

が成り立つ。 ここで、前提とした △ABC について考え、∠A = θ とおいて、三角関数と直角三角形の関係を考慮すれば、連比関係より

${\frac {a^{2}}{\sin ^{2}\theta }}={\frac {b^{2}}{\cos ^{2}\theta }}=c^{2}$

であるから

$a^{2}+b^{2}=c^{2}$

が得られる。

ピタゴラスの定理の逆の証明

ピタゴラスの定理の逆とは、△ABC に対して

$a^{2}+b^{2}=c^{2}$

が成立すれば、△ABC は ∠C = π/2 の直角三角形であるというものである。以下に証明を示す。

ピタゴラスの定理に依存しない証明

ピタゴラスの定理に依存しない証明

a ² + b ² = c ² を満たす △ABC において、線分 AB を b ² : a ² の比に内分する点を D とすると

${\begin{aligned}{\text{AD}}&=c\times {\frac {b^{2}}{b^{2}+a^{2}}}\\&=c\times {\frac {b^{2}}{c^{2}}}\\&={\frac {b^{2}}{c}}\\{\text{DB}}&=c\times {\frac {a^{2}}{b^{2}+a^{2}}}\\&=c\times {\frac {a^{2}}{c^{2}}}\\&={\frac {a^{2}}{c}}\end{aligned}}$

である。これより、△ABC と △ACD において

${\begin{aligned}{\text{AB}}:{\text{AC}}&=c:b\\{\text{AC}}:{\text{AD}}&=b:{\frac {b^{2}}{c}}=c:b\end{aligned}}$

であるから

${\text{AB}}:{\text{AC}}={\text{AC}}:{\text{AD}}$

が成り立つ。ここで

$\angle {\text{BAC}}=\angle {\text{CAD}}$

であるから、2辺比夾角相等より

$\triangle {\text{ABC}}\sim \triangle {\text{ACD}}$

が成り立つ。したがって

$\angle {\text{ACB}}=\angle {\text{ADC}}$

である。 同様に △ABC と △CBD において

${\begin{aligned}{\text{AB}}:{\text{BC}}&=c:a\\{\text{CB}}:{\text{BD}}&=a:{\frac {a^{2}}{c}}=c:a\end{aligned}}$

であるから

${\text{AB}}:{\text{BC}}={\text{CB}}:{\text{BD}}$

が成り立つ。ここで

$\angle {\text{ABC}}=\angle {\text{CBD}}$

であるから、2辺比夾角相等より

$\triangle {\text{ABC}}\sim \triangle {\text{CBD}}$

が成り立つ。したがって

$\angle {\text{ACB}}=\angle {\text{CDB}}$

である。ここで

$\angle {\text{ADC}}+\angle {\text{CDB}}=\pi$

であるから

$\angle {\text{ACB}}+\angle {\text{ACB}}=2\angle {\text{ACB}}=\pi$

である。したがって

$\angle {\text{ACB}}={\frac {\pi }{2}}$

である。ゆえに、△ABC は ∠C = π/2 の直角三角形である。

同一法を用いた証明

ピタゴラスの定理を用いた証明

B'C' = a, A'C' = b，∠C' = π/2 である直角三角形 A'B'C' において、A'B' = c' とすれば、ピタゴラスの定理より

$a^{2}+b^{2}=c'\,^{2}$

(1)

が成り立つ。 一方、仮定から △ABC において

$a^{2}+b^{2}=c^{2}$

(2)

が成り立っている。(1) 、(2) より

$c^{2}=c'\,^{2}$

c > 0, c' > 0 より

$c=c'$

したがって、3辺相等から

$\triangle {\text{ABC}}\equiv \triangle {\text{A'B'C'}}$

よって、∠C = ∠C' = π/2 である。 ゆえに、△ABC は ∠C = π/2 の直角三角形である。

対偶を用いた証明

△ABC において ∠C ≠ π/2 であると仮定する。頂点 A から直線 BC に下した垂線の足を D とし、AD = h, CD = d とする。

∠C < π/2 の場合、直角三角形 ABD においてピタゴラスの定理より

${\begin{aligned}c^{2}&=(a-d)^{2}+h^{2}\\&=a^{2}-2ad+d^{2}+h^{2}\end{aligned}}$

であり、同様に直角三角形 ACD では

$b^{2}=d^{2}+h^{2}$

である。よって

$c^{2}=a^{2}-2ad+b^{2}<a^{2}+b^{2}$

となる。

∠C > π/2 の場合も同様に考えて

${\begin{aligned}c^{2}&=(a+d)^{2}+h^{2}\\&=a^{2}+2ad+d^{2}+h^{2}\\&=a^{2}+2ad+b^{2}\end{aligned}}$

ゆえに

$c^{2}>a^{2}+b^{2}$

となる。

よっていずれの場合も

$a^{2}+b^{2}\neq c^{2}$

である。対偶を取って、a ² + b ² = c ² ならば ∠C = π/2 である。

なお、この証明から分かるように、

• ∠C < π/2 ⇔ a ² + b ² > c ²
• ∠C = π/2 ⇔ a ² + b ² = c ²
• ∠C > π/2 ⇔ a ² + b ² < c ²

という対応がある。

余弦定理を用いた証明

余弦定理を用いた証明

ピタゴラスの定理は既に証明されているとする。△ABC において、a = BC, b = CA, c = AB, C = ∠ACB とおくと、余弦定理より

$c^{2}=a^{2}+b^{2}-2ab\cos C$

である。仮定より

$a^{2}+b^{2}=c^{2}$

であるから

$\cos C=0$

である。三角形の内角の和は π であるから、0 < C < π である。 したがって

$\angle {\text{ACB}}=\cos ^{-1}0={\frac {\pi }{2}}$

である。ゆえに、△ABC は ∠C = π/2 の直角三角形である。

ベクトルを用いた証明

ピタゴラスの定理は既に証明されているとする。△ABC において

$\Vert {\vec {c}}\|^{2}=\Vert {\vec {a}}\|^{2}+\Vert {\vec {b}}\|^{2}$

であり

${\vec {c}}={\vec {b}}-{\vec {a}}$

である。 ここで

${\begin{aligned}\Vert {\vec {c}}\|^{2}&={\vec {c}}\cdot {\vec {c}}\\&=({\vec {b}}-{\vec {a}})\cdot ({\vec {b}}-{\vec {a}})\\&=\Vert {\vec {b}}\|^{2}-2{\vec {b}}\cdot {\vec {a}}+\Vert {\vec {a}}\|^{2}\\\end{aligned}}$

である。したがって

${\vec {b}}\cdot {\vec {a}}=0$

である。よって

$\angle {\text{C}}={\frac {\pi }{2}}$

である。ゆえに、ピタゴラスの定理の逆が証明された。

三角関数と逆三角関数を用いた証明

△ABC において、それぞれの辺の長さを AB = c, BC = a, CA = b と表し、a ² + b ² = c ² 、a , b , c > 0、a , b , c < ∞ を満たすものとする。 ピタゴラスの定理は既知とする。 三角関数と逆三角関数を無限級数で定義する。 θ を角度とし、0 <θ < π/2 とする。 オイラーの公式などの幾何以外の原理による証明より e^iθ e^−iθ = sin² θ + cos² θ = 1 であり、θ ∈ R ⇒ sin θ , cos θ ∈ R である。 仮定の式を ( a/c ) ² + ( b/c ) ² = 1 と整理し、複素数の極形式との整合性も考慮して

${\begin{aligned}\sin \theta &={\frac {a}{c}}&={\frac {a}{\sqrt {a^{2}+b^{2}}}}\end{aligned}}$

${\begin{aligned}\cos \theta &={\frac {b}{c}}&={\frac {b}{\sqrt {a^{2}+b^{2}}}}\end{aligned}}$

とおく。

次に、R の区間 [ g , h ] で定義され、C の値をとる関数 z (t) = x (t) +iy (t) が微分可能で z ' (t) が連続のとき、z (t) によって定義される曲線 C の長さ l を

$l=\int _{g}^{h}|z'(t)|\,dt=\int _{g}^{h}{\sqrt {z'(t){\bar {z'(t)}}}}\,dt=\int _{g}^{h}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\,dt$

として天下り的に定義する。単位円上の円弧は

$z(t)=e^{it}=\cos t+i\sin t\ (0\leq t\leq \theta )$

なる関数で与えられる。この円弧の長さは

$l=\int _{0}^{\theta }{\sqrt {(-\sin t)^{2}+(\cos t)^{2}}}\,dt=\int _{0}^{\theta }\,dt=\theta$

である。角度の絶対値を角の大きさと呼ぶ。しからば、原点を頂点とする角の大きさとは、その角が切りとる単位円の円弧の長さということになる。このように、角の大きさは単位円上における円弧の長さで表される。 任意の点 p ∈ C を中心とする半径 1 の円上の円弧は

$z(t)=p+e^{it}\ (0\leq t\leq \theta )$

なる関数で与えられるため、この円弧の長さも単位円上の円弧の長さと同様にして求められる。したがって、三角形の内角にも、この定義を適用できる。

ところで

${\begin{aligned}x^{2}+y^{2}\leq 1\end{aligned}}$

の場合の2つの角の大きさの和は

${\begin{aligned}\sin ^{-1}x+\sin ^{-1}y=\sin ^{-1}(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}})\end{aligned}}$

である。ただし、ここで議論する逆三角関数は主値を考える。ここで

${\begin{aligned}x^{2}+y^{2}=1\end{aligned}}$

の時は

${\begin{aligned}\sin ^{-1}x+\sin ^{-1}y&=\sin ^{-1}1&={\frac {\pi }{2}}\end{aligned}}$

である。 したがって、2つの角の大きさの和は

${\begin{aligned}\sin ^{-1}{\frac {a}{c}}+\sin ^{-1}{\frac {b}{c}}&={\frac {\pi }{2}}\end{aligned}}$

である。また、逆三角関数の定義と公式より

${\begin{aligned}\sin ^{-1}(\sin \theta )&=\theta ,\\\sin ^{-1}(\cos \theta )&={\frac {\pi }{2}}-\cos ^{-1}(\cos \theta )\\&={\frac {\pi }{2}}-\theta \end{aligned}}$

である。なぜならば、f (x) = sin⁻¹ x とおくと

$f(x)=\sin ^{-1}x=\int {\frac {1}{\sqrt {1-x^{2}}}}dx=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {x^{2n+1}}{2n+1}}+C$

f (0) = 0 より、C = 0 であるから

$\sin ^{-1}x=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {x^{2n+1}}{2n+1}}$

である。 次に f (y) = cos⁻¹ y とおくと

${\begin{aligned}f(y)&=\cos ^{-1}y&=-\int {\frac {1}{\sqrt {1-y^{2}}}}dy&=-\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {y^{2n+1}}{2n+1}}+C\end{aligned}}$

余弦による円周率の定義 cos π/2 = 0 より、f (0) = π/2 となり、C = π/2 であるから

${\begin{aligned}\cos ^{-1}y&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {y^{2n+1}}{2n+1}}\\&={\frac {\pi }{2}}-\sin ^{-1}y\end{aligned}}$

である。したがって

${\begin{aligned}\sin ^{-1}y&={\frac {\pi }{2}}-\cos ^{-1}y\end{aligned}}$

である。 ゆえに、三角形の角

${\begin{aligned}\sin ^{-1}{\frac {a}{c}}=\sin ^{-1}(\sin \theta )=\theta \end{aligned}}$

および

${\begin{aligned}\sin ^{-1}{\frac {b}{c}}=\sin ^{-1}(\cos \theta )={\frac {\pi }{2}}-\theta \end{aligned}}$

は、余角の関係にある。 仮定より、△ABC の辺 a , b , c には、内分点も外分点もなく、辺 a , b , c 以外の線分、半直線、直線や曲線もない。 また、a : b : c の三角形（仮定の三角形）と a/c : b/c : 1の三角形（正弦と余弦関数の定義からみた三角形） は、三辺比相等より相似であるから、対応する角の大きさは各々等しい。ここで、仮定の三角形 △ABC と正弦と余弦関数の定義からみた三角形は相似であるから、それらの三角形の内角のうち2角の大きさはsin⁻¹ a/c と sin⁻¹ b/c である。（ここでは、先述の2つの角が仮定の三角形のどれかの内角の大きさと等しいことを証明できればよいだけなので、仮に対応する角がどれか分からなくても良い。後述する最後の議論によってsin⁻¹ a/c の大小関係は、辺 a の対角 A の角度の大小関係に対応し、sin⁻¹ b/c の大小関係は、辺 b の対角 B の角度の大小関係に対応することが分かる。） すなわち、θ や π/2 − θ は、それぞれ △ABC の内角である。 複素数平面上の異なる3点 α, β, γ が頂点を α とする $\angle$βαγ をなすとき、この角の大きさは複素数の商 γ−α/β−α の偏角の大きさである。記号arg の計算規則から arg γ−α/β−α + arg α−β/γ−β + arg β−γ/α−γ = arg γ−α/β−α⋅ α−β/γ−β⋅ β−γ/α−γ = arg (−1) = π である。前述と平行線公準より内角の和は π であり、三角形の6要素より三角形の内角は3つであるから、余角の関係にある2つの角を除く、残りの1つの角の大きさは π/2 である。 0 <θ < π/2 であるため、△ABC の最も大きい内角は π/2 である。 仮定より、最も長い辺は max {a , b , c} = c であり、三角形の辺と角の大小関係（大きい辺に向かい合う角は、小さい辺に向かい合う角より大きい。）から、その対角は C = π/2 である。 ゆえに、△ABC は C = π/2 の直角三角形である。 さらに議論を進めると

${\begin{aligned}\sin ^{-1}(\cos \theta )&={\frac {\pi }{2}}-\cos ^{-1}(\cos \theta )\\&={\frac {\pi }{2}}-\theta ,\end{aligned}}$

${\begin{aligned}\sin ^{-1}\left\{\sin \left({\frac {\pi }{2}}-\theta \right)\right\}&={\frac {\pi }{2}}-\theta \end{aligned}}$

であるから、鋭角 θ の余角の正弦は、角 θ の余弦である。 さらに

${\begin{aligned}\cos ^{-1}(\sin \theta )&={\frac {\pi }{2}}-\sin ^{-1}(\sin \theta )\\&={\frac {\pi }{2}}-\theta ,\\\end{aligned}}$

${\begin{aligned}\cos ^{-1}\left\{\cos \left({\frac {\pi }{2}}-\theta \right)\right\}&={\frac {\pi }{2}}-\theta \end{aligned}}$

であるから、鋭角 θ の余角の余弦は、角 θ の正弦である。

三角関数と逆三角関数を用いた証明

ここで、θ が 0 から π/2 まで増加するとき、sin θ = a/c は、0 から 1 まで狭義単調増加し、cos θ = b/c は、1 から 0 まで狭義単調減少する。 前述の議論との整合性を保つためには、辺 a の対角を A = θ とおかなければならない。 さらに、残りの辺 b , c の対角を B , C とおくと

$\tan A+\tan B+\tan C=\tan A\cdot \tan B\cdot \tan C\,$

となる。 ゆえに

${\begin{aligned}A&=\sin ^{-1}{\frac {a}{c}}=\sin ^{-1}(\sin \theta )=\theta ,\\B&=\sin ^{-1}{\frac {b}{c}}=\sin ^{-1}(\cos \theta )=\sin ^{-1}\left\{\sin \left({\frac {\pi }{2}}-\theta \right)\right\}={\frac {\pi }{2}}-\theta ,\\C&=\pi -(A+B)={\frac {\pi }{2}}\end{aligned}}$

となる。

参考文献

• 出光, 英則 著、銀林浩編 編『ピタゴラスがくれたおくり物 ピタゴラスの定理』国土社〈数学ワンダーランド 7〉、1997年8月。ISBN 4-337-56207-9。http://www.kokudosha.co.jp/search/info.php?isbn=9784337562073。 
• カプラン, ロバート、カプラン, エレン『数学の隠れたハーモニー ピタゴラスの定理のすべて』水谷淳訳、ソフトバンククリエイティブ、2011年12月。ISBN 978-4-7973-6467-5。http://www.sbcr.jp/products/4797364675.html。  — 原題：Hidden harmonies.
• シルヴァーマン, ジョセフ・H『はじめての数論 発見と証明の大航海 ピタゴラスの定理から楕円曲線まで』鈴木治郎訳（原著第3版）、ピアソン・エデュケーション、2007年4月。ISBN 978-4-89471-492-2。  — 原題：A friendly introduction to number theory (3rd ed.).
• マオール, エリ『ピタゴラスの定理 4000年の歴史』伊理由美訳、岩波書店、2008年2月。ISBN 978-4-00-005878-0。http://www.iwanami.co.jp/.BOOKS/00/9/0058780.html。  — 原題：The Pythagorean theorem.
• 森下, 四郎『ピタゴラスの定理100の証明法 幾何の散歩道』（改訂版）プレアデス出版、2010年8月。ISBN 978-4-903814-36-0。 
• 森下, 四郎『ピタゴラスの定理をめぐる2つの謎 三平方の定理の謎』プレアデス出版、2010年12月。ISBN 978-4-903814-39-1。 

関連項目

• 計量テンソル
• プリンプトン322
• ユークリッド原論

外部リンク

• 百科事典マイペディア『ピタゴラスの定理』 - コトバンク
• Weisstein, Eric W. "Pythagorean Theorem". mathworld.wolfram.com (英語).