定積過程 (ていせきかてい、英 : isochoric process )とは、系 の体積 を一定に保ちながら、系をある状態から別の状態へと変化させる熱力学 過程のことである。等容変化ともいう。準静的過程 とは限らない。例えば、燃焼熱 を測定する際にボンベ熱量計 の中で起こる過程は、不可逆 な定積過程である。容積一定の容器の中で起こる熱力学過程は、定積過程として解析できることが多い。例えば、容積一定の容器に入れた気体 や液体 を温めたり冷やしたりする過程は、典型的な定積過程である。このような過程でも準静的過程には限らない。過程の途中で容器内の温度や圧力が不均一であってもよいし、過冷却 や過飽和 などが起こっていてもよい。
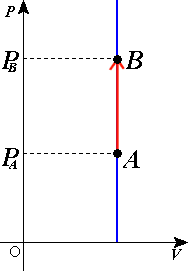
閉じた系 の体積 V を一定に保ちながら、ある平衡状態Aから別の平衡状態Bに移行させる定積過程について考える。
系の体積が一定に保たれるので、系の体積変化に伴う仕事 はない。よって、電気的仕事などのその他の仕事もないときには、熱力学第一法則 により、定積過程の内部エネルギー 変化 ΔU は系が外部から得た熱 Q に等しい。
Δ
U
=
Q
{\displaystyle \Delta U=Q}
エンタルピー H の変化は H = U + PV より
Δ
H
=
Q
+
V
Δ
P
{\displaystyle \Delta H=Q+V\Delta P}
となる。ただし ΔP は過程に伴う系の圧力変化
Δ
P
=
P
B
−
P
A
{\displaystyle \Delta P=P_{\text{B}}-P_{\text{A}}}
である。
内部エネルギー U と容器の容積 V により系の状態を一意に指定できる場合には、系の温度 T を (U,V) の関数として
T
=
T
(
U
,
V
)
{\displaystyle T=T(U,V)}
と表すことができる。T(U,V) の関数形は容器の中にある物質の量と種類で決まる。
一般には、内部エネルギー U と容器の容積 V だけで系の状態を一意に指定できるとは限らない。例えば、燃焼などの化学反応が容積一定の断熱 容器の中で起こった場合は ΔU = Q = 0 であるが、容器内の温度は変化する。よってこの場合は、系の温度 T を (U,V) の関数として表すことはできない。以下では断りのない限り、 系の状態が (U,V) により一意に定まる場合について述べる。
内部エネルギーが U で体積が V のときの系の温度を T(U,V) とするならエントロピー S の変化は
Δ
S
=
∫
U
A
U
B
d
U
T
(
U
,
V
)
{\displaystyle \Delta S=\int _{U_{\text{A}}}^{U_{\text{B}}}{\frac {dU}{T(U,V)}}}
である。なぜなら、系の温度が T(U,V) のとき、環境の温度 Tex を Tex = T(U,V) + δT と設定して系に熱量 d'Q を与えるなら、 温度差 δT が十分に小さいときにこの過程は準静的微小変化になり、さらに定積過程であれば dU = d'Q なので、エントロピーの定義により
d
S
=
d
′
Q
T
ex
=
d
U
T
(
U
,
V
)
{\displaystyle dS={\frac {d'Q}{T_{\text{ex}}}}={\frac {dU}{T(U,V)}}}
となるからである。
ヘルムホルツエネルギー F の変化は、F = U - TS の関係を使って
Δ
F
=
Δ
(
U
−
T
S
)
=
Q
−
T
B
Δ
S
−
S
A
Δ
T
{\displaystyle \Delta F=\Delta (U-TS)=Q-T_{\text{B}}\Delta S-S_{\text{A}}\Delta T}
となる。
ギブズエネルギー G の変化は、G = F + PV の関係を使って
Δ
G
=
Δ
F
+
V
Δ
P
{\displaystyle \Delta G=\Delta F+V\Delta P}
となる。
以上より、体積 V が一定の過程における U, H, S, F, G の変化量は、系が外部から得た熱 Q と過程に伴う系の圧力変化 ΔP と始状態のエントロピー SA と 関数 T(U, V) から求められることが分かる。
等温過程 では ΔT = 0 であるので、定積等温過程では U, H, S, F, G の変化量は、以下の式で与えられる。
Δ
U
=
Q
{\displaystyle \Delta U=Q}
Δ
H
=
Q
+
V
Δ
P
{\displaystyle \Delta H=Q+V\Delta P}
Δ
S
=
Q
T
A
{\displaystyle \Delta S={\frac {Q}{T_{\text{A}}}}}
Δ
F
=
Q
−
T
B
Q
T
A
=
0
{\displaystyle \Delta F=Q-T_{\text{B}}{\frac {Q}{T_{\text{A}}}}=0}
Δ
G
=
V
Δ
P
{\displaystyle \Delta G=V\Delta P}
定積等温過程ではヘルムホルツエネルギー F は変化しない。
適当な量の純物質 が封入された密閉容器を加熱することで、定積等温過程を実現することができる。すなわち、固相と気相の二相共存の状態にある系を加熱していくと、純物質の量が適当な量であれば三重点 に達して、固相と気相と液相の三相共存状態になる。液相が現れてから固相が消えるまでは、定積等温過程である。三重点で加えられた熱量の分だけ系の内部エネルギーは増加するが、三相が共存している間はヘルムホルツエネルギーは変化しない。
系の状態は (U, V) の関数として表すよりも、(T, V) の関数として表したほうが実用上は便利である。 純物質の三重点のように (T, V) だけでは系の状態が一意に定まらない場合もあるが、ここでは始状態が (TA , V) で、終状態が (TB , V) でそれぞれ一意に定まる場合について述べる。
一般に、系の温度 T(U, V) は 有限個の点を除いて U で偏微分可能であり
(
∂
T
∂
U
)
V
≥
0
{\displaystyle \left({\frac {\partial T}{\partial U}}\right)_{V}\geq 0}
である。 (∂T/∂U)V > 0 となる範囲と (∂T/∂U)V = 0 となる範囲を分けて考えれば、定積過程では内部エネルギー U の変化は
Δ
U
=
∫
U
A
U
B
d
U
=
∫
T
A
T
B
(
∂
U
∂
T
)
V
d
T
+
∑
i
Δ
i
U
(
T
i
,
V
)
{\displaystyle \Delta U=\int _{U_{\text{A}}}^{U_{\text{B}}}dU=\int _{T_{\text{A}}}^{T_{\text{B}}}\left({\frac {\partial U}{\partial T}}\right)_{V}dT+\sum _{i}\Delta _{i}U(T_{i},V)}
となる。ここで最右辺の第二項の和は、TA とTB の間にある、(∂T/∂U)V = 0 となる温度 T についてとる。温度 Ti は TA から TB まで準静的に変化させたときに定積等温過程となる i 番目の温度であり、Δi U(Ti , V) はその等温過程で外界から吸収する熱 Q である。
エントロピー S の変化も同様に考えると
Δ
S
=
∫
U
A
U
B
d
U
T
(
U
,
V
)
=
∫
T
A
T
B
1
T
(
∂
U
∂
T
)
V
d
T
+
∑
i
Δ
i
U
(
T
i
,
V
)
T
i
{\displaystyle \Delta S=\int _{U_{\text{A}}}^{U_{\text{B}}}{\frac {dU}{T(U,V)}}=\int _{T_{\text{A}}}^{T_{\text{B}}}{\frac {1}{T}}\left({\frac {\partial U}{\partial T}}\right)_{V}dT+\sum _{i}{\frac {\Delta _{i}U(T_{i},V)}{T_{i}}}}
となる。
系の定積熱容量 を
C
V
(
T
,
V
)
=
(
∂
U
∂
T
)
V
{\displaystyle C_{V}(T,V)=\left({\frac {\partial U}{\partial T}}\right)_{V}}
で定義すると U と S の変化はそれぞれ
Δ
U
=
∫
T
A
T
B
C
V
(
T
,
V
)
d
T
+
∑
i
Δ
i
U
(
T
i
,
V
)
{\displaystyle \Delta U=\int _{T_{\text{A}}}^{T_{\text{B}}}C_{V}(T,V)dT+\sum _{i}\Delta _{i}U(T_{i},V)}
Δ
S
=
∫
T
A
T
B
C
V
(
T
,
V
)
T
d
T
+
∑
i
Δ
i
U
(
T
i
,
V
)
T
i
{\displaystyle \Delta S=\int _{T_{\text{A}}}^{T_{\text{B}}}{\frac {C_{V}(T,V)}{T}}dT+\sum _{i}{\frac {\Delta _{i}U(T_{i},V)}{T_{i}}}}
と表される。また (T, V) の関数として S が一意に定まる温度範囲で
Δ
S
=
∫
T
A
T
B
(
∂
S
∂
T
)
V
d
T
{\displaystyle \Delta S=\int _{T_{\text{A}}}^{T_{\text{B}}}\left({\frac {\partial S}{\partial T}}\right)_{V}dT}
であることから
(
∂
S
∂
T
)
V
=
C
V
(
T
,
V
)
T
{\displaystyle \left({\frac {\partial S}{\partial T}}\right)_{V}={\frac {C_{V}(T,V)}{T}}}
が成り立つ。
ヘルムホルツエネルギー F の変化は、定積等温過程では ΔF = 0 なので
Δ
F
=
Δ
U
−
T
B
Δ
S
−
S
A
Δ
T
=
∫
T
A
T
B
(
T
−
T
B
)
(
∂
S
∂
T
)
V
d
T
−
S
A
Δ
T
=
−
∫
T
A
T
B
S
(
T
,
V
)
d
T
{\displaystyle \Delta F=\Delta U-T_{\text{B}}\Delta S-S_{\text{A}}\Delta T=\int _{T_{\text{A}}}^{T_{\text{B}}}(T-T_{\text{B}})\left({\frac {\partial S}{\partial T}}\right)_{V}dT-S_{\text{A}}\Delta T=-\int _{T_{\text{A}}}^{T_{\text{B}}}S(T,V)dT}
となる。また
Δ
F
=
∫
T
A
T
B
(
∂
F
∂
T
)
V
d
T
{\displaystyle \Delta F=\int _{T_{\text{A}}}^{T_{\text{B}}}\left({\frac {\partial F}{\partial T}}\right)_{V}dT}
であることから
(
∂
F
∂
T
)
V
=
−
S
(
T
,
V
)
{\displaystyle \left({\frac {\partial F}{\partial T}}\right)_{V}=-S(T,V)}
が成り立つ。
エンタルピー H とギブズエネルギー G の変化はそれぞれ
Δ
H
=
Δ
U
+
V
Δ
P
{\displaystyle \Delta H=\Delta U+V\Delta P}
Δ
G
=
Δ
F
+
V
Δ
P
{\displaystyle \Delta G=\Delta F+V\Delta P}
である。
以上より、体積 V が一定の過程における U, S, F, H, G の変化量は、系の定積熱容量 CV (T, V) と過程に伴う系の圧力変化 ΔP と始状態のエントロピー SA と CV (T, V) が発散する温度 Ti における内部エネルギーの跳び Δi U(Ti , V) から求められることが分かる。
容積 V の容器に入った物質量 n の理想気体 を状態Aから状態Bに移行させる定積過程について考える。理想気体の定積モル熱容量 CV,m は体積 V に依らない。簡単のため、ここでは CV,m が温度 T にも依らない定数とする。
内部エネルギー U とエントロピー S の変化はそれぞれ
Δ
U
=
∫
T
A
T
B
n
C
V
,
m
d
T
=
n
C
V
,
m
Δ
T
{\displaystyle \Delta U=\int _{T_{\text{A}}}^{T_{\text{B}}}nC_{V,{\text{m}}}dT=nC_{V,{\text{m}}}\Delta T}
Δ
S
=
∫
T
A
T
B
n
C
V
,
m
T
d
T
=
n
C
V
,
m
ln
T
B
T
A
{\displaystyle \Delta S=\int _{T_{\text{A}}}^{T_{\text{B}}}{\frac {nC_{V,{\text{m}}}}{T}}dT=nC_{V,{\text{m}}}\ln {\frac {T_{\text{B}}}{T_{\text{A}}}}}
である。
ヘルムホルツエネルギー F の変化は
Δ
F
=
Δ
U
−
T
B
Δ
S
−
S
A
Δ
T
=
n
(
C
V
,
m
−
S
m
(
T
A
,
V
m
)
)
Δ
T
−
n
C
V
,
m
T
B
ln
T
B
T
A
{\displaystyle \Delta F=\Delta U-T_{\text{B}}\Delta S-S_{\text{A}}\Delta T=n\left(C_{V,{\text{m}}}-S_{\text{m}}(T_{\text{A}},V_{\text{m}})\right)\Delta T-nC_{V,{\text{m}}}T_{\text{B}}\ln {\frac {T_{\text{B}}}{T_{\text{A}}}}}
となる。ただし Sm (T,Vm ) は、温度 T、モル体積 Vm = V/n におけるこの理想気体のモルエントロピーである。
エンタルピー H の変化は、理想気体の状態方程式 PV = nRT とマイヤーの関係式 CP,m (T) = CV,m (T) + R を使うと
Δ
H
=
Δ
U
+
Δ
(
P
V
)
=
n
(
C
V
,
m
+
R
)
Δ
T
=
n
C
P
,
m
Δ
T
{\displaystyle \Delta H=\Delta U+\Delta (PV)=n(C_{V,{\text{m}}}+R)\Delta T=nC_{P,{\text{m}}}\Delta T}
となる。ギブズエネルギー G の変化も同様に
Δ
G
=
Δ
F
+
Δ
(
P
V
)
=
n
(
C
P
,
m
−
S
m
(
T
A
,
V
m
)
)
Δ
T
−
n
C
V
,
m
T
B
ln
T
B
T
A
{\displaystyle \Delta G=\Delta F+\Delta (PV)=n\left(C_{P,{\text{m}}}-S_{\text{m}}(T_{\text{A}},V_{\text{m}})\right)\Delta T-nC_{V,{\text{m}}}T_{\text{B}}\ln {\frac {T_{\text{B}}}{T_{\text{A}}}}}
となる。
定積過程では、理想気体は外部に仕事 W をしない。
W
=
0
{\displaystyle W=0}
定積過程で理想気体が外部から得る熱 Q は
Q
=
Δ
U
=
n
C
V
,
m
Δ
T
{\displaystyle Q=\Delta U=nC_{V,{\text{m}}}\Delta T}
である。
理想気体 を状態Aから状態Bへと移行させる定積過程を考える。このとき熱力学第一法則 より、
Δ
U
=
Q
−
W
{\displaystyle \Delta U=Q-W}
ただし
Δ
U
{\displaystyle \Delta U}
内部エネルギー の変化、
Q
{\displaystyle Q}
熱量 、
W
{\displaystyle W}
仕事 である。ここで、この過程を無限に分割した微小過程を考えると、その微小過程中に外部にする仕事
d
W
{\displaystyle dW}
d
W
=
F
d
x
=
P
S
d
x
=
P
d
V
{\displaystyle dW=Fdx=PSdx=PdV}
である。ここで
P
{\displaystyle P}
d
V
{\displaystyle dV}
d
V
=
0
{\displaystyle dV=0}
d
W
=
P
d
V
=
0
{\displaystyle dW=PdV=0}
となる。よって、熱力学第一法則の式は、
Δ
U
=
Q
{\displaystyle \Delta U=Q}
と書き直せる。ここで、定積過程における気体の、単位物質量あたりの比熱 を定積モル比熱
c
V
{\displaystyle c_{V}}
Q
=
n
c
V
Δ
T
{\displaystyle Q=nc_{V}\Delta T}
となる。ここでnは理想気体の物質量 、Tは絶対温度 である。
以上のことから気体の内部エネルギーと定積モル比熱について次の関係が成り立つ。
Δ
U
=
n
c
V
Δ
T
{\displaystyle \Delta U=nc_{V}\Delta T}
内部エネルギー の変化量
Δ
U
{\displaystyle \Delta U}
絶対温度 の変化量
Δ
T
{\displaystyle \Delta T}
物理量 なので、この等式は定積過程に限らずあらゆる過程で成り立つ(ただし、
Q
=
n
c
V
Δ
T
{\displaystyle Q=nc_{V}\Delta T}