垂重円
表示
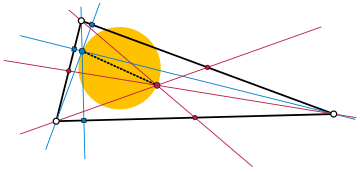

F1,F2: フェルマー点
F: フォイエルバッハ点
I: 内心
G: ジェルゴンヌ点
U: 類似重心
幾何学において垂重円 (すいじゅうえん[1][2][3]、英: orthocentroidal circle)は、正三角形でない三角形に対して定義される、垂心と重心を直径の両端とする円である。
1894年、アンドリュー・ギーナン は、内心が常に垂重円内にあるが、九点円の中心とは一致しない、つまり九点円の中心で穴をあけた垂重円の円板内にあることを示した[4][5][6][7][8]。
更に、第一フェルマー点、ジェルゴンヌ点、類似重心は垂重円の開円板の中にあり、第二フェルマー点とフォイエルバッハ点は外にある[5]。垂心と重心を固定して三角形を動かしたとき、ブロカール点の一方が中へ、もう一方が外にあるような、ブロカール点の軌跡は垂重円の開円板である[9]。
垂重円の直径の二乗は、 である 。ここで a, b, cは三角形の辺の長さで D は外接円の直径である。垂重円はレスター円、ステヴァノヴィッチ円などと直交する。また垂重円の中心、つまり垂心と重心の中点X(381)は三線座標を用いて、以下の式で表される[10]。
出典
[編集]- ^ Eugène Rouché, Charles de Comberousse 著、小倉金之助 編『初等幾何学 第1巻 平面之部』山海堂書店、1913年、613頁。doi:10.11501/930885。
- ^ 長澤龜之助 編『幾何学精義(数学中等参考叢書)』成美堂書店、1907年、763頁。doi:10.11501/828520。
- ^ Eugène Rouché, Charles de Comberousse 著、小倉金之助 訳『初等幾何學 第2卷 空間之部』山海堂書店、1915年、878頁。doi:10.11501/1082037。
- ^ Guinand, Andrew P. (1984), “Euler lines, tritangent centers, and their triangles”, American Mathematical Monthly 91 (5): 290–300, doi:10.2307/2322671, JSTOR 2322671.
- ^ a b Bradley, Christopher J.; Smith, Geoff C. (2006), “The locations of triangle centers”, Forum Geometricorum 6: 57–70.
- ^ Stern, Joseph (2007), “Euler's triangle determination problem”, Forum Geometricorum 7: 1–9.
- ^ Franzsen, William N. (2011), “The distance from the incenter to the Euler line”, Forum Geometricorum 11: 231–236.
- ^ LevershaGerry; SmithG. C.「Euler and triangle geometry」『The Mathematical Gazette』第91巻、第522号、436–452頁、November 2007。doi:10.1017/S0025557200182087。JSTOR 40378417。.
- ^ Bradley, Christopher J.; Smith, Geoff C. (2006), “The locations of the Brocard points”, Forum Geometricorum 6: 71–77.
- ^ “ENCYCLOPEDIA OF TRIANGLE CENTERS X(381) = MIDPOINT OF X(2) AND X(4)”. faculty.evansville.edu. 2024年5月2日閲覧。
外部リンク
[編集]- Weisstein, Eric W. "Orthocentroidal Circle". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Lester Circle". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Stevanović Circle". mathworld.wolfram.com (英語).


