レア・ディザスター
| 経済学 |
|---|
 |
| 理論 |
| ミクロ経済学 マクロ経済学 数理経済学 |
| 実証 |
| 計量経済学 実験経済学 経済史 |
| 応用 |
|
公共 医療 環境 天然資源 農業 開発 国際 都市 空間 地域 地理 労働 教育 人口 人事 産業 法 文化 金融 行動 |
| 一覧 |
|
経済学者 学術雑誌 重要書籍 カテゴリ 索引 概要 |
| 経済 |
|
|
レア・ディザスター(英: rare disaster)とは経済に著しく大きな負の影響を与える、まれな経済学的事象のことである。レア・ディザスターによってエクイティプレミアムパズルや利子率の変動、また他の経済現象を説明することができることから、レア・ディザスターは重要である。
レア・ディザスターとはGDPの大きな下落であり、少なくとも消費が10%下落するようなものである。例として、大恐慌やアジア金融危機等の金融危機、世界大戦や地域紛争などの戦争、インフルエンザやコロナウイルスなどのパンデミックによる疫病の拡大、津波や地震などの自然災害などがある。しかしながら、GDPと消費に大きなインパクトを与えるあらゆる事象がレア・ディザスターとして考えられる。
レア・ディザスターの考え方は1988年に Thomas Rietz によってエクイティプレミアムパズルを説明する方法として提案された[1]。それ以来、レア・ディザスター仮説を補強するような証拠がいくつかの経済学者から提出されているが、依然として多くの経済学者はレア・ディザスター仮説に懐疑的である。
モデル
[編集]ロバート・バローによって発表されたレア・ディザスターモデルは外生的かつ確率的な生産を伴うロバート・ルーカスのツリー型資産価格モデルに基づいている。この経済は閉じていて[2]、ツリー全体は固定されており、生産量は消費に等しく(A t + 1 = C t)、投資や減価償却が存在しないものとなっている。(A t + 1)は経済における全てのツリーの生産量であり、()はその期におけるツリーの価格(つまり株価)である。以下の方程式は一つの期におけるツリーのグロスリターンである[3]。
レア・ディザスターをモデル化するために、バローは以下のような方程式を導入した。この方程式は集計生産量の成長率についての確率過程である。バローのレア・ディザスターモデルにおいては以下の3つの経済的ショックが存在する。
a.) 正規分布に従うIIDなショック。
b.) (): 負債はデフォルトしないが、生産の急激な収縮を伴うディザスター。
c.) (): 少なくとも部分的に負債がデフォルトし、生産の急激な収縮を伴うディザスター。
タイプ ω () はレア・ディザスターであり、()はi.i.d.である確率変数である。これらの変数は独立であり、ゆえに方程式内で交換できる。この時、上の方程式から、レア・ディザスター()によって起こる収縮の程度は以下の方程式で決定される。
この方程式において、p は各期においてレア・ディザスターが起こる確率である。もし、レア・ディザスターが起こったならば、b だけ消費の収縮が起こる。正しくレア・ディザスターをモデル化するためには、p は小さく、b は大きくなければならない。バローの分析において d が負債の部分的なデフォルトの問題を取り扱う為に導入されている。
応用
[編集]Rietz とバロー以来、レア・ディザスターのフレームワークはファイナンスと経済学における多くの事象を説明する為に用いられている。
エクイティプレミアム
[編集]エクイティプレミアムパズルの多くの部分がバローとRietzによって提案されたレア・ディザスターのシナリオにより説明可能である。もし人々がレア・ディザスター(大恐慌や第一次世界大戦、第二次世界大戦など)は起こり得るが、自身の生きている間には起こらないだろうと考えているとするならば、株式のリスクプレミアムは高くなりうるということが基本的な理論である。
バローとそれに続く経済学者たちは、この主張を裏付けるような歴史的証拠を提出してきた。バローは、19世紀中ごろから今日まで世界の経済において大きな規模のレア・ディザスターが十分な頻度で起こっているということを示した。
さらに、長期において多くの国でおよそ5.0%のリスクプレミアムであるということも示されている。しかしながら、特定の期間で見ると、リスクプレミアムは高かったり低かったりするだろう。例えば、大恐慌におけるデータセットが観測されたならば、そのエクイティプレミアムはおよそ0.4%となる。なぜならば、大恐慌はレア・ディザスターだったからである[3]。
無リスク金利の振る舞い
[編集]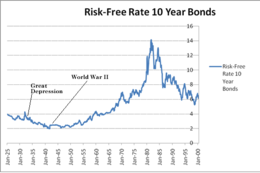
無リスク金利(固定された所得を受け取るような利子、例えば債券)もまたレア・ディザスターによって説明されうる。アメリカのデータを用いた際、生起確率が1.7%であるようなレア・ディザスターをデータセットに導入すると、レア・ディザスターモデルは大きな規模の利子率の下落(12.7%から3.5%)を起こす[3]。
加えて、Rajnish Mehraによる、大恐慌と第二次世界大戦における原爆投下のような事象における無リスク金利の振る舞いに関する批判にバローは反論している。バローは二つの影響が人々のレア・ディザスターについての期待に対して働いていると推論している。核戦争を起こし得る事象(キューバ危機や第二次世界大戦)において、レア・ディザスターの起こる確率は上昇し、ゆえに利子率は低下する。しかしながら政府の債券がデフォルトする可能性もまた上昇する。というのも国家が破壊されるという潜在的な可能性による。よって債券の利率は上昇する。これら二つの力は逆に働き、よって結果としてあいまいな動きとなる。無リスク金利は大恐慌以前はそのままで大恐慌以後に下落し、そして第二次世界大戦の当初においては下落したがその後上昇している[3]。
歴史
[編集]エクイティプレミアムパズルはエドワード・プレスコットとRajnish Mehraによって1985年に初めて示された。1988年、Rietz は大きく稀な経済的ショックがエクイティプレミアムの説明となり得ると提案した[1]。しかしながら、そんなことは不可能だと当時は思われた。というのもそのような出来事は稀すぎて現実には起こりえないように思われたからである[4]。レア・ディザスターの理論は2005年まで忘れ去られていたが、バローが19世紀と20世紀の世界中の国家から証拠を見出し、そのようなレア・ディザスターは起こり得るし、起こってきたことを示した。バローの論文以降、他の経済現象に対するレア・ディザスターのインパクトについての多様なアイデアが様々な研究者により提出された[4]。しかしながら、レア・ディザスターが実際にどの程度エクイティリスクプレミアムを説明するかについて懐疑的な研究者は多く、Mehraは依然としてレア・ディザスター理論の妥当性について疑念を表明している[4]。
論争
[編集]Rajnish Mehra はレア・ディザスターがエクイティプレミアムパズルや実質金利の挙動を説明するというRietz の主張に懐疑的であった。というのもRietzが特定したレア・ディザスターはアメリカにおいて起こっていなかったからである。Rietzは25%から97%の経済収縮を予想したが、このようなことはアメリカでは起こっていない。仮にもし本当だとしても、Rietzのモデルやパラメーター、補強証拠についていくつかの他の欠陥が存在する。Rietzが提示したモデルでは、急速なインフレによる債券保持者の部分的なデフォルトが考慮されていない。またリスク回避度のパラメーターもRietzの分析において矛盾して用いられている。例えば、消費の25%の下落を示すためにリスク回避度が10であるとされているが、消費と株式リターンを説明する為にはリスク回避度が1とされている。最後にRietzの理論を補強するためにはより多くの歴史的な証拠が必要であると述べている。例えば、レア・ディザスターが起こると考えられている確率は原子爆弾が投下される以前には低くなければならず、キューバ危機以後よりもキューバ危機以前の方がその確率は高くなければならない。ゆえに、実質利子率はこれらの事象と相関していなくてはならないが、実際はそうではなかった。Mehra はRietzのシナリオはエクイティプレミアムパズルを解決するには非常に過激すぎたと結論付けている[4]。
発展
[編集]Xavier Gabaixはバローのモデルでは時間を通じて一定であったレア・ディザスターの被害の程度を時間によって変動するように変更したモデルを提案している[5]。Gabaixは自身の提示したモデルでエクイティプレミアムパズルを含めた10個のマクロ経済学、金融経済学における未解決問題が説明できると述べている。
参照
[編集]脚注
[編集]- ^ 閉鎖経済であるということ。
- ^ a b c d Barro, Robert (2006), “Rare Disasters and Asset Markets in the Twentieth Century”, The Quarterly Journal of Economics 121 (3): 823-866, JSTOR 25098810 2015年12月30日閲覧。
- ^ a b c d Mehra, Ranjish (2008), “The Equity Premium Puzzle: A Review”, Foundations and Trends in Finance 2 (1): 1–81, doi:10.1561/0500000006 2015年12月30日閲覧。
- ^ Gabaix, Xabier (2012), “Variable Rare Disasters: An Exactly Solved Framework for Ten Puzzles in Macro-Finance”, The Quarterly Journal of Economics 127 (2): 645-700, doi:10.1093/qje/qjs001
参考文献
[編集]- Ranjnish Mehra(2003). “The Equity Premium: Why Is It a Puzzle?”. 2009年3月9日閲覧。
- New Economist(2005). “New Economist on Barro and the Equity Premium Puzzle”. Mehra. 2009年3月9日閲覧。








