パドヴァン数列

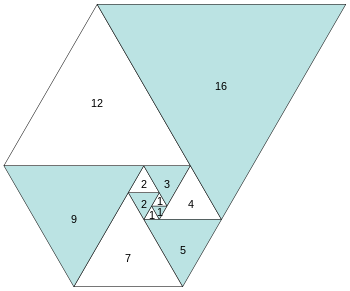パドヴァン数列の大きさの辺長を有する正三角形を並べた図

パドヴァン数列は、漸化式 $a_{0}=a_{1}=a_{2}=1,\,a_{n}=a_{n-2}+a_{n-3}$ で表される数列である。

第0～25項（4桁未満）の値は次のとおりである：

1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, 351, 465, 616, 816, ... （オンライン整数列大辞典の数列 A000931）

この、各項が2つ前と3つ前の項の和で与えられる数列は、イタリアの建築家リチャード・パドヴァンにちなんでパドヴァン数列と呼ばれている。

性質

• パドヴァン数列の母関数は次のとおりとなる：

$G(a_{n};x)={\frac {1+x}{1-x^{2}-x^{3}}}$

• 別途、$n\geq 5$ である各項は1つ前と5つ前の項の和としても与えられる。すなわち、

$a_{n}=a_{n-1}+a_{n-5}$

• ペラン数 $p_{n}$ とは、次の関係にある：

$p_{n}=a_{n+1}+a_{n-10}$

• 特性方程式：

$x^{3}-x-1=0$

の唯一の実数解より、パドヴァン数列（ペラン数列も然り）の連続する2項の比の値はプラスチック数

$\rho ={\sqrt[{3}]{\frac {9+{\sqrt {69}}}{18}}}+{\sqrt[{3}]{\frac {9-{\sqrt {69}}}{18}}}=1.324717957244746025960908854\cdots$

に次第に近づくことになる。

外部リンク

• Weisstein, Eric W. "Padovan Sequence". mathworld.wolfram.com (英語).