シルヴェスター–ガライの定理

シルヴェスター–ガライの定理（シルヴェスター–ガライのていり^[1]、英: Sylvester–Gallai theorem）は、幾何学において、平面上の有限個の点のうち、ちょうど2点のみを通るまたはすべての点を通る直線が存在する事を示す定理^[2]^[3]。1893年にこの問題を提起したジェームス・ジョセフ・シルヴェスターと、1944年に最初の証明を発表したティボル・ガライ（英語版、ハンガリー語版）に因んで命名された。

平面上の有限個の点のうち、ちょうど2点のみを通る直線は「ordinary line^{[訳語疑問点]}」と呼ばれる。シルヴェスタ–ガライの定理を別の方法で表現すると、平面上の有限個の点であって少なくとも1つの点が他の2点と共線でなければ、その有限個の点の集合はordinary lineを持つ、となる。より強い定理によれば、（すべての点が一直線上にある、ということがない）有限個の点の集合には、線型数以上のordinary lineが存在する。ordinary lineを発見するアルゴリズムの時間計算量は、 $n$ 点の集合に対して $O(n\log n)$ である。

歴史

シルヴェスタ–ガライの定理は、J. J. Sylvester (1893)によって提起された。 Kelly (1986)は、シルヴェスターは複素射影平面（英語版）上の三次曲線の9つの変曲点が、9点と12直線の配置（英語版）（ヘッセ配置（英語版））を成すという代数幾何学の問題に触発されたことを示唆している。シルヴェスター–ガライの定理はこの9つの変曲点がすべて実座標を持つことは不可能であることを示している^[4]。

H. J. Woodall (1893a, 1893b) は、シルヴェスター–ガライの定理の短い証明を発見したと主張したが、発表する時点ですでに、証明が不完全であることが指摘されていた。Eberhard Melchior (1941)は、定理の射影幾何学的な双対を示すことで、正確で強力な定理を得た。Paul Erdős (1943) は、メルヒオールの証明に気づかぬまま^[5]、定理を予想として述べ、その後にティボル・ガライや他の数学者が証明した^[6]。

1951年の評論では、エルデシュは「ガライの定理」の名を使用した^[7]。1954年には、レナード・ブルーメンタール（英語版）の評論で「シルヴェスター–ガライの定理」という名称が使われた^[8]。

同値な定理

ordinary lineの存在問題は、ユークリッド平面の代わりに射影平面RP²で考えることで、ordinary lineの双対となる点の問題としても考えることができる。射影平面は通常のユークリッド平面上の点に"無限遠"を付加することで構築される。しかし、無限遠に付加された点は、ordinary lineを持たない点の集合を作るのに役立つわけではない。これは、射影平面上の任意の有限個の点が、点と直線の接続関係の同様の組み合わせパターンを持つユークリッド点の集合に変換されるためである。したがって、ユークリッド平面と射影平面のどちらかに存在する交点と直線のパターンは、もう一方の平面にも存在する。にもかかわらず、射影的な観点は点と直線の配置を簡単に述べることができる。特に、射影幾何学の双対性（英語版）を使用することができることが重要である。この双対性の下、ordinary lineの存在は、非自明な配置 (Arrangement of lines) の有限個の直線上の、RP²上の有限個の点（ordinary point^{[訳語疑問点]}）の存在に置き換えることができる。ここで直線の配置が自明であるとは、すべての直線が共点であることで、非自明であるとは、あるordinary pointがちょうど2直線に属する状態を示す^[5]。

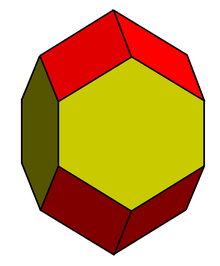
直線の配置はゾーン多面体（generator^{[訳語疑問点]}と呼ばれる直線の有限集合のミンコフスキー和から成る多面体）と近い組み合わせ的構造を持つ。この関係において、ゾーン多面体の対面の組は、射影平面上の直線の配置の交点と各generatorに一致する。対面の組の個数は、交点の数の2倍である。

例えば、長菱形十二面体は5本のgeneratorを持つゾーン多面体で、六角形の対面の組が2つ、平行四辺形の対面の組が4つ存在する。5本の直線の配置の対応において、3直線の組の2つが交差し、六角形の対面に対応する。また、残りの直線はordinary pointで交差し、平行四辺形の対面の組に対応する。ゾーン多面体の観点から、シルヴェスター-ガライの定理を言い換えると、すべてのゾーン多面体は1つ以上の）平行四辺形を持つ、となる。より強力には、平面上の $n$ 点の集合は少なくとも $t_{2}(n)$ 個のordinary linesを持ち、 $n$ 本のgeneratorを持つゾーン多面体は少なくとも $2t_{2}(n)$ 個の平行四辺形の面を持つことが保証される^[9]。

証明

シルヴェスター-ガライの定理はさまざなな方法で証明されてきた。ガライの1944年の証明は、ユークリッド幾何学と射影幾何学を交互に切り替えて、点を傾きが0に近いordinary lineに変換するというものである（詳しくはBorwein & Moser (1990)を参照されたい）。1941年のメルヒオールの証明では、射影幾何学の双対性を用いて、問題を直線の配置に置き換え、オイラーの多面体公式を使った。リロイ・ミルトン・ケリー（英語版）の証明は、0でない最小の距離にある点を繋ぐ直線はordinaryになることを背理法によって示した。またスタインバーグ（Steinberg）の早期の証明に続いて、コクセターは、傾きの計量と、ガライとケリーの証明に現れた距離の概念を不必要とする代わりに、順序幾何学（英語版）の公理を使った定理のみを使用して証明した。

ケリーの証明

次はリロイ・ミルトン・ケリー（英語版）による証明である。Aigner & Ziegler (2018) はケリーの証明を、数多の証明の中で"simply the best"であると述べている^[10]。

$S$ を共線でない点の有限集合とする。少なくとも $S$ の2点を含む直線を、connecting lineと定義する。 $S$ の有限性より、 $S$ は点とconnecting lineの距離が最小となるような1点 $P$ と1本のconnecting line $l$ を持っている必要がある。ケリーは $l$ がordinaryであることを背理法によって証明した^[10]。

$l$ をordinaryでないと仮定しよう。 $l$ は少なくとも $S$ に属する3点以上を通る必要がある。これら共線点のうち2つ以上は、 $l$ への $P$ の直交射影 $P'$ に関して同じ側にある。この2点を $B,C$ と定義する。ただし、 $C,B,P'$ はこの順で並んでいるとする。 $m$ を $CP$ を通るconnecting line、 $B'$ を $B$ の $m$ への直交射影とすれば、 $△ PP'C,△ BB'C$ が相似かつ $|△ PP'C | > |△ BB'C |$ であることより、 $BB'$ は $PP'$ より短い^[10]。

しかし、これは $P,l$ の定義に矛盾する。これは $l$ がordinaryでないとした仮定が偽であることを意味する。よって題意は示された^[10]。

メルヒオールの証明

1941年（エルデシュの問題発表とガライの証明の前）、メルヒオールは、射影平面上の非自明な直線の配置は、3つ以上のordinary pointsを持つことを示した。双対性より、非自明な点の集合は3つ以上の ordinary linesを持つことを意味する^[11]。

メルヒオールは、射影平面に埋め込まれた（英語版）任意のグラフについて、射影平面のオイラー標数 $V - E + F$ は1でなければならないことに気づいた。ここで、 $V,E,F$ はそれぞれ、グラフの頂点、辺、面の個数。射影平面上の非自明な直線の配置は、面は3辺以上で囲まれ、辺は2面で囲まれるようなグラフを定義する。そのため、二重に数える（英語版）ことで不等式 $F\leq 2E/3$ を得る。この不等式によって、オイラー標数から $F$ を取り除くことより $E\leq 3V-3$ が証明できる。しかしもし、配置上のすべての頂点が3以上の直線の交点であるならば、辺の総数は $3 V$ 以上であるが、これは不等式に矛盾する。したがって、いくつかの頂点は2直線のみの交点でなければならず、メルヒオールの慎重な分析が示すように、3以上のordinary verticesが少なくとも不等式 $E\leq 3V-3$ を満たす必要がある^[11]。

Aigner & Ziegler (2018) の指摘のように、ordinary vertexの存在に関する議論は、1944年、ノーマン・スティーンロッド（英語版）によって与えられた。スティーンロッドはordinary lineの問題の双対を明示的に応用した^[12]。

メルヒオールの不等式

同様の議論で、メルヒオールはより一般的な結果を証明することができた。任意の $k\geq 2$ において、 $t_{k}$ を $k$ 本の直線が成す点の数として、次の式が成立する^[11]。

\displaystyle \sum _{k\geq 2}(k-3)t_{k}\leq -3.

同値な表現として、

\displaystyle t_{2}\geqslant 3+\sum _{k\geq 4}(k-3)t_{k}.

公理数学

H. S. M. Coxeter (1948, 1969)はケリーの証明のユークリッド距離の使用は不必要に強力で、"like using a sledge hammer to crack an almond"（アーモンドを砕くために大型ハンマーを使うようなものだ）と述べた。代わりにコクセターは順序幾何学において証明を行った^[13]。コクセターの証明は1944年のスタインバーグによって与えられた証明の変形である^[14]。最小の公理集合を見つける問題は逆数学の定理を証明する必要がある。詳細はこの問題に関する研究のPambuccian (2009)を見よ。

シルヴェスター-ガライの定理の通常の主張は構成幾何学（英語版）においては有効でない。構成幾何学で拒否される排中律の弱いものであるLPO (Limited principle of omniscience) を意味するためである。にもかかわらず、構成解析の公理の範囲のシルヴェスター-ガライの定理の定理は定式化が可能で、ケリーの証明を構成幾何学の公理の下で、有効となるように適応することができる^[15]。

ordinary lineの捜索

ordinary lineの存在のケリーの証明では、2点を通る直線と点の距離が最小となるような組を見つける事でordinary lineを見つけることができる。 Mukhopadhyay & Greene (2012)はこの方法で力まかせ探索を用いてordinary lineを捜索する時間計算量は $O(n^{3})$ であることを報告した。しかし、Edelsbrunner & Guibas (1989)は $O(n^{2})$ で発見するアルゴリズムを開発した。これは、集合の中の3点からなる三角形で最小のものを探すことの副産物であった。彼らの同様の論文にて、（メルヒオールとスティーンロッドの証明を用いて）、双対の配置でordinary pointを見つける方法が同様の時間 $O(n^{2})$ であることを示した。 Mukhopadhyay, Agrawal & Hosabettu (1997)は最初に（ケリーの証明を必要としない方法で）1つのordinary lineを発見する時間 $O(n\log n)$ の方法を開発した。同じ時間ではあるがより単純なアルゴリズムがMukhopadhyay & Greene (2012)によって述べられている。

Mukhopadhyay & Greene (2012)のアルゴリズムはコクセターの証明をもとにしている。次の手順で示される。

与えられた点の凸包の頂点から点 $p_{0}$ を選ぶ。
直線 $\ell _{0}$ を、 $p_{0}$ と他の凸包の頂点を通る直線として構築する。
他の与えられた点を $p_{0}$ と成す角で並べ替え、同じ角のものをグループ化する。
グループ内のある点が孤立していれば、その点と $p_{0}$ を通る直線がordinaryである。
それぞれの2つの連続するグループに対して、2直線を、一方のグループ内の $p_{0}$ と最も近い点と、もう一方の最も近い点を通る直線とする。
このようにしてできた直線の集合内のそれぞれの直線 $\ell _{i}$ に対して、 $\ell _{0}$ と $\ell _{i}$ の交点を取る。
この交点が $p_{0}$ と一番近いような $\ell _{i}$ がordinary lineとなる。

著者らの証明のように、このアルゴリズムでordinary lineを必ず見つけることができる。4つ目のステップで見つかった場合は構成幾何学によるもの、7つ目のステップで見つかったものは背理法によるもので、もし7つ目の段階で見つかったものがordinary lineでなければ、交点らと $p_{0}$ を通る直線がordinary lineとして存在するが、これは4つ目の段階で発見されるべきものである^[16]。

ordinary lineの個数

シルヴェスター-ガライの定理は点の配置についてordinary lineの存在は述べているが、ordinary lineの個数については述べていない。 $t_{2}(n)$ を $n$ つの共線でない点の集合のordinary lineの最小の個数とする。メルヒオールの証明では $t_{2}(n)\geq 3$ が示された。 de Bruijn and Erdős (1948)は $n$ が増えるにつれて $t_{2}(n)$ は無限大へ発散していくと提起した。Theodore Motzkin (1951) は $t_{2}(n)\geq {\sqrt {n}}$ を証明して、予想が正しいことを示した。 Gabriel Dirac (1951)は $t_{2}\geq \lfloor n/2\rfloor$ を予想した。これは現在ディラック-モツキン予想（Dirac–Motzkin conjecture）と呼ばれている（詳細はBrass, Moser & Pach (2005, p. 304)を参照）。 Kelly & Moser (1958) は $t_{2}(n)\geq 3n/7$ を証明している。

ディラックの予想した下限は漸近的には最もよいもので、4超過の偶数 $n$ の上限 $t_{2}(n)\leq n/2$ と対応する。Károly Böröczkyによる上限を達成した構築は、射影平面上の正 $m$ 角形と頂点の組で決定される方向の無限遠点 $m$ 個（延べ $n = 2 m$ 個）から構築される。これらの点の組は $m(m-1)/2$ 個あるが、 $m$ 個のみの方向を決定する。この配置では $m$ 個のordinary lineを持ち、頂点 $v$ とそれに隣り合う2頂点と共線な無限遠点を結ぶ点になる。実射影平面の任意の有限の配置のように、この構成はordinary lineの数を変えずにすべての点が有限点となるように帰ることができる^[17]。

奇数 $n$ において、ディラックの予想の下限 $t_{2}(n)=(n-1)/2$ に一致する例は2つしか知られていない。1つはKelly & Moser (1958)の考案した正三角形の頂点、重心、辺の中点の7点から成る構成である。この7点はordinary lineを3つのみ持つ。3つのordinary lineを持つ点と直線の配置（英語版）はユークリッド平面上では単一の直線に置き換えることはできないが、ファノ平面（英語版）として知られる有限の射影空間を作る。この接続のために、ケリー-モザーの例はnon-Fano configurationとしても呼ばれる^[18]。他の例にマッキー（McKee）の考案した^[17] 、1辺を共有する2つの正五角形の頂点と、共有辺の中点と4つの無限遠点の延べ13点から成る配置がある。これは6つのordinary linesを持つ。 Böröczkyの構成を修正すれば、奇数n個の点で $3\lfloor n/4\rfloor$ 個のordinary lineを持つ配置が導かれれる^[19]。

Csima & Sawyer (1993) は $n$ が7である場合を除き、 $t_{2}(n)\geq \lceil 6n/13\rceil$ が成立することを証明した。漸近的には、証明された $n/2$ の上限の $12/13\approx 92.3\%$ である。 $n=7$ の場合、ケリー-モザーの例 $t(7)\leq 3$ が反例となって除外される。しかし、Csima–Sawyerの境界が $n=7$ においても有効だったならば、 $t_{2}(7)\geq 4$ が主張されただろう。

似た結果にベックの定理（英語版）がある。これは少数の点の直線の数と一本の直線上の点の数がトレードオフされることを延べている^[20]。

ベン・グリーンとテレンス・タオは、十分大きい点の集合に対して（適当に $n_{0}$ を選択したとき $n>n_{0}$ となるようにして）、ordinary lineの数は確かに少なくとも $n/2$ となること示した。更に、 $n$ が奇数ならば、ordinary lineの数はある定数 $C$ が存在して少なくとも $3n/4-C$ となる。したがって、Böröczkyによる構成は最良であったことが判明した。ordinary lineの個数の最小化は、グリーンとタオが十分大きい場合について証明した、3点を通る直線の個数の最大化問題であるOrchard-planting problem (Orchard-planting problem) にも深く関係している^[21]。ordinary pointを探すような双対の状態において、擬似直線の配置のordinary pointの最小を考えることができる。この場合においては、Csima-Sawyerの $\lceil 6n/13\rceil$ の下限は有効であるが^[22]、グリーンとタオの漸近的な境界 $n/2$ は有効であるかは知られていない。

connecting lineの数

ポール・エルデシュの気づきのように、シルヴェスター-ガライの定理は共線でない $n$ 点の集合について少なくとも $n$ つの異なる直線が決定できることを意味する。この結果はド・ブルイン-エルデシュの定理（英語版）として知られる。基本的な場合としては、 $n=3$ の場合が自明である。値の大きい $n$ については、（残りの点がすべて共線とならないように注意して）1本のordinary lineとその直線上の2点のうち1点を削除して、 $n$ 点を $n-1$ 点に減らすことができる。よって、定理は数学的帰納法から示すことができる。ニアペンシル（near-pencil）と呼ばれる $n-1$ 個の共線点と、それらと共線でないある1点から成る配置が下限の例となる^[19]。

一般化

シルヴェスター-ガライの定理は、ユークリッド平面平面上の色付きの点の集合や、代数的または距離空間的に定義される点と直線の系に一般化できる。より一般にはこれら定理のバリエーションは、ordinary lineを持たない点の集合を避けるため、有限集合に対するものとなっている。

色付きの点

色付きの点におけるシルヴェスター-ガライの定理は、1960年代中期にロナルド・グラハムが提起し、ドナルド・ニューマン（英語版）が広めた。 2つの色に分けられた（すべてが同一直線上にはない）有限の点の集合について、2つ以上のすべて同色の点を通る直線が存在するかどうかを考える。集合と集合族の言葉では、（すべてが同一直線上にはない）有限の点の共線部分集合の族は性質B（英語版）を持つことはできない、と表現できる。証明はテオドール・モツキン（英語版）によって発表されたが、公表はされなかった。最初に証明を公表したのはChakerian (1970)である^[23]。

非実座標

ユークリッド平面または射影平面が実数の組、座標を用いて定義できるように（ユークリッド平面は直交座標系、射影平面は同次座標系（英語版））、点と直線の系の抽象的な類似物は、数と座標を用いて定義できる。シルヴェスター-ガライの定理は有限体上でこのように定義された幾何学では適応できない。つまりファノ平面（英語版）のような有限幾何学において、すべての点の集合のordinary lineは存在しない^[10]。

また、シルヴェスター-ガライの定理は複素数や四元数の組の座標を持つ幾何学においても直接は成立しないが、より複雑な類似物であれば成立する。例えば、複素射影平面（英語版）には、9つの点（三次曲線の変曲点）の配置であるヘッセ配置（英語版）がある。この配置におけるordinary lineは存在しない。このような配置は、シルヴェスター-ガライ配置（英語版）として知られ、ユークリッド平面上では成立することはない。シルヴェスター-ガライの定理の他の方法で述べると、シルヴェスター-ガライ配置が共線性を保ちつつユークリッド平面に埋め込まれるとき、配置内の点は常に一本の直線上にある、となる。したがってヘッセ配置の例は、複素射影平面（英語版）では偽であることが分かる。しかし、Kelly (1986)はシルヴェスター-ガライの定理の複素数への類似物として、シルヴェスター-ガライ配置（英語版）を複素射影平面に埋め込んだ時、すべての点は2次元部分空間上になければならないことを示した。つまり、アフィン包が全体の空間であるような3次元複素空間上の点の集合は必ず1つのordinary lineを持ち、またordinary lineの線型数を持たなければならない^[24]。同様に、Elkies, Pretorius & Swanepoel (2006) はシルヴェスター-ガライ配置（英語版）四元数で定義される空間に埋め込むとき、それらの点は必ず3次元部分空間上になければならないことを示した。

マトロイド

ユークリッド平面上の点の任意の集合とそれらを繋ぐ直線は、ランク3の有向マトロイド（英語版）の成分と平面に抽象化される。実数でない数の体系で定義される幾何学の点と直線はマトロイドを成すが、必ずしも有向マトロイドを成すわけではない。この状況において、Kelly & Moser (1958)のordinary lineの個数の下限の結果は、有向マトロイドへ一般化できる。ランク3の $n$ 成分の有向マトロイドは、 $3n/7$ 個の、2点を通る直線を持つ。あるいは、より少数の2点を通る直線の持つランク3のマトロイドは無向である必要がある^[25]。 2点のみを通る直線がないようなマトロイドはシルヴェスターマトロイド（英語版）と呼ばれる。関連して、7点と3つのordinary lineを持つケリー-モザー配置は、GF(4)表現可能マトロイド（英語版）における禁止マイナー（英語版）を作る^[18]。

距離幾何学

シルヴェスター-ガライの定理の他の一般化において、Chvátal (2004)によって任意の距離空間へ予想が行われChen (2006)によって解決された。この一般化では、距離空間上の3点が三角不等式の等号を満たすとき共線であると定義され、直線は、既に直線上にある2点と共線である点の全体の集合であると定義された。ChvátalとChenによる一般化はすべての有限距離空間は、すべての点を含むような直線かただ2点のみを通る直線を持つことを示した^[26]。

脚注

出典

Aigner, Martin; Ziegler, Günter M. (2018), “Chapter 11. Lines in the plane and decomposition of graphs”, Proofs from THE BOOK (6th ed.), Springer, Theorem 1, pp. 77–78, doi:10.1007/978-3-662-57265-8_11, ISBN 978-3-662-57265-8
Basit, Abdul; Dvir, Zeev; Saraf, Shubhangi; Wolf, Charles (2019), “On the number of ordinary lines determined by sets in complex space”, Discrete & Computational Geometry 61 (4): 778–808, arXiv:1611.08740, doi:10.1007/s00454-018-0039-4, MR3943495
Beck, József (1983), “On the lattice property of the plane and some problems of Dirac, Motzkin, and Erdős in combinatorial geometry”, Combinatorica 3 (3–4): 281–297, doi:10.1007/BF02579184, MR0729781
Björner, Anders; Las Vergnas, Michel; Sturmfels, Bernd; White, Neil; Ziegler, Günter M. (1993), Oriented matroids, Encyclopedia of Mathematics and its Applications, 46, Cambridge: Cambridge University Press, p. 273, ISBN 0-521-41836-4, MR1226888
Borwein, P.; Moser, W. O. J. (1990), “A survey of Sylvester's problem and its generalizations”, Aequationes Mathematicae 40 (1): 111–135, doi:10.1007/BF02112289, MR1069788
Brass, Peter; Moser, William; Pach, János (2005), Research problems in discrete geometry, Berlin: Springer, ISBN 0-387-23815-8
de Bruijn, N. G.; Erdős, P. (1948), “A combinatioral [sic] problem”, Indagationes Mathematicae 10: 421–423, MR0028289
Chakerian, G. D. (1970), “Sylvester's problem on collinear points and a relative”, American Mathematical Monthly 77 (2): 164–167, doi:10.2307/2317330, JSTOR 2317330, MR258659, https://jstor.org/stable/2317330
Chen, Xiaomin (2006), “The Sylvester–Chvátal theorem”, Discrete & Computational Geometry 35 (2): 193–199, doi:10.1007/s00454-005-1216-9, MR2195050
Chvátal, Vašek (2004), “Sylvester–Gallai theorem and metric betweenness”, Discrete & Computational Geometry 31 (2): 175–195, doi:10.1007/s00454-003-0795-6, MR2060634
Coxeter, H. S. M. (1948), “A problem of collinear points”, American Mathematical Monthly 55 (1): 26–28, doi:10.2307/2305324, JSTOR 2305324, MR24137, https://jstor.org/stable/2305324
Coxeter, H. S. M. (1969), “12.3 Sylvester's problem of collinear points”, Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, pp. 181–182, ISBN 0-471-50458-0
Crowe, D. W.; McKee, T. A. (1968), “Sylvester's problem on collinear points”, Mathematics Magazine 41 (1): 30–34, doi:10.2307/2687957, JSTOR 2687957, MR0235452, https://jstor.org/stable/2687957
Csima, J.; Sawyer, E. (1993), “There exist $6n/13$ ordinary points”, Discrete & Computational Geometry 9: 187–202, doi:10.1007/BF02189318, MR1194036
Dirac, G. (1951), “Collinearity properties of sets of points”, Quarterly Journal of Mathematics 2: 221–227, Bibcode: 1951QJMat...2..221D, doi:10.1093/qmath/2.1.221, MR0043485
Edelsbrunner, Herbert; Guibas, Leonidas J. (1989), “Topologically sweeping an arrangement”, Journal of Computer and System Sciences 38 (1): 165–194, doi:10.1016/0022-0000(89)90038-X, MR990055
Elkies, Noam; Pretorius, Lou M.; Swanepoel, Konrad J. (2006), “Sylvester–Gallai theorems for complex numbers and quaternions”, Discrete & Computational Geometry 35 (3): 361–373, arXiv:math/0403023, doi:10.1007/s00454-005-1226-7, MR2202107
Erdős, P. (1943), “Problem 4065”, American Mathematical Monthly 50 (1): 65–66, doi:10.2307/2304011, JSTOR 2304011, https://jstor.org/stable/2304011
Erdős, P. (1982), “Personal reminiscences and remarks on the mathematical work of Tibor Gallai”, Combinatorica 2 (3): 207–212, doi:10.1007/BF02579228, MR0698647
Geelen, J. F.; Gerards, A. M. H.; Kapoor, A. (2000), “The excluded minors for GF(4)-representable matroids”, Journal of Combinatorial Theory, Series B 79 (2): 247–299, doi:10.1006/jctb.2000.1963, MR1769191, オリジナルの2010-09-24時点におけるアーカイブ。
Green, Ben; Tao, Terence (2013), “On sets defining few ordinary lines”, Discrete & Computational Geometry 50 (2): 409–468, arXiv:1208.4714, doi:10.1007/s00454-013-9518-9, MR3090525
Grünbaum, Branko (1999), “Monochromatic intersection points in families of colored lines”, Geombinatorics 9 (1): 3–9, MR1698297
Kelly, L. M. (1986), “A resolution of the Sylvester–Gallai problem of J. P. Serre”, Discrete and Computational Geometry 1 (2): 101–104, doi:10.1007/BF02187687, MR0834051
Kelly, L. M.; Moser, W. O. J. (1958), “On the number of ordinary lines determined by $n$ points”, Canadian Journal of Mathematics 10: 210–219, doi:10.4153/CJM-1958-024-6, MR0097014
Lenchner, Jonathan (2008). Sylvester-Gallai results and other contributions to combinatorial and computational geometry (Ph.D. Thesis).
Mandelkern, Mark (2016), “A constructive version of the Sylvester–Gallai theorem”, Acta Mathematica Hungarica 150: 121–130, arXiv:2402.03662, doi:10.1007/s10474-016-0624-z, MR3542040
Melchior, E. (1941), “Über Vielseite der Projektive Ebene”, Deutsche Mathematik 5: 461–475
Motzkin, Th. (1951), “The lines and planes connecting the points of a finite set”, Transactions of the American Mathematical Society 70 (3): 451–464, doi:10.2307/1990609, JSTOR 1990609, MR0041447, https://jstor.org/stable/1990609
Mukhopadhyay, A.; Agrawal, A.; Hosabettu, R. M. (1997), “On the ordinary line problem in computational geometry”, Nordic Journal of Computing 4 (4): 330–341, MR1607014
Mukhopadhyay, Asish; Greene, Eugene (2012), “The ordinary line problem revisited”, Computational Geometry: Theory and Applications 45 (3): 127–130, doi:10.1016/j.comgeo.2011.10.003, MR2853475
Pach, János; Sharir, Micha (2009), “Chapter 1. Sylvester–Gallai Problem: The Beginnings of Combinatorial Geometry”, Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical Surveys and Monographs, 152, American Mathematical Society, pp. 1–12
Pambuccian, Victor (2009), “A reverse analysis of the Sylvester–Gallai theorem”, Notre Dame Journal of Formal Logic 50 (3): 245–260, doi:10.1215/00294527-2009-010, MR2572973
Shephard, G. C. (1968), “Twenty problems on convex polyhedra, part I”, The Mathematical Gazette 52 (380): 136–156, doi:10.2307/3612678, JSTOR 3612678, MR231278, https://jstor.org/stable/3612678
Steinberg, R.; Buck, R. C.; Grünwald, T.; Steenrod, N. E. (1944), “Three point collinearity (solution to problem 4065)”, American Mathematical Monthly 51 (3): 169–171, doi:10.2307/2303021, JSTOR 2303021, https://jstor.org/stable/2303021
Sylvester, J. J. (1893), “Mathematical question 11851”, The Educational Times 46 (383): 156
Woodall, H. J. (1893a), “Mathematical question 11851 answered”, The Educational Times 46 (385): 231
Woodall, H. J. (1893b), “Mathematical question 11851 answered”, Mathematical Questions and Solutions from the Educational Times 59: 98

外部リンク

Malkevitch, Joseph (2003), “A discrete geometrical gem”, AMS Feature Column (American Mathematical Society), オリジナルの2006-10-10時点におけるアーカイブ。
Weisstein, Eric W. "Ordinary Line". mathworld.wolfram.com (英語).
Proof presentation by Terence Tao at the 2013 Minerva Lectures
複素版Sylvester-Gallaiの定理と超平面配置の対数的ベクトル場の分裂型 - 阿部拓郎

[1] 『新訂版　数学用語英和辞典: 和英索引付き』近代科学社、2020年12月2日。ISBN 978-4-7649-0624-2。

[2] Chvátal, Vašek『ポール・エルデス：離散数学の魅力: 伝説の講義』近代科学社、2023年8月25日。ISBN 978-4-7649-0662-4。

[3] 『ボロバシュ数学の技法』丸善出版、2022年。ISBN 978-4-621-30731-1。

[FOOTNOTEElkiesPretoriusSwanepoel2006-4] Elkies, Pretorius & Swanepoel (2006).

[FOOTNOTEBorweinMoser1990-5] Borwein & Moser (1990).

[stein44-6] Steinberg et al. (1944); Erdős (1982).

[7] MR0041447

[8] MR0056941

[FOOTNOTEShephard1968-9] Shephard (1968).

[FOOTNOTEAignerZiegler2018-10] Aigner & Ziegler (2018).

[FOOTNOTEMelchior1941-11] Melchior (1941).

[12] Aigner & Ziegler (2018, p. 92); Steenrod's proof was briefly summarized in Steinberg et al. (1944).

[13] Aigner & Ziegler (2018); Pambuccian (2009).

[14] Coxeter (1948); Pambuccian (2009).

[FOOTNOTEMandelkern2016-15] Mandelkern (2016).

[FOOTNOTEMukhopadhyayGreene2012-16] Mukhopadhyay & Greene (2012).

[CM68-17] Crowe & McKee (1968).

[ggk00-18] Geelen, Gerards & Kapoor (2000).

[ps09-19] Pach & Sharir (2009)

[FOOTNOTEBeck1983-20] Beck (1983).

[FOOTNOTEGreenTao2013-21] Green & Tao (2013).

[FOOTNOTELenchner2008-22] Lenchner (2008).

[23] For the history of this variation of the problem, see also Grünbaum (1999)

[FOOTNOTEBasitDvirSarafWolf2019-24] Basit et al. (2019).

[25] Björner et al. (1993).

[26] Chvátal (2004); Chen (2006); Pambuccian (2009)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]