コンウェイ円

コンウェイ円と、その円周上の六つの点。Iは三角形の内心、等長の辺は同じ色で塗り分けてある。

ユークリッド幾何学において、コンウェイ円（コンウェイえん、英:Conway circle）とは三角形の辺を拡張した直線上の、頂点からその対辺と同じ長さの距離にある点を通る円である。 そのような6点が共円であるという定理をコンウェイ円の定理(Conway circle theorem)と言う 。名称はジョン・ホートン・コンウェイに由来する。

証明

同じ長さの線分は同色で示してある。${\begin{aligned}\triangle IF_{c}P_{a}&\cong \triangle IF_{c}Q_{b}\cong \triangle IF_{a}P_{b}\\&\cong \triangle IF_{a}Q_{c}\cong \triangle IF_{b}P_{c}\\&\cong \triangle IF_{a}Q_{a}\\\Rightarrow \,|IP_{a}|&=|IQ_{a}|=|IP_{b}|=|IQ_{b}|\\&=|IP_{c}|=|IQ_{c}|\end{aligned}}$

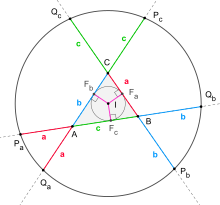
I を三角形ABCの内心、rを内接円の半径、sを半周長、F_a, F_b , F_cを内接円と辺a, b ,cの接点とする。

IF_a, IF_b , IF_cはそれぞれa, b ,cの垂線であるからピトーの定理より|AF_c|=|AF_b|=s-a, |BF_c|=|BF_a|=s-b, |CF_a|=|CF_b|=s-cである。6つの三角形 IF_cP_a, IF_cQ_b, IF_aP_b, IF_aQ_c, IF_bQ_a ,IF_bP_c aはすべて、|AF_c|+|BF_c|+|CF_a|=sとrと等しい長さの辺を持ち、また直角三角形である。したがって二辺夾角相等より6つの三角形はすべて合同で、|IP_a|=|IQ_a|=|IP_b|=|IQ_b|=|IP_c|=|IQ_c| が成り立ち、6点P_a, Q_a, P_b, Q_b, P_c ,Q_c はIとの距離が等しく、Iを中心として共円である。

性質

コンウェイ円の半径は

${\sqrt {r^{2}+s^{2}}}$

である。ただし $r$ は内接円の半径、 $s$は半周長である。

一般化

コンウェイ円の定理

コンウェイ円の定理は次のように一般化できる。

△ABCと直線AB上の点Pについて、符号付き距離で、BP=BQ, CQ=CR, AR=AS,BS=BT,CT=CUをみたす点を、それぞれQ,TはBC上に、R,UはCA上に、SはAB上に作ったとき、AU = APで PQRSTU は共円である。

PをAB上のBP=bを満たすような外側の点とすることで、コンウェイ円の定理を得る。

関連

• 九点円
• 六点円
• フールマン円
• レスター円
• 三角形の円

外部リンク

• Kimberling, Clark.. “Encyclopedia of Triangle Centers”. 2024年3月26日閲覧。
• Conway’s Circle Theorem as special case of Side Divider Theorem at Dynamic Geometry Sketches, interactive geometry sketches.