三角関数 (さんかくかんすう、英 : trigonometric function )とは、平面三角法 における、角 の大きさと線分 の長さの関係を記述する関数 の族 および、それらを拡張して得られる関数の総称である。鋭角 を扱う場合、三角関数の値は対応する直角三角形 の二辺の長さの比(三角比 )である。三角法に由来する三角関数 という呼び名のほかに、後述する単位円 を用いた定義に由来する円関数 (えんかんすう、英 : circular function
三角関数には以下の3つがある。
正弦 、sin (sin e正接 、tan (tan gent余弦 、cos (cos ine特に sin, cos は幾何学 的にも解析学 的にも良い性質を持っているので、様々な分野で用いられる。例えば波 や電気信号 などは正弦関数と余弦関数を組み合わせることで表現することができる。この事実はフーリエ級数 およびフーリエ変換 の理論として知られ、音声などの信号の合成や解析の手段として利用されている。他にもベクトル の外積 や内積 は正弦関数および余弦関数を用いて表すことができ、ベクトルを図形に対応づけることができる。初等的には、三角関数は実数 を変数 とする一変数関数として定義される。三角関数の変数の対応するものとしては、図形のなす角度や、物体の回転角、波や信号のような周期的 なものに対する位相 などが挙げられる。
三角関数に用いられる独特な記法として、三角関数の累乗 と逆関数 に関するものがある。通常、関数 f (x )(f (x ))2 = f (x )・f (x ) や (f (x ))−1 = 1/f (x ) のように書くが、三角関数の累乗は sin2 x のように書かれることが多い。逆関数 については通常の記法 (f −1 (x )sin−1 x などと表す(この文脈では従って、三角関数の逆数 は分数を用いて 1 / sinx (sin x )−1 などと表される)。文献あるいは著者によっては、通常の記法と三角関数に対する特殊な記法との混同を避けるため、三角関数の累乗を通常の関数と同様にすることがある。また、三角関数の逆関数として −1 と添え字する代わりに関数の頭に arc (Arc )とつけることがある(たとえば sin の逆関数として sin−1 の代わりに arcsin [Arcsin ]を用いる)。
三角関数に似た性質を持つ関数として、指数関数 や双曲線関数 、ベッセル関数 などがある。また、三角関数を利用して定義される関数としてしばしば応用されるものにsinc関数 がある。
∠C を直角とする直角三角形ABC直角三角形 において、1 つの鋭角 の大きさが決まれば、三角形 の内角 の和は 180° であることから他の 1 つの鋭角の大きさも決まり、3 辺の比も決まる。ゆえに、角度に対して辺比(三角比)の値を与える関数を考えることができる。
∠C を直角とする直角三角形 ABC において、それぞれの辺の長さを AB = h , BC = a , CA = b と表す(図を参照)。∠A = θ に対して三角形の辺の比 h : a : b
sin
θ
=
a
h
h
b
=
1
cos
θ
tan
θ
=
a
b
=
sin
θ
cos
θ
cos
θ
=
b
h
cosec
θ
=
h
a
=
1
sin
θ
b
a
=
1
tan
θ
{\displaystyle {\begin{aligned}\sin \theta &={\frac {a}{h}}\\{\frac {h}{b}}={\frac {1}{\cos \theta }}\\\tan \theta &={\frac {a}{b}}={\frac {\sin \theta }{\cos \theta }}\\\cos \theta &={\frac {b}{h}}\\\operatorname {cosec} \theta &={\frac {h}{a}}={\frac {1}{\sin \theta }}\\{\frac {b}{a}}={\frac {1}{\tan \theta }}\end{aligned}}}
という 3 つの値が定まる。それぞれ正弦 (sin e;正接 (tan gent;余弦 (cos ine;三角比 と呼ばれる。ある角 ∠A に対する余弦、余接はその角 ∠A の余角 (co-angle) に対する正弦、正接として定義される。
cos
θ
=
sin
(
90
∘
−
θ
)
=
sin
(
π
2
−
θ
)
tan
(
90
∘
−
θ
)
=
tan
(
π
2
−
θ
)
{\displaystyle {\begin{aligned}\cos \theta &=\sin \left(90^{\circ }-\theta \right)=\sin \left({\frac {\pi }{2}}-\theta \right)\\\tan \left(90^{\circ }-\theta \right)=\tan \left({\frac {\pi }{2}}-\theta \right)\end{aligned}}}
三角比は平面三角法 に用いられ、巨大な物の大きさや遠方までの距離を計算する際の便利な道具となる。角度 θ の単位 は、通常度 またはラジアン である。
三角比、すなわち三角関数の直角三角形を用いた定義は、直角三角形の鋭角に対して定義されるため、その定義域は θ θ = 90° (= π / 2)1/cos, tan が、θ = 0°(= 0)1/sin がそれぞれ定義されない。これは分母となる辺の比の大きさが 0 になるためゼロ除算 が発生し、その除算自体が数学的に定義されないからである。一般の角度に対する三角関数を得るためには、三角関数について成り立つ何らかの定理を指針として、定義の拡張を行う必要がある。後述する単位円による定義 は初等幾何学におけるそのような拡張の例である。他に同等な方法として、正弦定理 や余弦定理 を用いる方法などがある。
6種類の三角関数、単位円、θ = 0.7 ラジアンの角度に対する直線の図。直線の色が変わる点3点を考えたとき、1 、Sec(θ) 、Csc(θ) については原点から各点への線分の長さを表し、Sin(θ) 、Tan(θ) 、1 は各点のy成分を表す。Cos(θ) 、1 、Cot(θ) は各点の x 成分を表す。 単位円による、6つの三角関数が表す長さ 2 次元ユークリッド空間 R 2 単位円 {x (t )}2 + {y (t )}2 = 1 上の点を A = (x (t ), y (t )) とする。反時計回り を正の向きとして、原点と円周を結ぶ線分 OA と x 軸のなす角の大きさ ∠x OA を(媒介)変数 t として選ぶ。このとき実数 の変数 t に対する三角関数は以下のように定義される。
sin
t
=
y
cos
t
=
x
tan
t
=
y
x
=
sin
t
cos
t
{\displaystyle {\begin{aligned}\sin t&=y\\\cos t&=x\\\tan t&={\frac {y}{x}}={\frac {\sin t}{\cos t}}\end{aligned}}}
これらは順に正弦関数 (sin e function) 、余弦関数 (cos ine function) 、正接関数 (tan gent function) と呼ばれる。さらにこれらの逆数 として以下の 3 つの関数が定義される。
csc
t
=
1
y
=
1
sin
t
sec
t
=
1
x
=
1
cos
t
cot
t
=
x
y
=
1
tan
t
{\displaystyle {\begin{aligned}\csc t&={\frac {1}{y}}={\frac {1}{\sin t}}\\\sec t&={\frac {1}{x}}={\frac {1}{\cos t}}\\\cot t&={\frac {x}{y}}={\frac {1}{\tan t}}\end{aligned}}}
これらは順に余割関数 (cosec ant function) 、正割関数 (sec ant function) 、余接関数 (cot angent function) と呼ばれ、sin, cos, tan と合わせて三角関数 と総称される。特に csc, sec, cot は割三角関数 (かつさんかくかんすう)と呼ばれることがある。
この定義は 0 < t < π / 2 の範囲では直角三角形による定義 と一致する。
角度、辺の長さといった幾何学的な概念への依存を避けるため、また定義域 を複素数 に拡張するために、級数 (他の定義を採用した三角関数のテイラー展開 に一致する)を用いて定義することもできる。この定義は実数の範囲では単位円による定義と一致する。以下の級数は共に示される収束円内で収束 する。
sin
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
!
z
2
n
+
1
for all
z
,
cos
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
z
2
n
for all
z
,
tan
z
=
∑
n
=
1
∞
(
−
1
)
n
2
2
n
(
1
−
2
2
n
)
B
2
n
(
2
n
)
!
z
2
n
−
1
for
|
z
|
<
π
2
,
cot
z
=
∑
n
=
0
∞
(
−
1
)
n
2
2
n
B
2
n
(
2
n
)
!
z
2
n
−
1
for
0
<
|
z
|
<
π
,
sec
z
=
∑
n
=
0
∞
(
−
1
)
n
E
2
n
(
2
n
)
!
z
2
n
for
|
z
|
<
π
2
,
csc
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
−
2
2
n
)
B
2
n
(
2
n
)
!
z
2
n
−
1
for
0
<
|
z
|
<
π
.
{\displaystyle {\begin{aligned}\sin z&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}\quad {\text{for all}}\ z,\\\cos z&=\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}}{\left(2n\right)!}}z^{2n}\quad {\text{for all}}\ z,\\\tan z&=\sum _{n=1}^{\infty }{\frac {\left(-1\right)^{n}2^{2n}\left(1-2^{2n}\right)B_{2n}}{\left(2n\right)!}}z^{2n-1}\quad {\text{for}}\ |z|<{\frac {\pi }{2}},\\\cot z&=\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}2^{2n}B_{2n}}{\left(2n\right)!}}z^{2n-1}\quad {\text{for}}\ 0<|z|<\pi ,\\\sec z&=\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}E_{2n}}{\left(2n\right)!}}z^{2n}\quad {\text{for}}\ |z|<{\frac {\pi }{2}},\\\csc z&=\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}\left(2-2^{2n}\right)B_{2n}}{\left(2n\right)!}}z^{2n-1}\quad {\text{for}}\ 0<|z|<\pi .\end{aligned}}}
実関数 f (x )常微分方程式 の初期値問題
f
″
(
x
)
=
−
f
(
x
)
,
f
(
0
)
=
1
,
f
′
(
0
)
=
0
{\displaystyle f''(x)=-f(x),\;f(0)=1,\;f'(0)=0}
(1 )
の解として cosx を定義し、sinx を −d (cosx )/dx として定義できる[ 1] [ 2] g (x ) = f ' (x )
{
f
′
(
x
)
=
g
(
x
)
,
g
′
(
x
)
=
−
f
(
x
)
{\displaystyle {\begin{cases}f'(x)=g(x),\\g'(x)=-f(x)\end{cases}}}
(2 )
および初期条件 f (0) = 1, g (0) = 0
この他にも定積分による(逆三角関数を用いた)定義や複素平面の角の回転による定義などが知られている[ 1] [ 6] [ 7]
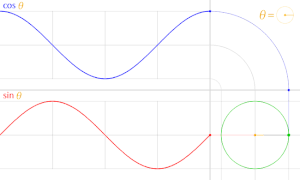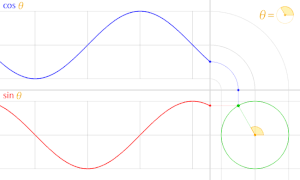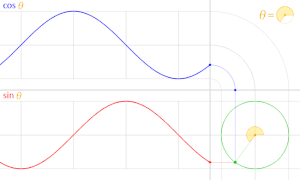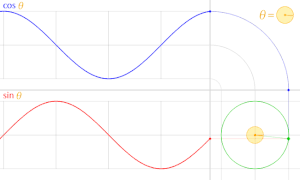
正円より得られる cosθ sinθ sinx cosx x 軸の正の部分となす角は
t
=
θ
+
2
π
n
(
0
≤
θ
<
2
π
,
n
∈
Z
)
{\displaystyle t=\theta +2\pi n\quad (0\leq \theta <2\pi ,\,n\in \mathbb {Z} )}
と表すことができ、θ を偏角 、t を一般角 という。
一般角 t が 2π 進めば点 P(cost , sint ) は単位円上を1周し元の位置に戻る。従って、
cos
(
t
+
2
π
n
)
=
cos
t
sin
(
t
+
2
π
n
)
=
sin
t
{\displaystyle {\begin{aligned}\cos(t+2\pi n)&=\cos t\\\sin(t+2\pi n)&=\sin t\end{aligned}}}
すなわち三角関数 cos, sin は周期 2π の周期関数 である。
ほぼ同様に、tan, cot は周期 π の周期関数、sec, csc は周期 2π の周期関数である。
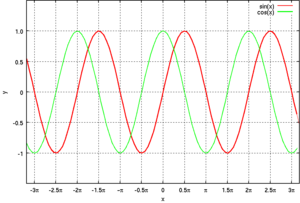
また、cosθ , sinθ のグラフの形は正弦曲線 である。
三角関数のグラフ: Sine(青実線 )、 Cosine(緑実線 )、 Tangent(赤実線 )、 Cosecant(青点線 )、 Secant(緑点線 )、 Cotangent(赤点線 )
単位円上の点の座標の関数であることから、三角関数の間には多数の相互関係が存在する。
三角関数の間に成り立つ最も基本的な恒等式の 1 つとして
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
が挙げられる。これはピタゴラスの基本三角関数公式 (Fundamental Pythagorean trigonometric identity) と呼ばれている[ 8]
上記の式を変形して整理すれば、以下の式が導かれる。
sec
2
θ
−
tan
2
θ
=
1
cos
2
θ
−
tan
2
θ
=
1
,
csc
2
θ
−
cot
2
θ
=
1
sin
2
θ
−
1
tan
2
θ
=
1.
{\displaystyle {\begin{aligned}\sec ^{2}\theta -\tan ^{2}\theta &={\frac {1}{\cos ^{2}\theta }}-\tan ^{2}\theta =1,\\\csc ^{2}\theta -\cot ^{2}\theta &={\frac {1}{\sin ^{2}\theta }}-{\frac {1}{\tan ^{2}\theta }}=1.\end{aligned}}}
負角
sin
(
−
θ
)
=
−
sin
θ
cos
(
−
θ
)
=
cos
θ
tan
(
−
θ
)
=
−
tan
θ
{\displaystyle {\begin{aligned}\sin(-\theta )&=-\sin \theta \\\cos(-\theta )&=\cos \theta \\\tan(-\theta )&=-\tan \theta \end{aligned}}}
余角
sin
(
π
2
−
θ
)
=
cos
θ
cos
(
π
2
−
θ
)
=
sin
θ
tan
(
π
2
−
θ
)
=
cot
θ
{\displaystyle {\begin{aligned}\sin \left({\frac {\pi }{2}}-\theta \right)&=\cos \theta \\\cos \left({\frac {\pi }{2}}-\theta \right)&=\sin \theta \\\tan \left({\frac {\pi }{2}}-\theta \right)&=\cot \theta \end{aligned}}}
補角
sin
(
π
−
θ
)
=
sin
θ
cos
(
π
−
θ
)
=
−
cos
θ
tan
(
π
−
θ
)
=
−
tan
θ
{\displaystyle {\begin{aligned}\sin(\pi -\theta )&=\sin \theta \\\cos(\pi -\theta )&=-\cos \theta \\\tan(\pi -\theta )&=-\tan \theta \end{aligned}}}
sin
(
x
±
y
)
=
sin
x
cos
y
±
cos
x
sin
y
cos
(
x
±
y
)
=
cos
x
cos
y
∓
sin
x
sin
y
tan
(
x
±
y
)
=
tan
x
±
tan
y
1
∓
tan
x
tan
y
{\displaystyle {\begin{aligned}\sin(x\pm y)&=\sin x\cos y\pm \cos x\sin y\\\cos(x\pm y)&=\cos x\cos y\mp \sin x\sin y\\\tan(x\pm y)&={\frac {\tan x\pm \tan y}{1\mp \tan x\tan y}}\end{aligned}}}
三角関数および指数関数は冪級数 によって定義 されているものとすると、負角公式と指数法則およびオイラーの公式 より
1
=
e
0
=
e
i
θ
−
i
θ
=
e
i
θ
e
−
i
θ
=
(
cos
θ
+
i
sin
θ
)
(
cos
θ
−
i
sin
θ
)
=
sin
2
θ
+
cos
2
θ
{\displaystyle {\begin{aligned}1&=e^{0}=e^{i\theta -i\theta }=e^{i\theta }e^{-i\theta }\\&=\left(\cos \theta +i\sin \theta \right)\left(\cos \theta -i\sin \theta \right)\\&=\sin ^{2}\theta +\cos ^{2}\theta \end{aligned}}}
である。
sin および cos については、冪級数による表示から明らかである。また
tan
(
−
θ
)
=
sin
(
−
θ
)
cos
(
−
θ
)
=
−
sin
θ
cos
θ
=
−
tan
θ
{\displaystyle \tan(-\theta )={\frac {\sin(-\theta )}{\cos(-\theta )}}={\frac {-\sin \theta }{\cos \theta }}=-\tan \theta }
である。
オイラーの公式
e
i
z
=
cos
z
+
i
sin
z
{\displaystyle e^{iz}=\cos z+i\sin z}
Euler's formula
と負角の公式から
cos
z
=
e
i
z
+
e
−
i
z
2
,
sin
z
=
e
i
z
−
e
−
i
z
2
i
{\displaystyle \cos z={\frac {e^{iz}+e^{-iz}}{2}},\sin z={\frac {e^{iz}-e^{-iz}}{2i}}}
を得て、指数法則
e
z
+
w
=
e
z
e
w
{\displaystyle e^{z+w}=e^{z}e^{w}}
を用いれば sin, cos の加法定理が得られる。これらから他の三角関数についての加法定理も得られる。
PQ (緑 の線分の長さ)を求める。また、三平方の定理 から加法定理を示す方法が挙げられる。この方法では、円周上の任意の 2 点間の距離を 2 通りの座標系について求めることで、両者が等しいことから加法定理を導く。2 点間の距離を求めるのに三平方の定理を用いる。以下では単位円のみを取り扱うが、円の半径によらずこの方法から加法定理を得ることができる。
単位円の周上に 2 点 P = (cosp , sinp ), Q = (cosq , sinq ) を取る。P と Q を結ぶ線分の長さを PQ として、その 2 乗 PQ2 を 2 通りの方法で求めることを考える(右図も参照)。
P と Q の x 座標の差と y 座標の差から、三平方の定理を用いて PQ2 を求める。
P
Q
2
=
(
cos
p
−
cos
q
)
2
+
(
sin
p
−
sin
q
)
2
=
(
cos
2
p
+
sin
2
p
)
+
(
cos
2
q
+
sin
2
q
)
−
2
(
cos
p
cos
q
+
sin
p
sin
q
)
=
2
−
2
(
cos
p
cos
q
+
sin
p
sin
q
)
.
{\displaystyle {\begin{aligned}\mathrm {PQ} ^{2}&=\left(\cos p-\cos q\right)^{2}+\left(\sin p-\sin q\right)^{2}\\&=\left(\cos ^{2}p+\sin ^{2}p\right)+\left(\cos ^{2}q+\sin ^{2}q\right)-2\left(\cos p\cos q+\sin p\sin q\right)\\&=2-2\left(\cos p\cos q+\sin p\sin q\right).\end{aligned}}}
(1 )
次に Q = (cos0, sin0) = (1, 0) となるような座標系を取り、同様に三平方の定理から PQ2 を求める。この座標系に対する操作は、x 軸および y 軸を角度 q だけ回転させる操作に相当するので、P = (cos(p − q ), sin(p − q )) となる。従って、
P
Q
2
=
(
cos
(
p
−
q
)
−
1
)
2
+
(
sin
(
p
−
q
)
−
0
)
2
=
2
−
2
cos
(
p
−
q
)
{\displaystyle {\begin{aligned}\mathrm {PQ} ^{2}&=\left(\cos(p-q)-1\right)^{2}+\left(\sin(p-q)-0\right)^{2}\\&=2-2\cos(p-q)\end{aligned}}}
(2 )
となる。
(1) (2) cos に関する加法定理が得られる。
cos
p
cos
q
+
sin
p
sin
q
=
cos
(
p
−
q
)
.
{\displaystyle {\begin{aligned}\cos p\cos q+\sin p\sin q=\cos(p-q).\end{aligned}}}
(3 )
三角関数の他の性質 を利用することで、(3) sin の加法定理なども導くことができる。
三角関数の微積分 は、以下の表のとおりである。ただし、これらの結果には様々な(一見同じには見えない)表示が存在し、この表における表示はいくつかの例であることに注意されたい。
なお、以下の表の C は積分定数 、ln(·) は自然対数 である。
f
(
x
)
{\displaystyle f(x)}
微分
f
′
(
x
)
{\displaystyle f'(x)}
不定積分
∫
f
(
x
)
d
x
{\displaystyle \int f(x)\,dx}
sin
x
{\displaystyle \sin x}
cos
x
{\displaystyle \cos x}
−
cos
x
+
C
{\displaystyle -\cos x+C}
cos
x
{\displaystyle \cos x}
−
sin
x
{\displaystyle -\sin x}
sin
x
+
C
{\displaystyle \sin x+C}
tan
x
{\displaystyle \tan x}
sec
2
x
=
1
+
tan
2
x
{\displaystyle \sec ^{2}x=1+\tan ^{2}x}
−
ln
|
cos
x
|
+
C
{\displaystyle -\ln \left|\cos x\right|+C}
cot
x
{\displaystyle \cot x}
−
csc
2
x
=
−
(
1
+
cot
2
x
)
{\displaystyle -\csc ^{2}x=-\left(1+\cot ^{2}x\right)}
ln
|
sin
x
|
+
C
{\displaystyle \ln \left|\sin x\right|+C}
sec
x
{\displaystyle \sec x}
sec
x
tan
x
{\displaystyle \sec x\tan x}
ln
|
sec
x
+
tan
x
|
+
C
=
gd
−
1
x
+
C
{\displaystyle \ln \left|\sec x+\tan x\right|+C=\operatorname {gd} ^{-1}x+C}
csc
x
{\displaystyle \csc x}
−
csc
x
cot
x
{\displaystyle -\csc x\cot x}
−
ln
|
csc
x
+
cot
x
|
+
C
=
ln
|
tan
x
2
|
+
C
{\displaystyle -\ln \left|\csc x+\cot x\right|+C=\ln \left|\tan {\frac {x}{2}}\right|+C}
ただし、gd−1 x はグーデルマン関数 の逆関数 である。(gd-1 x = ln|sec x + tan x | )
三角関数の微分では、次の極限
lim
h
→
0
sin
h
h
=
1
{\displaystyle \lim _{h\to 0}{\frac {\sin h}{h}}=1}
の成立が基本的である。このとき、sinx の導関数 が cosx であることは加法定理から従う(が、後述のようにこれは循環論法であると指摘される)。さらに余角公式 cosx = sin (π / 2 x ) から cosx の導関数は −sinx である。すなわち、sinx は微分方程式 y' ' (x ) + y (x ) = 0特殊解 である。また、他の三角関数の導関数も、上の事実から簡単に導ける。
sinx / x x → 0sinx / x x → 0x ラジアンの扇形の面積を2つの三角形の面積ではさんだり[ 9] [ 10] [ 11] はさみうちの原理 から証明する方法がある。これは一般的な日本の高校 の教科書 [ 12] [ 13] 循環論法 であるため論理が破綻しているという主張がなされることがある[ 14]
単位円板の面積が π であることを自明な概念と考えてしまえば循環論法にはならないが、これはいくつかの決められた公理・定義から論理的演繹のみによって証明されたものだけを正しいと考える現代数学の思想とは相反するものである。循環論法を回避する方法の 1 つは、正弦関数と余弦関数を上述のような無限級数で定義するものである(これは三角関数の標準的な定義の 1 つである。また、この無限級数の収束半径は無限大である(すなわち任意の実数や複素数で収束する))。この定義に基づいて
lim
x
→
0
sin
x
x
=
1
{\displaystyle \lim _{x\to 0}{\frac {\sin \,x}{x}}=1}
を示すことができる。
しかしながら、このように定義された三角関数が、本来持つべき幾何学的な性質を有しているかどうかは全く明らかなことではない。これを確かめるためには、三角関数の諸公式(周期性やピタゴラスの基本三角関数公式等)を証明し、また円周率は、余弦関数の正の最小の零点(つまり、cosx = 0 となる正の最小の値)の存在を示し、その 2 倍と定義する。すると、
x
↦
(
cos
x
,
sin
x
)
{\displaystyle x\mapsto (\cos x,\sin x)}
[0, 2π ) から単位円周への(「反時計まわりの」)全単射 であることを示すことができる。(連続微分可能 な)曲線の長さを積分によって定義すれば、単位円周の長さが 2π であることなどがわかり、上のように定義された三角関数や円周率は、初等幾何での三角関数や円周率の素朴な定義と同じものであることが分かった [ 注釈 1]
三角関数は以下のように無限乗積 として書ける。
sin
π
z
=
π
z
∏
n
=
1
∞
(
1
−
z
2
n
2
)
cos
π
z
=
∏
n
=
1
∞
{
1
−
z
2
(
n
−
1
2
)
2
}
{\displaystyle {\begin{aligned}\sin \pi z&=\pi z\prod _{n=1}^{\infty }{\left(1-{\frac {z^{2}}{n^{2}}}\right)}\\\cos \pi z&=\prod _{n=1}^{\infty }\left\{1-{\frac {z^{2}}{(n-{\frac {1}{2}})^{2}}}\right\}\end{aligned}}}
三角関数は以下のように部分分数 に展開される。
π
cot
π
z
=
lim
N
→
∞
∑
n
=
−
N
N
1
z
+
n
=
1
z
+
∑
n
=
1
∞
2
z
z
2
−
n
2
π
tan
π
z
=
−
lim
N
→
∞
∑
n
=
−
N
N
1
z
+
1
/
2
+
n
=
−
∑
n
=
0
∞
2
z
z
2
−
(
n
+
1
/
2
)
2
π
sin
π
z
=
lim
N
→
∞
∑
n
=
−
N
N
(
−
1
)
n
z
+
n
=
1
z
+
∑
n
=
1
∞
(
−
1
)
n
2
z
z
2
−
n
2
π
cos
π
z
=
lim
N
→
∞
∑
n
=
−
N
N
(
−
1
)
n
z
+
1
/
2
+
n
=
−
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
z
2
−
(
n
+
1
/
2
)
2
{\displaystyle {\begin{aligned}\pi \cot \pi z&=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {1}{z+n}}={\frac {1}{z}}+\sum _{n=1}^{\infty }{\frac {2z}{z^{2}-n^{2}}}\\\pi \tan \pi z&=-\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {1}{z+1/2+n}}=-\sum _{n=0}^{\infty }{\frac {2z}{z^{2}-(n+1/2)^{2}}}\\{\frac {\pi }{\sin \pi z}}&=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {(-1)^{n}}{z+n}}={\frac {1}{z}}+\sum _{n=1}^{\infty }{\frac {(-1)^{n}2z}{z^{2}-n^{2}}}\\{\frac {\pi }{\cos \pi z}}&=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {(-1)^{n}}{z+1/2+n}}=-\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n+1)}{z^{2}-(n+1/2)^{2}}}\end{aligned}}}
三角関数の定義域を適当に制限したものの逆関数 を逆三角関数 (ぎゃくさんかくかんすう、英 : inverse trigonometric function −1 を右肩に付して表す。たとえば逆 正弦関数(ぎゃくせいげんかんすう、英 : inverse sine; インバース・サイン)は sin−1 x などと表す。arcsin, arccos, arctan などの記法もよく用いられる。数値計算などにおいては、これらの逆関数はさらに asin, acos, atan などと書き表される。
x
=
sin
y
⟺
y
=
sin
−
1
x
x
=
cos
y
⟺
y
=
cos
−
1
x
x
=
tan
y
⟺
y
=
tan
−
1
x
x
=
cot
y
⟺
y
=
cot
−
1
x
x
=
sec
y
⟺
y
=
sec
−
1
x
x
=
csc
y
⟺
y
=
csc
−
1
x
{\displaystyle {\begin{aligned}x=\sin y&\iff y=\sin ^{-1}x\\x=\cos y&\iff y=\cos ^{-1}x\\x=\tan y&\iff y=\tan ^{-1}x\\x=\cot y&\iff y=\cot ^{-1}x\\x=\sec y&\iff y=\sec ^{-1}x\\x=\csc y&\iff y=\csc ^{-1}x\end{aligned}}}
である。逆関数は逆数 ではないので注意したい。逆数との混乱を避けるために、逆正弦関数 sin−1 x を arcsinx と書く流儀もある。一般に周期関数の逆関数は多価関数 になるので、通常は逆三角関数を一価連続 なる枝に制限して考えることが多い。たとえば、便宜的に主値
−
π
2
≤
sin
−
1
x
≤
π
2
0
≤
cos
−
1
x
≤
π
−
π
2
<
tan
−
1
x
<
π
2
{\displaystyle {\begin{aligned}-{\frac {\pi }{2}}&\leq \sin ^{-1}x\leq {\frac {\pi }{2}}\\0&\leq \cos ^{-1}x\leq \pi \\-{\frac {\pi }{2}}&<\tan ^{-1}x<{\frac {\pi }{2}}\end{aligned}}}
のように選ぶことが多い。またこのとき、制限があることを強調するために、Sin−1 x , Arcsin x のように頭文字を大文字にした表記がよく用いられる。
exp z , cos z , sin z の級数による定義 から、オイラーの公式 exp (iz ) = cos z + i sin z を導くことができる。この公式から下記の 2 つの等式
exp
(
i
z
)
=
e
i
z
=
cos
z
+
i
sin
z
,
exp
(
−
i
z
)
=
e
−
i
z
=
cos
z
−
i
sin
z
{\displaystyle {\begin{aligned}\exp(iz)&=e^{iz}=\cos z+i\sin z,\\\exp(-iz)&=e^{-iz}=\cos z-i\sin z\end{aligned}}}
が得られるから、これを連立 させて解くことにより、正弦関数・余弦関数の指数関数 を用いた表現が可能となる。すなわち、
cos
z
=
e
i
z
+
e
−
i
z
2
,
sin
z
=
e
i
z
−
e
−
i
z
2
i
{\displaystyle {\begin{aligned}\cos z&={\frac {e^{iz}+e^{-iz}}{2}},\\\sin z&={\frac {e^{iz}-e^{-iz}}{2i}}\end{aligned}}}
が成り立つ。この事実により、級数によらずこの等式をもって複素変数 の正弦・余弦関数の定義とすることもある。また、
cos
(
i
z
)
=
e
−
z
+
e
z
2
=
cosh
z
,
sin
(
i
z
)
=
e
−
z
−
e
z
2
i
=
i
sinh
z
{\displaystyle {\begin{aligned}\cos(iz)&={\frac {e^{-z}+e^{z}}{2}}=\cosh z,\\\sin(iz)&={\frac {e^{-z}-e^{z}}{2i}}=i\sinh z\end{aligned}}}
が成り立つ。ここで cosh z , sinh z は双曲線関数 を表す。この等式は三角関数と双曲線関数の関係式と捉えることもできる。複素数 z を z = x + iy (x , y ∈ R )
cos
z
=
cos
(
x
+
i
y
)
=
cos
x
cosh
y
−
i
sin
x
sinh
y
,
sin
z
=
sin
(
x
+
i
y
)
=
sin
x
cosh
y
+
i
cos
x
sinh
y
{\displaystyle {\begin{aligned}\cos z&=\cos(x+iy)=\cos x\cosh y-i\sin x\sinh y,\\\sin z&=\sin(x+iy)=\sin x\cosh y+i\cos x\sinh y\end{aligned}}}
が成り立つ。
他の三角関数は cscz = 1 / sinz , secz = 1 / cosz , tanz = sinz / cosz , cotz = cosz / sinz によって定義できる。
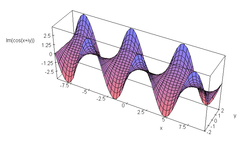
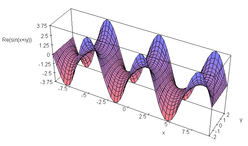
cos(x + iy ) の実部のグラフ
cos(x + iy ) の虚部のグラフ
sin(x + iy ) の実部のグラフ
sin(x + iy ) の虚部のグラフ
球面の三角形 ABC の内角を a , b , c α , β , γ
正弦公式
sina : sinb : sinc = sinα : sinβ : sinγ 余弦公式
cosa = −cosb cosc + sinb sinc cosα 余弦公式
cosα = cosβ cosγ + sinβ sinγ cosa 正弦余弦公式
sina cosβ = cosb sinc − sinb cosc cosα
三角関数の英語の名称の語源について記す。
sineはもとはchord-half(半弦)を意味するサンスクリット語 jya ̄-ardha起源であり、省略形ji ̄va ̄がアラビア語 に音訳されてjibaとなったが、1145年 にチェスターのロバート がフワーリズミー のヒサーブ・アル=ジャブル・ワル=ムカーバラ (英語版 ) ラテン語 に翻訳する際に、jaibと混同した事で胸、湾の意味のsinusと翻訳された[ 17] [ 18]
tangentは”touching”を意味するラテン語tangens由来で、secantは”cutting”を意味するラテン語secans由来である[ 19]
cosine、cotangent、cosecantはそれぞれ接頭辞 のco-がついた形であり、co-はcofunction (英語版 ) compliment angle (英語版 ) 直角三角形 の直角 でないもう一つの角、余角 )に対するsine、tangent、secantという意味である。cosine、cotangentが初めて書かれた形で確認されるのは1620年 のエドマンド・ガンター による”Canon triangulorum”の中である。ラテン語のcosinusとして登場し、これはsinus complementiの略である[ 20]
日本語の正弦、余弦に関しては、徐光啓 らが編纂した『崇禎暦書』の中で、羅雅谷 (英語版 ) 1631年 に著した『測量全義』の八線のうちに見られる[ 21] [ 22] [ 23]
^ 三角関数、円周率、曲線の長さ等の定義の仕方は、複数の流儀がある。
^ a b 山口格「三角関数の研究 」『教授学の探究』第7号、北海道大学教育学部教育方法学研究室、1989年3月、1-23頁、ISSN 0288-3511 、NAID 120000962860 。
^ 内藤, 久資 (1999年). “1999年度後期「Fourier 変換とその応用 ” (PDF). 2014年10月17日 閲覧。 ^ 幡谷泰史; 廣澤史彦. “三角関数と円周率 ” (PDF). 2014年10月7日 閲覧。 ^ 瓜生, 等. “三角関数のさまざまな定義 ” (PDF). 2014年10月8日 閲覧。 ^ Leff, Lawrence S. (2005). PreCalculus the Easy Way ISBN 0-7641-2892-2 . https://books.google.co.jp/books?id=y_7yrqrHTb4C&pg=PA296&redir_esc=y&hl=ja ^ “面積による不等式からの証明 ”. 2015年1月20日 閲覧。 ^ “曲線の長さによる不等式からの証明 ” (PDF). p. 1. 2015年1月20日 閲覧。 ^ 新関章三(元高知大学),矢野 忠(元愛媛大学). “数学・物理通信 ” (PDF). 2015年1月21日 閲覧。 ^ 大矢雅則 、岡部恒治 ほか13名 『新編 数学Ⅲ』(改訂版)数研出版株式会社 、2010年1月10日、53頁。ISBN 978-4-410-80166-2 。 NCID BA89906770 。OCLC 676686067 。 ^ 飯高茂 、松本幸夫 ほか22名『数学Ⅲ』東京書籍株式会社 、2008年2月10日、49頁。ISBN 4-487-15513-4 。 NCID BA71854010 。OCLC 76931848 。 ^ 川中宣明. “循環論法で証明になっていない ” (PDF). p. 1. 2015年1月18日 閲覧。 ^ Victor J. Katz (2008), A History of Mathematics , Boston: Addison-Wesley, 3rd. ed., p. 253, sidebar 8.1. “Archived copy ”. 2015年4月14日時点のオリジナルよりアーカイブ 。2020年12月22日 閲覧。
^ “The Etymology of “Sine” ”. Bill Cherowitzo's Home Page, Mathematical Department, University of Colorado at Denver . December 22, 2020 閲覧。 ^ New Oxford American Dictionary
^ “A reconstruction of Gunter's Canon triangulorum (1620) ”. HAL (2010年12月6日). 2017年7月28日時点のオリジナルよりアーカイブ 。2020年12月22日 閲覧。 ^ 杜石然 (2001). “イエズス会士と西洋数学の伝入” . 中国言語文化研究 1 . https://archives.bukkyo-u.ac.jp/rp-contents/CB/0001/CB00010L001.pdf December 22, 2020 閲覧。
^ 伊達文治 (2015). “三角法と対数の教材に関する史的考察” . 上越数学教育研究 30 . https://www.juen.ac.jp/math/journal/files/vol30/2015-date.pdf December 22, 2020 閲覧。
^ 角川新字源 改訂版 角川学芸出版
Maor, Eli (1998). Trigonometric Delights . Princeton University Press . ISBN 978069105754-5 志賀, 浩二 『数の大航海―対数の誕生と広がり』日本評論社 、1999年7月。ISBN 978-4-535-78289-1 。 高瀬, 正仁 『古典的難問に学ぶ微分積分』共立出版 、2013年7月。ISBN 978-4-320-11041-0 。 Vinogradov, Ivan Matveyevich (2004-09-10). The Method of Trigonometrical Sums in the Theory of Numbers (revised ed.). Dover. ISBN 978-048643878-8 黒川, 信重 、小山, 信也 『多重三角関数論講義』日本評論社 、2010年11月8日。ISBN 978-4-535-785557 。 杉浦, 光夫 『解析入門I』東京大学出版会 〈基礎数学2〉、1980年。ISBN 978-4-13-062005-5 。 黒田, 成俊 『微分積分』共立出版〈共立講座21世紀の数学 第1巻〉、2002年。ISBN 978-4320015531 。 高木, 貞治 『定本 解析概論』(改訂第3版)岩波書店、2010年。ISBN 978-4000052092 。 小平, 邦彦 『解析入門I』(軽装版)岩波書店、2003年。ISBN 978-4000051927 。