Wikipedia:秀逸ピックアップ/ロジスティック写像
表示
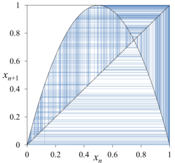
ロジスティック写像とは、xn+1 = axn(1 − xn) という2次関数の差分方程式(漸化式)で定められた離散力学系である。単純な2次関数の式でありながら、驚くような複雑な振る舞いが生み出される。特に数理生物学者ロバート・メイの研究によってロジスティック写像は広く知られるようになり、生物の個体数の変化を表すモデルとしても知られる。
適当にパラメータ a の値を決め、最初の変数 x0 を決めて計算すると、x0, x1, x2, … という軌道が得られる。a を変化させると、ロジスティック写像の軌道は、一つの値へ落ち着いたり、いくつかの値を周期的に繰り返したり、カオスと呼ばれる非周期的変動を示したりと様々に変化する……
