2元消失通信路

2元消失通信路のモデル。消失確率は P

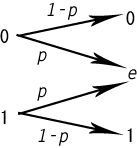
2元消失通信路（英: Binary Erasure Channel、BEC）とは、符号理論および情報理論で使われる典型的な伝送路モデルの1つである。このモデルでは、送信側が0または1のビットを送信したとき、受信側はそのビットを受信する可能性もあるし、そのビットを含まない（消失した）メッセージを受信する可能性もある。解析が容易であるため、情報理論でよく使われる。

概要

BECは2元通信路である。すなわち、2種類のシンボルだけを送ることができ、通常、0と1で表す（2元でない通信路では、2種類以上のシンボル、場合によっては無限種類のシンボルを送ることができる）。この通信路は完全ではなく、ビットが消失することがある。すなわち、ビットが変化してしまい、受信側がそのシンボルを識別できない場合がある。

BECでは、ある意味で誤りが存在しない。2元対称通信路とは異なり、受信できたビットは常に正しい。問題はビットが消失した場合である。

この通信路は、ノイズのある通信路を単純化したものであるため、理論の研究によく使われる。通信理論における多くの問題はBECに還元可能である。

定義

消失確率 p の2元消失通信路は、2元入力/3元出力の通信路で、消失する確率が p である。X を {0, 1} というアルファベットの送信側確率変数であるとする。また、Y を {0, 1, e} というアルファベットの受信側確率変数であるとする。ここで、e は消失シンボルである。すると、この通信路の特性は以下のように条件付き確率で表される。

Pr( Y = 0 | X = 0) = 1-p

Pr( Y = e | X = 0) = p

Pr( Y = 1 | X = 0) = 0

Pr( Y = 0 | X = 1) = 0

Pr( Y = e | X = 1) = p

Pr( Y = 1 | X = 1) = 1-p

BEC の通信路容量

BEC の通信路容量は 1 - p である。

直観的には 1 - p は、この通信路の通信路容量の上限と見ることができる。全能の精霊がビットが消失した場合に常にそれを知らせてくれるとする。情報源はビットの消失を防ぐことはできないが、それが起きたら対処することができる。例えば、ビットが受信されるまで、同じビットを繰り返し送信することができる。この場合、X は符号化される必要は無く、Y は受信したビットが X が送ろうとしていたビットであるとみなすことができる。従って、精霊の存在を前提とすれば、転送レートの平均は 1 - p となる。しかし、そのような精霊は存在しないので、1 - p は通信路容量の上限となる。

関連項目

• 2元対称通信路

参考文献

• David J. C. MacKay. Information Theory, Inference, and Learning Algorithms Cambridge: Cambridge University Press, 2003. ISBN 0-521-64298-1
• Thomas M. Cover, Joy A. Thomas. Elements of information theory, 1st Edition. New York: Wiley-Interscience, 1991. ISBN 0-471-06259-6.