黄金比音律

36平均律表記での833セントのスケール。スラーは黄金比の関係になっているもの。

黄金比音律(おうごんひおんりつ)または833セントスケールは、833.09セントの音程の組み合わせで構成される音律であり、フィボナッチ数列に基づく^[1]。黄金比は $\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.6180339887\ldots .$ であり、この比を音程に換算すると833.09セント（ Play^{[ヘルプ/ファイル]}）に相当する。

導出

任意の2つの音高を選び、その高い方の音と選んだ音程の結合音で新たな音程を取る。次に、その音程で同じことを行う。これを繰り返すことで音程が833セントに近い値に収束する^[1]。

基本音程	最も近い組み合わせトーン（比率）	最も近い組み合わせトーン（セント）
2：1	3：2	701.955
3：2	5：3	884.359
5：3	8：5	813.686
8：5	13：8	840.528
13：8	21:13	830.253
21:13	34:21	834.175
34:21	55:34	832.676
55:34	89:55	833.248
89:55	144：89	833.030
144：89	233：144	833.113
233：144	377：233	833.081
377：233	610：377	833.094
...

例えば、 220 Hzと220 Hzのユニゾンからは0 Hz（差音）と440 Hz（加音）の結合音が得られる。440 Hzは220 Hzの1オクターブ上の音である。続いて、220 Hzと440 Hzの加音は660 Hzの結合音であり、440 Hzの完全五度（3：2）上の音である。さらに、440 Hzと660 Hzから1,100 Hzの加音が得られ、1,100 Hzと660 Hzは長六度（5：3）の関係にある。同様にして1,760 Hzの加音を得て、1,100 Hzと短六度（8：5）の関係になっている。どの音程から開始しても常に833セントに収束する^[1]。

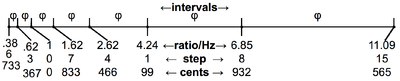
833.09セントの間隔が決定されると、それらのスタックが生成される。

トーン	−5	−4	−3	−2	-1	0	1	2	3	4	5
セント	634.55	267.64	1100.73	733.82	366.91	0	833.09	466.18	99.27	932.36	565.45
比率	1.443	1.167	1.889	1.528	1.236	1.000	1.618	1.309	1.059	1.713	1.386
スケールステップ				6	3	0	7	4	1	8	15

黄金比が無理数であることを考えると、正確なユニゾンまたはオクターブに戻ることはない。

黄金比音階

Bohlenは、黄金比音程から対称的な七音音階として黄金比音階を記述している Play^{[ヘルプ/ファイル]}。

スケールステップ	0		1		2		3		4		5		6		7		...
セント	00.00		99.27		235.77		366.91		466.18		597.32		733.82		833.09		...
ステップ幅		99.27		136.5		131.14		99.27		131.14		136.5		99.27		...
積み上げ $\varphi$ トーン	0		3				-1		2				−2		1		...

この構成の仕方は、五度圏上の積み重ね（FCGDAEB = CDEFGAB）による長音階の導出に相当する。

ステップ	比	周波数比	セント	セント幅	音声
0	$\varphi$ ⁄ $\varphi$	1.0000	0		Play
0	$\varphi$ ⁄ $\varphi$	1.0000	0	99.27	Play
1	$\varphi$ ⁴⁄4 $\varphi$	1.0590	99.27	99.27	Play
1	$\varphi$ ⁴⁄4 $\varphi$	1.0590	99.27	136.50	Play
2	3 $\varphi$ ⁄ $\varphi$ ³	1.1459	235.77	136.50	Play
2	3 $\varphi$ ⁄ $\varphi$ ³	1.1459	235.77	131.14	Play
3	2 $\varphi$ ⁄ $\varphi$ ²	1.2361	366.91	131.14	Play
3	2 $\varphi$ ⁄ $\varphi$ ²	1.2361	366.91	99.27	Play
4	$\varphi$ ³⁄2 $\varphi$	1.3090	466.18	99.27	Play
4	$\varphi$ ³⁄2 $\varphi$	1.3090	466.18	131.14	Play
5	⁄_3/³	1.4120	597.32	131.14	Play
5	⁄_3/³	1.4120	597.32	136.50	Play
6	4 $\varphi$ ⁄ $\varphi$ ³	1.5279	733.82	136.50	Play
6	4 $\varphi$ ⁄ $\varphi$ ³	1.5279	733.82	99.27	Play
7 (0)	$\varphi$ ²⁄ $\varphi$	1.6180	833.09	99.27	Play
7 (0)	$\varphi$ ²⁄ $\varphi$	1.6180	833.09	99.27	Play
8 (1)	$\varphi$ ⁵⁄4 $\varphi$	1.7135	932.36	99.27	Play
8 (1)	$\varphi$ ⁵⁄4 $\varphi$	1.7135	932.36	136.50	Play
9 (2)	3 $\varphi$ ⁄ $\varphi$ ²	1.8541	1,068.86	136.50	Play
9 (2)	3 $\varphi$ ⁄ $\varphi$ ²	1.8541	1,068.86	131.14	Play
10 (3)	$\varphi$ ⁄ $\varphi$	1.0000	0	131.14	Play
10 (3)	$\varphi$ ⁄ $\varphi$	1.0000	0	99.27	Play
11 (4)	$\varphi$ ⁴⁄4 $\varphi$	1.0590	99.27	99.27	Play
11 (4)	$\varphi$ ⁴⁄4 $\varphi$	1.0590	99.27	131.14	Play
12 (5)	$\varphi$ ⁄6 $\varphi$ / $\varphi$ ⁴	1.1424	230.41	131.14	Play
12 (5)	$\varphi$ ⁄6 $\varphi$ / $\varphi$ ⁴	1.1424	230.41	136.50	Play
13 (6)	2 $\varphi$ ⁄ $\varphi$ ²	1.2361	366.91	136.50	Play
13 (6)	2 $\varphi$ ⁄ $\varphi$ ²	1.2361	366.91	99.27	Play
14 (0)	$\varphi$ ³⁄2 $\varphi$	1.3090	466.18	99.27	Play
14 (0)	$\varphi$ ³⁄2 $\varphi$	1.3090	466.18	99.27	Play
15 (1)	$\varphi$ ⁶⁄8 $\varphi$	1.3863	565.45	99.27	Play
15 (1)	$\varphi$ ⁶⁄8 $\varphi$	1.3863	565.45	136.50	Play
16 (2)	3 $\varphi$ ⁄2 $\varphi$	1.5	701.96	136.50	Play
16 (2)	3 $\varphi$ ⁄2 $\varphi$	1.5	701.96		Play
...

黄金比音階には、1オクターブあたり0.83333×12ステップ（約10ステップ）が含まれる^[2]。また、黄金比音律は36平均律を用いることで近似でき、この近似においては36平均律に12平均律が内包されているという利点がある^[3]。

脚注

^ ^a ^b ^c Bohlen, Heinz (last updated 2012). "An 833 Cents Scale: An experiment on harmony", Huygens-Fokker.org.
^ Pareyon, Gabriel (2011). On Musical Self-Similarity, p.398. ISBN 9789525431322.
^ "833 Cent Golden Scale (Bohlen)", Xenharmonic Wiki.

外部リンク

"Fun with Emulator X: Bohlen 833 cents scale and harmonics", CatSynth.
"Golden Ratio", Xenharmonic Wiki.

この項目は、音楽に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（ポータル音楽/ウィキプロジェクト音楽）。

[Experiment-1] Bohlen, Heinz (last updated 2012). "An 833 Cents Scale: An experiment on harmony", Huygens-Fokker.org.

[Self-Similarity-2] Pareyon, Gabriel (2011). On Musical Self-Similarity, p.398. ISBN 9789525431322.

[Xen-3] "833 Cent Golden Scale (Bohlen)", Xenharmonic Wiki.

[1]

[2]

[3]

導出

黄金比音階

関連項目

脚注

外部リンク