関係の圏

関係圏 Rel

反対圏 Rel^op

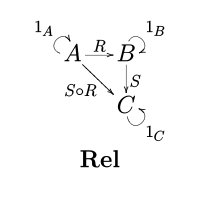
数学の一分野である圏論において関係の圏（かんけいのけん、英: category of relations）Rel は、すべての集合を対象とし、すべての二項関係を射とする圏である。

この圏における射 R: A → B が A, B 間の関係であるというのは、 R ⊆ A × B であることを意味する。

二つの関係 R: A → B, S: B → C の合成は

(a, c) ∈ S ∘ R ⇔ ∃b ∈ B s.t. (a, b) ∈ R かつ (b, c) ∈ S

で与えられる。

性質

• 関係の圏 Rel は集合の圏 Set を（ワイドな）部分圏として含む。ただし、Set における射（つまり写像）f: X → Y は付随する函数関係 F ⊆ X × Y ((x, y) ∈ F ⇔ f(x) = y) に対応する。
• 関係の圏 Rel は、冪集合をとる操作を共変函手と見なしたものに対応する函手をもつモナドに対するクライスリ圏として、集合の圏 Set から得られる。
• 初見では呑み込みづらいと思われる事実に、関係の圏 Rel における圏論的直積が（Set の直積が集合論的直積であるのと違って）集合論的直和によって与えられることが挙げられる。それはまた圏論的直和でもある。
• 関係の圏 Rel はモノイド閉圏を成す。ただし、モノイド積 A ⊗ B および内部射 A ⇒ B はともに集合のデカルト積で与えられる。
• 関係 R の逆 R⁻¹（(b, a) ∈ R⁻¹: B → A ⇔ (a, b) ∈ R: A → B）をとる対合的操作は、対象をそのままに射とその合成順を逆にする反変函手 Rel^op → Rel を誘導する。これにより関係の圏 Rel はダガー圏となる。実は Rel はダガーコンパクト圏である。

関連項目

• 寓 (圏論): 関係の圏は寓の模範例である

外部リンク

• Rel in nLab
• bicategory of relations in nLab