「ガラス特性の計算」の版間の差分
編集の要約なし |
m 曖昧さ回避ページ最適化へのリンクを解消、リンク先を数理最適化に変更(DisamAssist使用) |
||
| (8人の利用者による、間の9版が非表示) | |||
| 1行目: | 1行目: | ||
[[Image:Spidergraph Refractive Index.GIF|250px|サムネイル|ガラスの特性計算は求める物性の「微調整」を可能にする。この例は[[屈折率]]。<ref>[http://glassproperties.com/refractive_index/ Calculation of the Refractive Index of Glasses]</ref>]] |
|||
{{翻訳依頼|date=2016年4月24日 (日) 02:42 (UTC)}} |
|||
'''ガラス特性の計算'''(ガラスとくせいのけいさん、'''ガラスのモデル化''')は、関心のもたれる[[ガラス]]の物性や、特定条件下(たとえば製造工程)でのガラスの挙動を、時間、材料、経済的・環境的資源を節約するため、過去のデータと経験に基づく実験的研究を行うことなく予測するために利用される。19世紀の末にA. Winkelmannと[[フリードリッヒ・オットー・ショット]]によって初めて行われた。[[数理最適化|最適化]]と[[シックス・シグマ]]手法のために、いくつかのガラスモデルとこれらに関係する計算式を組み合わせて使うことができる。[[統計学|統計的分析]]の形でガラスのモデル化は、新しいデータ、実験手順、測定機関(ガラス研究施設)の評価・認定を支援することができる。 |
|||
== 歴史 == |
== 歴史 == |
||
歴史的に、ガラス特性の計算はガラス科学の創始と直接関係している。19世紀の末に、物理学者[[エルンスト・アッベ]]は[[ドイツ]]の[[イェーナ]]で[[カール・フリードリヒ・ツァイス|カール・ツァイス]]の光学工場との共同作業に刺激され、最適化された[[光学顕微鏡]]の設計計算ができる数式を導いた。アッベ以前、顕微鏡は工芸品であり、組み立ては熟練した職人によっていたので、光学顕微鏡は非常に高価であり、品質にもばらつきがあった。アッベはどのように最高の顕微鏡を組み立てればよいかが分かったが、これに必要な特定の[[屈折率]]と[[分散 (光学)|分散]]を持つ[[レンズ]]と[[プリズム]]は存在していなかった。アッベはガラス工芸家や技術者からは答えを得ることができなかった。この時代のガラス作りは科学に基づいたものではなかった。<ref name=vogel>{{cite book |author=Vogel, Werner |title=Glass chemistry |publisher=Springer-Verlag |location=Berlin |year=1994 |isbn=3-540-57572-3 |edition=2nd revised }}</ref> |
|||
| ⚫ | |||
1879年、ガラス技術者[[フリードリッヒ・オットー・ショット|オットー・ショット]]は、特別な光学的性質を期待して自分で作成した特殊な配合のガラス試料(ケイ酸リチウムガラス)をアッベに送った。アッベの測定によると、ショットのガラスは期待した特性ではなかった。にもかかわらず、アッベはこの問題をさらに研究し、すべてのガラス成分を系統的に評価するようにショットを招いた。最終的に、ショットは均質なガラスの試料を作ることに成功し、アッベが望んでいた光学特性を持つ[[ホウケイ酸ガラス]]を発明した。<ref name=vogel/>これらの発明が有名な[[カール・ツァイス]]と[[ショット (ガラス製造業)|ショット社]]を興す基になった({{仮リンク|顕微鏡技術の年表|en|Timeline of microscope technology}}を参照)。系統的なガラス研究がここに始まった。1908年、Eugene Sullivan もアメリカでガラスの研究を開始した([[コーニング (企業)|コーニング]]、[[ニューヨーク州]])。<ref>[http://www.corning.com/inside_corning/our_heritage.aspx Eugene Sullivan and Corning Glass Works]</ref> |
|||
ガラス研究の初期には、ガラスの組成と特性との関係を知ることが最も重要であった。この目的のため、ショットはいくつかの書物でガラス特性の計算に{{訳語疑問点範囲|'''加法則'''|2018年2月}}を導入した。<ref>{{cite journal |author1=Winkelmann A. |author2=Schott O. |title=Über die Elastizität und über die Druckfestigkeit verschiedener neuer Gläser in ihrer Abhängigkeit von der chemischen Zusammensetzung |journal=Annalen der Physik und Chemie |volume=51 |pages=697 |year=1894}}</ref><ref>{{cite journal |author1=Winkelmann A. |author2=Schott O. |title=Über thermische Widerstandscoefficienten verschiedener Gläser in ihrer Abhängigkeit von der chemischen Zusammensetzung |journal=Annalen der Physik und Chemie |volume=51 |issue= |pages=730 |year=1894 |doi=10.1002/andp.18942870407|bibcode = 1894AnP...287..730W }}</ref><ref>{{cite journal |author1=Winkelmann A. |author2=Schott O. |title=Über die specifischen Wärmen verschieden zusammengesetzter Gläser |journal=Annalen der Physik und Chemie |volume=49 |page=401 |year=1893 |doi=10.1002/andp.18932850702|bibcode = 1893AnP...285..401W }}</ref>この原理は、ガラスの組成と特定の物性がすべての成分の濃度と線形であることを暗示しており、下の式で C<sub>i</sub> と b<sub>i</sub> がそれぞれ理想的なガラス成分とそれに対応する係数となる[[理想溶液|理想混合物]]を仮定している。加法則は単純化であり、[[屈折率]]と[[粘度]]のグラフに見られるように、狭い組成範囲でのみ有効である。にもかかわらず、[[光学ガラス]]、調理や研究に使われる[[ホウケイ酸ガラス|低熱膨張ガラス]](Pylex、Duranなど)、水銀[[温度計]]用に[[凝固点降下]]の小さいガラスなど、ショット社の発明の多くに加法則が使われている。その後、English<ref>{{cite journal |author=English S. |title=The effect of composition on the viscosity of glass. Part II |journal=J. Soc. Glass Technol. |volume=8 |pages=205–48 |year=1924 }}<br/>{{cite journal |title=... Part III Some Four-component Glasses |journal=J. Soc. Glass Technol. |volume=9 |pages=83–98 |year=1925 }}<br/>{{cite journal |title=...Part IV. Calculation of the Influence of Minor Constituents |journal=J. Soc. Glass Technol. |volume=10 |pages=52–66 |year=1926 }}</ref>と Gehlhoff et al.<ref>{{cite journal |author1=Gehlhoff G. |author2=Thomas M. |journal=Z. Tech. Phys. |issue=6 |page=544 |year=1925}}; {{cite journal |journal=Z. Tech. Phys. |issue=7 |pages=105, 260 |year=1926}}; "Lehrbuch der technischen Physik", J. A. Barth-Verlag, Leipzig, 1924, p 376.</ref>が同様に加法的なガラスの特性計算モデルを発表した。ショットの加法則は今日でもガラスの研究開発に広く使われている。<ref>{{cite journal |author1=Lakatos T. |author2=Johansson L.G. |author3=Simmingsköld B. |title=Viscosity temperature relations in the glass system SiO<sub>2</sub>-Al<sub>2</sub>O<sub>3</sub>-Na<sub>2</sub>O-K<sub>2</sub>O-CaO-MgO in the composition range of technical glasses |journal=Glass Technology |volume=13 |issue=3 |pages=88–95 |date=June 1972 }}</ref><ref>{{cite book |author1=Terese Vascott |author2=Thomas P. Seward III |title=High Temperature Glass Melt Property Database for Process Modeling |publisher=Wiley-American Ceramic Society |year=2005 |isbn=1-57498-225-7 }}</ref> |
|||
:'''加法則:''' <math>\mbox{Glass Property} = b_0 + \sum_{i=1}^n b_iC_i</math> |
|||
== グローバルモデル == |
|||
[[Image:Mixed-Alkali Effect Viscosity.GIF|250px|thumb|[[混合アルカリ効果]]: ガラスが2つ以上の[[アルカリ金属]]酸化物を含む場合、いくつかの物性は加法性を示さない。図では[[粘度]]が著しく低下している。<ref>[http://glassproperties.com/viscosity/mixed-alkali-effect-viscosity/ The Mixed-Alkali Effect for the Viscosity of Glasses]</ref>]] |
|||
[[Image:Measurement Error Development.gif|250px|thumb|SiO<sub>2</sub>-Na<sub>2</sub>O 二成分系における20℃での[[密度]]について、近年のガラス文献におる[[正確度]]の低下<ref name=errors>[http://glassproperties.com/errors/ Overview, Measurement Errors of Glass Properties]</ref>]] |
|||
その後、ショットと多くの科学者・技術者たちは、十分狭い組成範囲について、自分たちの研究所で測定された実験値を加法則にあてはめた('''ローカルガラスモデル''')。研究所間の不一致や、非線形なガラス成分の作用を考える必要がないため、これは大変便利だった。数十年にわたる系統的なガラス研究の進行により、何千種類のガラス組成が研究された結果、何百万のガラス特性が発表され、{{仮リンク|ガラスデータベース|en|Glass databases}}に集められた。この膨大な実験データの集積は、Bottinga<ref>{{cite journal |doi=10.2475/ajs.272.5.438 |author1=Bottinga Y. |author2=Weill D.F. |title=The viscosity of magmatic silicate liquids: a model for calculation |journal=Am. J. Sci. |volume=272 |pages=438–75 |date=May 1972 |issue=5}}</ref>、 Kucuk<ref>{{cite journal |author1=Kucuk A. |author2=Clare A. G |author3=Jones L. |title=An estimation of the surface tension of silicate glass melts at 1400 °C using statistical analysis |journal=Glass Technol. |volume=40 |issue=5 |pages=149–53 |date=October 1999}}</ref>、 Priven<ref>{{cite journal |author=Priven A.I. |title=General Method for Calculating the Properties of Oxide Glasses and Glass-Forming Melts from their Composition and Temperature |journal=Glass Technology |volume=45 |issue=6 |pages=244–54 |date=December 2004 |url=http://www.sciglass.info/Publications/Priven.pdf}}</ref>、 Choudhary<ref>{{cite book |author1=M. K. Choudhary |author2=R. M. Potter |chapter=9. Heat Transfer in Glass-Forming Melts |chapterurl=https://books.google.com/books?id=oFs1ImozZW4C&pg=PA249 |editor1=Angelo Montenero |editor2=Pye, David |editor3=Innocent Joseph |title=Properties of Glass-Forming Melts |publisher=CRC |location=Boca Raton |year=2005 |isbn=1-57444-662-2 }}</ref>、 Mazurin<ref>O. V. Mazurin, O. A. Prokhorenko: [https://books.google.com/books?id=oFs1ImozZW4C&pg=PA295 "Electrical conductivity of glass melts"]; Chapter 10 in: "Properties of Glass-Forming Melts" ed. by D. L. Pye, I. Joseph, A. Montenaro; CRC Press, Boca Raton, Florida, 2005, {{ISBN2|1-57444-662-2}}.</ref>、 Fluegel<ref>{{cite journal |author=Fluegel A. |title=Glass Viscosity Calculation Based on a Global Statistical Modeling Approach |journal=Glass Technol.: Europ. J. Glass Sci. Technol. A |volume=48 |issue=1 |pages=13–30 |year=2007 |url=http://glassproperties.com/viscosity/Viscosity_2006_AFluegel.pdf |format=PDF}}</ref><ref>{{cite journal|doi=10.1111/j.1551-2916.2007.01751.x|title=Global Model for Calculating Room-Temperature Glass Density from the Composition|year=2007|last1=Fluegel|first1=Alexander|journal=Journal of the American Ceramic Society|volume=90|pages=2622|issue=8}}</ref>が様々なアプローチによる'''グローバルガラスモデル'''を発表するまで全体としての研究がされていなかった。ショットのモデルとは対照的に、グローバルガラスモデルは多くの独立したデータ源を考慮しており、モデルによる推定はより確からしいものになっている。グローバルガラスモデルはさらに、右図に見られる[[混合アルカリ効果]]や{{訳語疑問点範囲|ホウ素特例|2018年2月}}のように、特定のガラス成分の組み合わせが特性に及ぼす非線形効果を明らかにし定量化した。グローバルガラスモデルはまた、ガラス特性測定の[[正確度]]の興味深い発達を反映している。たとえば、図示したように現代の科学文献におけるいくつかのガラス特性の実験データの正確度の低下である。これらは、新しいデータ、測定手順、測定機関(ガラス研究施設)の評価・認定に利用することができる。以下の節では、([[融解熱]]を除いて)膨大な実験データをうまく扱えるように見える経験的なモデル化手法を述べる。得られるモデルは今日の工業的応用やガラスの特性計算の研究に利用されている。 |
|||
非経験的([[演繹]]的)ガラスモデルも存在する。<ref>Milos B. Volf: "Mathematical Approach to Glass" Glass Science and Technology, vol. 9, Elsevier, 1988, {{ISBN2|0-444-98951-X}}</ref>それらはそもそもガラス特性の確かな予測を得るためでなく、しばしばいくつかの特性([[原子半径]]、[[原子量]]、[[化学結合]]の[[結合エネルギー|強さ]]と[[結合角]]、[[原子価|結合の価数]]、[[比熱]])の間の関係を確立して科学的な洞察を得るために作られたものである。将来的には、諸特性間の関係が十分に理解され、必要なすべての実験データが利用可能であれば、演繹的モデルにおける特性間の関係の研究により、最終的には求める特性すべてについて精度の高い予測が導かれる可能性がある。 |
|||
== 手法 == |
|||
ガラスの特性と製造中の挙動は、GE-SYSTEM<ref name="GE-SYSTEM">[http://www.smartdata.cn/en/ges2010/index.html GE-SYSTEM]</ref>、SciGlass<ref>[http://www.sciglass.info/ SciGlass] {{webarchive|url=https://web.archive.org/web/20071016044859/http://www.sciglass.info/ |date=2007-10-16 }}</ref>、 Interglad<ref>[http://www.newglass.jp/interglad_n/gaiyo/info_e.html Interglad]</ref>のようなガラスデータベースの統計的な分析により、時には[[有限要素法]]と結びつけることで、計算することができる。[[融解熱]]の見積もりには[[熱力学データベース]]を用いる。 |
|||
=== 線形回帰 === |
|||
[[Image:refractive index SiO2 Na2O.gif|250px|thumb|SiO<sub title="屈折率" href="屈折率">2</sub>-Na<sub title="ダミー変数" href="ダミー変数">2</sub>O 系における[[屈折率]]。1人の研究者からのデータ系列全体の系統的な差異を定量化するために、[[ダミー変数]]を使うことができる。<ref name=errors/>]] |
|||
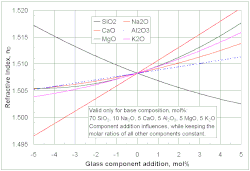
求めたいガラス特性が[[結晶化]]や[[相分離]]に関係がない場合(たとえば[[液相線温度]])、3次までの{{訳語疑問点範囲|一般化[[多項式]]|2018年2月}}を使った[[線形回帰]]を利用できる。下は2次式の例である。C は%またはその他の単位による[[酸化ナトリウム|Na<sub>2</sub>O]]や[[酸化カルシウム|CaO]]のようなガラス成分の濃度、b は係数、n はガラス成分の数である。すべての成分を合計すると100%になるため変数が過剰になるので、ガラスの主成分である[[シリカ]](SiO<sub>2</sub>)は下の式からはずす。下式の多くの項は[[相関]]と[[有意性]]の分析に基づいて無視することができる。図に見られるような[[系統誤差]]は[[ダミー変数]]によって定量化される。さらなる詳細とその他の例はFluegel<ref>A. Fluegel: [http://glassproperties.com/principle/Statistics_Glass_2007.pdf Statistical Regression Modeling of Glass Properties - A Tutorial]</ref>のオンライン・チュートリアルで見ることができる。 |
|||
| ⚫ | |||
=== 非線形回帰 === |
|||
[[Image:TL-SiO2-Na2O-CaO.gif|250px|thumb|28研究者による237組の実験データに基づく離散的なピーク関数を用いたSiO<sub id="cite_ref-liquidus_25-0">2</sub>-Na<sub>2</sub>O-CaO系の液相面。誤差=15℃。<ref name=liquidus>[http://glassproperties.com/liquidus/ Glass Liquidus Temperature Calculation using disconnected peak functions]</ref>]] |
|||
[[液相線温度]]は[[ニューラルネットワーク]]<ref>{{cite journal|doi=10.1016/S0022-3093(02)01859-8|title=A machine learning approach to the estimation of the liquidus temperature of glass-forming oxide blends|year=2003|last1=Dreyfus|first1=C|journal=Journal of Non-Crystalline Solids|volume=318|pages=63|bibcode = 2003JNCS..318...63D }}</ref>と離散的な[[ピーク関数]]を用いた[[非直線回帰]]によってモデル化されている。<ref name=liquidus/>離散的なピーク関数のアプローチは、1つの[[初晶領域]]の中では[[線形回帰]]が適用でき<ref>{{cite journal |author1=Hanni J.B. |author2=Pressly E. |author3=Crum J.V. |author4=Minister K.B.C. |author5=Tran D. |author6=Hrma P. |author7=Vienna J.D. |title=Liquidus temperature measurements for modeling oxide glass systems relevant to nuclear waste vitrification |journal=Journal of Materials Science |volume=20 |issue=12 |pages=3346–57 |year=2005 |doi=10.1557/JMR.2005.0424|bibcode = 2005JMatR..20.3346H }}</ref>、[[共晶点]]で突然に変化が起こるという観測に基づいている。 |
|||
=== ガラスの融解熱 === |
|||
ガラスの[[融解熱]]は、原料の混合物(バッチ)を溶融ガラスにするために必要なエネルギーの量を反映する。これは、バッチおよびガラスの組成、[[炉]]および[[廃熱回収]]システムの効率、ガラスの炉内滞留時間の平均、その他の多くの因子に依存する。Carl Krögerが1953年にこの問題についての先駆的な論文を書いた。<ref>{{cite journal |author=Kröger, Carl |title=Theoretischer Wärmebedarf der Glasschmelzprozesse (Theoretical heat demand of glass melting processes) |journal=Glastechnische Berichte |volume=26 |issue=7 |pages=202–14 |year=1953 |language=German}}</ref> |
|||
=== 有限要素法 === |
|||
[[ガラス溶融炉]]内のガラスの流れをモデル化するために、溶融ガラスの[[粘度]]、[[密度]]、[[熱伝導率]]、[[比熱]]、[[吸収スペクトル]]、その他の関連する特性についてのデータまたはモデルに基づいて、[[有限要素法]]が商業的に応用されている。<ref>[http://www.gsl.cz/en/products/furnace-design.html Glass Service, Furnace Design]</ref><ref>Brochure: [http://www.fluent.com/solutions/brochures/glass.pdf Flow modeling software for the glass industry], Fluent Inc.</ref> 有限要素法はまた、ガラスの成形工程にも応用されることがある。 |
|||
=== 複数の特性の最適化 === |
|||
[[生産コスト]]を含め、いくつかのガラス特性を同時に[[数理最適化|最適化]]することがしばしば要求される。<ref name="GE-SYSTEM"/><ref>[http://glassproperties.com/optimization/ Glass property optimization]</ref> これは次のように[[シンプレックス法]]または[[表計算ソフト]]で行うことができる。 |
|||
# 求める特性の一覧を作成する。 |
|||
# 信頼性をもって組成に基づいたガラスの特性計算ができるように、モデルを入力する。生産コストを見積もる計算式を含む。 |
|||
# 望む特性と計算された特性との間の差([[誤差]])の2乗を計算する。 |
|||
# ガラス成分を変数として誤差の2乗の合計([[残差平方和]])を減らす。例えばMicrosoft Excelのソルバーオプション<ref>[http://www.solver.com/suppstdsolver.htm Excel Solver]</ref> を使用する。最適化に他のソフト(例えば[[Origin (グラフ作成ソフト)|Origin]])を使うこともできる。 |
|||
望む特性ごとに異なる重みをつけることもできる。原理についての基本的な情報はHuff et al.<ref>{{cite journal|doi=10.1111/j.1151-2916.1973.tb12356.x|title=Computerized Prediction of Glass Compositions from Properties|year=1973|last1=Huff|first1=N. T.|last2=Call|first2=A. D.|journal=Journal of the American Ceramic Society|volume=56|pages=55|issue=2}}</ref>の論文に見られる。いくつかのガラスモデルの組み合わせに、さらに関連する技術的および財務的関数を加えたものは、[[シックス・シグマ]]の最適化に使うことができる。 |
|||
== 関連項目 == |
== 関連項目 == |
||
* |
*{{仮リンク|ガラスのバッチ計算|en|Glass batch calculation}} |
||
*[[ガラス]] |
|||
*[[相図|相平衡状態図]] |
|||
== |
== 脚注 == |
||
{{ |
{{reflist|30em}} |
||
{{デフォルトソート:からすとくせい}} |
{{デフォルトソート:からすとくせいのけいさん}} |
||
[[カテゴリ:ガラス]] |
|||
| ⚫ | |||
[[ |
[[カテゴリ:アモルファス]] |
||
[[カテゴリ:物性物理学]] |
|||
[[カテゴリ:材料工学]] |
|||
| ⚫ | |||
[[カテゴリ:相転移]] |
|||
2023年9月17日 (日) 14:55時点における最新版
ガラス特性の計算(ガラスとくせいのけいさん、ガラスのモデル化)は、関心のもたれるガラスの物性や、特定条件下(たとえば製造工程)でのガラスの挙動を、時間、材料、経済的・環境的資源を節約するため、過去のデータと経験に基づく実験的研究を行うことなく予測するために利用される。19世紀の末にA. Winkelmannとフリードリッヒ・オットー・ショットによって初めて行われた。最適化とシックス・シグマ手法のために、いくつかのガラスモデルとこれらに関係する計算式を組み合わせて使うことができる。統計的分析の形でガラスのモデル化は、新しいデータ、実験手順、測定機関(ガラス研究施設)の評価・認定を支援することができる。
歴史
[編集]歴史的に、ガラス特性の計算はガラス科学の創始と直接関係している。19世紀の末に、物理学者エルンスト・アッベはドイツのイェーナでカール・ツァイスの光学工場との共同作業に刺激され、最適化された光学顕微鏡の設計計算ができる数式を導いた。アッベ以前、顕微鏡は工芸品であり、組み立ては熟練した職人によっていたので、光学顕微鏡は非常に高価であり、品質にもばらつきがあった。アッベはどのように最高の顕微鏡を組み立てればよいかが分かったが、これに必要な特定の屈折率と分散を持つレンズとプリズムは存在していなかった。アッベはガラス工芸家や技術者からは答えを得ることができなかった。この時代のガラス作りは科学に基づいたものではなかった。[2]
1879年、ガラス技術者オットー・ショットは、特別な光学的性質を期待して自分で作成した特殊な配合のガラス試料(ケイ酸リチウムガラス)をアッベに送った。アッベの測定によると、ショットのガラスは期待した特性ではなかった。にもかかわらず、アッベはこの問題をさらに研究し、すべてのガラス成分を系統的に評価するようにショットを招いた。最終的に、ショットは均質なガラスの試料を作ることに成功し、アッベが望んでいた光学特性を持つホウケイ酸ガラスを発明した。[2]これらの発明が有名なカール・ツァイスとショット社を興す基になった(顕微鏡技術の年表を参照)。系統的なガラス研究がここに始まった。1908年、Eugene Sullivan もアメリカでガラスの研究を開始した(コーニング、ニューヨーク州)。[3]
ガラス研究の初期には、ガラスの組成と特性との関係を知ることが最も重要であった。この目的のため、ショットはいくつかの書物でガラス特性の計算に加法則[訳語疑問点]を導入した。[4][5][6]この原理は、ガラスの組成と特定の物性がすべての成分の濃度と線形であることを暗示しており、下の式で Ci と bi がそれぞれ理想的なガラス成分とそれに対応する係数となる理想混合物を仮定している。加法則は単純化であり、屈折率と粘度のグラフに見られるように、狭い組成範囲でのみ有効である。にもかかわらず、光学ガラス、調理や研究に使われる低熱膨張ガラス(Pylex、Duranなど)、水銀温度計用に凝固点降下の小さいガラスなど、ショット社の発明の多くに加法則が使われている。その後、English[7]と Gehlhoff et al.[8]が同様に加法的なガラスの特性計算モデルを発表した。ショットの加法則は今日でもガラスの研究開発に広く使われている。[9][10]
- 加法則:
グローバルモデル
[編集]

その後、ショットと多くの科学者・技術者たちは、十分狭い組成範囲について、自分たちの研究所で測定された実験値を加法則にあてはめた(ローカルガラスモデル)。研究所間の不一致や、非線形なガラス成分の作用を考える必要がないため、これは大変便利だった。数十年にわたる系統的なガラス研究の進行により、何千種類のガラス組成が研究された結果、何百万のガラス特性が発表され、ガラスデータベースに集められた。この膨大な実験データの集積は、Bottinga[13]、 Kucuk[14]、 Priven[15]、 Choudhary[16]、 Mazurin[17]、 Fluegel[18][19]が様々なアプローチによるグローバルガラスモデルを発表するまで全体としての研究がされていなかった。ショットのモデルとは対照的に、グローバルガラスモデルは多くの独立したデータ源を考慮しており、モデルによる推定はより確からしいものになっている。グローバルガラスモデルはさらに、右図に見られる混合アルカリ効果やホウ素特例[訳語疑問点]のように、特定のガラス成分の組み合わせが特性に及ぼす非線形効果を明らかにし定量化した。グローバルガラスモデルはまた、ガラス特性測定の正確度の興味深い発達を反映している。たとえば、図示したように現代の科学文献におけるいくつかのガラス特性の実験データの正確度の低下である。これらは、新しいデータ、測定手順、測定機関(ガラス研究施設)の評価・認定に利用することができる。以下の節では、(融解熱を除いて)膨大な実験データをうまく扱えるように見える経験的なモデル化手法を述べる。得られるモデルは今日の工業的応用やガラスの特性計算の研究に利用されている。
非経験的(演繹的)ガラスモデルも存在する。[20]それらはそもそもガラス特性の確かな予測を得るためでなく、しばしばいくつかの特性(原子半径、原子量、化学結合の強さと結合角、結合の価数、比熱)の間の関係を確立して科学的な洞察を得るために作られたものである。将来的には、諸特性間の関係が十分に理解され、必要なすべての実験データが利用可能であれば、演繹的モデルにおける特性間の関係の研究により、最終的には求める特性すべてについて精度の高い予測が導かれる可能性がある。
手法
[編集]ガラスの特性と製造中の挙動は、GE-SYSTEM[21]、SciGlass[22]、 Interglad[23]のようなガラスデータベースの統計的な分析により、時には有限要素法と結びつけることで、計算することができる。融解熱の見積もりには熱力学データベースを用いる。
線形回帰
[編集]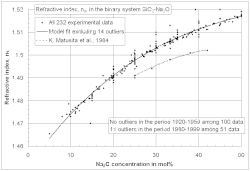
求めたいガラス特性が結晶化や相分離に関係がない場合(たとえば液相線温度)、3次までの一般化多項式[訳語疑問点]を使った線形回帰を利用できる。下は2次式の例である。C は%またはその他の単位によるNa2OやCaOのようなガラス成分の濃度、b は係数、n はガラス成分の数である。すべての成分を合計すると100%になるため変数が過剰になるので、ガラスの主成分であるシリカ(SiO2)は下の式からはずす。下式の多くの項は相関と有意性の分析に基づいて無視することができる。図に見られるような系統誤差はダミー変数によって定量化される。さらなる詳細とその他の例はFluegel[24]のオンライン・チュートリアルで見ることができる。
非線形回帰
[編集]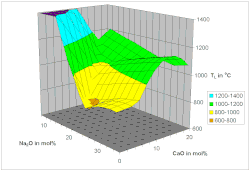
液相線温度はニューラルネットワーク[26]と離散的なピーク関数を用いた非直線回帰によってモデル化されている。[25]離散的なピーク関数のアプローチは、1つの初晶領域の中では線形回帰が適用でき[27]、共晶点で突然に変化が起こるという観測に基づいている。
ガラスの融解熱
[編集]ガラスの融解熱は、原料の混合物(バッチ)を溶融ガラスにするために必要なエネルギーの量を反映する。これは、バッチおよびガラスの組成、炉および廃熱回収システムの効率、ガラスの炉内滞留時間の平均、その他の多くの因子に依存する。Carl Krögerが1953年にこの問題についての先駆的な論文を書いた。[28]
有限要素法
[編集]ガラス溶融炉内のガラスの流れをモデル化するために、溶融ガラスの粘度、密度、熱伝導率、比熱、吸収スペクトル、その他の関連する特性についてのデータまたはモデルに基づいて、有限要素法が商業的に応用されている。[29][30] 有限要素法はまた、ガラスの成形工程にも応用されることがある。
複数の特性の最適化
[編集]生産コストを含め、いくつかのガラス特性を同時に最適化することがしばしば要求される。[21][31] これは次のようにシンプレックス法または表計算ソフトで行うことができる。
- 求める特性の一覧を作成する。
- 信頼性をもって組成に基づいたガラスの特性計算ができるように、モデルを入力する。生産コストを見積もる計算式を含む。
- 望む特性と計算された特性との間の差(誤差)の2乗を計算する。
- ガラス成分を変数として誤差の2乗の合計(残差平方和)を減らす。例えばMicrosoft Excelのソルバーオプション[32] を使用する。最適化に他のソフト(例えばOrigin)を使うこともできる。
望む特性ごとに異なる重みをつけることもできる。原理についての基本的な情報はHuff et al.[33]の論文に見られる。いくつかのガラスモデルの組み合わせに、さらに関連する技術的および財務的関数を加えたものは、シックス・シグマの最適化に使うことができる。
関連項目
[編集]脚注
[編集]- ^ Calculation of the Refractive Index of Glasses
- ^ a b Vogel, Werner (1994). Glass chemistry (2nd revised ed.). Berlin: Springer-Verlag. ISBN 3-540-57572-3
- ^ Eugene Sullivan and Corning Glass Works
- ^ Winkelmann A.; Schott O. (1894). “Über die Elastizität und über die Druckfestigkeit verschiedener neuer Gläser in ihrer Abhängigkeit von der chemischen Zusammensetzung”. Annalen der Physik und Chemie 51: 697.
- ^ Winkelmann A.; Schott O. (1894). “Über thermische Widerstandscoefficienten verschiedener Gläser in ihrer Abhängigkeit von der chemischen Zusammensetzung”. Annalen der Physik und Chemie 51: 730. Bibcode: 1894AnP...287..730W. doi:10.1002/andp.18942870407.
- ^ Winkelmann A.; Schott O. (1893). “Über die specifischen Wärmen verschieden zusammengesetzter Gläser”. Annalen der Physik und Chemie 49: 401. Bibcode: 1893AnP...285..401W. doi:10.1002/andp.18932850702.
- ^ English S. (1924). “The effect of composition on the viscosity of glass. Part II”. J. Soc. Glass Technol. 8: 205–48.
“... Part III Some Four-component Glasses”. J. Soc. Glass Technol. 9: 83–98. (1925).
“...Part IV. Calculation of the Influence of Minor Constituents”. J. Soc. Glass Technol. 10: 52–66. (1926). - ^ Gehlhoff G.; Thomas M. (1925). Z. Tech. Phys. (6): 544.; Z. Tech. Phys. (7): 105, 260. (1926).; "Lehrbuch der technischen Physik", J. A. Barth-Verlag, Leipzig, 1924, p 376.
- ^ Lakatos T.; Johansson L.G.; Simmingsköld B. (June 1972). “Viscosity temperature relations in the glass system SiO2-Al2O3-Na2O-K2O-CaO-MgO in the composition range of technical glasses”. Glass Technology 13 (3): 88–95.
- ^ Terese Vascott; Thomas P. Seward III (2005). High Temperature Glass Melt Property Database for Process Modeling. Wiley-American Ceramic Society. ISBN 1-57498-225-7
- ^ The Mixed-Alkali Effect for the Viscosity of Glasses
- ^ a b Overview, Measurement Errors of Glass Properties
- ^ Bottinga Y.; Weill D.F. (May 1972). “The viscosity of magmatic silicate liquids: a model for calculation”. Am. J. Sci. 272 (5): 438–75. doi:10.2475/ajs.272.5.438.
- ^ Kucuk A.; Clare A. G; Jones L. (October 1999). “An estimation of the surface tension of silicate glass melts at 1400 °C using statistical analysis”. Glass Technol. 40 (5): 149–53.
- ^ Priven A.I. (December 2004). “General Method for Calculating the Properties of Oxide Glasses and Glass-Forming Melts from their Composition and Temperature”. Glass Technology 45 (6): 244–54.
- ^ M. K. Choudhary; R. M. Potter (2005). “9. Heat Transfer in Glass-Forming Melts”. In Angelo Montenero; Pye, David; Innocent Joseph. Properties of Glass-Forming Melts. Boca Raton: CRC. ISBN 1-57444-662-2
- ^ O. V. Mazurin, O. A. Prokhorenko: "Electrical conductivity of glass melts"; Chapter 10 in: "Properties of Glass-Forming Melts" ed. by D. L. Pye, I. Joseph, A. Montenaro; CRC Press, Boca Raton, Florida, 2005, ISBN 1-57444-662-2.
- ^ Fluegel A. (2007). “Glass Viscosity Calculation Based on a Global Statistical Modeling Approach” (PDF). Glass Technol.: Europ. J. Glass Sci. Technol. A 48 (1): 13–30.
- ^ Fluegel, Alexander (2007). “Global Model for Calculating Room-Temperature Glass Density from the Composition”. Journal of the American Ceramic Society 90 (8): 2622. doi:10.1111/j.1551-2916.2007.01751.x.
- ^ Milos B. Volf: "Mathematical Approach to Glass" Glass Science and Technology, vol. 9, Elsevier, 1988, ISBN 0-444-98951-X
- ^ a b GE-SYSTEM
- ^ SciGlass Archived 2007-10-16 at the Wayback Machine.
- ^ Interglad
- ^ A. Fluegel: Statistical Regression Modeling of Glass Properties - A Tutorial
- ^ a b Glass Liquidus Temperature Calculation using disconnected peak functions
- ^ Dreyfus, C (2003). “A machine learning approach to the estimation of the liquidus temperature of glass-forming oxide blends”. Journal of Non-Crystalline Solids 318: 63. Bibcode: 2003JNCS..318...63D. doi:10.1016/S0022-3093(02)01859-8.
- ^ Hanni J.B.; Pressly E.; Crum J.V.; Minister K.B.C.; Tran D.; Hrma P.; Vienna J.D. (2005). “Liquidus temperature measurements for modeling oxide glass systems relevant to nuclear waste vitrification”. Journal of Materials Science 20 (12): 3346–57. Bibcode: 2005JMatR..20.3346H. doi:10.1557/JMR.2005.0424.
- ^ Kröger, Carl (1953). “Theoretischer Wärmebedarf der Glasschmelzprozesse (Theoretical heat demand of glass melting processes)” (German). Glastechnische Berichte 26 (7): 202–14.
- ^ Glass Service, Furnace Design
- ^ Brochure: Flow modeling software for the glass industry, Fluent Inc.
- ^ Glass property optimization
- ^ Excel Solver
- ^ Huff, N. T.; Call, A. D. (1973). “Computerized Prediction of Glass Compositions from Properties”. Journal of the American Ceramic Society 56 (2): 55. doi:10.1111/j.1151-2916.1973.tb12356.x.


