三角関数 (さんかくかんすう、英 : trigonometric function )とは、平面三角法 における、角 の大きさと線分 の長さの関係を明らかにする関数 の族および、それらを拡張して得られる関数の総称である。
∠C を直角とする直角三角形ABC 直角三角形 において、1つの鋭角の大きさが決まれば、三角形 の内角の和は180°であることから他の1つの鋭角の大きさも決まり、3辺の比も決まる。ゆえに、角度に対して辺比の値を与える関数を考えることができる。
∠C を直角とする直角三角形ABC において、AB = h , BC = a , CA = b とおく。∠A = θ に対して h : a : b が決まることから、
sin
θ
=
a
h
{\displaystyle \sin \theta ={\frac {a}{h}}}
cos
θ
=
b
h
{\displaystyle \cos \theta ={\frac {b}{h}}}
tan
θ
=
a
b
=
sin
θ
cos
θ
{\displaystyle \tan \theta ={\frac {a}{b}}={\frac {\sin \theta }{\cos \theta }}}
cosec
θ
=
h
a
=
1
sin
θ
{\displaystyle {\text{cosec}}\,\theta ={\frac {h}{a}}={\frac {1}{\sin \theta }}}
sec
θ
=
h
b
=
1
cos
θ
{\displaystyle \sec \theta ={\frac {h}{b}}={\frac {1}{\cos \theta }}}
cot
θ
=
b
a
=
1
tan
θ
{\displaystyle \cot \theta ={\frac {b}{a}}={\frac {1}{\tan \theta }}}
という6つの値が定まる。それぞれ正弦 (sine(サイン))・余弦 (cosine(コサイン))・正接 (tangent(タンジェント))・余割 (cosecant(コセカント))・正割 (secant(セカント))・余接 (cotangent(コタンジェント))と呼び、まとめて三角比 と呼ばれる。ただし cosec は長いので csc と略記することも多い。また、余弦、余割、余接は余角(角を90°から引いた角)のそれぞれ正弦、正割、正接に等しい。三角比は平面三角法 に用いられ、巨大な物の大きさや遠方までの距離を計算する際の便利な道具となる。角度 θ の単位は、通常度 またはラジアン である。
単位円による、6つの三角関数が表す長さ 実数 t に対して、2次元ユークリッド空間 R 2 における単位円 x 2 + y 2 = 1 上の点P(x , y ) を ∠x OP = t (反時計回りを正の向きとする)を満たすように取り、
sin
t
=
y
{\displaystyle \sin t=y}
cos
t
=
x
{\displaystyle \cos t=x}
tan
t
=
y
x
=
sin
t
cos
t
{\displaystyle \tan t={\frac {y}{x}}={\frac {\sin t}{\cos t}}}
と定義する。順に正弦関数 (sine; サイン)・余弦関数 (cosine; コサイン)・正接関数 (tangent; タンジェント)と呼び、これらを総称して三角関数 と呼ぶ。さらにこれらの逆数
csc
t
=
1
y
=
1
sin
t
{\displaystyle \csc t={\frac {1}{y}}={\frac {1}{\sin t}}}
sec
t
=
1
x
=
1
cos
t
{\displaystyle \sec t={\frac {1}{x}}={\frac {1}{\cos t}}}
cot
t
=
x
y
=
1
tan
t
{\displaystyle \cot t={\frac {x}{y}}={\frac {1}{\tan t}}}
を順に余割関数 (cosecant; コセカント)・正割関数 (secant; セカント)・余接関数 (cotangent; コタンジェント)と呼び、これらを総称して割三角関数 (かつさんかくかんすう)と呼ぶ。これらを含めて三角関数と呼ぶこともある。
角度、辺の長さといった幾何学的な概念に依存しないために、級数 で定義することもできる。収束半径を求めることより、以下の級数は収束円上で収束する。
z を複素数、Bn をベルヌーイ数 、En をオイラー数 とする。
sin
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
!
z
2
n
+
1
for all
z
{\displaystyle \sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}\quad {\text{for all}}\ z}
cos
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
z
2
n
for all
z
{\displaystyle \cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}\quad {\text{for all}}\ z}
tan
z
=
∑
n
=
1
∞
(
−
1
)
n
2
2
n
(
1
−
2
2
n
)
B
2
n
(
2
n
)
!
z
2
n
−
1
for
|
z
|
<
π
2
{\displaystyle \tan z=\sum _{n=1}^{\infty }{\frac {(-1)^{n}2^{2n}(1-2^{2n})B_{2n}}{(2n)!}}z^{2n-1}\quad {\text{for}}\ |z|<{\frac {\pi }{2}}}
csc
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
−
2
2
n
)
B
2
n
(
2
n
)
!
z
2
n
−
1
for
0
<
|
z
|
<
π
{\displaystyle \csc z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2-2^{2n})B_{2n}}{(2n)!}}z^{2n-1}\quad {\text{for}}\ 0<|z|<\pi }
sec
z
=
∑
n
=
0
∞
(
−
1
)
n
E
2
n
(
2
n
)
!
z
2
n
for
|
z
|
<
π
2
{\displaystyle \sec z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}z^{2n}\quad {\text{for}}\ |z|<{\frac {\pi }{2}}}
cot
z
=
∑
n
=
0
∞
(
−
1
)
n
2
2
n
B
2
n
(
2
n
)
!
z
2
n
−
1
for
0
<
|
z
|
<
π
{\displaystyle \cot z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}}{(2n)!}}z^{2n-1}\quad {\text{for}}\ 0<|z|<\pi }
一定の半径の円における中心角に対する弦 と弧 の長さの関係は、測量 や天文学 の要請によって古代から研究されてきた。
古代ギリシャにおいて、円と球に基づく宇宙観に則った天文学研究から、ヒッパルコス により一定の半径の円における中心角に対する弦の長さが表にまとめられたもの(正弦表)が作られた。プトレマイオス の『アルマゲスト 』にも正弦表が記載されている。
正弦表は後にインドに伝わり、弦の長さは半分でよいという考えから5世紀 頃には半弦 ardha-jiva(つまり現在の sine の意味の正弦)の長さをより精確にまとめたものが作成された(『アールヤバタ』)。ardha は"半分" jiva は"弦"の意味で、当時のインドではこの半弦(現在の sine の意味の正弦)は単に jiva と略された。また、弦の長さを半分にして直角三角形を当てはめたことから派生して余角 (complementary angle) の考えが生まれ、“余角 (co-angle) の正弦 (sine)”という考えから余弦 (cosine) の考えが生まれた。余弦の値もこの頃に詳しく調べられている。(*co- は complementary の略で、補完的・補足的という意味の接頭語として用いる)
8世紀 頃イスラム帝国へ伝わったときに jaib(入り江)と変化した。10世紀のアッバース朝 時代にシリアの数学者アル・バッターニ が正弦法の導入、コタンジェント表の計算、球面三角法(球面幾何学 )の定理を提唱した。ブワイフ朝 のバグダード の数学者アブル・ワファー がタンジェント を導入した(al-Marwazi 説もある)。
一説では12世紀にチェスターのロバート がラテン語 に翻訳した際、正弦を sinus rectus と意訳し(sinusはラテン語で「湾」のこと)、現在の sine になったという。円や弦といった概念からは独立に、三角比を辺の比として角と長さの関係と捉えたのは16世紀 オーストリアのゲオルク・レティクス であるといわれる。余弦を co-sine と呼んだり、sin, cos という記号が使われるようになったりしたのは 17世紀 になってからであり、それが定着するのは 18世紀 オイラー の頃である。一般角に対する三角関数を定義したのはオイラーである。
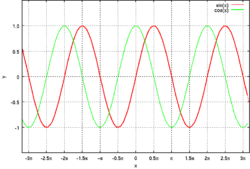
sin x と cos x のグラフ。周期性が確認できる x 軸の正の部分となす角は
t
=
θ
+
2
π
n
(
0
≤
θ
<
2
π
,
n
∈
Z
)
{\displaystyle t=\theta +2\pi n\ (0\leq \theta <2\pi ,n\in \mathbb {Z} )}
と表すことができ、θ を偏角 、t を一般角 と言う。
一般角 t が 2π 進めば点 P(cos t , sin t ) は単位円上を1周し元の位置に戻る。従って、
cos
(
t
+
2
π
n
)
=
cos
t
{\displaystyle \cos(t+2\pi n)=\cos t}
sin
(
t
+
2
π
n
)
=
sin
t
{\displaystyle \sin(t+2\pi n)=\sin t}
すなわち cos, sin は周期 2π の周期関数 である。
ほぼ同様に、tan, cot は周期 π の周期関数、sec, csc は周期 2π の周期関数である。
三角関数のグラフ: Sine , Cosine , Tangent , Cosecant(点線) , Secant(点線) , Cotangent(点線)
単位円上の点の座標の関数であることから、三角関数の間には多数の相互関係が存在する。
基本相互関係
全てピタゴラスの定理 により証明される。
sin2 θ + cos2 θ = 1
sec
2
θ
−
tan
2
θ
=
1
cos
2
θ
−
tan
2
θ
=
1
{\displaystyle \sec ^{2}\theta -\tan ^{2}\theta ={\frac {1}{\cos ^{2}\theta }}-\tan ^{2}\theta =1}
csc
2
θ
−
cot
2
θ
=
1
sin
2
θ
−
1
tan
2
θ
=
1
{\displaystyle \csc ^{2}\theta -\cot ^{2}\theta ={\frac {1}{\sin ^{2}\theta }}-{\frac {1}{\tan ^{2}\theta }}=1}
負角・余角・補角公式
sin(−θ ) = −sin θ
cos(−θ ) = cos θ
tan(−θ ) = −tan θ
sin
(
π
2
−
θ
)
=
cos
θ
{\displaystyle \sin \left({\frac {\pi }{2}}-\theta \right)=\cos \theta }
cos
(
π
2
−
θ
)
=
sin
θ
{\displaystyle \cos \left({\frac {\pi }{2}}-\theta \right)=\sin \theta }
tan
(
π
2
−
θ
)
=
cot
θ
=
1
tan
θ
{\displaystyle \tan \left({\frac {\pi }{2}}-\theta \right)=\cot \theta ={\frac {1}{\tan \theta }}}
sin(π − θ ) = sin θ
cos(π − θ ) = −cos θ
tan(π − θ ) = −tan θ π 回転・π / 2
sin(θ + π ) = −sin θ
cos(θ + π ) = −cos θ
tan(θ + π ) = tan θ
sin
(
θ
+
π
2
)
=
cos
θ
{\displaystyle \sin \left(\theta +{\frac {\pi }{2}}\right)=\cos \theta }
cos
(
θ
+
π
2
)
=
−
sin
θ
{\displaystyle \cos \left(\theta +{\frac {\pi }{2}}\right)=-\sin \theta }
tan
(
θ
+
π
2
)
=
−
cot
θ
=
−
1
tan
θ
{\displaystyle \tan \left(\theta +{\frac {\pi }{2}}\right)=-\cot \theta =-{\frac {1}{\tan \theta }}}
sin(α + β ) = sin α cos β + cos α sin β
sin(α − β ) = sin α cos β − cos α sin β
cos(α + β ) = cos α cos β − sin α sin β
cos(α − β ) = cos α cos β + sin α sin β
tan
(
α
+
β
)
=
tan
α
+
tan
β
1
−
tan
α
tan
β
{\displaystyle \tan(\alpha +\beta )={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}}
tan
(
α
−
β
)
=
tan
α
−
tan
β
1
+
tan
α
tan
β
{\displaystyle \tan(\alpha -\beta )={\frac {\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }}}
1. 加法定理は、オイラーの公式 から簡単に導出できる。
cos(α + β ) + i sin(α + β ) = e (α +β )i (オイラーの公式)
= eαi eβi
= (cos α + i sin α )(cos β + i sin β )
= (cos α cos β − sin α sin β ) + i (sin α cos β + cos α sin β ) 両辺の実部、虚部を比較すると、それぞれ sin, cos の加法公式を得る。また、
tan
(
α
±
β
)
=
sin
α
cos
β
±
cos
α
sin
β
cos
α
cos
β
∓
sin
α
sin
β
{\displaystyle \tan \left(\alpha \pm \beta \right)={\frac {\sin \alpha \cos \beta \pm \cos \alpha \sin \beta }{\cos \alpha \cos \beta \mp \sin \alpha \sin \beta }}}
において分母と分子を cos α cos β で割ると tan の加法公式が得られる。
この導出法は、オイラーの公式を既知とするように三角関数の導入(たとえば三角関数をべき級数 として定義)していなければ証明として通用しない。
2. また、単位円上の2点間の距離を求める方法でも求められる。
PQ2 は、2通りの方法で求められる。 単位円周上に2点 P(cos α , sin α ), Q(cos β , sin β ) を取り、P と Q の距離の2乗 PQ2 を2通りの方法で求めることを考える。(右図も参照)
(1) 三平方の定理より求める
PQ2 = (cos α − cos β )2 + (sin α − sin β )2
= 2 − 2cos α cos β − 2sin α sinβ
(2) 余弦定理より求める
PQ2 = 12 + 12 − 2・1・1・cos(α − β )
= 2 − 2cos(α − β ) (1), (2) より、PQ2 を媒介すると、
2 − 2cos α cos β − 2sin α sin β = 2 − 2cos(α − β )
∴ cos(α − β ) = cos α cos β + sin α sin β これより、他の3つの公式は次々に求まる。
cos(α + β ) = cos α cos β − sin α sin β 元の等式の α に
π
2
−
α
{\displaystyle {\frac {\pi }{2}}-\alpha }
sin(α + β ) = sin α cos β + cos α sin β sin(α − β ) = sin α cos β − cos α sin β (導出および証明終)
三角関数の微積分は、以下の表の通りである。
f
(
x
)
{\displaystyle f(x)}
f
′
(
x
)
{\displaystyle f'(x)}
∫
f
(
x
)
d
x
{\displaystyle \int f(x)\,dx}
sin
x
{\displaystyle \sin x}
cos
x
{\displaystyle \cos x}
−
cos
x
+
C
{\displaystyle -\cos x+C}
cos
x
{\displaystyle \cos x}
−
sin
x
{\displaystyle -\sin x}
sin
x
+
C
{\displaystyle \sin x+C}
tan
x
{\displaystyle \tan x}
sec
2
x
=
1
+
tan
2
x
{\displaystyle \sec ^{2}x=1+\tan ^{2}x}
−
ln
|
cos
x
|
+
C
{\displaystyle -\ln \left|\cos x\right|+C}
cot
x
{\displaystyle \cot x}
−
csc
2
x
=
−
(
1
+
cot
2
x
)
{\displaystyle -\csc ^{2}x=-(1+\cot ^{2}x)}
ln
|
sin
x
|
+
C
{\displaystyle \ln \left|\sin x\right|+C}
sec
x
{\displaystyle \sec x}
sec
x
tan
x
{\displaystyle \sec x\tan x}
ln
|
sec
x
+
tan
x
|
+
C
{\displaystyle \ln \left|\sec x+\tan x\right|+C}
csc
x
{\displaystyle \csc x}
−
csc
x
cot
x
{\displaystyle -\csc x\cot x}
−
ln
|
csc
x
+
cot
x
|
+
C
{\displaystyle -\ln \left|\csc x+\cot x\right|+C}
三角関数の微分では、次の極限
lim
h
→
0
sin
h
h
=
1
{\displaystyle \lim _{h\to 0}{\frac {\sin h}{h}}=1}
の成立が基本的である。このとき、sin x の導関数 が cos x であることは加法定理から従う。さらに余角公式 cos x = sin(π / 2 x ) から cos x の導関数は −sin x である。即ち、sin x は微分方程式
d
2
y
d
x
2
+
y
=
0
{\displaystyle {\frac {d^{2}y}{dx^{2}}}+y=0}
特殊解 である。また、他の三角関数の導関数も、上の事実から簡単に導ける。
三角関数は以下のようにテイラー級数 に展開される。解析学 では、幾何的な性質へ言及せず、これらの表示を三角関数の定義 とすることがある。z は任意の複素数、Bn はベルヌーイ数 、En は オイラー数 である。
sin
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
!
z
2
n
+
1
for all
z
{\displaystyle \sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}\quad {\mbox{ for all }}z}
cos
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
z
2
n
for all
z
{\displaystyle \cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}\quad {\mbox{ for all }}z}
tan
z
=
∑
n
=
1
∞
(
−
1
)
n
2
2
n
(
1
−
2
2
n
)
B
2
n
(
2
n
)
!
z
2
n
−
1
for
|
z
|
<
π
2
{\displaystyle \tan z=\sum _{n=1}^{\infty }{\frac {(-1)^{n}2^{2n}(1-2^{2n})B_{2n}}{(2n)!}}z^{2n-1}\quad {\mbox{ for }}|z|<{\frac {\pi }{2}}}
csc
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
−
2
2
n
)
B
2
n
(
2
n
)
!
z
2
n
−
1
for
0
<
|
z
|
<
π
{\displaystyle \csc z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2-2^{2n})B_{2n}}{(2n)!}}z^{2n-1}\quad {\mbox{ for }}0<|z|<\pi }
sec
z
=
∑
n
=
0
∞
(
−
1
)
n
E
2
n
(
2
n
)
!
z
2
n
for
|
z
|
<
π
2
{\displaystyle \sec z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}z^{2n}\quad {\mbox{ for }}|z|<{\frac {\pi }{2}}}
cot
z
=
∑
n
=
0
∞
(
−
1
)
n
2
2
n
B
2
n
(
2
n
)
!
z
2
n
−
1
for
0
<
|
z
|
<
π
{\displaystyle \cot z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}}{(2n)!}}z^{2n-1}\quad {\mbox{ for }}0<|z|<\pi }
三角関数は以下のように無限乗積 に展開される。(→証明 )
sin
π
z
=
π
z
∏
n
=
1
∞
(
1
−
z
2
n
2
)
{\displaystyle \sin \pi z=\pi z\prod _{n=1}^{\infty }{\left(1-{\frac {z^{2}}{n^{2}}}\right)}}
cos
π
z
=
∏
n
=
1
∞
{
1
−
z
2
(
n
−
1
2
)
2
}
{\displaystyle \cos \pi z=\prod _{n=1}^{\infty }\left\{1-{\frac {z^{2}}{(n-{\frac {1}{2}})^{2}}}\right\}}
三角関数は以下のように部分分数 に展開される。(→証明 )
三角関数の定義域を適当に制限したものの逆関数 を逆三角関数 (ぎゃくさんかくかんすう、inverse trigonometric function )と呼ぶ。逆三角関数は逆関数の記法に則り、元の関数の記号に −1 を右肩に付して表す。たとえば逆 正弦関数(ぎゃくせいげんかんすう、inverse sine ; インバース・サイン)は sin−1 x などと表す。arcsin, arccos などの記法もよく用いられる。
x
=
sin
y
⟺
y
=
sin
−
1
x
{\displaystyle x=\sin y\iff y=\sin ^{-1}x}
x
=
cos
y
⟺
y
=
cos
−
1
x
{\displaystyle x=\cos y\iff y=\cos ^{-1}x}
x
=
tan
y
⟺
y
=
tan
−
1
x
{\displaystyle x=\tan y\iff y=\tan ^{-1}x}
x
=
cot
y
⟺
y
=
cot
−
1
x
{\displaystyle x=\cot y\iff y=\cot ^{-1}x}
x
=
sec
y
⟺
y
=
sec
−
1
x
{\displaystyle x=\sec y\iff y=\sec ^{-1}x}
x
=
cosec
y
⟺
y
=
cosec
−
1
x
{\displaystyle x={\text{cosec}}\,y\iff y={\text{cosec}}^{-1}\,x}
である。逆関数は逆数ではないので注意したい。逆数との混乱を避けるために、逆正弦関数 sin−1 x を arcsin x と書く流儀もある。一般に周期関数の逆関数は多価関数 になるので、通常は逆三角関数を一価連続 なる枝 に制限して考えることが多い。たとえば、便宜的に主値
−
π
2
≤
sin
−
1
x
≤
π
2
{\displaystyle -{\frac {\pi }{2}}\leq \sin ^{-1}x\leq {\frac {\pi }{2}}}
0
≤
cos
−
1
x
≤
π
{\displaystyle 0\leq \cos ^{-1}x\leq \pi }
−
π
2
<
tan
−
1
x
<
π
2
{\displaystyle -{\frac {\pi }{2}}<\tan ^{-1}x<{\frac {\pi }{2}}}
のように選ぶことが多い。またこのとき、制限があることを強調するために、Sin−1 x , Arcsin x のように頭文字を大文字にした表記がよく用いられる。
三角関数の微分に関する性質から、cos x , sin x をテイラー展開 することにより、かの有名なオイラーの公式 exp ix = cos x + i sin x が導かれる。これより、2つの等式、
exp ix = cos x + i sin x ix ) = cos x − i sin x
が得られるから、これを連立させて解くことにより、正弦関数・余弦関数の初等関数 としての表現が可能となる。即ち、
cos
x
=
e
i
x
+
e
−
i
x
2
,
{\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}},}
sin
x
=
e
i
x
−
e
−
i
x
2
i
.
{\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}.}
この事実を用いて、三角関数の定義域を複素数全体に拡張することができる。まず、
cos
i
x
=
e
−
x
+
e
x
2
=
cosh
x
,
{\displaystyle \cos ix={\frac {e^{-x}+e^{x}}{2}}=\cosh x,}
sin
i
x
=
e
−
x
−
e
x
2
i
=
i
sinh
x
{\displaystyle \sin ix={\frac {e^{-x}-e^{x}}{2i}}=i\sinh x}
である。ここで cosh x , sinh x は双曲線関数 を指す。この等式は三角関数と双曲線関数の関係式と捉えることもできる。任意の複素数 z は z = x + iy (x , y ∈ R ) と表現できるから、加法定理より
cos z = cos(x + iy ) = cos x cosh y − i sin x sinh y ,
sin z = sin(x + iy ) = sin x cosh y + i cos x sinh y が成り立つ。これこそが正弦関数・余弦関数の定義域を複素数全体に拡張したものである。他の三角関数も正弦関数と余弦関数の四則演算によって定義できるから、結局全ての三角関数は定義域を複素数全体に拡張できることが分かる。
cos(x + iy ) の実部のグラフ
cos(x + iy ) の虚部のグラフ
sin(x + iy ) の実部のグラフ
sin(x + iy ) の虚部のグラフ
球面の三角形ABC の内角を a , b , c , 各頂点の対辺に関する球の中心角を α , β , γ とするとき、次のような関係が成立する。余弦公式や正弦余弦公式は式の対称性により各記号を入れ替えたものも成立する。
正弦公式: sin a : sin b : sin c = sin α : sin β : sin γ
余弦公式: cos a = −cos b cos c + sin b sin c cos α
余弦公式: cos α = cos β cos γ + sin β sin γ cos a
正弦余弦公式: sin a cos β = cos b sin c − sin b cos c cos α
Template:Link FA
Template:Link GA
Template:Link FA
Template:Link GA