比較静学
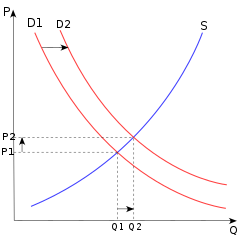
経済学において、比較静学(英: comparative statics)とは、ある経済の外生的パラメータを変化させ、その経済の外生的パラメータの変化前と変化後の二つの異なる結果を比較するものである[1]。
静学の研究では、(もし調整過程が存在するのなら)調整過程後の、二つの異なる均衡状態を比較する。静学においては均衡へ向かう「動き(motion)」や変化そのものの過程は考慮されない。
基本的には比較静学はある一つの市場における需要と供給の変化の研究や、金融政策や財政政策の変化がマクロ経済全体に及ぼす影響を調べる研究に使われている。「比較静学」という言葉そのものは、通常、マクロ経済学よりもミクロ経済学(一般均衡分析を含む)との関連で使用される。比較静学という言葉はジョン・ヒックス(1939)とポール・サミュエルソン(1947) (Kehoe, 1987, p. 517)によって形式化されたが、比較静学という概念は少なくとも1870年代には図を用いた形で提示されていた[2]。新古典派の成長モデル(en:neoclassical growth model)のような静的均衡モデルに対して、比較動学は比較静学に相対するものである(Eatwell, 1987)。
線形近似
[編集]比較静学による結果は、通常、en:implicit function theoremを用いて、均衡が静的であるとの仮定の下、均衡を定義する等式系の線形近似を計算することで導出される。これはすなわち、もし十分に小さな外生的パラメータの変化を考えるならば、それぞれの外生変数がどのように変化するのかを均衡の等式に出現する項の微分のみを用いて計算することができる。
例えば、ある外生変数の均衡値が次の等式で決定されるとする。
ここでは外生パラメータ。そして、一次近似に際して、の小さな変化に起因するの変化は次の条件を満たさなくてはいけない。
ここではの変化を表し、の変化はの変化を表している。また、とは、の、それぞれとに関する偏導関数(ただし、との初期値で計算されたもの)。これと等価的に、 の変化を次のように書くことができる。
この等式をdaで 割ることで x の a に関するComparative static derivativeを得る。これは a の x に関する乗数とも呼ばれる。
複数の等式と複数の未知数
[編集]上記のすべての等式は個の未知数の個の等式の系である場合、真であり続ける。言い換えれば、は「個の未知数のベクトル」および「個の所与のパラメータのベクトル」を含む個の等式の系を示すということである。
もしパラメータが十分に小さな変化をするのであれば、その結果としての内生変数の変化をとして任意によく近似することができる。 このとき、 は変数に関する関数の×の偏導関数の行列を表しており、は関数のパラメータに関する×の偏導関数の行列を表している(との導関数はとの初期値で計算されたもの)。
ひとつの外生変数のひとつの内生変数に対する比較静学的な効果だけを求めるのであれば、全微分された等式系に対してクラメルの公式が使用可能な点に注意。
脚注
[編集]- ^ (Mas-Colell, Whinston, and Green, 1995, p. 24; Silberberg and Suen, 2000)
- ^ Fleeming Jenkin (1870), "The Graphical Representation of the Laws of Supply and Demand, and their Application to Labour," in Alexander Grant, Recess Studies and (1872), "On the principles which regulate the incidence of taxes," Proceedings of Royal Society of Edinburgh 1871-2, pp. 618-30., also in Papers, Literary, Scientific, &c, v. 2 (1887), ed. S.C. Colvin and J.A. Ewing via scroll to chapter links.
参考文献
[編集]- John Eatwell et al., ed. (1987). "Comparative dynamics," The en:New Palgrave: A Dictionary of Economics, v. 1, p. 517.
- John R. Hicks (1939). en:Value and Capital.
- Timothy J. Kehoe, 1987. "Comparative statics," The New Palgrave: A Dictionary of Economics, v. 1, pp. 517–20.
- en:Andreu Mas-Colell, Michael D. Whinston, and Jerry R. Green, 1995. Microeconomic Theory.
- Paul A. Samuelson (1947). en:Foundations of Economic Analysis.
- Eugene Silberberg and Wing Suen, 2000. The Structure of Economics: A Mathematical Analysis, 3rd edition.
















