横断性 (数学)
数学において、横断性(おうだんせい,英: transversality[注釈 1])は、空間がどのように交わるかを記述する概念である。横断性は接することの「対極」と見ることができ、一般の位置で役割を果たす。横断性は微分位相幾何学における一般の交わりの概念を定式化する。横断性は交点で交わっている空間の線型化を考えることで定義される。
定義
[編集]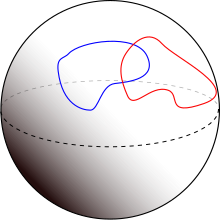

与えられた有限次元の滑らかな多様体の2つの部分多様体が横断的に交わる (intersect transversally) とは,交わっている任意の点において,その点での部分多様体の2つの接空間が多様体の接空間を生成することをいう[2].交わらない多様体たちは自明に横断的に交わる.多様体の次元が相補的ならば(すなわち次元の和が周囲の空間の次元ならば),条件は周囲の多様体の接空間が2つの小さい接空間の直和であることを意味する.交わりが横断的ならば,交わりは余次元が2つの多様体の余次元の和に等しい部分多様体になる.横断性条件が無ければ,交わりはある種の特異点を持つかもしれず部分多様体になるとは限らない.
特にこれは,次元が相補的な横断的に交わる部分多様体が孤立点(すなわち0次元多様体)で交わることを意味する.部分多様体と周囲の多様体がともに向き付けられているとき,交わりも向き付けられている.交わりが 0 次元であるとき,向き付けは単に各点に対して正か負である.
与えられた多様体 M の2つの部分多様体 L1 と L2 の横断的交叉を表す1つの表記は
である.この表記は2通りに読める:「L1 と L2 が横断的に交わる」というのと, L1 と L2 の集合論的交叉 L1 ∩ L2 で交わりが横断的であるときの表記である.この表記で,横断性の定義は:
写像の横断性
[編集]部分多様体の対の横断性の概念は,部分多様体と周囲の多様体への写像の横断性,あるいは周期の多様体への写像の対に,像の交わりの点の原像に沿った接空間の押し出しが周囲の多様体の接空間全体を生成するかどうかを問うことによって,容易に拡張できる[3].写像が埋め込みならば,これは部分多様体の横断性に同値である.
異なる次元に対する横断性の意味
[編集]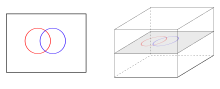
L1, L2, M をそれぞれ次元が l1, l2, m の多様体とし,横断的に交わる写像 f1: L1 → M, f2: L2 → M があるとする.
横断性の意味は M, L1, L2 の相対的な次元に大きく依存して異なる.l1 + l2 = m のときに横断性と接性の関係は最も明白である.
3つの別々の場合を考えることができる:
- l1 + l2 < m のとき,L1 と L2 の接空間の像が M の接空間をはることはどんな点でも不可能である.したがって f1 と f2 のどんな交わりも横断的になり得ない.しかしながら,交わらない多様体は自明な意味で条件を満たすので,横断的に交わると言える.
- l1 + l2 = m のとき,L1 と L2 の接空間の像は任意の交点において M の接空間を直和に張らなければならない.したがってそれらの交わりは孤立した符号付き点からなる,すなわち 0 次元多様体である.
- l1 + l2 > m のとき,L1 と L2 の接空間の和は直和とは限らない.実際,f1 と f2 が,埋め込まれた部分多様体の場合に起こるように,交点ではめ込みであるときには,直和にはなりえない.写像がはめ込みならば,像の交わりは次元 l1 + l2 − m の多様体になる.
交叉積
[編集]任意の2つの滑らかな部分多様体が与えられると,それらの一方を任意に小さい量だけ摂動して,得られる部分多様体が固定された部分多様体と横断的に交わるようにできる.そのような摂動は多様体あるいはそれらの交わりのホモロジー類に影響しない.例えば,次元が相補的な多様体が横断的に交わるとき,交点の個数の符号付き和は,べつの横断交叉な多様体に全同位変形さえしても変わらない.(交点を mod 2 で数えて符号を無視し,粗い不変量を得ることもできる.)これから任意の次元のホモロジー類上の双線型交叉積が定まり,これはコホモロジー上のカップ積にポワンカレ双対である.カップ積と同様,交叉積は次数付き可換である.
横断交叉の例
[編集]横断性の最も簡単な非自明な例は曲面の弧によるものである.2つの弧の交点が横断的であることと接点でないこと,すなわち曲面の接平面内のそれらの接線が相異なることと同値である.
3次元空間では,横断的に交わる曲線は交わらない.局面に横断的に交わる曲線は点で交わり,横断的に交わる2曲面は曲線で交わる.曲面に点で接する曲線(例えば曲面上に乗っている曲線)は曲面と横断的に交わらない.
より専門的な例を挙げよう.G を単純リー群とし, をそのリー環とする.ジャコブソン・モロゾフの定理により,任意の冪零元 はある -triple (e, h, f) に含めることができる. の表現論により,
である.空間 は随伴軌道 Ad(G)e への e での接空間であり,したがってアファイン空間 は e の軌道と横断的に交わる.空間 は Peter Slodowy に因んで スロードウィーの横断片 ("Slodowy slice") と呼ばれる.
応用
[編集]最適制御
[編集]応用として、変分法または関連するポントリャーギンの最大値原理において、横断性条件は最適化問題において求められる解の種類を制御するために頻繁に用いられる。例えば、以下のような問題の解曲線に対して横断性は必要である:
- 問題
- 曲線の一方または両方の端点を固定しないとき、∫F(x, y, y′)dx を最小化せよ。
このような問題の多くにおいてその解は、解曲線がヌルクラインを横断的に横切るという条件を満足する、さもなくば適当なほかの曲線が終点条件を記述する。
解空間の滑らかさ
[編集](写像の横断性の特別の場合を仮定する)サードの定理を用いて、空間の部分多様体で相補的な次元を持つものの間の、あるいは部分多様体および空間への射の間の横断交叉の全体は、それ自身滑らかな部分多様体となることが示せる。
例えば、向き付けられた多様体の接束の滑らかな切断(すなわちベクトル場)を底空間から全空間への射と見たものと零切断(を射または部分多様体と見たもの)は横断的に交わるから、この切断の零点集合(つまりこのベクトル場の特異点集合)は底空間の滑らかな零次元部分多様体(つまり符号付き点集合)を成す。その符号はベクトル場の指数に一致し、従って符号和(つまり零点集合の基本類)は多様体のオイラー標数に等しい。より一般に、向き付けられた滑らかな有限次元閉多様体上のベクトル束に対して、零切断を横断する切断のゼロ点集合は、そのベクトル束の階数に等しい余次元を持つ底空間の部分多様体になり、そのホモロジー類はもとのベクトル束のオイラー類にポワンカレ双対である。
以下はその極めて特別の場合である: 実変数実数値の可微分函数がその零点において零でない微分係数を持つならば、その零点は単純である(すなわち、函数のグラフはその零点において x-軸を横断する)。微分係数が零であることは曲線に水平に接することを意味するのだから、そのような場合には接空間は x-軸に一致することになる。
無限次元の例として以下を挙げる: ∂-作用素はリーマン面から概複素多様体への射の空間上で定義される、ある種のバナッハ空間束の切断で、この切断の零点集合は正則射からなる。この∂-作用素が零切断を横断することが示せるならば、そのモジュライ空間は滑らかな多様体を成す。これらの考察は、擬正則曲線論およびグロモフ–ウィッテン理論において基本的な役割を果たす。(この例における横断性は、バナッハ空間を対象にするために、定義を精緻化する必要があることに注意。)
関連項目
[編集]注
[編集]注釈
[編集]出典
[編集]- ^ Hirsch 1976, p. 66—`"Transversal" is a noun; the adjective is "transverse." —J.H.C. Whitehead, 1959’
- ^ Guillemin & Pollack 1974, p. 30.
- ^ Guillemin & Pollack 1974, p. 28.
参考文献
[編集]- Thom, René (1954). “Quelques propriétés globales des variétés differentiables”. Comm. Math. Helv. 28 (1): 17–86. doi:10.1007/BF02566923.
- Guillemin, Victor; Pollack, Alan (1974). Differential Topology. Prentice-Hall. ISBN 0-13-212605-2
- Hirsch, Morris (1976). Differential Topology. Springer-Verlag. ISBN 0-387-90148-5






![{\displaystyle {\mathfrak {g}}=[{\mathfrak {g}},e]\oplus {\mathfrak {g}}_{f}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca3d22d9eb3814acfe1ee8f250b1537642974845)
![{\displaystyle [{\mathfrak {g}},e]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46f0f2646cff543757ce17c8a942253034595694)
