標準得点

標準得点（ひょうじゅんとくてん、standard score）とは、期待値や標準偏差などの集団基準を用いて、母集団の中における個人の相対的な位置づけが分かるように変換した得点のこと。標準得点に変換することを標準化と呼ぶ^[1]。

Z得点

Z得点（z値、z-score、z-value）とは、平均が0、標準偏差 (SD) が1になるように変換した得点である。もとの母集団が正規分布に従っているとき、Z得点は、必ず標準正規分布に従う。

母集団の平均と標準偏差が既知の場合、確率変数 $x$ のZ得点 $z$ は以下のように計算される^[2]。

z={\frac {x-\mu }{\sigma }}

ここで、 $μ$ は母集団の平均、 $σ$ は母集団の標準偏差を表す。

→詳細は「偏差値」を参照

偏差値とは、平均が50、標準偏差 (SD) が10となるように変換した得点である。T得点（T値、T-score）も同義である。教育分野でしばしば用いられる。

偏差IQとは、正規分布上で平均が100、標準偏差 (SD) が15（ウェクスラー式の場合）または16（ビネー式の場合）となるように変換した得点である。

※以下、偏差IQは、SDが15の場合について説明している。

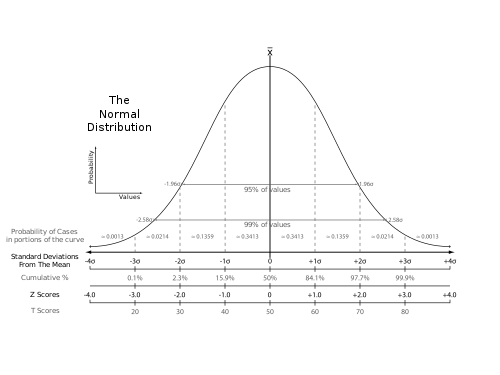
標準正規分布, 偏差値, 偏差IQの関係をグラフ上に表すと、次のようになる。

→詳細は「分位数」を参照

標準正規分布の面積は右図の通り。

平均、標準偏差を変換してもその比率は変わらないので、正規分布上で特定の得点間に含まれる割合は決まっている。

例えば偏差IQは、全体の約68.26%の人が85～115の得点をとり、約95.44%の人が70～130の得点をとる。

この割合をもとに、得点の低い所から順位をつけたものをパーセンタイル順位（下図は偏差IQの場合）という。

例えば、IQ85とは、母集団の下から16パーセンタイルの順位にいることを意味する。