方法 (アルキメデスの著書)
『方法』(ギリシア語: Περὶ μηχανικῶν θεωρημάτων πρὸς Ἐρατοσθένη ἔφοδος, 英語: The Method of Mechanical Theorems)は、古代ギリシアの博学者アルキメデスにより書かれた現存する主要な著作の1つと考えられている。この著作は、アルキメデスがアレクサンドリア図書館の館長であるエラトステネスに宛てた手紙の形をとっており[1]、最初に記録された不可分(ときどきこれは無限小と呼ばれる)の明白な使用を含んでいる[1][2]。この著作は元々は失われたと考えられていたが、1906年に有名な『アルキメデス・パリンプセスト』において再発見された。アルキメデスが初めて実証したてこの原理と、多くの特殊な形状において発見した質量中心(もしくは幾何中心)に依拠していることから、いわゆる「機械的方法」("mechanical method")が含まれている。
アルキメデスは厳密な数学の一部として不可分の方法を認めていなかったため、その結果を含む正式な論文ではこの方法を発表しなかった。これらの論文の中では、同じ定理を取り尽くし法により証明し、求める答えに収束する厳密な上界と下界を見つけている。それにもかかわらず、この機械的方法は彼がのちに厳密な証明を与える関係を発見するために使われたものであった。
放物線の面積
[編集]今日、アルキメデスの方法を説明するには、もちろん当時は使うことができなかったがデカルト幾何学を少し使うと便利である。アルキメデスの考えはてこの原理を用いて他の図形の既に知っている質量中心から図形の面積を求めるというものである。最も単純な例は放物線の面積である。アルキメデスはもっとエレガントな方法を使っているが、デカルトの方法では次の積分を計算する。
これは現在では初歩的な積分を使うことで簡単に確認することができる。
アルキメデスのアイデアは、放物線(上積分される曲がった領域)と同じ材料で作られた三角形と機械的に均衡をとるというものである。放物線はx-y平面内でxが0から1に変化したときのx軸とy = x2の間の領域である。三角形はx-y平面内でxが0から1に変化したときのx軸とy = xの間の領域である。
放物線と三角形をxの値ごとに1つずつ垂直にスライスする。x軸がてこであり、支点がx=0にあると考える。てこの原理は支点の反対側にある2つの物体が、それぞれ同じトルクを持っている場合に均衡となることを言っている。このときの物体のトルクは、その物体の質量と支店からの距離の積に等しい。xの各値について、xの位置にある三角形のスライスは、その高さxに等しい質量を持ち、支点からの距離xのところにある。よって、高さx2の放物線のスライスを支点から反対側で距離1のx = −1に移すと、均衡をとることになる。
それぞれのスライスのペアが均衡をとるため、放物線全体をx = −1に移動させると、三角形全体が均衡をとることになる。これはカットされていない元の放物線を点x = −1からフックで吊るすと(その点に放物線の全質量を取り付けると)、x = 0 と x = 1の間にある三角形と均衡をとることができることを意味する。
三角形の質量中心は、アルキメデスにより次の方法で簡単に求めることができる。中線が三角形のいずれかの頂点から反対側の辺Eに引かれる場合、三角形は支点とみなされる中点で釣り合う。その理由は、三角形がEに平行な無限小の線分に分割される場合、各線分は中線の反対側で等しい長さを持ち、対称性により均衡する。この議論は無限小である線の代わりに小さな長方形を使う取り尽くし法により簡単に厳密なものにすることができ、これはアルキメデスが『平面の釣合について』で行っている。
したがって、三角形の質量中心は中線上の交点にあるはずである。問題の三角形の場合、1つの中線はy = x/2で、2番目の中線はy = 1 − xである。これらの方程式を解くと、2つの中線の交点はx = 2/3である点上にあることがわかり、てこ上における三角形の総質量は、三角形の総質量がこの点を押し下げている(もしくはぶら下がっている)かのようになる。三角形による総トルクはその面積1/2にx = 0にある支点から質量中心までの距離2/3をかけたものである。この1/3のトルクは支点から距離-1にある放物線の均衡をとる。したがって、放物線の面積は逆のトルクを与えるために1/3でなければならない。
このような方法で放物線の任意の断面積を求めることができ、同様の議論でxの任意乗の積分を求めることができるが、これ以上の乗数は代数学を使わないと複雑になる。アルキメデスは半球の質量中を求めるために使ったx3の積分までしか行っていないが、他の作品では放物線の質量中心を求めている。
パリンプセストの最初の命題
[編集]右図の放物線を考える。放物線上の2つの点を選び、それぞれAとBとする。
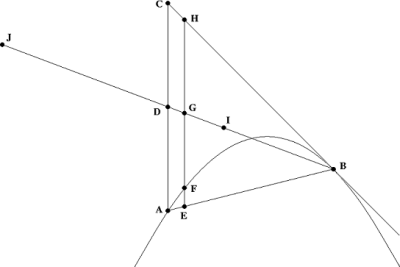
線分ACが放物線の対称軸に平行であるとする。さらに線分BCがBで放物線に接する線上にあるとすると、最初の命題は次のようになる。
- 三角形ABCの面積は、放物線と割線ABで囲まれる領域の面積のちょうど3倍である。
- 証明:
DをACの中点とする。JからDまでの距離がBからDまでの距離と等しくなるように、Dを通る線分JBを作る。ここでは線分JBをDを支点とする「てこ」と考える。アルキメデスがそれより前に示したように、三角形の質量中心はDI :DB = 1:3である「てこ」上の点Iにある。それゆえ、三角形の内側の全重量がIに、放物線の全重量がJにある場合、てこが均衡状態にあることを示せば十分である。
点HがBC上にあり、点EがAB上にあり、放物線の対称軸に平行である線分HEにより与えられる三角形の無限に小さい断面を考える。HEと放物線の交点をF、HEとてこの交点をGとする。三角形の全重量がIにかかれば、HEにかかっているのと同じトルクがてこJBにかかる。したがって、断面HEの重量がGに、放物線の断面EFの重量がJにある場合、てこが均衡状態にあることを示したい。言い換えればEF :GD = EH :JDであることを示せば十分である。しかし、これは放物線の方程式から機械的操作で求まることである。 Q.E.D.
球の体積
[編集]ここでも機械的な方法を説明するために、少しばかり座標幾何を使うと便利である。半径1の球の中心をx = 1とすると、0から2の間の任意のxにおける垂直の断面の半径は次の式で与えられる。
てこで均衡をとるために、この断面の質量は面積に比例するとする。
アルキメデスは、y = 0とy = xとx = 2に囲まれた三角形の領域をx軸を中心として回転させて円錐を作ることを考えた。この円錐の断面は半径の円となる。
すると、この断面積の面積は
となる。そのため、円錐と球両方のスライスを一緒に計量する場合、結合した断面積は
となる。2つのスライスを支点から距離1で一緒に配置した場合、総重量は反対側で支点からの距離xで面積の円によりちょうど均衡となる。これは、すべてをx = 1に移動させれば反対側の底面の半径1で高さ2の円柱で均衡がとれることを意味する。
xは0から2まで範囲であるため、円柱の重心は支点から1の距離にあり、円柱の重さはすべて1の位置にあると考えることができる。均衡の条件は、円錐の体積に球の体積を加えたものが円柱の体積と等しくなることを保証するものである。
円柱の体積は断面積と高さ2を掛け算してとなる。アルキメデスは、円錐の体積も機械的方法で求めることができた。現代的な用語を使えば、関係する積分は放物線の面積の積分と全く同じである。円錐の体積は底面の面積に高さをかけて、それに1/3をかけたものである。円錐の底面は半径2の円であり、面積はである。高さは2であるため体積はとなる。円柱の体積から円錐の体積を引き算すると球の体積となる。
球の体積が半径に依存していることはスケーリングから明らかであるが、当時はそれを厳密にするのは簡単なことではなかった。この方法では球の体積のおなじみの公式が得られる。アルキメデスは寸法を線形にスケーリングすることで、簡単に体積の結果を回転楕円体に拡大した。
アルキメデスの議論は上記の議論とほぼ同じであるが、円柱の半径はもっと大きかったため、円錐と円柱は支点からより長い距離で吊り下げられていた。アルキメデスはこの議論を自身の最大の成果と考え、自身の墓石に均衡状態にある球、円錐、円柱の図を刻むようお願いしていた。
球の表面積
[編集]球の表面積を求めるために、アルキメデスは円の面積が円周を回る無限に多くの無限小の直角三角形と考えられるように(円周の測定参照)、球の体積は表面積を底面とし半径に等しい高さを持つ多くの円錐に分割されていると考えることができる。円錐の高さはすべて同じであるため、体積は表面積に高さと1/3をかけたものになる。
アルキメデスは球の総体積は底面の面積が球の表面積と等しく、高さが半径である円錐の体積に等しいと言っている。議論の詳細は述べられていないが、明らかな理由は円錐は底面の面積を分割することで無限小の円錐に分割することができ、それぞれの円錐は球と同じように底面積に応じて寄与しているからである。
球の表面積を Sとすると、底面積がSで高さがrの円錐の体積はとなり、球の体積と等しくなければならない。ゆえに球の表面積は、「最大の円の4倍」でなければならない。アルキメデスはこのことを『球と円柱について』で厳密に証明している。
有理数の体積を持つ曲線形状
[編集]『方法』の注目すべき点の1つは、アルキメデスが円柱の断面で定義される2つの図形を発見したことであるが、その図形は曲線的な境界を持つにもかかわらず体積に πが含まれない。これはこの研究の中心となる点である—幾何学的な立体の交点により定義された体積の間には非自明な有理数の関係があるように、ある種の曲線形状は定規とコンパスにより修正することができる。
アルキメデスはこのことを論文の冒頭で強調しており、読者に他の方法で結果を再現することを勧めている。他の例とは異なり、これらの図形の体積はアルキメデスの他の作品では厳密に計算されていない。パリンプセストの断片からは、詳細は保存されていないが、体積の厳密な境界線を証明するために形を刻んだり囲んだりした様子がみられる。
アルキメデスが考える2つの図形は、2つの円柱が直角に交わるものであり、(x, y, z)の領域は次に従う。
- (2Cyl)
円形のプリズムの領域は次に従う。
- (CirP)
どちらの問題も機械的方法では簡単な積分が得られるスライスがある。円形のプリズムの場合はx軸をスライスする。y-z平面上の任意のxにおける領域は、辺長で面積の直角三角形であり、総体積は
- (CirP)
となる。これは機械的方法で簡単に修正できる。それぞれの三角形の暗面に面積の三角錐の断面をそれぞれ加えると、断面が一定のプリズムが均衡となる。
2つの円柱の交点の場合は、写本の中ではスライスが失われているが、残りの部分と並行して明白な方法で再構成することができる。x-z平面をスライス方向とすると、円柱の方程式はかつとなる。これはx-z平面において1辺の長さがである正方形の領域を定義している。よって総体積は
- (2Cyl)
となる。これは先に出てきた例と同じ積分である。
パリンプセストの他の命題
[編集]幾何学の一連の命題は、パリンプセストでも同様の議論により証明されている。1つの定理は半球の質量中心の位置は、球の極から中心までの線の5/8の位置にあるというものである。この問題は3次積分を評価していることから注目すべき問題である。
関連項目
[編集]脚注
[編集]- ^ a b Archimedes 1912
- ^ Netz, Reviel; Saito, Ken; Tchernetska, Natalie: A new reading of Method Proposition 14: preliminary evidence from the Archimedes palimpsest. I. SCIAMVS 2 (2001), 9–29.

























