利用者:Meniv/Needleman–Wunsch アルゴリズム

Needleman–Wunsch アルゴリズム（ニードルマン・ブンシュ アルゴリズム）とは動的計画法によるアルゴリズムの一つでバイオインフォマティクスの分野で用いられる。タンパク質（プロテイン）や核様体（ヌクレオイド）の配列をアラインメントする際に用いられ, 1970年にSaul B. NeedlemanとChristian D. Wunschによって開発された。時に最適マッチングやグローバルアラインメントのアルゴリズムとしても用いられる。

Figure 1: Needleman-Wunsch ペアワイズシーケンスアラインメント

Sequences    Best Alignments
---------    ----------------------
GATTACA      G-ATTACA      G-ATTACA      G-ATTACA
GCATGCU      GCATG-CU      GCA-TGCU      GCAT-GCU

基本的なアルゴリズム

Needleman–Wunsch アルゴリズムは2つの文字列のアラインメントを行う。ここではDNA配列として以下の2つを用いることとする:

GCATGCU
GATTACA

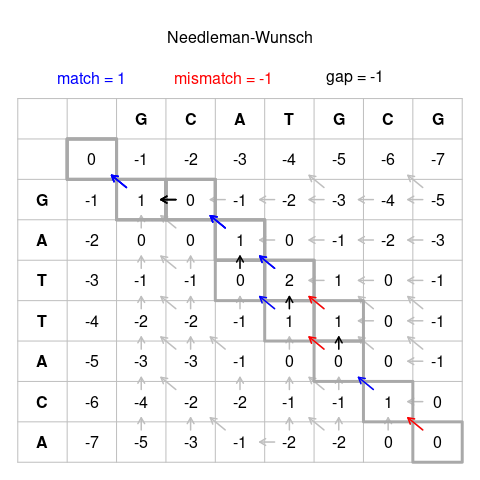
1.グリッドの組み立て Figure 1のような表を書く。文字列（配列）の長さ+2を縦横にもつ表を書き、一方を左上から下に3マス目から書き他方を左上から右に3マス目から書いていく。この時点ではまだ数値は書かない。

2.得点システムの決定 どのように採点を行うかを定める。それぞれの文字は以下のような状態を取るものとする

• Match: 2つの文字は等しい
• Mismatch: 2つの文字は異なる
• Indel (INsertion or DELetion) : 片方の文字がもう片方の文字の位置との間にズレがある

Figure 1の例ではMatchで+1点、Mismatchで-1点、Indel(gap)で-1点を得ると定めている。

3.表を埋める 左上のマスから斜め下に下がったマスから始める。この最初のマスには0を記入する。次に隣（下あるいは右）のマスへ移動しマスの値を計算していく。mismatchに相当するので、上あるいは左のマスの得点より-1ずつ小さくなっていく。

		G	C	A	T	G	C	U
	0	-1	-2	-3	-4	-5	-6	-7
G	-1
A	-2
T	-3
T	-4
A	-5
C	-6
A	-7

次にスコア0を埋めたマスの右下のマスを埋める。?にはいる得点は、0のマス、0を埋めた下のマス、0を埋めた右のマスにある3つの得点から算出する。

		G
	0	-1
G	-1	?

As for all following cells, we have three options here. Firstly the score could be calculated from the existing score on top. In this case we would add -1 as this represents an indel, resulting in a total of -2. The same applies if we calculate from the existing score to the left. Calculating from the diagonal (top-left) existing score represents two letters aligned together. If the letters are the same this is a match, otherwise it is a mismatch. In this case the bases match and so we add +1. So we have -2, -2 and +1 as possible scores to choose from. The diagonal score is the best score so we give the cell a score of 1. We also need to keep track of where the score came from, shown as an arrow in the completed figure. Below shows samples from our example where the best score comes from the left and top cells respectively.

	G	C
	-1	-2
G	1	0

	C	A
A	0	1
T	-1	0

In some cells 2 or even all 3 of the originating cells may result in equal best scores such as this segment of figure x:

	T	G
T	1	1
A	0	0

Here we can see that the score of zero is obtained both from the top cell and the top-left cell (both are 1 – 1=0). This represents the branching of two equally good alignments. In this scenario we need to fill in arrows to both cells. Follow this procedure for all the remaining cells until the table is filled.

The score in the last cell (bottom right) represents the alignment score for the best alignment.

Trace Arrows back to origin

Note that there are multiple equally 'best' alignments, here we show just one.

Follow the arrows back to the original cell to obtain the path for the best alignment. Then follow the path from start to finish to construct the alignment based on these rules

• A diagonal arrow represents a match or mismatch, either way this means each letter corresponds to another letter. For example the first arrow represents:

Nothing --> G
Nothing --> G

• If there is a horizontal arrow there will be two columns for one row in the alignment and hence a gap in the side string. This gap is after the letter in the row. For example the second arrow represents:

G --> GC
G --> G-

• If there is a vertical arrow there will be two rows for one column in the alignment and hence a gap in the top string. This gap is after the letter in the column. For example the forth arrow represents:

GCA --> GCA-
G-A --> G-AT

• Note how there are multiple 'forth' arrows to choose from, these represent branching of the alignments. If these branches return the last cell with the same score then they are equally viable alignments

Following these rules one possible alignment is constructed as follows:

G →  GC → GCA → GCA- → GCA-T → GCA-TG → GCA-TGC →  GCA-TGCU
G →  G- → G-A → G-AT → G-ATT → G-ATTA → G-ATTAC →  G-ATTACA

Historical notes and algorithm development

The original purpose of the algorithm described by Needleman and Wunsch was to find similarities in the amino acid sequences of two proteins.

Needleman and Wunsch describe their algorithm explicitly for the case when the alignment is penalized solely by the matches and mismatches, and gaps have no penalty (d=0). The original publication from 1970 suggests the recursion $F_{ij}=\max _{h<i,k<j}\{F_{h,j-1}+S(A_{i},B_{j}),F_{i-1,k}+S(A_{i},B_{j})\}$.

The corresponding dynamic programming algorithm takes cubic time. The paper also points out that the recursion can accommodate arbitrary gap penalization formulas:

A penalty factor, a number subtracted for every gap made, may be assessed as a barrier to allowing the gap. The penalty factor could be a function of the size and/or direction of the gap. [page 444]

A better dynamic programming algorithm with quadratic running time for the same problem (no gap penalty) was first introduced by David Sankoff in 1972. Similar quadratic-time algorithms were discovered independently by T. K. Vintsyuk in 1968 for speech processing ("time warping"), and by Robert A. Wagner and Michael J. Fischer in 1974 for string matching.

Needleman and Wunsch formulated their problem in terms of maximizing similarity. Another possibility is to minimize the edit distance between sequences, introduced by Vladimir Levenshtein. Peter H. Sellers showed in 1974 that the two problems are equivalent.

The Needleman–Wunsch algorithm is still widely used for optimal global alignment, particularly when the quality of the global alignment is of the upmost importance. However, the algorithm is expensive with respect to time and space, proportional to the product of the length of two sequences and hence is not suitable for long sequences.

Recent development has focused on improving the time and space cost of the algorithm while maintaining quality. For example, in 2013, a Fast Optimal Global Sequence Alignment Algorithm (FOGSAA), suggested alignment of nucleotide/protein sequences faster than other optimal global alignment methods, including the Needleman–Wunsch algorithm. The paper claims that when compared to the Needleman–Wunsch algorithm, FOGSAA achieves a time gain of 70–90% for highly similar nucleotide sequences (with > 80% similarity), and 54–70% for sequences having 30–80% similarity.

Global Alignment Tools using Needleman-Wunsch algorithm

• EMBOSS Needle and EMBOSS Stretcher Global Alignment Tools
• Needleman-Wunsch alignment for two nucleotide sequences
• MathWorks - Globally align two sequences using Needleman-Wunsch algorithm

See also

• Smith-Waterman algorithm
• Sequence mining
• Levenshtein distance
• Dynamic time warping

External links

• NW-align: A protein sequence-to-sequence alignment program by Needleman-Wunsch algorithm (online server & source code)
• Needleman-Wunsch Algorithm as Ruby Code
• Needleman-Wunsch Algorithm as Haskell Code
• A live Javascript-based demo of Needleman-Wunsch
• B.A.B.A. — an applet (with source) which visually explains the algorithm.
• A clear explanation of NW and its applications to sequence alignment
• Sequence Alignment Techniques at Technology Blog
• OPAL JavaScript implementation of algorithms: Needleman-Wunsch, Needleman-Wunsch-Sellers and Smith-Waterman
• Biostrings R package implementing Needleman–Wunsch algorithm among others
• Parallel Needleman-Wunsch Algorithm for Grid Implementation by Tahir Naveed, Imitaz Saeed Siddiqui, Shaftab Ahmed - Bahria University
• Needleman-Wunsch Algorithm as Haxe Code