利用者:Jikken-Joe/sandbox

ここはJikken-Joeさんの利用者サンドボックスです。編集を試したり下書きを置いておいたりするための場所であり、百科事典の記事ではありません。ただし、公開の場ですので、許諾されていない文章の転載はご遠慮ください。

登録利用者は自分用の利用者サンドボックスを作成できます（サンドボックスを作成する、解説）。

転位（てんい、英語: dislocation）は、材料科学の用語で、結晶中に含まれる、線状の結晶欠陥のことである。外力等によって、転位近傍の原子が再配置されることによって転位の位置が移動し、材料が変形するため、変形に要する力は原子間の結合力から理論的に計算される力よりも小さく、金属の硬さ（変形のしにくさ）は、転位の動きやすさが決めている。転位が動くことによって、金属等は外力に対して、破壊せずに変形する塑性変形を起こす。このようなメカニズムをエゴン・オロワン（英語版）らが解明することによって結晶力学は飛躍的に進歩し塑性変形強度の基本原理となった。

分類

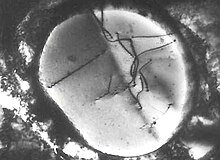
転位線の周りの原子の不一致の向きはバーガースベクトルで表される。転位は、転位線とバーガースベクトルの関係により以下のように分類される。

刃状転位: （じんじょうてんい、はじょうてんい、英: edge dislocation）; 転位線とバーガースベクトルが垂直で、転位のない結晶に余分面を無理やり押しこんだ形の結晶欠陥である。
螺旋転位: （らせんてんい、英: screw dislocation）; 転位線とバーガースベクトルが平行で、転位線に対して平行に結晶面がずれているものをいう。
混合転位: 転位線とバーガースベクトルが平行でも垂直でもなく、刃状転位と螺旋転位の2つが混合し両方の性質をもっている。

性質

転位は結晶の内部で端点を持つことができず、ループ状になるか端点が結晶表面に出てこなくてはならない^[1]。

転位密度（単位体積当たりの転位線の長さ）は普通の金属において、焼きなました状態で10¹⁰ - 10¹² m^-2 程度、塑性加工して10¹⁴ - 10¹⁶ m^-2 程度である^[1]。

転位の周りには弾性ひずみ場が存在するためエネルギー的に高い状態にある。このため、転位線にはその長さを短くしようとする張力がはたらく。転位のエネルギー $E$ （これは張力の大きさに等しい）はバーガースベクトル $b$ を用いて次式で表される^[1]。

E\simeq {\frac {1}{2}}Gb^{2}

ここで $G$ は剛性率である。またこのエネルギーのため、近くにある転位の間には相互作用がはたらく。たとえば符号の異なる2つの刃状転位の間にはそれらを結ぶ方向に引力がはたらく。

せん断強度との関係

1930年代に、材料の理論的せん断強度をオロワンが求めている。

\tau _{m}={\frac {G}{2\pi }}

ここで、Gは剛性率、τ_mはせん断強度である。

金属の剛性率が約20-150 GPaであるため理論的せん断強度は数～数10 GPaとなるのに対し、実際のせん断強度は 0.5-10 MPaにすぎない。オロワンらによって金属の転位の概念が導入された。これにより、金属結晶の強度の議論が理論的に可能になり、さらにはその後確立された「破壊力学」とセットにした材料強度学への発展と繋がっている。

せん断による塑性変形を転位に運動によるとし、せん断強度を再評価すると

\tau _{m}={\frac {2G}{1-\nu }}\exp \left(-{\frac {2\pi a}{(1-\nu )b}}\right)

で与えられ、実際の変形に要する応力に近くなる^[2]。ここで $ν$ はポアソン比、 $b$ はバーガースベクトル、 $a$ はすべり面の原子間距離である。この $τ m$ をパイエルス・ナバロ応力という。

運動、増殖機構

すべり面

転位は結晶内を自由に移動できるわけではなく、結晶構造や原子配列による制限を受ける。

具体的には、転位線とバーガースベクトルを共に含む平面（すべり面）内に移動が制限される。刃状転位や混合転位は、バーガースベクトルが転位線と異なる向きなので、すべり面は一意的に決まる。一方、螺旋転位はバーガースベクトルが転位線に沿った向きなので、転位線を含む任意の平面がすべり面になり得る。^[3]

上昇運動と交差すべり

刃状転位及び混合転位は、外力の作用だけでは、その転位固有のすべり面上しか移動することができない。そのすべり面を逸脱して移動（上昇運動）するためには、転位を含む部分での原子の拡散が必要となる。

一方で螺旋転位は、転位線を含む複数の平面がすべり面の候補になることから、例えばあるすべり面S₁を移動する転位を考えると、その転位がS₁と交わる別のすべり面S₂に乗り移って移動することもできる（ただし、S₁とS₂との交線は転位線と平行でなければならない）。このような現象を交差すべりという。^[4]

転位の増殖（フランク＝リード源）

あるすべり面上に、有限の長さ（線分）でかつその両端がピン止めされている転位を考える。これは例えば、湾曲した転位で、一部螺旋転位と

脚注

^ ^a ^b ^c 駒井、p.20
^ 駒井、p.28
^ 木村. pp. 58-59.
^ 木村. pp. 60-61.

参考文献

駒井謙治郎編『機械材料学』（9版）日本材料学会、1999年。
木村宏『改訂　材料強度の考え方』アグネ技術センター、2002年。

分類

性質