利用者:Einstee/sandbox

ここはEinsteeさんの利用者サンドボックスです。編集を試したり下書きを置いておいたりするための場所であり、百科事典の記事ではありません。ただし、公開の場ですので、許諾されていない文章の転載はご遠慮ください。

登録利用者は自分用の利用者サンドボックスを作成できます（サンドボックスを作成する、解説）。

エアマス係数（（えあますけいすう、air mass coefficient）は、地球大気を通過する直達光の長さと定義され、上向き垂直方向の経路長（すなわち、天頂）に対する相対的な比として示される。エアマス係数は、太陽放射が大気を通過した後、その太陽スペクトラムの特徴を説明する助けとして利用可能である。エアマス係数は、標準常態下の太陽電池の性能を説明する為に一般的に使用され、しばしば"AM"と"数字"を用いて表す。 "AM1.5"は、陸上の太陽電池パネルの特徴を説明する際に、ほぼ世界共通で用いられる。

The air mass coefficient defines the direct optical path length through the Earth's atmosphere, expressed as a ratio relative to the path length vertically upwards, i.e. at the zenith. The air mass coefficient can be used to help characterize the solar spectrum after solar radiation has traveled through the atmosphere. The air mass coefficient is commonly used to characterize the performance of solar cells under standardized conditions, and is often referred to using the syntax "AM" followed by a number. "AM1.5" is almost universal when characterizing terrestrial power-generating panels.

概要 (Description)

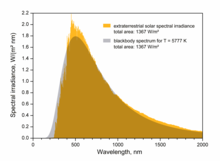
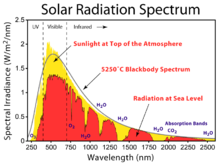
太陽放射は、5,800 Kにおける黒体放射とよく一致する^[1]。大気を通過する事により、太陽光は散乱や吸収により減衰する（太陽光の通過する大気が厚くなるほど、より減衰も増す）。

Solar radiation closely matches a black body radiator at about 5,800 K.^[1] As it passes through the atmosphere, sunlight is attenuated by scattering and absorption; the more atmosphere through which it passes, the greater the attenuation.

太陽光が大気と通過する際、化学物質と相互に作用し、特定の波長で吸収が起こる。おそらく最も良く知られている例として、大気上層のオゾンによる紫外線の吸収であり、地表面に到達する短波長の光の量を劇的に減少させる。この過程のより激しい要素として水蒸気があり、窒素、酸素と二酸化炭素分子がこの過程に加わりながら、多くの波長で多種多様な吸収帯が生じる。太陽光が地表に到達するまでに、スペクトルは遠赤外から近紫外の範囲に強く制限される。
As the sunlight travels through the atmosphere, chemicals interact with the sunlight and absorb certain wavelengths. Perhaps the best known example is the stripping of ultraviolet light by ozone in the upper atmosphere, which dramatically reduces the amount of short-wavelength light reaching the Earth's surface. A more active component of this process is water vapor, which results in a wide variety of absorption bands at many wavelengths, while molecular nitrogen, oxygen and carbon dioxide add to this process. By the time it reaches the Earth's surface, the spectrum is strongly confined between the far infrared and near ultraviolet.

大気は、太陽直達光から高い周波数を取り除いたり、空に対して太陽直達光を散乱する役割を果たす^[2]。空が青く写り、太陽が黄色い理由は、これによる。より周波数の高い青い光は、間接的に散乱を通して観測者に届く。また、青より小さい光は直達路に沿って進み、太陽に黄色みがかった色を与える^[3]。太陽光が通過する大気の距離が長いほど、この影響はより強くなり、太陽光が大気を大きく斜いて通る日の出と日没時に、太陽が赤やオレンジに見える理由である。なぜなら、累積的により多くの青と緑の光が直達光より取り除かれ、太陽に赤やオレンジの見ためを与えるからである。そして同時に、空はピンクに見える。なぜなら、青と緑の光が観測者に届く前に、そのような長い経路で大きく減衰される上に散乱されるからであり、結果として日の入りと日の出において空がピンクの特徴を示すことになる。
Atmospheric scattering plays a role, removing higher frequencies from direct sunlight and scattering it about the sky.^[4] This is why the sky appears blue and the sun yellow — more of the higher-frequency blue light arrives at the observer via indirect scattered paths; and less blue light follows the direct path, giving the sun a yellow tinge.^[5] The greater the distance in the atmosphere through which the sunlight travels, the greater this effect, which is why the sun looks orange or red at dawn and sundown when the sunlight is travelling very obliquely through the atmosphere — progressively more of the blues and greens are removed from the direct rays, giving an orange or red appearance to the sun; and the sky appears pink — because the blues and greens are scattered over such long paths that they are highly attenuated before arriving at the observer, resulting in characteristic pink skies at dawn and sunset.

定義 (Definition)

大気を通過する経路長 $L$ 、地表面に対する垂直な線 For a path length $L$ through the atmosphere, for solar radiation incident at angle $z$ relative to the normal to the Earth's surface, the air mass coefficient is:^[6]

AM={\frac {L}{L_{\mathrm {o} }}}\approx {\frac {1}{\cos \,z}}\,

(A.1)

where $L_{\mathrm {o} }$ is the zenith path length (i.e. normal to the Earth's surface) at sea level and $z$ is the zenith angle in degrees.

The air mass number is thus dependent on the Sun's elevation path through the sky and therefore varies with time of day and with the passing seasons of the year, and with the latitude of the observer.

Accuracy near the horizon

The above approximation overlooks the curvature of the Earth, and is reasonably accurate for values of $z$ up to around 75°. A number of refinements have been proposed to more accurately model the path thickness towards the horizon, such as that proposed by Kasten and Young (1989):^[7]

AM={\frac {1}{\cos \,z+0.50572\,(96.07995-z)^{-1.6364}}}\,

(A.2)

A more comprehensive list of such models is provided in the main article Airmass, for various atmospheric models and experimental data sets. At sea level the air mass towards the horizon ( $z$ = 90°) is approximately 38.^[8]

Modelling the atmosphere as a simple spherical shell provides a reasonable approximation:^[9]

AM={\sqrt {(r\cos z)^{2}+2r+1}}\;-\;r\cos z\,

(A.3)

where the radius of the Earth $R_{\mathrm {E} }$ = 6371 km, the effective height of the atmosphere $y_{\mathrm {atm} }$ ≈ 9 km, and their ratio $r=R_{\mathrm {E} }/y_{\mathrm {atm} }$ ≈ 708.

These models are compared in the table below:

Estimates of airmass coefficient at sea level
$z$	Flat Earth	Kasten & Young	Spherical shell
degree	(A.1)	(A.2)	(A.3)
0°	1.0	1.0	1.0
60°	2.0	2.0	2.0
70°	2.9	2.9	2.9
75°	3.9	3.8	3.8
80°	5.8	5.6	5.6
85°	11.5	10.3	10.6
88°	28.7	19.4	20.3
90°	$\infty$	37.9	37.6

This implies that for these purposes the atmosphere can be considered to be effectively concentrated into around the bottom 9 km,^[10] i.e. essentially all the atmospheric effects are due to the atmospheric mass in the lower half of the Troposphere. This is a useful and simple model when considering the atmospheric effects on solar intensity.

Cases

AM0

The spectrum outside the atmosphere, approximated by the 5,800 K black body, is referred to as "AM0", meaning "zero atmospheres". Solar cells used for space power applications, like those on communications satellites are generally characterized using AM0.

AM1

The spectrum after travelling through the atmosphere to sea level with the sun directly overhead is referred to, by definition, as "AM1". This means "one atmosphere". AM1 ( $z$ =0°) to AM1.1 ( $z$ =25°) is a useful range for estimating performance of solar cells in equatorial and tropical regions.

AM1.5

Solar panels do not generally operate under exactly one atmosphere's thickness: if the sun is at an angle to the Earth's surface the effective thickness will be greater. Many of the world's major population centres, and hence solar installations and industry, across Europe, China, Japan, the United States of America and elsewhere (including northern India, southern Africa and Australia) lie in temperate latitudes. An AM number representing the spectrum at mid-latitudes is therefore much more common.

"AM1.5", 1.5 atmosphere thickness, corresponds to a solar zenith angle of $z$ =48.2°. While the summertime AM number for mid-latitudes during the middle parts of the day is less than 1.5, higher figures apply in the morning and evening and at other times of the year. Therefore AM1.5 is useful to represent the overall yearly average for mid-latitudes. The specific value of 1.5 has been selected in the 1970s for standardization purposes, based on an analysis of solar irradiance data in the conterminous United States.^[11] Since then, the solar industry has been using AM1.5 for all standardized testing or rating of terrestrial solar cells or modules, including those used in concentrating systems. The latest AM1.5 standards pertaining to photovoltaic applications are the ASTM G-173^[12]^[13] and IEC 60904, all derived from simulations obtained with the SMARTS code

AM2~3

AM2 ( $z$ =60°) to AM3 ( $z$ =70°) is a useful range for estimating the overall average performance of solar cells installed at high latitudes such as in northern Europe. Similarly AM2 to AM3 is useful to estimate wintertime performance in temperate latitudes, e.g. airmass coefficient is greater than 2 at all hours of the day in winter at latitudes as low as 37°.

AM38

AM38 is generally regarded as being the airmass in the horizontal direction ( $z$ =90°) at sea level.^[8] However, in practice there is a high degree of variability in the solar intensity received at angles close to the horizon as described in the next section Solar intensity.

At higher altitudes

The relative air mass is only a function of the sun's zenith angle, and therefore does not change with local elevation. Conversely, the absolute air mass, equal to the relative air mass multiplied by the local atmospheric pressure and divided by the standard (sea-level) pressure, decreases with elevation above sea level. For solar panels installed at high altitudes, e.g. in an Altiplano region, it is possible to use a lower absolute AM numbers than for the corresponding latitude at sea level: AM numbers less than 1 towards the equator, and correspondingly lower numbers than listed above for other latitudes. However, this approach is approximate and not recommended. It is best to simulate the actual spectrum based on the relative air mass (e.g., 1.5) and the actual atmospheric conditions for the specific elevation of the site under scrutiny.

Solar intensity

Solar intensity at the collector reduces with increasing airmass coefficient, but due to the complex and variable atmospheric factors involved, not in a simple or linear fashion. For example, almost all high energy radiation is removed in the upper atmosphere (between AM0 and AM1) and so AM2 is not twice as bad as AM1. Furthermore there is great variability in many of the factors contributing to atmospheric attenuation,^[14] such as water vapor, aerosols, photochemical smog and the effects of temperature inversions. Depending on level of pollution in the air, overall attenuation can change by up to ±70% towards the horizon, greatly affecting performance particularly towards the horizon where effects of the lower layers of atmosphere are amplified manyfold.

One approximate model for solar intensity versus airmass is given by:^[15] ^[16]

I=1.1\times I_{\mathrm {o} }\times 0.7^{(AM)^{(0.678)}}\,

(I.1)

where solar intensity external to the Earth's atmosphere $I_{\mathrm {o} }$ = 1.353 kW/m², and the factor of 1.1 is derived assuming that the diffuse component is 10% of the direct component.^[15]

This formula fits comfortably within the mid-range of the expected pollution-based variability:

Solar intensity vs zenith angle $z$ and airmass coefficient AM
$z$	AM	range due to pollution^[14]	formula (I.1)	ASTM G-173^[13]
degree		W/m²	W/m²	W/m²
-	0	1367^[17]	1353	1347.9^[18]
0°	1	840 .. 1130 = 990 ± 15%	1040
23°	1.09	800 .. 1110 = 960 ± 16%^[19]	1020
30°	1.15	780 .. 1100 = 940 ± 17%	1010
45°	1.41	710 .. 1060 = 880 ± 20%^[19]	950
48.2°	1.5	680 .. 1050 = 870 ± 21%^[19]	930	1000.4^[20]
60°	2	560 .. 970 = 770 ± 27%	840
70°	2.9	430 .. 880 = 650 ± 34%^[19]	710
75°	3.8	330 .. 800 = 560 ± 41%^[19]	620
80°	5.6	200 .. 660 = 430 ± 53%	470
85°	10	85 .. 480 = 280 ± 70%	270
90°	38		20

This illustrates that significant power is available at only a few degrees above the horizon.

At higher altitudes

One approximate model for intensity increase with altitude and accurate to a few kilometres above sea level is given by:^[15] ^[21]

I=1.1\times I_{\mathrm {o} }\times [(1-h/7.1)0.7^{(AM)^{0.678})}+h/7.1]\,

(I.2)

where $h$ is the solar collector's height above sea level in km and $AM$ is the airmass (from A.2) as if the collector was installed at sea level.

Alternatively, given the significant practical variabilities involved, the homogeneous spherical model could be applied to estimate AM, using:

AM={\sqrt {(r+c)^{2}\cos ^{2}z+(2r+1+c)(1-c)}}\;-\;(r+c)\cos z\,

(A.4)

where the normalized heights of the atmosphere and of the collector are respectively $r=R_{\mathrm {E} }/y_{\mathrm {atm} }$ ≈ 708 (as above) and $c=h/y_{\mathrm {atm} }$ .

And then the above table or the appropriate equation (I.1 or I.3 or I.4 for average, polluted or clean air respectively) can be used to estimate intensity from AM in the normal way.

These approximations at I.2 and A.4 are suitable for use only to altitudes of a few kilometres above sea level, implying as they do reduction to AM0 performance levels at only around 6 and 9 km respectively. By contrast much of the attenuation of the high energy components occurs in the ozone layer - at higher altitudes around 30 km.^[22] Hence these approximations are suitable only for estimating the performance of ground based collectors.

Solar cell efficiency

→詳細は「Solar cell efficiency」を参照

Silicon solar cells are not very sensitive to the portions of the spectrum lost in the atmosphere. The resulting spectrum at the Earth's surface more closely matches the bandgap of silicon so silicon solar cells are more efficient at AM1 than AM0. This apparently counter-intuitive result arises simply because silicon cells can't make much use of the high energy radiation which the atmosphere filters out. As illustrated below, even though the efficiency is lower at AM0 the total output power (P_out) for a typical solar cell is still highest at AM0. Conversely, the shape of the spectrum does not significantly change with further increases in atmospheric thickness, and hence cell efficiency does not greatly change for AM numbers above 1.

Output power vs airmass coefficient
AM	Solar intensity	Output power	Efficiency
	P_in W/m²	P_out W/m²	P_out / P_in
0	1350	160	12%
1	1000	150	15%
2	800	120	15%

This illustrates the more general point that given that solar energy is "free", and where available space is not a limitation, other factors such as total P_out and P_out/$ are often more important considerations than efficiency (P_out/P_in).

Notes and references

^ ^a ^b or more precisely 5,777 K as reported in NASA Solar System Exploration - Sun: Facts & Figures retrieved 27 April 2011 "Effective Temperature ... 5777 K"
^ See also the article Diffuse sky radiation.
^ Yellow is the color negative of blue — yellow is the aggregate color of what remains after scattering removes some blue from the "white" light from the sun.
^ See also the article Diffuse sky radiation.
^ Yellow is the color negative of blue — yellow is the aggregate color of what remains after scattering removes some blue from the "white" light from the sun.
^ Peter Würfel (2005). The Physics of Solar Cells. Weinheim: Wiley-VCH ISBN 3-527-40857-6.
^ Kasten, F. and Young, A. T. (1989). Revised optical air mass tables and approximation formula. Applied Optics 28:4735–4738.
^ ^a ^b The main article Airmass reports values in the range 36 to 40 for different atmospheric models
^ Schoenberg, E. (1929). Theoretische Photometrie, g) Über die Extinktion des Lichtes in der Erdatmosphäre. In Handbuch der Astrophysik. Band II, erste Hälfte. Berlin: Springer.
^ The main article Airmass reports values in the range 8 to 10 km for different atmospheric models
^ Gueymard, C.; Myers, D.; Emery, K. (2002). “Proposed reference irradiance spectra for solar energy systems testing”. Solar Energy 73 (6): 443–467. doi:10.1016/S0038-092X(03)00005-7.
^ Reference Solar Spectral Irradiance: Air Mass 1.5 NREL retrieved 1 May 2011
^ ^a ^b Reference Solar Spectral Irradiance: ASTM G-173 ASTM retrieved 1 May 2011
^ ^a ^b Planning and installing photovoltaic systems: a guide for installers, architects and engineers, 2nd Ed. (2008), Table 1.1, Earthscan with the International Institute for Environment and Development, Deutsche Gesellshaft für Sonnenenergie. ISBN 1-84407-442-0.
^ ^a ^b ^c PVCDROM retrieved 1 May 2011, Stuart Bowden and Christiana Honsberg, Solar Power Labs, Arizona State University
^ Meinel, A. B. and Meinel, M. P. (1976). Applied Solar Energy Addison Wesley Publishing Co.
^ The Earthscan reference uses 1367 W/m² as the solar intensity external to the atmosphere.
^ The ASTM G-173 standard measures solar intensity over the band 280 to 4000 nm.
^ ^a ^b ^c ^d ^e Interpolated from data in the Earthscan reference using suitable Least squares estimate variants of equation I.1:
for polluted air:

$I=1.1\times I_{\mathrm {o} }\times 0.56^{(AM^{0.715})}\,$
(I.3)

for clean air:

$I=1.1\times I_{\mathrm {o} }\times 0.76^{(AM^{0.618})}\,$
(I.4)
^ The ASTM G-173 standard measures solar intensity under "rural aerosol loading" i.e. clean air conditions - thus the standard value fits closely to the maximum of the expected range.
^ Laue, E. G. (1970), The measurement of solar spectral irradiance at different terrestrial elevations, Solar Energy, vol. 13, no. 1, pp. 43-50, IN1-IN4, 51-57, 1970.
^ R.L.F. Boyd (Ed.) (1992). Astronomical photometry: a guide, section 6.4. Kluwer Academic Publishers. ISBN 0-7923-1653-3.

[NASA5777K-1] r more precisely 5,777 K as reported in NASA Solar System Exploration - Sun: Facts & Figures retrieved 27 April 2011 "Effective Temperature ... 5777 K"

[2] See also the article Diffuse sky radiation.

[3] Yellow is the color negative of blue — yellow is the aggregate color of what remains after scattering removes some blue from the "white" light from the sun.

[4] See also the article Diffuse sky radiation.

[5] Yellow is the color negative of blue — yellow is the aggregate color of what remains after scattering removes some blue from the "white" light from the sun.

[6] Peter Würfel (2005). The Physics of Solar Cells. Weinheim: Wiley-VCH ISBN 3-527-40857-6.

[7] Kasten, F. and Young, A. T. (1989). Revised optical air mass tables and approximation formula. Applied Optics 28:4735–4738.

[AM38-8] The main article Airmass reports values in the range 36 to 40 for different atmospheric models

[9] Schoenberg, E. (1929). Theoretische Photometrie, g) Über die Extinktion des Lichtes in der Erdatmosphäre. In Handbuch der Astrophysik. Band II, erste Hälfte. Berlin: Springer.

[10] The main article Airmass reports values in the range 8 to 10 km for different atmospheric models

[Gueymard2002-11] Gueymard, C.; Myers, D.; Emery, K. (2002). “Proposed reference irradiance spectra for solar energy systems testing”. Solar Energy 73 (6): 443–467. doi:10.1016/S0038-092X(03)00005-7.

[NREL-12] Reference Solar Spectral Irradiance: Air Mass 1.5 NREL retrieved 1 May 2011

[G173-13] Reference Solar Spectral Irradiance: ASTM G-173 ASTM retrieved 1 May 2011

[Earthscan-14] Planning and installing photovoltaic systems: a guide for installers, architects and engineers, 2nd Ed. (2008), Table 1.1, Earthscan with the International Institute for Environment and Development, Deutsche Gesellshaft für Sonnenenergie. ISBN 1-84407-442-0.

[PVCDROM-15] PVCDROM retrieved 1 May 2011, Stuart Bowden and Christiana Honsberg, Solar Power Labs, Arizona State University

[Meinel-16] Meinel, A. B. and Meinel, M. P. (1976). Applied Solar Energy Addison Wesley Publishing Co.

[17] The Earthscan reference uses 1367 W/m² as the solar intensity external to the atmosphere.

[18] The ASTM G-173 standard measures solar intensity over the band 280 to 4000 nm.

[interpolation-19] Interpolated from data in the Earthscan reference using suitable Least squares estimate variants of equation I.1:
for polluted air:

$I=1.1\times I_{\mathrm {o} }\times 0.56^{(AM^{0.715})}\,$
(I.3)

for clean air:

$I=1.1\times I_{\mathrm {o} }\times 0.76^{(AM^{0.618})}\,$
(I.4)

[20] The ASTM G-173 standard measures solar intensity under "rural aerosol loading" i.e. clean air conditions - thus the standard value fits closely to the maximum of the expected range.

[21] Laue, E. G. (1970), The measurement of solar spectral irradiance at different terrestrial elevations, Solar Energy, vol. 13, no. 1, pp. 43-50, IN1-IN4, 51-57, 1970.

[22] R.L.F. Boyd (Ed.) (1992). Astronomical photometry: a guide, section 6.4. Kluwer Academic Publishers. ISBN 0-7923-1653-3.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]