利用者:Cobabu/書きかけ

分子軌道

en:Molecular_orbital 15:27, 22 July 2009版より翻訳し，大幅加筆。

(もとの文章開始)

ベンゼンの最低空軌道

分子軌道（ぶんしきどう、Molecular Orbital、通称MO）は分子中の各電子の空間分布を記述する一電子波動関数のことである。分子軌道法において中心的な役割を果たし、電子に対するシュレーディンガー方程式を、一電子近似を用いて解くことによって得られる。

1個の電子の位置ベクトル$\mathbf {r}$の関数であり、$\phi _{i}(\mathbf {r} )$と表される。 一般に複素数である。原子に対する原子軌道に対応するものである。

(もとの文章終了)

In chemistry, a molecular orbital (or MO) is a mathematical function that describes the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The use of the term "orbital" was first used in English by Robert S. Mulliken in 1925 as the English translation of Schrödinger's use of the German word, 'Eigenfunktion'. It has since been equated with the "region" generated with the function. Molecular orbitals are usually constructed by combining atomic orbitals or hybrid orbitals from each atom of the molecule, or other molecular orbitals from groups of atoms. They can be quantitatively calculated using the Hartree-Fock or Self-Consistent Field method.

H₂ 1sσ bonding molecular orbital

Complete acetylene (H–C≡C–H) molecular orbital set

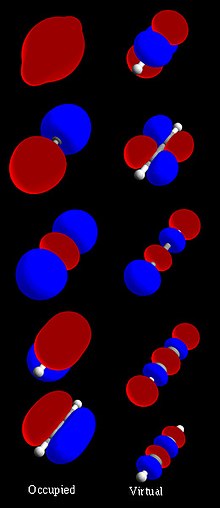
Overview

A molecular orbital (MO) can be used to specify the electron configuration of a molecule: the spatial distribution and energy of one (or one pair of) electron(s). Most commonly an MO is represented as a linear combination of atomic orbitals (the LCAO-MO method), especially in qualitative or very approximate usage. They are invaluable in providing a simple model of bonding in molecules, understood through molecular orbital theory.

Most methods in computational chemistry today start by calculating the MOs of the system. A molecular orbital describes the behavior of one electron in the electric field generated by the nuclei and some average distribution of the other electrons. In the case of two electrons occupying the same orbital, the Pauli principle demands that they have opposite spin. Necessarily this is an approximation, and highly accurate descriptions of the molecular electronic wave function do not have orbitals (see configuration interaction).

Qualitative discussion

For an imprecise, but qualitatively useful, discussion of the molecular structure, the molecular orbitals can be obtained from the "Linear combination of atomic orbitals molecular orbital method" ansatz. In this approach, the molecular orbitals are expressed as linear combinations of atomic orbitals.

Molecular orbitals were first introduced by Friedrich Hund and Robert S. Mulliken in 1927 and 1928. The linear combination of atomic orbitals approximation for molecular orbitals was introduced in 1929 by Sir John Lennard-Jones.. His ground-breaking paper showed how to derive the electronic structure of the fluorine and oxygen molecules from quantum principles. This qualitative approach to molecular orbital theory is part of the start of modern quantum chemistry.

Some properties:

• The number of molecular orbitals is equal to the number the atomic orbitals included in the linear expansion,
• If the molecule has some symmetry, the degenerate atomic orbitals (with the same atomic energy) are grouped in linear combinations (called symmetry adapted atomic orbitals (SO)) which belong to the representation of the symmetry group, so the wave functions that describe the group are known as symmetry-adapted linear combinations (SALC).
• The number of molecular orbitals belonging to one group representation is equal to the number of symmetry adapted atomic orbitals belonging to this representation,
• Within a particular representation, the symmetry adapted atomic orbitals mix more if their atomic energy level are closer.

Examples

H₂

H₂ 1sσ* antibonding molecular orbital

As a simple example consider the hydrogen molecule, H₂ (see molecular orbital diagram), with the two atoms labelled H' and H". The lowest-energy atomic orbitals, 1s' and 1s", do not transform according to the symmetries of the molecule. However, the following symmetry adapted atomic orbitals do:

1s' - 1s"	Antisymmetric combination: negated by reflection, unchanged by other operations
1s' + 1s"	Symmetric combination: unchanged by all symmetry operations

The symmetric combination (called a bonding orbital) is lower in energy than the basis orbitals, and the antisymmetric combination (called an antibonding orbital) is higher. Because the H₂ molecule has two electrons, they can both go in the bonding orbital, making the system lower in energy (and hence more stable) than two free hydrogen atoms. This is called a covalent bond. The bond order is equal to the number of bonding electrons minus the number of antibonding electrons, divided by 2. In this example there are 2 electrons in the bonding orbital and none in the antibonding orbital; the bond order is 1, and there is a single bond between the two hydrogen atoms.

He₂

On the other hand, consider the hypothetical molecule of He₂ (see molecular orbital diagram) with the atoms labelled He' and He". Again, the lowest-energy atomic orbitals, 1s' and 1s", do not transform according to the symmetries of the molecule, while the following symmetry adapted atomic orbitals do:

1s' - 1s"	Antisymmetric combination: negated by reflection, unchanged by other operations
1s' + 1s"	Symmetric combination: unchanged by all symmetry operations

Similar to the molecule H₂, the symmetric combination (called a bonding orbital) is lower in energy than the basis orbitals, and the antisymmetric combination (called an antibonding orbital) is higher. However, in its neutral ground state, each Helium atom contains two electrons in its 1s orbital, combining for a total of four electrons. Two electrons fill the lower energy bonding orbital, while the remaining two fill the higher energy antibonding orbital. Thus, the resulting electron density around the molecule does not support the formation of a bond between the two atoms (called a sigma bond), and the molecule does therefore not exist. Another way of looking at it is that there are two bonding electrons and two antibonding electrons; therefore, the bond order is 0 and no bond exists.

Noble gases

Considering a hypothetical molecule of He₂, since the basis set of atomic orbitals is the same as in the case of H₂, we find that both the bonding and antibonding orbitals are filled, so there is no energy advantage to the pair. HeH would have a slight energy advantage, but not as much as H₂ + 2 He, so the molecule exists only a short while. In general, we find that atoms such as He that have completely full energy shells rarely bond with other atoms. Except for short-lived Van der Waals complexes, there are very few noble gas compounds known.

Ionic bonds

→詳細は「Ionic bond」を参照

When the energy difference between the atomic orbitals of two atoms is quite large, one atom's orbitals contribute almost entirely to the bonding orbitals, and the other's almost entirely to the antibonding orbitals. Thus, the situation is effectively that some electrons have been transferred from one atom to the other. This is called an (mostly) ionic bond.

MO diagrams

→詳細は「Molecular orbital diagram」を参照

For more complicated molecules, the wave mechanics approach loses utility in a qualitative understanding of bonding (although is still necessary for a quantitative approach). The qualitative approach of MO uses a molecular orbital diagram. In this type of diagram, the molecular orbitals are represented by horizontal lines; the higher a line, the higher the energy of the orbital, and degenerate orbitals are placed on the same level with a space between them. Then, the electrons to be placed in the molecular orbitals are slotted in one by one, keeping in mind the Pauli exclusion principle and Hund's rule of maximum multiplicity (only 2 electrons, having opposite spins, per orbital; have as many unpaired electrons on one energy level as possible before starting to pair them).

HOMO and LUMO

→詳細は「HOMO/LUMO」を参照

The highest occupied molecular orbital and lowest unoccupied molecular orbital are often referred to as the HOMO and LUMO, respectively. The difference of the energies of the HOMO and LUMO, termed the band gap, can sometimes serve as a measure of the excitability of the molecule: the smaller the energy, the more easily it will be excited.

More quantitative approach

To obtain quantitative values for the molecular energy levels, one needs to have molecular orbitals which are such that the configuration interaction (CI) expansion converges fast towards the full CI limit. The most common method to obtain such functions is the Hartree-Fock method which expresses the molecular orbitals as eigenfunctions of the Fock operator. One usually solves this problem by expanding the molecular orbitals as linear combinations of gaussian functions centered on the atomic nuclei (see linear combination of atomic orbitals and basis set (chemistry)). The equation for the coefficients of these linear combinations is a generalized eigenvalue equation known as the Roothaan equations which are in fact a particular representation of the Hartree-Fock equation.

Simple accounts often suggest that experimental molecular orbital energies can be obtained by the methods of ultra-violet photoelectron spectroscopy for valence orbitals and X-ray photoelectron spectroscopy for core orbitals. This however is incorrect as these experiments measure the ionization energy, the difference in energy between the molecule and one of the ions resulting from the removal of one electron. Ionization energies are linked approximately to orbital energies by Koopmans' theorem. While the agreement between these two values can be close for some molecules, it can be very poor in other cases.

External links

• UC Berkeley video lecture on molecular orbitals
• Visualizations of some atomic and molecular orbitals (Note: These visualisations run only on Apple Mac.)
• Java molecular orbital viewer shows orbitals of hydrogen molecular ion.
• The orbitron, a visualization of all atomic, and some molecular and hybrid orbitals
• xeo Visualizations of some atomic and molecular atoms
• Simulations of molecules with electrons caught in molecular orbital (Simulations run on PC only.)

物理的意味

分子軌道が規格化されているならば、その絶対値の二乗に微小体積$d\mathbf {r}$を掛けたもの

$\phi _{i}^{*}(\mathbf {r} )\phi _{i}(\mathbf {r} )\,d\mathbf {r} =|\phi _{i}(\mathbf {r} )|^{2}\,d\mathbf {r}$

は、その微小体積$d\mathbf {r}$中に電子を見出す確率を表す。

応用

化学反応の理論的予測とその解釈。→フロンティア軌道理論

関連項目

• 分子軌道法
• 原子軌道