利用者:青子守歌/ワークスペース3

置換多面体（ちかんためんたい、フランス語: permutoèdre、英語: permutohedron）とは、超多面体の1種。特に $n$ 次置換多面体とは、以下のような $n -1$ 次元（超）多面体が $n$ 次元空間に埋め込まれた超多面体を指す。

頂点: 1から $n$ までの自然数の置換と対応している
辺: 値の差が1である2つの元だけが入れ替わっている（つまり、互換な）置換を座標を持つ頂点間を最短で張る

歴史

Günter M. Ziegler (1995)によると、置換多面体を最初に研究したのはPieter Hendrik Schoute (1911)である。この多面体にpermutoèdreと名付けたのはGeorges Th. Guilbaud and Pierre Rosenstiehl (1963)である。この名付けについて著者らは、読者への反論として「粗野ではあるが覚えやすい」^[1]と回答している。

英語ではpermutahedronと綴ることもある^[2]。またpermutation polytopesと呼ばれることもあるが、この表記はもっぱらバーコフ多面体（英語: Birkhoff polytope）において置換行列の凸包として定義される場合に用いられる。広義には、ある集合の置換と全単射な頂点を持つ任意の超多面体のことを指すこともあるV. Joseph Bowman (1972)。

頂点と辺と面

頂点, 辺, ファセット, 面
面の次元：

d = n - k

.

   k = 1    2    3    4    5
n
1      1                               1
2      1    2                          3
3      1    6    6                    13
4      1   14   36   24               75
5      1   30  150  240  120         541

$n$ 次の置換多面体において、頂点は $n!$ 個存在し、 $n - 1$ 個との点と接続されている。

また、辺は $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}(n − 1) n!/2$ 個存在し、その長さは $\sqrt 2$ である。辺が接続するのは、値が1異なる2つの座標軸の値を入れ替えた2点であり^[3]、この時入れ替えた座標軸が、辺の方向となる。

ファセットは $2 n - 2$ 個存在する（ ${1 \dots n}$ の空でない真部分集合 $S$ と対応するため）。部分集合 $S$ に対応するファセットの頂点は共通しており、その頂点の $S$ における座標は、 $S$ 以外に対応するファセットの頂点座標より小さい^[4]。

より一般的に言えば、0次元面（頂点）から $n - 1$ 次元面（置換多面体そのもの）までが、集合 ${1 \dots n}$ の狭義弱順序（英語: strict weak ordering）となる。よって、全ての面の数は、 $n$ 番目の順序ベル数（英語: ordered Bell number）となる^[5]。また、次元 $d$ の面は、 $k = n - d$ の同値類の順序と一致する。

$n$ 次の置換多面体にある $d = n - k$ 次元の面は、三角形 $T$ （オンライン整数列大辞典の数列 A019538）となり、

$T(n,k)=k!\cdot \left\{{n \atop k}\right\}$

である。ここに、 $\textstyle \left\{{n \atop k}\right\}$ は第2種スターリング数である。この値の例を、右の表に、行の合計値と順序ベル数とともに示す。

ファセットの例
3次		4次
3次の場合ファセットは6辺のことで、4次の場合は14面である。下図において $i \in S$ となる $i$ 番目の座標軸は暗灰色で示されている。この座標軸に対応する座標値は、残りの座標値より必ず小さくなっていることが分かる（例えば、4次の2要素部分集合の場合、灰色の座標軸にある値は必ず1,2であり残りの3,4より小さい値である）。
1要素部分集合	2要素部分集合	1要素部分集合	2要素部分集合	3要素部分集合

面の例

3次

4次

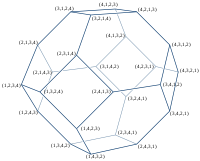
上記の画像は、3次および4次置換多面体の面格子（英語: face lattice）を図示したものである（空でない面のみ）。各面の中心点は狭義弱順序を示す（例えば、4次において面の中心に3 4 | 1 2と描かれている場合、それは $({3, 4}, {1, 2})$ の意味）。その順序は分割細分（英語: partition refinement）によって半順序となっており、細かい分割が外側になっている。面格子上の辺（置換多面体上ではないことに注意）に沿って進行すると、2つの隣接した同値類を統合することと等価となる。

頂点に示されるa | b | c | dは、順列(a, b, c, d)を表し、ケイリーグラフを構成する。

面間のファセット
先の例で示したファセットは、これらの面の中に存在し、2つの同値類の順序に対応する。 1つ目の同値類は、ファセットに割り当てられた部分集合 $S$ として用いられ、つまり順序は $(S, S c)$ となる。以下の画像は、 $n$ 次の置換多面体のファセットが、どのように $n$ 次の超立方体に)的射影されるかを表す。各点の縦棒は、2進表記された座標値を表し、部分集合 $S$ に対応する（例えば、0011は ${3, 4}$ の意味）。中心に射影された頂点はファセットではなく、射影の一部でない $n$ 次元超立方体の反対にある頂点もファセットではないことに注意。

Other properties

The permutohedron is vertex-transitive: the symmetric group S_n acts on the permutohedron by permutation of coordinates.

The permutohedron is a zonotope; a translated copy of the permutohedron can be generated as the Minkowski sum of the n(n − 1)/2 line segments that connect the pairs of the standard basis vectors .^[6]

The vertices and edges of the permutohedron are isomorphic to one of the Cayley graphs of the symmetric group, namely the one generated by the transpositions that swap consecutive elements. The vertices of the Cayley graph are the inverse permutations of those in the permutohedron.^[7] The image on the right shows the Cayley graph of S4. Its edge colors represent the 3 generating transpositions: (1, 2), (2, 3), (3, 4)

This Cayley graph is Hamiltonian; a Hamiltonian cycle may be found by the Steinhaus–Johnson–Trotter algorithm.

Tessellation of the space

Tesselation of space by permutohedra of orders 3 and 4

The permutohedron of order n lies entirely in the (n − 1)-dimensional hyperplane consisting of all points whose coordinates sum to the number

1 + 2 + … + n = n(n + 1)/2.

Moreover, this hyperplane can be tiled by infinitely many translated copies of the permutohedron. Each of them differs from the basic permutohedron by an element of a certain (n − 1)-dimensional lattice, which consists of the n-tuples of integers that sum to zero and whose residues (modulo n) are all equal:

x₁ + x₂ + … + x_n = 0, x₁ ≡ x₂ ≡ … ≡ x_n (mod n).

This is the lattice $A_{n-1}^{*}$ , the dual lattice of the root lattice $A_{n-1}$ . In other words, the permutohedron is the Voronoi cell for $A_{n-1}^{*}$ . Accordingly, this lattice is sometimes called the permutohedral lattice.^[8]

Thus, the permutohedron of order 4 shown above tiles the 3-dimensional space by translation. Here the 3-dimensional space is the affine subspace of the 4-dimensional space R⁴ with coordinates x, y, z, w that consists of the 4-tuples of real numbers whose sum is 10,

x + y + z + w = 10.

One easily checks that for each of the following four vectors,

(1,1,1,−3), (1,1,−3,1), (1,−3,1,1) and (−3,1,1,1),

the sum of the coordinates is zero and all coordinates are congruent to 1 (mod 4). Any three of these vectors generate the translation lattice.

The tessellations formed in this way from the order-2, order-3, and order-4 permutohedra, respectively, are the apeirogon, the regular hexagonal tiling, and the bitruncated cubic honeycomb. The dual tessellations contain all simplex facets, although they are not regular polytopes beyond order-3.

Examples

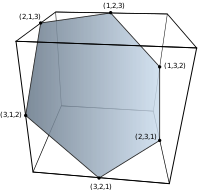
Order 2	Order 3	Order 4	Order 5	Order 6
2 vertices	6 vertices	24 vertices	120 vertices	720 vertices

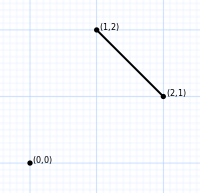
line segment	hexagon	truncated octahedron	omnitruncated 5-cell	omnitruncated 5-simplex

Notes

^ 原文（フランス語）："le mot permutoèdre est barbare, mais il est facile à retenir; soumettons-le aux critiques des lecteurs."
^ Thomas (2006)
^ Gaiha & Gupta (1977)
^ Lancia (2018), p. 105（The Permutahedronの章）.
^ See, e.g., Ziegler (1995), p. 18.
^ Ziegler (1995), p. 200.
^ This Cayley graph labeling is shown, e.g., by Ziegler (1995).
^ Baek, Jongmin; Adams, Andrew (2009). “Some Useful Properties of the Permutohedral Lattice for Gaussian Filtering”. Tech. Rep. (Stanford University).

References

Bowman, V. Joseph (1972), “Permutation polyhedra”, SIAM Journal on Applied Mathematics 22 (4): 580–589, doi:10.1137/0122054, JSTOR 2099695, MR 0305800, https://jstor.org/stable/2099695 .
Gaiha, Prabha; Gupta, S. K. (1977), “Adjacent vertices on a permutohedron”, SIAM Journal on Applied Mathematics 32 (2): 323–327, doi:10.1137/0132025, JSTOR 2100417, MR0427102, https://jstor.org/stable/2100417 .
Guilbaud, Georges Th.; Rosenstiehl, Pierre (1963), “Analyse algébrique d'un scrutin”, Mathématiques et Sciences Humaines 4: 9–33 .
Lancia, Giuseppe (2018), Compact extended linear programming models, Cham, Switzerland: Springer, ISBN 978-3-319-63975-8 .
Schoute, Pieter Hendrik (1911), “Analytic treatment of the polytopes regularly derived from the regular polytopes”, Verhandelingen der Koninklijke Akademie van Wetenschappen Te Amsterdam 11 (3): 87 pp Googlebook, 370–381 Also online on the KNAW Digital Library at http://www.dwc.knaw.nl/toegangen/digital-library-knaw/?pagetype=publDetail&pId=PU00011495
Thomas, Rekha R. (2006), “Chapter 9. The Permutahedron”, Lectures in Geometric Combinatorics, Student Mathematical Library: IAS/Park City Mathematical Subseries, 33, American Mathematical Society, pp. 85–92, ISBN 978-0-8218-4140-2 .
Ziegler, Günter M. (1995), Lectures on Polytopes, Springer-Verlag, Graduate Texts in Mathematics 152 .

External links

Bryan Jacobs. "Permutohedron". mathworld.wolfram.com (英語).
Alexander Postnikov (2005). "Permutohedra, associahedra, and beyond". arXiv:math.CO/0507163。

[1] 原文（フランス語）："le mot permutoèdre est barbare, mais il est facile à retenir; soumettons-le aux critiques des lecteurs."

[2] Thomas (2006)

[3] Gaiha & Gupta (1977)

[4] Lancia (2018), p. 105（The Permutahedronの章）.

[zface-5] See, e.g., Ziegler (1995), p. 18.

[6] Ziegler (1995), p. 200.

[7] This Cayley graph labeling is shown, e.g., by Ziegler (1995).

[8] Baek, Jongmin; Adams, Andrew (2009). “Some Useful Properties of the Permutohedral Lattice for Gaussian Filtering”. Tech. Rep. (Stanford University).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]