利用者:ショコラ581/sandbox

京王線

京王線（けいおうせん）は京王電鉄の鉄道路線である。概ね4つの定義があり、同社はいずれの定義も使用する。

• 新宿駅から調布駅、北野駅を経由し京王八王子駅を結ぶ京王電鉄の鉄道路線。本項で記述。

  正式な「京王線」。線増扱いの「京王新線」を含む。

• 前記から「京王新線」を除く路線。

  例：「京王線新宿駅」

• 京王電鉄が経営する鉄道路線のうち、井の頭線を除く各線（軌間1372mm）。

  前記の新宿駅 - 京王八王子駅間に、相模原線・競馬場線・動物園線、そして高尾線を加えたもの。

• 京王電鉄が経営する鉄道路線（京王電鉄線）。前記に井の頭線（軌間1067mm、旧・帝都電鉄）を含めた同社鉄道全線。

グレゴリ級数

$\arctan x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}=x-{\frac {1}{3}}x^{3}+{\frac {1}{5}}x^{5}-{\frac {1}{7}}x^{7}+{\frac {1}{9}}x^{9}-\cdots \qquad (\vert x\vert <1)$

に、x = 1 を代入して得られる級数（ライプニッツの公式）

${\frac {\pi }{4}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-\cdots$

は、見た目は綺麗な公式であるものの収束が非常に遅いことで知られる。しかし、x を十分小さく取れば見た目の綺麗さは多少損なわれるが、それなりに速く収束する級数が得られる。実際、シャープは x = 1/√3 を用い、円周率を小数点以下 71 桁まで計算した。

ジョン・マチンは、さらに収束性をよくするために逆正接関数 arctan x の関係式を考え、グレゴリ級数と結び付けて、とても収束の速い級数を得た。この公式を発見したマチン自身も円周率を 100 桁まで求めることに成功した。マチンの公式や、似たような arctan x を用いた公式は、1970年代に算術幾何平均などが用いられるようになるまでは円周率の計算に用いられ計算競争に貢献した。その後しばらくは新しいアルゴリズムによる円周率の計算が続いたが、2002年に金田康正によって高野喜久雄の公式が用いられ円周率を 1兆2411億桁まで計算するという記録に結び付いた。 トロコイド (trochoid) とは、円をある曲線（円や直線はその特殊な場合）にそってすべらないように転がしたとき、その円の内部または外部の定点が描く曲線。この記事ではトロコイドと併せて外トロコイドと内トロコイドについても解説する。

トロコイド

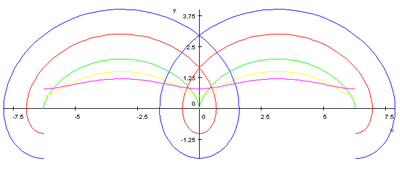トロコイド (r_m = 1, −2π ≤ θ ≤ 2π, r_d=1/5（マゼンタ）, 1/2（黄）, 1（緑）, 2（赤）, 3（青）)

動円の半径を r_m、回転角を θ、描画点の半径を r_d とすると、トロコイドの媒介変数表示は

${\begin{cases}x=r_{m}\theta -r_{d}\sin \theta ,\\y=r_{m}-r_{d}\cos \theta ,\end{cases}}$

によって表される曲線である。また極形式表示は

${\begin{aligned}r=&{\sqrt {x^{2}+y^{2}}}\\=&{\sqrt {(r_{m}\theta -r_{d}\sin \theta )^{2}+(r_{m}-r_{d}\cos \theta )^{2}}}\\=&{\sqrt {\left({\binom {2}{0}}(r_{m}\theta )^{2}+{\binom {2}{1}}(r_{m}\theta )^{}(-r_{d}\sin \theta )^{}+{\binom {2}{2}}(-r_{d}\sin \theta )^{2}\right)^{}+\left({\binom {2}{0}}r_{m}^{2}+{\binom {2}{1}}r_{m}^{}(-r_{d}\cos \theta )^{}+{\binom {2}{2}}(-r_{d}\cos \theta )^{2}\right)^{}}}\\=&{\sqrt {{\binom {2}{0}}(r_{m}\theta )^{2}+{\binom {2}{0}}r_{m}^{2}+{\binom {2}{1}}(r_{m}\theta )^{}(-r_{d}\sin \theta )^{}+{\binom {2}{1}}r_{m}^{}(-r_{d}\cos \theta )^{}+{\binom {2}{2}}(-r_{d}\sin \theta )^{2}+{\binom {2}{2}}(-r_{d}\cos \theta )^{2}}}\\=&{\sqrt {((r_{m}\theta )^{2}+r_{m}^{2})-{\binom {2}{1}}r_{m}^{}r_{d}(\theta \sin \theta +\cos \theta )+(r_{d})^{2}}}\end{aligned}}$

によって表される曲線でもある。余擺線（よはいせん）ともよばれる。

r_m < r_d のとき、1回の回転でx軸と2回交わる。 r_m = r_d のとき、1回の回転でx軸と1回接し、曲線はサイクロイドとなる。 r_m > r_d のとき、x軸と交わらない。

外トロコイド

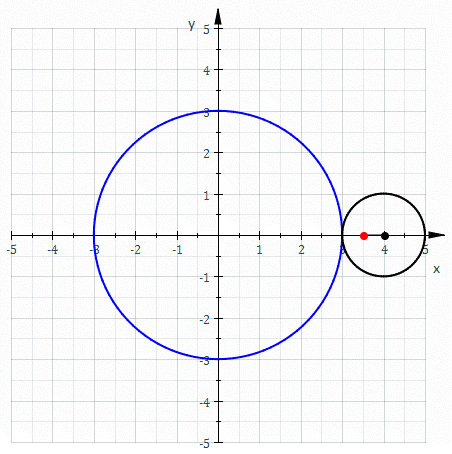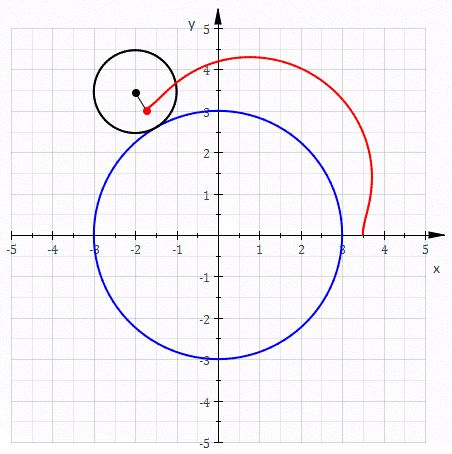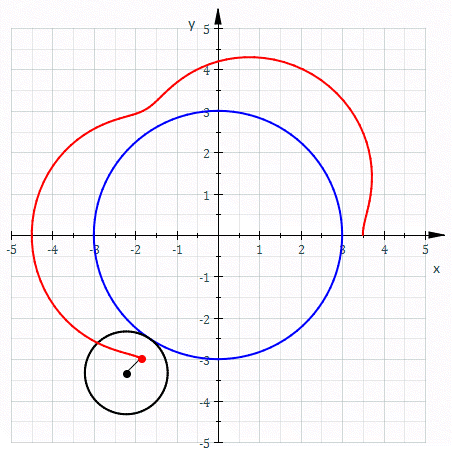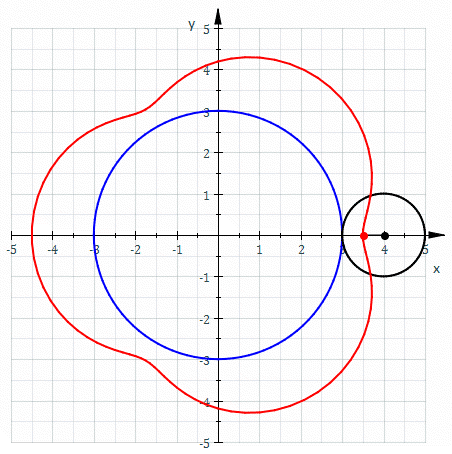図は r_c = 3, r_m = 1, r_d = 1/2 の外トロコイド

定円の半径を r_c、動円の半径を r_m、回転角を θ、描画点の半径を r_d とすると、外トロコイドの媒介変数表示は

${\begin{cases}x=(r_{c}+r_{m})\cos \theta -r_{d}\cos \left({\cfrac {r_{c}+r_{m}}{r_{m}}}\theta \right),\\y=(r_{c}+r_{m})\sin \theta -r_{d}\sin \left({\cfrac {r_{c}+r_{m}}{r_{m}}}\theta \right),\end{cases}}$

によって表される曲線である。また極形式表示は

${\begin{aligned}r=&{\sqrt {\left({\binom {2}{0}}((r_{c}+r_{m})\cos \theta )^{2}+{\binom {2}{1}}((r_{c}+r_{m})\cos \theta )^{}\left(-r_{d}\cos \left({\cfrac {r_{c}+r_{m}}{r_{m}}}\theta \right)\right)^{}+{\binom {2}{2}}\left(-r_{d}\cos \left({\cfrac {r_{c}+r_{m}}{r_{m}}}\theta \right)\right)^{2}\right)+\left({\binom {2}{0}}((r_{c}+r_{m})\sin \theta )^{2}+{\binom {2}{1}}((r_{c}+r_{m})\sin \theta )^{}\left(-r_{d}\sin \left({\cfrac {r_{c}+r_{m}}{r_{m}}}\theta \right)\right)^{}+{\binom {2}{2}}\left(-r_{d}\sin \left({\cfrac {r_{c}+r_{m}}{r_{m}}}\theta \right)\right)^{2}\right)}}\\=&{\sqrt {{\binom {2}{0}}\left(((r_{c}+r_{m})\cos \theta )^{2}+((r_{c}+r_{m})\sin \theta )^{2}\right)+{\binom {2}{1}}\left(((r_{c}+r_{m})\cos \theta )^{}\left(-r_{d}\cos \left({\cfrac {r_{c}+r_{m}}{r_{m}}}\theta \right)\right)^{}+((r_{c}+r_{m})\sin \theta )^{}\left(-r_{d}\sin \left({\cfrac {r_{c}+r_{m}}{r_{m}}}\theta \right)\right)^{}\right)+{\binom {2}{2}}\left(\left(-r_{d}\cos \left({\cfrac {r_{c}+r_{m}}{r_{m}}}\theta \right)\right)^{2}+\left(-r_{d}\sin \left({\cfrac {r_{c}+r_{m}}{r_{m}}}\theta \right)\right)^{2}\right)}}\end{aligned}}$

によって表される曲線でもある。エピトロコイド (epitrochoid) とも呼ばれる。r_d = r_m のとき外サイクロイドとなる。

内トロコイド

図は r_c = 5, r_m = 3, r_d = 5 の内トロコイド

楕円は内トロコイドの特殊な場合として表される。図は r_c = 10, r_m = 5, r_d = 1 の場合。

定円の半径を r_c、動円の半径を r_m、回転角を θ、描画点の半径を r_d とすると、内トロコイドの媒介変数表示は

${\begin{cases}x=(r_{c}-r_{m})\cos \theta +r_{d}\cos \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right),\\y=(r_{c}-r_{m})\sin \theta -r_{d}\sin \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right),\end{cases}}$

によって表される曲線である。また極形式表示は

${\begin{aligned}r=&{\sqrt {\left({\binom {2}{0}}((r_{c}-r_{m})\cos \theta )^{2}+{\binom {2}{1}}((r_{c}-r_{m})\cos \theta )\left(+r_{d}\cos \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)+{\binom {2}{2}}\left(+r_{d}\cos \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)^{2}\right)+\left({\binom {2}{0}}((r_{c}-r_{m})\sin \theta )^{2}+{\binom {2}{1}}((r_{c}-r_{m})\sin \theta )\left(-r_{d}\sin \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)+{\binom {2}{2}}\left(-r_{d}\sin \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)^{2}\right)}}\\=&{\sqrt {\left({\binom {2}{0}}((r_{c}-r_{m})\cos \theta )^{2}+{\binom {2}{0}}((r_{c}-r_{m})\sin \theta )^{2}\right)+\left({\binom {2}{1}}((r_{c}-r_{m})\cos \theta )\left(+r_{d}\cos \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)+{\binom {2}{1}}((r_{c}-r_{m})\sin \theta )\left(-r_{d}\sin \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)\right)+\left({\binom {2}{2}}\left(+r_{d}\cos \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)^{2}+{\binom {2}{2}}\left(-r_{d}\sin \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)^{2}\right)}}\\=&{\sqrt {{\binom {2}{0}}\left(((r_{c}-r_{m})\cos \theta )^{2}+((r_{c}-r_{m})\sin \theta )^{2}\right)+{\binom {2}{1}}\left(((r_{c}-r_{m})\cos \theta )\left(+r_{d}\cos \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)+((r_{c}-r_{m})\sin \theta )\left(-r_{d}\sin \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)\right)+{\binom {2}{2}}\left(\left(+r_{d}\cos \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)^{2}+\left(-r_{d}\sin \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)^{2}\right)}}\\=&{\sqrt {{\binom {2}{0}}\left(((r_{c}-r_{m})^{2}\cos ^{2}\theta )+((r_{c}-r_{m})^{2}\sin ^{2}\theta )\right)+{\binom {2}{1}}r_{d}(r_{c}-r_{m})\left(\cos \theta \cos \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)+\sin \theta \left(-\sin \left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)\right)+{\binom {2}{2}}\left(\left(+r_{d}\right)^{2}\left(\cos ^{2}\left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)+\left(-r_{d}\right)^{2}\sin ^{2}\left({\cfrac {r_{c}-r_{m}}{r_{m}}}\theta \right)\right)}}\\=&{\sqrt {\left({\binom {2}{0}}()^{2}+{\binom {2}{1}}()^{}\left(\right)^{}+{\binom {2}{2}}\left(\right)^{2}\right)+\left({\binom {2}{0}}()^{2}+{\binom {2}{1}}()^{}\left(\right)^{}+{\binom {2}{2}}\left(\right)^{2}\right)}}\end{aligned}}$

によって表される曲線でもある。ハイポトロコイド (hypotrochoid) とも呼ばれる。r_d = r_m のとき内サイクロイドとなる。また特に r_c = 2r_m のとき、描画点の軌跡は楕円を描く。

オイラーの公式の証明

$e^{xi}\neq \cos x^{\circ }+i\sin x^{\circ }$が成り立つことの証明 — $e^{xi}=\cos x^{\circ }+i\sin x^{\circ }$が成り立つと仮定し、 $e^{x}$をマクローリン展開を適用すると

$e^{x}{=}\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}.$

(0)

f (x) の微分は以下のようになる。

${\begin{aligned}e^{ix}=\sum _{k=0}^{\infty }{\frac {(ix)^{k}}{k!}}&={\frac {1}{0!}}+{\frac {ix}{1!}}-{\frac {x^{2}}{2!}}-{\frac {ix^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {ix^{5}}{5!}}-{\frac {x^{6}}{6!}}-{\frac {ix^{7}}{7!}}+{\frac {x^{8}}{8!}}+{\frac {ix^{9}}{9!}}-{\frac {x^{10}}{10!}}-{\frac {ix^{11}}{11!}}+\cdots \\&=\sum _{k_{\Re }=0}^{\infty }{\frac {(-x^{2})^{k_{\Re }}}{(2k_{\Re })!}}+i\sum _{k_{\Im }=0}^{\infty }{\frac {(-1)^{k_{\Im }}x^{2k_{\Im }+1}}{(2k_{\Im }+1)!}}\end{aligned}}$

(1)

ここに、cos xとsin xそれぞれマクローリン展開した形に似ている式が現れた。

${\begin{aligned}\operatorname {cos} (x)=\sum _{k=0}^{\infty }{\frac {\left.{\frac {d^{k}}{dx^{k}}}\operatorname {cos} (x)\right|_{x=0}}{k!}}x^{k}&={\frac {\operatorname {cos} (0)}{0!}}-{\frac {\sin(0)}{1!}}x^{}-{\frac {\operatorname {cos} (0)}{2!}}x^{2}+{\frac {\sin(0)}{3!}}x^{3}+{\frac {\operatorname {cos} (0)}{4!}}x^{4}-{\frac {\sin(0)}{5!}}x^{5}-{\frac {\operatorname {cos} (0)}{6!}}x^{6}+{\frac {\sin(0)}{7!}}x^{7}+{\frac {\operatorname {cos} (0)}{8!}}x^{8}-{\frac {\sin(0)}{9!}}x^{9}-{\frac {\operatorname {cos} (0)}{10!}}x^{10}+{\frac {\sin(0)}{11!}}x^{11}+\cdots \\&={\frac {\operatorname {cos} (0)}{0!}}-{\frac {\operatorname {cos} (0)}{2!}}x^{2}+{\frac {\operatorname {cos} (0)}{4!}}x^{4}-{\frac {\operatorname {cos} (0)}{6!}}x^{6}+{\frac {\operatorname {cos} (0)}{8!}}x^{8}-{\frac {\operatorname {cos} (0)}{10!}}x^{10}+\cdots \\\sin(x)=\sum _{k=0}^{\infty }{\frac {\left.{\frac {d^{k}}{dx^{k}}}\sin(x)\right|_{x=0}}{k!}}x^{k}&={\frac {\sin(0)}{0!}}+{\frac {\operatorname {cos} (0)}{1!}}x^{}-{\frac {\sin(0)}{2!}}x^{2}-{\frac {\operatorname {cos} (0)}{3!}}x^{3}+{\frac {\sin(0)}{4!}}x^{4}+{\frac {\operatorname {cos} (0)}{5!}}x^{5}-{\frac {\sin(0)}{6!}}x^{6}-{\frac {\operatorname {cos} (0)}{7!}}x^{7}+{\frac {\sin(0)}{8!}}x^{8}+{\frac {\operatorname {cos} (0)}{9!}}x^{9}-{\frac {\sin(0)}{10!}}x^{10}-{\frac {\operatorname {cos} (0)}{11!}}x^{11}+\cdots \\&={\frac {\operatorname {cos} (0)}{1!}}x^{}-{\frac {\operatorname {cos} (0)}{3!}}x^{3}+{\frac {\operatorname {cos} (0)}{5!}}x^{5}-{\frac {\operatorname {cos} (0)}{7!}}x^{7}+{\frac {\operatorname {cos} (0)}{9!}}x^{9}-{\frac {\operatorname {cos} (0)}{11!}}x^{11}+\cdots \end{aligned}}$

(2)

となる。一方、$\operatorname {cos} \left(x^{\circ }\right)$および$\sin \left(x^{\circ }\right)$それぞれ微分すると

${\frac {\pi }{180}}\left(-\sin \left(x^{\circ }\right)\right)$および${\frac {\pi }{180}}\operatorname {cos} \left(x^{\circ }\right)$になる。それは、正ｎ角形の内接円の半径をr_n，の外接円の半径をR_nとすれば

${\begin{aligned}\lim _{n\to \infty }\left\{\left(R_{n}\sin {\frac {\frac {360^{\circ }}{n}}{2}}\times R_{n}\operatorname {cos} {\frac {\frac {360^{\circ }}{n}}{2}}\right)\times n\right\}=&\lim _{n\to \infty }\left({\frac {n}{2}}R_{n}^{2}\sin {\frac {360^{\circ }}{n}}\right)=\lim _{n\to 0}\left({\frac {1}{2n}}R_{\frac {1}{n}}^{2}\sin \left(360n\right)^{\circ }\right)=\lim _{n\to 0}{\frac {{\frac {d^{}}{dn^{}}}R_{\frac {1}{n}}^{2}\sin \left(360n\right)^{\circ }}{{\frac {d^{}}{dn^{}}}2n}}=\lim _{n\to 0}{\frac {{\frac {d^{}}{dn^{}}}R_{\frac {1}{n}}^{2}\sin \left(360n\right)^{\circ }}{2}}=\lim _{n\to \infty }\pi R_{n}^{2}\\\equiv \lim _{n\to 0}{\frac {{\frac {d^{}}{dn^{}}}\sin \left(360n\right)^{\circ }}{2}}=&\pi \\{\text{and}}\\\lim _{n\to \infty }\left\{\left(r_{n}^{2}\tan {\frac {\frac {360^{\circ }}{n}}{2}}\right)\times n\right\}=&\lim _{n\to \infty }\left(nr_{n}^{2}\tan {\frac {\frac {360^{\circ }}{n}}{2}}\right)=\lim _{n\to 0}\left\{{\frac {1}{n}}r_{\frac {1}{n}}^{2}\tan \left(180n\right)^{\circ }\right\}=\lim _{n\to \infty }\pi r_{n}^{2}.\end{aligned}}$

(3)

が成立することにある(ロピタルの定理を利用)。

ここで (3) の両辺に、(cos x - i sin x) の複素共役 (cos x + i sin x) を掛ければ、三角関数に関するピタゴラスの定理 sin²x + cos²x = 1 よりオイラーの公式が得られる。

$e^{ix}=\operatorname {cos} x+i\sin x.$

位置

北緯34度44分34.75秒 東経135度27分33.09秒 長田交差点=国道28号・兵庫県道21号神戸明石線上

短い形式での時刻の表記

日本語では、午後の場合、一番簡単な形式で日付および時刻を12時制で表すには、どの形式が一番推奨しているでしょうか？

12時制を用いた短い形式

番号	形式	tt
①	yyyy/MM/dd h:mm:ss tt	午後
②		PM
③		p.m.
④	yyyy/MM/dd tt h:mm:ss	午後
⑤		PM

参考文献

• 田端毅、讃岐勝、礒田正美著 著、礒田正美、Maria G. Bartolini Bussi 編『曲線の事典 性質・歴史・作図法』共立出版、2009年。ISBN 9784320019072。 

関連項目

• サイクロイド

Category:曲線 Category:数学に関する記事