利用者:ぼのたけ/作業中

普遍性を翻訳中 from en:universal_property

数学の様々な分野において、ある特定の状況下にて一意にモルフィズム（morphism）を定めるような抽象的性質が、特定の構成を定義、あるいは特徴づけたりする事がしばしばある。このような性質を普遍性（universal property）と呼ぶ。普遍性は圏論を用いて抽象的に論考される。

結果として、我々は普遍性の一般的な扱い方を得ることになろう。いくつかの例を最初に学ぶ方が賢明である。例えば、群の直積や直和、自由群、積位相, ストーン－チェックのコンパクト化, テンソル積, 逆極限と順極限, 核と余核, 引き戻し, 押し出しおよびイコライザ、など。

形式的定義

U : D → C を圏 D から圏 C への関手とし、X をCの対象とする。X から Uへの普遍射 （universal morphism）は、D の対象 A とCのモルフィズム φ : X → U(A) からなる対 (A, φ)で表され、かつ以下の普遍性（universal property）を満たす。

Y がDの対象で f : X → U(Y) がCのモルフィズムであるような場合、常にモルフィズム g : A → Yが一意に存在して、次の図を可換にする。

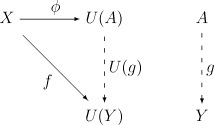
モルフィズム g の存在は、直感的にはA が「十分に一般的」であることを示しながら、一方でモルフィズムの一意性は、 A が「十分に一般的ではない」事を表している。

また、上述の定義で全ての射を逆向きにすることで、圏論的な双対を考えることができる。U から X への普遍射は、Dの対象A とCのモルフィズム φ : U(A) → X の対 (A, φ) で表され、かつ以下の普遍性を満たす。

Y が Dの対象で f : U(Y) → X がCのモルフィズムであるような場合、常にモルフィズムg : Y → A が一意に存在して、次の図を可換にする。

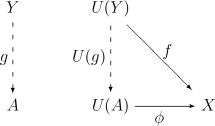
ここで、人によっては一方を普遍射と呼び、もう一方を余普遍射（co-universal property）と呼ぶ場合もある事に注意されたい。どちらがどちらかはその人次第である。

さまざまな普遍性

存在と一意性

数量を定義することがその存在を保障することにはならない。与えられた関手U及び上述の対象Xに対し、X から U （もしくはU から X）の普遍射は、存在するかもしれないし、存在しないかもしれない。しかしながら、もし、普遍射 (A, φ) が存在すれば、一意な同型射を除いて一意に定まる。すなわち、もし別の対 (A′, φ′) が存在すれば、一意な同型射g : A → A′ が存在して φ′ = U(g)φ となる。これは (A′, φ′) を普遍者の定義にしたがって (Y, f) と置き換えることで容易に確かめられる。

同値な定義

普遍射の定義は様々な方法で置き換えることができる。U を D から C への関手とし、X を C の対象とする。このとき、以下は全て同値である。

(A, φ) は X から U への普遍射である
(A, φ) はコンマ圏 (X ↓ U) の始対象である
(A, φ) は Hom_C(X, U—) の表現である。

これらと双対な以下の定義もまたぞれぞれに同値である。

(A, φ) は U から X への普遍射である。
(A, φ) はコンマ圏 (U ↓ X) の終対象である。
(A, φ) は Hom_C(U—, X) の表現である。

随伴関手との関係

Suppose (A₁, φ₁) is a universal morphism from X₁ to U and (A₂, φ₂) is a universal morphism from X₂ to U. By the universal property, given any morphism h : X₁ → X₂ there exists a unique morphism g : A₁ → A₂ such that the following diagram commutes:

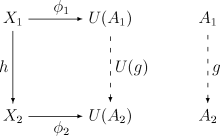
If every object X_i of C admits a universal morphism to U, then the assignment X_i $\mapsto$ A_i and h $\mapsto$ g defines a functor V from C to D. The maps φ_i then define a 自然変換 from 1_C (the identity functor on C) to U V. The functors (V, U) are then a pair of 随伴関手s, with V left-adjoint to U and U right-adjoint to V.

Similar statements apply to the dual situation of morphisms from U. If such morphisms exist for every X in C one obtains a functor V : C → D which is right-adjoint to U (so U is left-adjoint to V).

Indeed, all pairs of adjoint functors arise from universal constructions in this manner. Let F and G be a pair of adjoint functors with unit η and co-unit ε (see the article on 随伴関手 for the definitions). Then we have a universal morphism for each object in C and D:

For each object X in C, (F(X), η_X) is a universal morphism from X to G. That is, for all f : X → G(Y) there exists a unique g : F(X) → Y for which the following diagrams commute.
For each object Y in D, (G(Y), ε_Y) is a universal morphism from F to Y. That is, for all g : F(X) → Y there exists a unique f : X → G(Y) for which the following diagrams commute.

Universal constructions are more general than adjoint functor pairs: a universal construction is like an optimization problem; it gives rise to an adjoint pair if and only if this problem has a solution for every object of C (equivalently, every object of D).

例

We give a few worked examples to highlight the general idea. The reader can construct numerous other examples by consulting the articles mentioned in the introduction.

テンソル代数

Let C be the ベクトル空間の圏 K-Vect over a 体 K and let D be the category of algebras K-Alg over K (assumed to be unital and associative). Let U be the 忘却関手 which assigns to each algebra its underlying vector space.

Given any ベクトル空間 V over K we can construct the テンソル代数 T(V) of V. The universal property of the tensor algebra expresses the fact that the pair (T(V), i), where i : V → T(V) is the inclusion map, is a universal morphism from V to U.

Since this construction works for any vector space V, we conclude that T is a functor from K-Vect to K-Alg. This functor is left-adjoint to the forgetful functor U.

核

Suppose D is a category with ゼロモルフィズムs (such as the 群の圏) and f : X → Y is a morphism in D. A 核 of f is any morphism k: K → X such that

f k is the zero morphism from K to Y;
Given any morphism k′: K′ → X such that f k′ is the zero morphism, there is a unique morphism u: K′ → K such that k u = k′.

To understand this in the framework of the general setting above, we define the category C of morphisms in D. The objects of C are morphisms f : X → Y in D, and a morphism from f : X → Y to g : S → T is given by a pair (α,β) of morphisms α : X → S and β : Y → T such that βf = gα.

Define a functor F : D → C that maps an object K of D to the zero morphism 0_KK : K → K and a morphism r : K → L to the pair (r,r).

Now, given a morphism f : X → Y in the category D (thought of as an object in the category C) and an object K of D, a morphism from F(K) to f is given by a pair (k,l) such that f k = l 0_KK = 0_KY, which is exactly what shows up in the universal property of kernels given above. The abstract “universal morphism from F to f ” is nothing but the universal property of a kernel.

極限と余極限

極限と余極限 are important special cases of universal constructions. Let J and C be categories with J 小さい (J is thought of as an 添字圏) and let C^J be the corresponding 関手圏（functor category）. The diagonal functor Δ : C → C^J is the functor that maps each object N in C to the constant functor Δ(N) : J → C to N (i.e. Δ(N)(X) = N for each X in J).

Given a functor F : J → C (thought of as an object in C^J), the limit of F, if it exists, is nothing but a universal morphism from Δ to F. Dually, the colimit of F is a universal morphism from F to Δ.

どのようなメリットがあるのか

Once one recognizes a certain construction as given by a universal property, one gains several benefits:

Universal properties define objects up to a unique isomorphism; one strategy to prove that two objects are isomorphic is therefore to show that they satisfy the same universal property.
The concrete details of a given construction may be messy, but if the construction satisfies a universal property, one can forget all those details: all there is to know about the construct is already contained in the universal property. Proofs often become short and elegant if the universal property is used rather than the concrete details.
If the universal construction can be carried out for every X in C, then we know that we obtain a 関手 from C to D. (So for example, forming kernels is functorial: every morphism (α,β) from the morphism f to the morphism g induces a morphism from the kernel of f to the kernel of g.)
Furthermore, this functor is a right or left adjoint to U. But right adjoints commute with 極限 and left adjoints commute with 余極限! (So we can for example immediately conclude that the kernel of a 直積 of maps is equal to the product of the kernels.)

歴史

様々な位相幾何学的構成における普遍性は1948年にピエール・サミュエルによって示された。これらは後にブルバキにて拡張された形で用いられた。随伴関手に近い関係を持つ概念はそれ自体独立した形で、1958年にダニエル・カンによって導入された。

参考文献

Cohen, Paul M., Universal Algebra (1981), D.Reidel Publishing, Holland. ISBN 90-277-1213-1.
Mac Lane, Saunders, Categories for the Working Mathematician 2nd ed. (1998), Graduate Texts in Mathematics 5. Springer. ISBN 0-387-98403-8.