ロジカルエフォート

ロジカルエフォート（Logical effort）とは1991年にIvan SutherlandとBob Sproullによって造られた用語であり、CMOS回路の遅延を推定するための簡便な方法に用いられる概念である。

ロジカルエフォートによる考え方を適切に使用することで、特定の機能を持つ論理ゲートの選択と、最小遅延を実現するためのゲートのサイズやステージ数の設定に役立つ。

論理ゲートにおける遅延の導出

ゲートの遅延は基準となる遅延時間を単位として表現される。単位となる基準遅延としては、インバータがそれ自身と同一のインバータを駆動する際（この時配線やその他負荷による余剰な容量は付いていないものとする）の遅延、$\tau =3RC$ が用いられる。基準遅延に掛けられる無次元の係数は正規化遅延として知られる。（著者によっては、1つのインバータがそれと同一な4つのインバータを駆動する際の遅延時間である、ファンアウト4遅延を基準遅延として定義する場合もある。）実際の遅延時間は、ゲートの正規化遅延 $d$ と基準遅延 $\tau$ の積として下記のように簡単に定義される。

$d_{abs}=d\cdot \tau$

典型的な600 nmプロセスでは、基準遅延 $\tau$ は50 ps程度である。250 nmプロセスでは $\tau$ が20 ps程度、45 nmプロセスでは4～5 ps程度となる。

論理ゲートにおける正規化遅延は2つの主要項の和として表現することができる。つまり、正規化寄生遅延 $p$（これはゲートの内在的な遅延であり、無負荷を駆動する際の遅延として捉えられる）と、ステージエフォート $f$（これは下記で説明されるように容量負荷に依存する）を用いて以下のように表現される。

$d=f+p$

ステージエフォート $f$ はさらに2つの要素に分けられる。ロジカルエフォート $g$ は、与えられたゲートがインバータと同じ出力電流を持つ時の、インバータに対する入力容量の比である。（あるいは逆に、入力容量をインバータと揃えた時に、出力電流がどれだけ弱まり遅延が増大するかを捉えた量であるとも言える。）特定のゲートクラスは一定のロジカルエフォートの値を持ち、ゲートの内在的な性質を捉えていると説明される。 エレクトリカルエフォート $h$ は、与えられたゲートの入力容量と出力負荷の容量との比である。"ロジカルエフォート"は出力負荷に依存せず、出力負荷の大きさは"エレクトリカルエフォート"として考慮される。これら2つの要素を用いてステージエフォートは下式のように簡単に表される。

$f=gh$

上記の2式を組み合わせることで、単一の論理ゲートが持つ正規化遅延は次のような基本方程式としてモデル化される。

$d=gh+p$

単一ステージのロジカルエフォートを計算する手続き

クリティカルパスに沿ったCMOSインバータは、典型的にはガンマの値が2に等しくなるようにして設計される。言い換えればインバータのpMOSは、nMOSの2倍のゲート幅を持つように設計される。（このときpMOSのゲート容量はnMOSの2倍となる。）これはpMOSの抵抗値とnMOSの抵抗値をおおまかに揃えることで、同程度のプルアップ電流とプルダウン電流を得るためである。

すべてのトランジスタのサイズは出力の駆動能力がインバータの駆動能力と等しくなるように、サイズ2のpMOSとサイズ1のnMOSから構成されることになる。

ゲートの出力駆動能力は、可能な入力の全組み合わせの中で最小の出力駆動能力と等しくなる。

与えられた入力に対するゲートの出力駆動能力は、ゲートの出力ノードの駆動能力に等しい。

ノードの駆動能力は、そのノードにソースまたはドレインが接続されたON状態のすべてのトランジスタの駆動能力の和と等しい。PMOSトランジスタはゲート電圧が0であるときにON状態となる。NMOSトランジスタはゲート電圧が1であるときにON状態となる。

ゲートのサイズが決まれば、ゲートの出力のロジカルエフォートは出力ノードにソースまたはドレインが接続されたすべてのトランジスタのゲート幅の和となる。ゲートの各入力のロジカルエフォートは、その入力ノードに繋がったすべてのトランジスタのゲート幅の和となる。

ゲート全体のロジカルエフォートは、出力のロジカルエフォートと入力のロジカルエフォートの総和との比になる。

複数ステージの論理ネットワーク

ロジカルエフォートの大きな利点は、その考え方を複数ステージからなる回路に容易に拡張できることである。パスの正規化遅延の総和 $D$ は全体のパスエフォート $F$ とパスの寄生遅延 $P$（個別の寄生遅延の和）を用いて次のように書き表すことができる。

$D=NF^{1/N}+P$

パスエフォートはパスのロジカルエフォート $G$（個別のゲートのロジカルエフォートの積）とパスのエレクトリカルエフォート $H$（パスの入力容量と負荷との比）を用いて表すことができる。

各ゲートがそれぞれただ一つの追加のゲート（つまりパスの次のゲート）を駆動する場合、パスエフォートは下記のように表される。

$F=GH$

回路が分岐を持つ場合、追加の分岐エフォート $b$ を考慮に入れる必要が出てくる。それはゲートによって駆動される総容量と、着目するパスの容量との比である。

$b={\frac {C_{onpath}+C_{offpath}}{C_{onpath}}}$

パスの分岐エフォート $B$ は各ステージの分岐エフォートの積として与えられる。 すなわち全体のパスエフォートは下式で表される。

$F=GHB$

ゲートが追加のただ一つのゲートを駆動する場合は $b=1$ となり、それらの積は $B=1$ で固定されるため、分岐がない場合の表式と一致することが分かる。

最小遅延

複数ステージからなる論理ネットワークにおいて、特定のパスに沿った実現可能な最小の遅延は、各ステージのエフォートが等しくなるように設計したときに達成されることが示される。ゲートの組み合わせが与えられ、負荷の大きさが分かれば、$B,G,H$ の値が定まり $F$ が固定される。 それゆえ個別のゲートは、各ステージのエフォートが下式となるようにサイズが決定される。

$f=F^{1/N}$

ここで $N$ は回路中のステージ数である。

具体例

インバータの遅延

CMOSインバータ回路

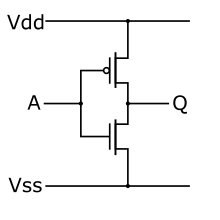
定義からインバータのロジカルエフォート $g$ は1である。インバータが同一のインバータを駆動する場合、エレクトリカルエフォート $h$ も1となる。

インバータの寄生遅延 $p$ もまた1である。(これはインバータのエルモア遅延モデルを考えることで求められる。)

以上から、インバータがそれと同一のインバータを駆動する際の正規化遅延は下式のように求められる。

$d=gh+p=(1)(1)+1=2$

NANDとNORゲートの遅延

2入力NANDゲートのロジカルエフォートは $g=4/3$ と計算される。なぜなら入力容量が3のインバータと同等の電流を駆動するために、NANDゲートは4の入力容量を必要とするためである。同様に2入力NORゲートのロジカルエフォートは $g=5/3$ となることが分かる。ロジカルエフォートが小さいため、典型的にはNORゲートよりもNANDゲートの方が好まれる。

さらに大きなゲートに対しては、ロジカルエフォートは下表のようになる。

各入力数の静的CMOSゲートのロジカルエフォート（ガンマの値 = 2）

	入力数
ゲートの種類	1	2	3	4	5	n
インバータ	1	N/A	N/A	N/A	N/A	N/A
NAND	N/A	${\frac {4}{3}}$	${\frac {5}{3}}$	${\frac {6}{3}}$	${\frac {7}{3}}$	${\frac {n+2}{3}}$
NOR	N/A	${\frac {5}{3}}$	${\frac {7}{3}}$	${\frac {9}{3}}$	${\frac {11}{3}}$	${\frac {2n+1}{3}}$

NANDとNORゲートの正規化寄生遅延はそれぞれの入力数と等しくなる。

以上から、2入力NANDがそれ自体と同一のコピーを駆動する際（エレクトリカルエフォートが1のとき）の遅延は下記のようになる。

$d=gh+p=(4/3)(1)+2=10/3$

2入力のNORゲートの遅延は下記のようになる。

$d=gh+p=(5/3)(1)+2=11/3$

参考文献

• Sutherland, Ivan E.; Sproull, Robert F.; Harris, David F. (1999). Logical Effort: Designing Fast CMOS Circuits. Morgan Kaufmann. ISBN 1-55860-557-6. https://books.google.com/books?id=hGVWzQmQYP0C&pg=PP1&dq=logical+effort+cmos 
• Weste, Neil H. E.; Harris, David (2011). CMOS VLSI Design: A Circuits and Systems Perspective, 3rd Ed.. Pearson/Addison-Wesley. ISBN 0-321-54774-8. https://books.google.com/books?id=ACxTAAAAMAAJ&q=cmos+vlsi+design&dq=cmos+vlsi+design