ミニマックス法
ミニマックス法(ミニマックスほう、英: minimax)またはミニマックス探索とは、想定される最大の損害が最小になるように決断を行う戦略のこと。将棋、チェス、リバーシなどといった二人零和有限確定完全情報ゲームをコンピュータに思考させるためのアルゴリズムとしても用いられるが、元々はフォン・ノイマンが中心となって数学的に理論化されたゲーム理論において、打ち手を決定する際に適用されるルールの一つ。[1] これに対し、想定される最小の利益が最大になるように決断を行う戦略はマクシミン戦略という。
ゲーム木
[編集]完全情報ゲームは、お互いがどの手を打ったかによってどのような局面が出現するかを場合分けしていくことでゲーム展開を樹形図にできる。このように現在の局面から出現するすべての局面の関係をゲーム木と呼ぶ。
ゲーム木は各段階で枝分かれてしていくが、枝分かれの数はプレーヤーの選択肢の数だけあり、ゲーム木を下にたどる(より先を読む)につれ局面(節点)の数は劇的に増加する。
思考プログラムの基本的な考え方
[編集]思考プログラムの基本は、局面がどの程度自分にとって有利か点数を付ける(評価する)ことである。局面の有利度を適切に評価することができれば、自分の打てる手のうち、最も評価の高い局面を出現させるような手を選択すればよいことになる。
局面に置かれている駒の位置・数などだけから算出した評価値を静的評価値、算出する関数を静的評価関数と呼ぶ。「静的」とはここでは先読みをしていないことを意味する。通常、静的評価関数だけで適切な局面評価を行うことは困難である。そのため、先読みを実現するのがこのミニマックス法である。
先読み
[編集]先を読んだ上で、ある局面がどの程度有利であるかを評価するには、以下の考え方を用いればよい。
- 読みたい局面が相手の番であれば、その局面の次に出現するすべての局面のうち最も悪い(不利な)、つまり相手にとって最も有利な(評価値が最小)手を相手は打ってくるはずである。そこで、次に出現するすべての局面の評価値の最小値を局面の評価値にすればよい。
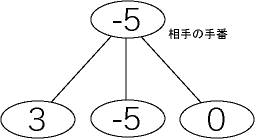
- 読みたい局面が自分の番であれば、その局面の次に出現するすべての局面のうち最も良い評価(評価値が最大)の手を打つことができる。そこで、次に出現するすべての局面の評価値の最大値を局面の評価値にすればよい。

相手番の局面の評価値を求めるには、次に出現するすべての局面(自分番)の評価値を求めればいいので、その自分番の評価値を求めるには・・・、と再帰的にゲーム木を展開していくことで求めることができる。
何手先まで読むかによって、その深さまで展開したところでは静的評価関数を用いることで探索を打ち切ることができる。前述したように、ゲーム木は深くなるにつれ局面数が爆発的に増える。そのため、ある程度以上の深さまで先読みをしようとすると、実用的な時間では難しくなってくる。
通常は有限の深さまで読むことで打ち切るが、ゲーム終了まで読めばゲームの勝敗を完全に読み切った上で、最善の手を打つことができる。終盤の読みや詰め将棋の解答などは完全読みが行われる(長手数の詰め将棋の解答では完全読みを行わないこともある)。リバーシのように勝敗だけでなく石差も問題となるゲームでは、勝敗のみを読み切ることを必勝読み、石差まで読み切ることを完全読みと区別する。
必勝読みでは、各局面の評価値は「勝ち」か「負け」の2通りに限定される。この場合、自分の手番の局面は、次の局面に「一つでも勝ち」があれば(自分はその局面を選択すればよいので)勝ちが決定し、相手の手番の局面は、次の局面が「すべて勝ち」なら(相手には負けを阻止する選択肢がないので)勝ちが決定する。これらは各局面の評価値の論理和(OR)、論理積(AND)とったものであることから、それぞれORノード、ANDノードと呼ばれる。このように評価値が勝敗のみで表されるゲーム木は、特にAND/OR木と呼ばれる。
擬似プログラム
[編集]以上のアルゴリズムを擬似コードで記述すると以下のようになる。
function MIN_MAX(position:局面, depth:integer): integer
begin
if depth=0 then return STATIC_VALUE(position); {読み深さに達した}
positionを展開→すべての子ノードをchildren[]に。子ノードの数をwに。
if w=0 then return STATIC_VALUE(position); {終局}
if positionは自分の局面 then begin
max := -∞;
for i:=1 to w do begin
score = MIN_MAX( children[i], depth-1);
if(score>max) max := score;
end;
return max;
end else begin{positionは相手の局面}
min := ∞;
for i:=1 to w do begin
score = MIN_MAX( children[i], depth-1);
if(score<min) min := score;
end;
return min;
end;
end;
ネガマックス法
[編集]チェスなどパスのないゲームでは、ノードごとに評価値の正負を逆転させることで「相手は自分にとって損な手を探索する」のではなく「相手は相手にとって得な手を探索する」ように書き換えることができる。これをネガマックス(Negamax)法と呼ぶ。
function NEGA_MAX(position:局面, depth:integer): integer
begin
if depth=0 then return STATIC_VALUE(position); {読み深さに達した}
positionを展開→すべての子ノードをchildren[]に。子ノードの数をwに。
if w=0 then return STATIC_VALUE(position); {終局}
max := -∞;
for i:=1 to w do begin
score = -NEGA_MAX( children[i], depth-1);
if(score>max) max := score;
end;
return max;
end;
応用アルゴリズム
[編集]ミニマックス法はすべての局面に対してしらみつぶしに探索を行うため、実際には読む必要のない(評価しなくても支障がない)手も読むことになり探索効率が悪い。これを改善したアルゴリズムとしてα-β法がある。α-β法は、読む必要のない手を打ち切ることで高速化を図っている。
実際のゲームプログラムではα-β法をさらに応用したアルゴリズムが用いられることが多い。
脚注
[編集]- ^ A Beautiful Math, Tom Siegfriend ISBN 978-4-16-765171-8




