コクセター群
この項目「コクセター群」は翻訳されたばかりのものです。不自然あるいは曖昧な表現などが含まれる可能性があり、このままでは読みづらいかもしれません。(原文:en:Coxeter group 03:41, 11 August 2011) 修正、加筆に協力し、現在の表現をより自然な表現にして下さる方を求めています。ノートページや履歴も参照してください。(2011年8月) |
数学においてコクセター群(コクセターぐん、英: Coxeter group)とは鏡映変換で表示できる抽象群のことである。ハロルド・スコット・マクドナルド・コクセターに因んで名づけられた。有限コクセター群は何らかのユークリッド鏡映群(たとえば一般次元正多胞体の対称変換群など)になっている。もちろん、すべてのコクセター群が有限群とは限らないし、すべてのコクセター群をユークリッド的な鏡映や対称変換として記述できるわけでもない。コクセター群は鏡映群の抽象化として導入され(Coxeter 1934)、有限コクセター群の分類は完了している(Coxeter 1935) 。
コクセター群は数学のいくつもの分野に現れる。一般次元正多胞体の対称変換群や単純リー代数のワイル群は有限コクセター群の例であり、ユークリッド平面や双曲平面の正則三角形分割 (regular tessellation) に対応する三角群や無限次元カッツ-ムーディ代数のワイル群は無限コクセター群の例である。
コクセター群に関する標準的な文献としては (Humphreys 1990) や (Davis 2007) などがある。
定義
[編集]生成系 S をもつ群 W がコクセター群である、または組 (W, S) がコクセター系 (Coxeter system) であるとは、以下の3条件がすべて満たされるときにいう。
- S は対合からなる: s ∈ S ならば、必ず s2 = 1 が成り立つ。
- 組み紐関係式 (braid relation): s, t ∈ S が s ≠ t であるならば、2 以上のある整数(または ∞)ms,t で (st)ms,t = 1 となるものが取れる。
- それ以外に生成元の間には関係がない。
ただし、ms,t = ∞ は s と t の間に関係がないことを表す。これは次のように書く事もできる。
- s ∈ S ならば s-1 = s が成り立つ。
- s, t ∈ S で s と t が相異なるとき、s と t には関係が無いか、関係がある場合には次が成り立つ; s と t を交互に ms,t 個並べる方法が 2 通りあるが、そのいずれも同じ元を定めるような 2 以上の整数 ms,t が存在する。
- stststst… = tstststs… (両辺とも因数の数は ms,t 個)
- 生成元はそれ以外に関係式を持たない。
また、S = {x1, x2, ..., xn} とすれば以下のように表示できる:
ただし、i, j, k = 1, 2, ..., n かつ mi,j (i ≠ j) は 2 以上の整数か ∞ である。
(W, S) がコクセター系であるとき、生成系 S に属する元の個数 |S| をコクセター群 W の階数 (rank) といい、rank W と表す。また生成元の部分集合 J ⊆ S で生成されるコクセター群 W の部分群 WJ もコクセター群になる。このような部分群 WJ を放物型部分群という。
G が S を生成系とするコクセター群であるとき、(st)ms,t = 1 となるms,t (s, t ∈ S) を成分とする |S| 次の対称行列
をコクセター行列 (Coxeter matrix) (あるいは行列要素 ms,t を 2 変数の関数と見て、コクセターデータ)という。ただし、s ∈ S に対して ms,s = 1 である。コクセター行列が与えられたとき、コクセター図形 (Coxeter graph, Coxeter diagram) と呼ばれる図形が
- 各生成元 s ∈ S に対応して、|S| 個の頂点を打つ。
- ms,t = 2 ならば何もしない。
- ms,t ≥ 3 ならば s, t に対応する頂点を辺で結び、辺に ms,t の値を記す。
という手順で定まる。逆に、コクセター図形が 1 つ与えられれば、コクセター行列を復元することができ、したがってコクセター群が一つ定められる。すなわち、コクセター群を与えること、コクセター行列を与えること、コクセター図形を与えることの三者は等価である。
コクセター図形が 2 つ以上の連結成分に分かれるとき、対応するコクセター群は各連結成分に対応するコクセター群たちの直積に分解される。連結なコクセター図形あるいはそれに対応するコクセター群は既約であるという。
例
[編集]Sn+1 を n + 1 次対称群とする。n 個の互換 si = (i, i + 1) (i = 1, 2, 3, ..., n) をとると Sn+1 は {s1, s2, ..., sn} を生成系とするコクセター群となる。
また二面体群もコクセター群である。
鏡映群との関係
[編集]コクセター群は鏡映群の概念と深く結びついている。単純に見ると、コクセター群が(生成元と基本関係によって与えられる)抽象群である一方、鏡映群は(線型代数群の部分群またはその適当な一般化として与えられる)具体群である。実際、コクセター群は鏡映群の研究の過程でその抽象化として生まれたものである。鏡映群は鏡映(つまり位数 2 の合同変換)で生成される線型代数群の部分群であり、他方のコクセター群は対合(つまり位数 2 の変換、鏡映の抽象化)で生成されるが、これらの間の対応はある決まった仕方で与えられる(基本関係 (rirj)k は π/k の角度で交わる超平面に対応しており、rirj の位数が k であるということが 2π/k の回転の抽象化になっている)。
鏡映群からこのようにして得られる抽象群はコクセター群であり、逆に鏡映群をコクセター群の線型表現とみなすことができる。有限コクセター群に対しては、この対応は(函手として)完全である。つまり、任意の有限コクセター群はある次元のユークリッド空間における有限鏡映群としての忠実な表現を持つ。一方、無限コクセター群は必ずしも鏡映群として表現されるとは限らない。
歴史的には (Coxeter 1934) で任意の鏡映群がコクセター群であること(すなわち任意の鏡映群に対して、基本関係が ri2 または (rirj)k で尽くされるような表示ができること)が示されており、実際この論文でコクセター群の概念が導入されている。逆に (Coxeter 1935) で有限コクセター群が必ず何らかの鏡映群として表現できることが示されており、したがってこれで有限コクセター群の分類は終了している。
有限コクセター群
[編集]
分類
[編集]有限コクセター群のコクセター-ディンキン図形を用いた分類が (Coxeter 1935) に述べられている。有限コクセター群は有限次元ユークリッド空間の鏡映群として表現される。
具体的には、有限コクセター群は階数をひとつのパラメータとする三つの無限族 An, BCn, Dn と二次元で一つのパラメータを持つ族 I2(p) がひとつ、さらに六つの例外群 E6, E7, E8, F4 H3, H4 のいずれかとなる。
ワイル群
[編集]有限コクセター群は全てではないにしろほとんどがワイル群であり、逆にすべてのワイル群はコクセター群として実現できる。ワイル群となるのは無限族 An, BCn, Dn の各群と例外群 E6, E7, E8, F4 および I2(6)(ワイル群の記法でいうところの G2)であり、ワイル群とならないのは例外群の H3, H4 および無限族 I2(p)(ただし、この中に別のワイル群と一致するものがあるが、それを除く。具体的には
が除外される)。
このことは、有限群の場合に限ってコクセター図形と(無向)ディンキン図形とを比較することによって示される。きちんと言えば、コクセター=ディンキン図形はディンキン図形から辺の向きを忘れて、二重辺は 4 でラベル付けられた辺に、三重辺は 6 でラベル付けられた辺に取り替えることによって得られる。もうひとつ留意点として、任意の有限生成コクセター群がオートマチック群 (Automatic group) であること[1]である。ディンキン図形には、辺のラベルとして 2, 3, 4, 6 しか付けられないという制限が追加されることになる。幾何的にはこれは結晶構造制限定理[訳語疑問点] (crystallographic restriction theorem) に対応しており、事実としては、空間充填(あるいは平面充填)のできない多面体(あるいは多角形)が除かれる(たとえば H3 は正十二面体あるいは双対である二十面体に対応するが、これは空間を充填することができない。また、H4 は正120胞体またはその双対である正600胞体が対応するが、これも4次元空間充填不能である。I2(p) は正 p-角形が対応するから、これも p = 3, 4, 6 の場合を除いて平面を敷き詰めることはできない(正三角形、正方形、正六角形ならば充填可能である)。
更なる留意点だが、(有向)ディンキン図形 Bn および Cn は同じワイル群を(したがってコクセター群も)生じる。これは、これらが「有向」グラフとしては異なるが、「無向」グラフとしては一致するためである。グラフの向きはルート系にとっては意味があるがワイル群にとってはそうではない、これは超立方体と交叉多胞体が正多胞体としては異なるのに同じ対称変換群を持つことに対応している。
性質
[編集]有限コクセター群のいくつかの性質について、表にして一覧する。
| 記号 | 別表記 | 括弧記法 | 階数 | 位数 | 対応する多胞体 | コクセター=ディンキン図形 |
|---|---|---|---|---|---|---|
| An | An | [3n] | n | (n + 1)! | n-次元単体 | |
| BCn | Cn | [4,3n-1] | n | 2n n! | n-次元超立方体 / n-次元交叉正多胞体 | |
| Dn | Bn | [3n-3,1,1] | n | 2n−1 n! | n-次元半超立方体 | |
| E6 | E6 | [32,2,1] | 6 | 72x6! = 51840 | 221, 122 | |
| E7 | E7 | [33,2,1] | 7 | 72x8! = 2903040 | 321, 231, 132 | |
| E8 | E8 | [34,2,1] | 8 | 192x10! = 696729600 | 421, 241, 142 | |
| F4 | F4 | [3,4,3] | 4 | 1152 | 正24胞体 | |
| G2 | - | [6] | 2 | 12 | 正六角形 | |
| H2 | G2 | [5] | 2 | 10 | 正五角形 | |
| H3 | G3 | [3,5] | 3 | 120 | 正二十面体/正十二面体 | |
| H4 | G4 | [3,3,5] | 4 | 14400 | 正120胞体/正600胞体 | |
| I2(p) | D2p | [p] | 2 | 2p | 正 p-角形 |
多胞体の対称変換群
[編集]一般次元正多胞体の対称変換群 (symmetry group) は必ず有限コクセター群になり、互いに双対な多胞体は同じ対称変換群を持つ。
任意の次元において、三種類の正多面体の系列を考えることができる。正 n-次元単体の対称変換群は対称群 Sn+1 であり、これを An 型のコクセター群という。n-次元超立方体およびその双対である n-次元交叉多胞体の対称変換群は BCn 型のコクセター群であり、超八面体群とも呼ばれる。
二次元、三次元、四次元の例外的正多面体が上記以外のコクセター群に対応する。二次元の場合は、正多角形の対称変換群である二面体群が系列 I2(p) を成す。三次元であれば、正十二面体およびその双対である正二十面体の対称変換群 H3 が全二十面体群 (full icosahedral group) として知られる。四次元のときは、正24胞体・正120胞体・正600胞体という三種の特別な正多胞体が存在する。はじめの一つは F4 を対称変換群としてもち、残りの二つは互いに双対で対称変換群 H4 を共有する。
Dn, E6, E7, E8 型のコクセター群は、ある種の半正多胞体の対称変換群になる。
アフィンコクセター群
[編集]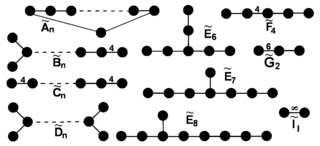
アフィン・コクセター群 (affine Coxeter groups) もコクセター群の重要なクラスである。アフィン・コクセター群はもはや有限群ではないが、しかしどれもそれを割った商が有限群となるような可換な正規部分群を含む。そしてどの場合でも、得られる剰余群はそれ自身コクセター群となる。アフィン・コクセター群のコクセター図形は対応する剰余群のコクセター図形に余分な頂点をひとつと辺をふたつ加えることによって得られる。例えば n ≥ 2 のとき、 n+1 個の頂点を円形に並べた形の図形が An からこの方法で得られ、対応するコクセター群として An 型のアフィン・ワイル群が得られる。特に n = 2 のとき、これは二等辺三角形による標準的な平面充填の対称変換群として図示することができる。
アフィン・コクセター群の一覧を以下に挙げる。
| 記号 | ヴィットの記号 | 括弧記法 | 対応する一様空間充填 | コクセター=ディンキン図形 |
|---|---|---|---|---|
| Pn+1 | [3[n+1]] | 斜交ハニカム格子 n = 2: 平面正三角形分割 n = 3: 四面体八面体ハニカム格子 |
||
| Sn+1 | [4,3n-2,31,1] | 半超立方体ハニカム格子 | ||
| Rn+1 | [4,3n-1,4] | 超立方体ハニカム格子 | ||
| Qn+1 | [ 31,1,3n-3,31,1] | 半超立方体ハニカム格子 | ||
| T7 | [32,2,2] | 222 | ||
| T8 | [33,3,1] | 331, 133 | ||
| T9 | [35,2,1] | 521, 251, 152 | ||
| U5 | [3,4,3,3] | 正16胞体ハニカム格子 正24胞体ハニカム格子 |
||
| V3 | [6,3] | 平面正六角形分割 平面正三角形分割 |
||
| W2 | [∞] | 正無限大角形 (apeirogon) |
下付の添字はどの場合も頂点数より 1 だけ少なくなっているが、それはこれらが有限の場合のコクセター図形から頂点をひとつ加えて得られることに由来する。
双曲コクセター群
[編集]双曲空間における鏡映群(特に双曲三角群が含まれる)を記述する双曲コクセター群が無限に存在する。
元の長さとブリュア順序
[編集]対合からなる生成系を一つ選べば、コクセター群上に長さ函数 l を考えることができるようになる。つまり、群の元を生成元をアルファベットとする語として表示するために必要な生成元の数の最小値(ケイリーグラフにおける語の距離にちょうど一致する)を、その元の長さとするのである。各元 v の表示のうち、l(v) 個の生成元の積となっているものを v の簡約表示(最短表示)という。例えば、S3 における互換 (1 3) は二つの簡約表示 (1 2)(2 3)(1 2) および (2 3)(1 2)(2 3) を持つ。また、写像
は、対称群上の符号函数を生成する。また有限コクセター群には最長の長さを持つ元が唯ひとつ存在する。これを最長元という。
簡約表示を使えば、コクセター群上に(左/右)弱順序、絶対順序、ブリュア順序(フランソワ・ブリュアに因む)という三種類の半順序を定義することができる。元 v がブリュア順序に関して元 u 以上であるというのを、v のある簡約表示が u のある簡約表示を部分文字列として含むときにいう(v のある簡約表示というのを v の任意の簡約表示としても同値である)。ただしこの場合は、使わない文字が(どの位置にでも)あってよい。右(左)弱順序の場合は、v ≥ u という関係を v の簡約表示が u の簡約表示を最初(最後)の部分に含むことと定める。語の長さを考えることによって、コクセター群は次数付き半順序集合となる。これらの順序に対応するハッセ図も研究の対象となり、また生成元から決定されるケイリーグラフとも関係する。絶対順序は弱順序と同様に定義されるが、そのアルファベットはコクセター群の生成系の任意の共役の全体からなる。[訳語疑問点]
例えば S3 の置換 (1 2 3) は、ただ一つの簡約表示 (1 2)(2 3) を持つから、ブリュア順序では (1 2) と (2 3) の上にあるけれども、弱順序に関しては (1 2) の上にあるだけということになる。
ホモロジー
[編集]コクセター群 W は有限個の位数 2 の元で生成されるから、そのアーベル化は基本アーベル 2-群(つまり巡回群 Z/2Z のいくつかのコピーの直和に同型)である。これは W の一次のホモロジー群の言葉に読み替えられる。
二次のホモロジー群に関係するシューア乗因子 M(W) は、有限鏡映群については (Ihara & Yokonuma 1965) で、アフィン鏡映群については (Yokonuma 1965) で計算されている。(Howlett 1988) も参照。いずれの場合においても、そのシューア乗因子は基本アーベル 2-群である。有限またはアフィンのワイル群からなるいかなる無限族 {Wn} も M(W) の階数は n を無限大に飛ばした極限で安定である。
関連項目
[編集]- ビルディング (数学)
- コクセター群の同型問題
- アルティン群
- 三角群
- コクセター元
- 複素鏡映群
- シュバレー・シェパード・トッドの定理
- ヘッケ環: 群環の量子変形
- カジュダン-ルスティック多項式
- コクセター群の最長元
脚注
[編集]参考文献
[編集]書籍
[編集]- Bourbaki, Nicolas (2002). Lie Groups and Lie Algebras: Chapter 4-6. Elements of mathematics. Springer-Verlag. ISBN 978-3-540-69171-6
- Humphreys, James E. (1990). Reflection Groups and Coxeter Groups. Cambridge studies in advanced mathematics. 29. Cambridge University Press. ISBN 0-521-37510-X
- Grove, Larry C.; Benson, T. (1985). Finite Reflection Groups. Graduate Texts in Mathematics. 99 (Second ed.). Springer. ISBN 0-387-96082-1
- Davis, Michael W. (2007), The Geometry and Topology of Coxeter Groups, ISBN 978-0-691-13138-2
- Richard Kane, Reflection Groups and Invariant Theory, CMS Books in Mathematics, Springer (2001)
- Anders Björner and Francesco Brenti, Combinatorics of Coxeter Groups, Graduate Texts in Mathematics, vol. 231, Springer, (2005)
- Howard Hiller, Geometry of Coxeter groups. Research Notes in Mathematics, 54. Pitman (Advanced Publishing Program), Boston, Mass.-London, 1982. iv+213 pp. ISBN 0-273-08517-4
- ポール・ギャレット Buildings and Classical Groups, Chapman & Hall/CRC.(1997年)ISBN 0-412-06331-X. ([1] にPSファイルがある)
論文
[編集]- Coxeter, H.S.M. (1934), “Discrete groups generated by reflections”, Ann. Of Math. 35 (3): 588–621, doi:10.2307/1968753, JSTOR 1968753
- Coxeter, H.S.M. (1935), “The complete enumeration of finite groups of the form ”, J. London Math. Soc. 10: 21–25
- Howlett, Robert B. (1988), “On the Schur Multipliers of Coxeter Groups”, Journal of the London Mathematical Society, 2 38 (2): 263–276, doi:10.1112/jlms/s2-38.2.263
- Vinberg, E. B. (1984), “Absence of crystallographic groups of reflections in Lobachevski spaces of large dimension”, Trudy Moskov. Mat. Obshch. 47
- Ihara, S.; Yokonuma, Takeo (1965), “On the second cohomology groups (Schur-multipliers) of finite reflection groups”, Jour. Fac. Sci. Univ. Tokyo, Sect. 1 11: 155–171, doi:10.15083/00039892
- Yokonuma, Takeo (1965), “On the second cohomology groups (Schur-multipliers) of infinite discrete reflection groups”, Jour. Fac. Sci. Univ. Tokyo, Sect. 1 11: 173–186
外部リンク
[編集]- Weisstein, Eric W. "Coxeter group". mathworld.wolfram.com (英語).















