クイックセレクト
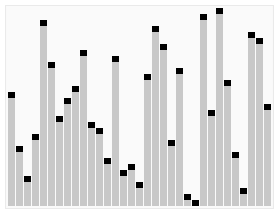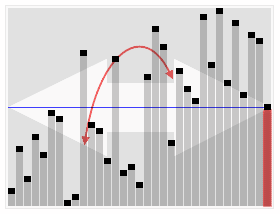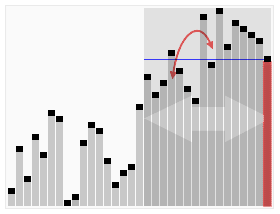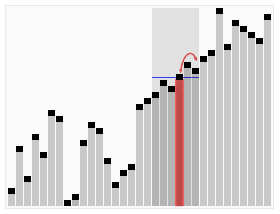 クイックセレクトの可視化。22番目に小さい要素を選択する | |
| クラス | 選択アルゴリズム |
|---|---|
| データ構造 | 配列 |
| 最悪計算時間 | О(n2) |
| 最良計算時間 | (n) |
| 平均計算時間 | (n) |
クイックセレクト(英: quickselect)は配列内の k 番目に小さい要素を見つけるための選択アルゴリズム。クイックソートによく似たアルゴリズムで、クイックソートと同じくアントニー・ホーアに発見されたため、 ホーアの選択アルゴリズムとも呼ばれる。 [1]クイックソートと同様に、平均的なパフォーマンスは良好だが、最悪の場合のパフォーマンスは悪くなる。クイックセレクトとその派生アルゴリズムは、効率的な実装として最もよく使われる選択アルゴリズムである。
クイックセレクトは、クイックソートと同じように1つの要素をピボットとして選択し、ピボットに基づいてデータをピボットよりも小さいかに大きいか二分割するのを繰り返す。ただし、クイックソートのように分割した両方の区間に対して再帰するのではなく、クイックセレクトは一方の側、つまり検索している要素のある側にのみ再帰する。これにより、平均計算量が軽減される。平均計算量はクイックソートが なのに対してクイックセレクトは 。最悪計算量はクイックソートと同じく 。
クイックソートと同様に、クイックセレクトは通常、In-placeアルゴリズムとして実装され、 k 番目の要素を選択するだけでなく、データを部分的にソートする。ソートとの関係の詳細については、選択アルゴリズムを参照。
アルゴリズム
[編集]クイックソートでは、線形時間で配列(インデックスの left から right への範囲)を特定の要素(ピボット)より小さい要素の部分配列と等しいかより大きい要素の部分配列へ分割し(partition)、部分配列にも繰り返し分割処理を行うことで目的の配列を整列させる。例えば要素 list[pivotIndex] をピボットとしてパーティションを実行する擬似コードは次のとおり:
function partition(list, left, right, pivotIndex) is
pivotValue := list[pivotIndex]
swap list[pivotIndex] and list[right] // ピボットを末尾に動かす
storeIndex := left
for i from left to right − 1 do
if list[i] < pivotValue then
swap list[storeIndex] and list[i]
increment storeIndex
swap list[right] and list[storeIndex] // ピボットを終了時の位置に動かす
return storeIndex
これはロムトの分割法として知られている。ロムトの方法は、ホーアの分割法よりも要素の交換(swap)を行う回数が多くなるため、一般にはホーアの方法がより高速であると考えられている。しかし、投機的実行を考慮すると実際にはロムトの方法がホーアの方法より速くなる場合がある。 また、ホーアの方法は双方向イテレータを要求するが、ロムトの方法は前方イテレータのみを要求するという違いがある(例えば片方向リストのソート)。[2]
クイックソートでは、分割後の両方の範囲を再帰処理するため最良の時間計算量は である。しかし選択アルゴリズムでは、目的の要素がピボットより後ろにあるか前にあるかは事前に分かるため、ソートと異なり片方の範囲のみを再帰呼び出しをすることで、最終的に目的の要素を正しい位置に置くことができる。これがクイックセレクトである。
// リストの left 以上 right 以下の位置にあることが分かっている k 番目の要素を返す(left <= k <= right).
function select(list, left, right, k) is
if left = right then // 残りの要素が一つなら
return list[left] // その要素を返す
pivotIndex := ... // left と right の間から pivotIndex を決める
// 例えば、 left + floor(rand() % (right − left + 1))
pivotIndex := partition(list, left, right, pivotIndex)
// ピボットは、パーティション終了時の位置に移動してる
if k = pivotIndex then
return list[k]
else if k < pivotIndex then
return select(list, left, pivotIndex − 1, k)
else
return select(list, pivotIndex + 1, right, k)
クイックセレクトは線形時間で終わることが期待される優れたパフォーマンスのアルゴリズムである。クイックセレクトはインプレースアルゴリズムでもあり、末尾呼び出し最適化がかかる場合や、以下のようにループで末尾再帰を排除した実装を行う場合は、定数のメモリ空間で実行できる。
function select(list, left, right, k) is
loop
if left = right then
return list[left]
pivotIndex := ... // select pivotIndex between left and right
pivotIndex := partition(list, left, right, pivotIndex)
if k = pivotIndex then
return list[k]
else if k < pivotIndex then
right := pivotIndex − 1
else
left := pivotIndex + 1
時間計算量
[編集]クイックソートと同様に、クイックセレクトは平均パフォーマンスは良好だが、これは選択されたピボットに左右される。適切なピボットが選択された場合、つまり、検索する区間が一定の割合で一貫して減少する場合、検索セットのサイズは指数関数的に減少し、等比数列の和の公式から考えると、各ステップが線形であり、全体としても線形時間となる。ただし、毎回1つの要素だけ減少するなど、不適切なピボットが一貫して選択されている場合、最悪の場合のパフォーマンスの2次関数 となる。 これは、たとえば、区間の最大要素をピボットとして使用するようなクイックセレクトをソート済みの配列に使用した場合に発生する。ランダムにピボットを選ぶ場合、最悪のケースが発生する確率は指数関数的に減少するため時間計算量はほとんど確実に になる。
派生
[編集]ほとんど確実に線形時間で処理をする簡単な解決策は、ランダムにピボットを選択することである。
決定的な手法としては、クイックソートのように3要素(例えば、先頭・中央・末尾)の中央値をピボットに選ぶ戦略が有効である。これにより、現実でよくある部分的にソートされたデータに対して線形のパフォーマンスが得られる。ただし、不自然な並びでは依然として最悪計算量になる可能性がある。 David Musserは、その戦略に対する攻撃を可能にする「3要素の中央値キラー」シーケンスについて説明している。彼はこれを動機としてイントロセレクトを開発した。
より洗練されたピボット戦略を使用することで、最悪の場合でも線形パフォーマンスを保証できる。これを実現できるのが中央値の中央値だが、ピボットの計算のオーバーヘッドは高いため、実際にはあまり使用されない。始めはクイックセレクトを使って、ある程度の回数で終了しなかった場合に中央値の中央値を使うことで、高速の平均ケースパフォーマンスと線形の最悪ケースパフォーマンスの両方を達成できる。この手法を使うのがイントロセレクトである。
平均時間計算量についてより細かく計算すると、少なくとも 以下である(これは中央値の場合で、他のkの方が高速)。 [3]フロイド・リベストのアルゴリズムではより複雑なピボット戦略によって 3/2 の改善を果たしている。この場合、 となる(これは中央値の場合で、他のkの方が高速)。
関連項目
[編集]出典
[編集]- ^ Hoare, C. A. R. (1961). “Algorithm 65: Find”. Comm. ACM 4 (7): 321–322. doi:10.1145/366622.366647.
- ^ Alexandrescu, Andrei (2020年5月14日). “Lomuto's comeback”. dlang.org. 2022年3月23日閲覧。
- ^ Blum-style analysis of Quickselect, David Eppstein, October 9, 2007.
外部リンク
[編集]- " qselect "、 Matlab、ManolisLourakisのクイックセレクトアルゴリズム









