コンテンツにスキップ

英文维基 | 中文维基 | 日文维基 | 草榴社区

き裂閉口

出典: フリー百科事典『ウィキペディア（Wikipedia）』

材料の疲労、特に金属疲労におけるき裂閉口（きれつへいこう、英: crack closure）とは、き裂を開こうとする力が加わっても、ある程度以上の力まではき裂が閉じた状態を保つ現象である[1][2][3]。き裂開閉口[1]、き裂開閉口現象[4]、き裂開閉口挙動[5]などとも呼ばれる。疲労き裂伝ぱに影響を与える重大因子の一つである。1970年・1971年に、ヴォルフ・エルバ― (Wolf Elber) によって最初に発見された。

き裂閉口現象から、実際にき裂が開口している範囲に相当する応力拡大係数の範囲が導かれる。これは有効応力拡大係数範囲（ゆうこうおうりょくかくだいけいすうはんい、英: effective stress intensity range）と呼ばれ、疲労き裂伝ぱ速度特性を本質的に決定する駆動力となる。き裂閉口の原因の一つは、き裂縁に残留引張塑性変形域によるもので、このような機構のき裂閉口は塑性誘起き裂閉口と呼ばれる。この他の機構のき裂閉口として、酸化物誘起き裂閉口、破面粗さ誘起き裂閉口、粘性流体誘起き裂閉口、相変態誘起き裂閉口が存在する。

背景

[編集]

金属材料の疲労き裂の伝ぱ速度は、小規模降伏条件が満たされる範囲内では応力拡大係数範囲 ΔK に強く依存することが知られている[6]。理想的な弾性体中のき裂を想定すると、引張りの外力がかかるとき裂は開口し、除荷して外力0になるとき裂は閉口する[5]。き裂の応力拡大係数でいえば、KI > 0 のときにき裂は開口しており、KI = 0 でき裂が閉口する[5]。

このような単純なき裂開閉口を前提にすると、疲労き裂伝ぱ特性を整理するための応力拡大係数範囲 ΔK は次のように仮定できる[7]。

   (Kmin > 0 の場合)
  (Kmin ≤ 0 の場合)

実際の疲労で進展するき裂も、引張荷重下では開口して圧縮荷重下で閉口すると以前までは考えられてきた[8][9]。

き裂閉口の発見と有効応力拡大係数範囲

[編集]
繰り返し荷重中のき裂開閉口の概念図。理想弾性体中のき裂（中央）は引張荷重下で常に開口するに対し、き裂閉口を起こしている疲労き裂（右）では一定引張荷重まで開口しない。

しかし、1970年[10]・1971年[11]に、ヴォルフ・エルバ― (Wolf Elber) によって、引張りの外力がかかった状態でもき裂が閉じる現象が初めて発見された[12][13]。この現象の実在は、その後多くの研究者たちによって確認された[14]。現在では、き裂閉口は疲労き裂伝ぱに影響を与える重大因子に位置づけられる[15]。

き裂閉口を発見したエルバ―は、き裂の伝ぱ挙動を議論するにはき裂の真の開閉口挙動に対応する応力拡大係数の幅、すなわち有効応力拡大係数範囲（英: effective stress intensity range）ΔKeff を用いる必要があるとは指摘した[16]。有効応力拡大係数範囲とは、繰り返し応力拡大係数の最大値 Kmax からき裂が開口し始める時の応力拡大係数 Kop を差し引いたもので、次式で定義される[8]。

き裂が閉口し始める時の応力拡大係数 Kcl を用い、次式のように ΔKeff を定義する場合もある[17]。

実際には Kcl とKop を区別しない研究も多い[18]。ただし、精密には Kcl とKop は異なる[18]。

また、き裂閉口の程度を表すパラメータとして、次のき裂開口比（英: crack opening ratio）U が定義される[19]。

一般に、ある垂直応力 σ がき裂に作用するとき、そのときの応力拡大係数 K は

と表すことができる[20][21]。ここで、a はき裂長さ、Y は部材形状や負荷形態などで決まる修正係数である[20][21]。このような関係にもとづいて応力拡大係数範囲と応力範囲を形式的に対応させると、き裂開口比 U は

とも表される[22]。有効応力拡大係数範囲は U を用いて

とも表される[8]。

以上のような有効応力拡大係数範囲 ΔKeff は、き裂先端が真に開口している間の応力拡大係数範囲に対応し、今日ではき裂伝ぱの駆動力を表現する重要なパラメータに位置する[23]。

疲労き裂伝ぱ速度

[編集]

上記のように金属材料の疲労き裂の伝ぱ速度は、小規模降伏条件が満たされる範囲内では応力拡大係数範囲 ΔK に強く依存することが知られている[6]。繰り返し荷重一回当たりの疲労き裂の伝ぱ量を da/dN とし、da/dN と ΔK の関係を両対数グラフで整理すると、その関係は一般的に逆S字型の曲線となる[24]。 da/dN-ΔK 図は、さらに下限界近傍領域（第IIa段階）、中間領域（第IIb段階）、上限界近傍領域（第IIc段階）と呼ばれる3つの領域に分かれる[24][25]。ΔK が中レベルの中間領域では、関係曲線は直線状となる[26]。ΔK が高レベルの上限界近傍領域では、き裂伝ぱ速度が直線から逸脱するようにして急上昇する[26]。ΔK が低レベルの下限界近傍領域では、き裂伝ぱ速度が直線から逸脱するようにして急減少し、ある ΔK で da/dN が 0 となる[26]。この事実上き裂が停止する ΔK の値は下限界応力拡大係数範囲と呼ばれ、ΔKth と表わされる[27]。

da/dN 対 ΔK の関係が直線となる中間領域においては、パリス則として知られる次のような式で疲労き裂伝ぱ速度 da/dN を表すことができる[28]。

ここで、C と m は材料定数とされる[28]。

一方で、疲労き裂伝ぱ速度 da/dN は応力比 R にも強く依存する[29]。応力比 R は

と定義されるパラメータで、平均応力の存在を代表する[30][29]。実際の da/dN-ΔK の関係は応力比に依存し、同じ材料であっても応力比が違えば da/dN-ΔK 関係も違う曲線となる[31]。パリス則の C や m も実際には応力比への依存性がある[29]。

このように応力比 R ごとに異なっていた疲労き裂伝ぱ速度特性を、有効応力拡大係数範囲 ΔKeff を使って整理し直すと、R の値と無関係に da/dN-ΔKeff 関係は一つの曲線にまとまる[32]。したがって、応力比の影響はき裂閉口の影響として理解することができ[33]、da/dN-ΔKeff 関係は da/dN-ΔK よりも本質的な疲労き裂伝ぱ速度特性を表しているといえる[34]。有効応力拡大係数範囲を使い、パリス則も

のように修正される[35]。

疲労き裂伝ぱ速度 da/dN を ΔKeff で整理すると、直線状の中間領域はより低い da/dN の領域まで広がる傾向にある[36]。しかし、それでも ΔKeff が低レベルになると da/dN が急激に低下してき裂伝ぱが停まる ΔKeff の下限が存在する[37][36]。この下限の ΔKth は下限界有効応力拡大係数範囲と呼ばれ、ΔKeff, th などと表される[38]。ΔKth の数値が応力比、荷重履歴、環境などの影響を受けて変化しやすいのに対し、ΔKeff, th の数値は比較的安定しており、材料固有の定数により近いと考えられている[39]。鉄鋼材料の場合では、ΔKeff, th は 2 MPa⋅m1/2 から 4 MPa⋅m1/2 の値を取る[36]。

機構による分類

[編集]

発生の原因・機構により、き裂閉口は塑性誘起き裂閉口、酸化物誘起き裂閉口、破面粗さ誘起き裂閉口、粘性流体誘起き裂閉口、相変態誘起き裂閉口に細分される[40][41][14]。

塑性誘起き裂閉口
残留引張変形を閉口の原因とするき裂閉口で、き裂閉口を最初に発見したエルバ―が唱えた機構でもある[42]。一般的な金属材料に荷重が加わると、き裂先端の高い応力のため、き裂先端で塑性降伏が起きてき裂先端には塑性域が形成される[43][44]。き裂が疲労で進展すると、そのき裂自身が作った先端塑性域を切って進展することになる[9]。その結果、き裂先端よりも後方にも、き裂縁に引張塑性変形域が残留する[9]。この状態で除荷すると、これら残留引張塑性域の伸びの分だけき裂は早く閉口し、引張荷重がまだかかっている状態でもき裂が閉口するようになる[9][45]。このような機構のき裂閉口が塑性誘起き裂閉口と呼ばれる[46][45]。弾塑性材料であれば一般的に起こり得る種類のき裂閉口である[45]。
酸化物誘起き裂閉口
き裂が進展して新たにできた破面は、湿り空気によって酸化する[47]。とくに、上下破面の接触の結果、フレッティングによって破面に酸化層が集積することがある[47]。このような酸化層が詰め物として働き、き裂を閉口させるのが、酸化物誘起き裂閉口の機構である[48]。酸化物誘起き裂閉口の働きは、特に下限界近傍領域で顕著になる[48]。腐食疲労で下限界近くでのき裂伝ぱ速度が大気中よりも遅いことがあるが、これも酸化物誘起き裂閉口によって起こると考えられている[49]。
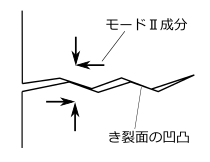
破面粗さ誘起き裂閉口
き裂上下面が面内方向に互い違いにせん断変形するようなき裂の変形様式をモードIIと呼ぶ[50]。モードIIがき裂伝ぱに関わるとき、き裂破面の凹凸が原因となって、負荷時には破面が完全に離れるのが遅れ、除荷時には破面同士の接触が早まることがある[51]。酸化物誘起き裂閉口と同様に、破面粗さ誘起き裂閉口の働きは特に下限界近傍領域で顕著になる[48]。
粘性流体誘起き裂閉口
油のような粘性流体がき裂破面に存在するときに、油の圧力でき裂破面がある程度以上は閉じなくなることがある[52]。このような機構のき裂閉口を粘性流体誘起き裂閉口という[53]。ただし油中のき裂伝ぱでは、酸化の抑制による酸化物誘起き裂閉口の最小化や環境脆化の抑制なども起こし、油中のき裂伝ぱの最終的な結果はいくつかの競合的な因子がからむ[54]。そのため、油中のき裂伝ぱでは粘性流体誘起き裂閉口によっていつもき裂伝ぱ速度が下がるとはならない[53]。また、他のき裂閉口の機構と比して、このき裂閉口の重要性は低いともいわれる[54][53]。
相変態誘起き裂閉口
準安定オーステナイト組織などの加工誘起マルテンサイト変態を起こす材料では、き裂先端が局部組成変形によって相変態を起こし、体積が増加する[53]。この変態・体積増加した領域が疲労き裂の後方に残されていくと、この領域が周囲から圧縮残留応力を受けてき裂の開口が抑制される[54][53]。このような機構のき裂閉口を相変態誘起き裂閉口という[53]。残留応力がき裂を閉口させるという点において、塑性誘起き裂閉口と共通する[55]。
  • 各々のき裂閉口の概略図
  • 塑性誘起き裂閉口
    塑性誘起き裂閉口
  • 酸化物誘起き裂閉口
    酸化物誘起き裂閉口
  • 破面粗さ誘起き裂閉口
    破面粗さ誘起き裂閉口
  • 粘性流体誘起き裂閉口
    粘性流体誘起き裂閉口
  • 相変態誘起き裂閉口
    相変態誘起き裂閉口

測定

[編集]
コンプライアンス法によるき裂閉口測定の概略図

き裂閉口現象は、試験片などを用いた測定で確認することができる[56]。もっとも一般的な測定方法は、コンプライアンス法と呼ばれる試験片のコンプライアンスの変化を利用する方法である[57][58]。試験片に対して荷重をかけるとき、荷重 P と荷重点の荷重方向変位 δ の関係は、き裂先端の塑性変形が無視可能な範囲でほぼ線形となる[56]。このときの λ = δ/P をコンプライアンスと呼ぶ[57]。き裂開閉口を起こしている試験片に荷重を加えると、き裂が開閉口したタイミングで試験片断面が変化してコンプライアンスが変化する[57]。よって、コンプライアンス変化を測定することにより、き裂閉口現象の検出が可能となる[57]。

実際の試験では、荷重点の荷重方向変位 δ の代わりに、それに対応関係を持つ他の場所の変位やひずみが用いられる[57][59]。き裂を発生させる切欠きにクリップゲージを設置して変位を得る方法や、試験片背面側にひずみゲージを設置してひずみを得る方法などがよく使われている[59]。き裂開閉口が生じている場合の荷重（または応力、応力拡大係数）と変位（またはひずみ）の関係曲線を得ると、き裂が完全に開いている高荷重範囲の曲線はほぼ線形となっているが、それよりも荷重を下げていくとあるところから曲線が折れ曲がって傾きが変化する[56][60][61]。この傾き変化がコンプライアンス変化なので、曲線が折れ曲がる点がき裂開閉口点に相当する[60]。ただし、実際には傾き変化は小さく折れ曲がり点は不明瞭なため、き裂が完全開口した範囲の荷重-変位曲線を線形と仮定して試験荷重全域に延長し、き裂完全開口に相当する変位を実測した変位から差し引くことで、折れ曲がり点を明瞭にする手法が取られる[60][62][63]。

き裂開閉口を実測する他の方法には、き裂開閉口にともなう電気抵抗の変化を利用する方法や、き裂破面での超音波の透過あるいは反射を利用する方法などがある[64]。透明な高分子材料などに限定されるが、光学的な干渉を利用し、材料内部も含めて3次元的にき裂開閉口の挙動を調べた例もある[65][59]。

予測・計算モデル

[編集]

き裂閉口の程度は、材料の微視組織、環境、応力状態、負荷履歴、き裂サイズによって左右される[66]。多くの場合、き裂閉口の程度はそれぞれのき裂伝ぱ時の状況に依存する[67]。また、上記のような複数の機構がき裂閉口に係わり、き裂伝ぱ速度に影響を及ぼす可能性もある[68]。こういった複雑な問題が存在するため、き裂閉口の定量的な理論の確立は難しい[67]。有効応力拡大係数範囲 ΔKeff の正確な予想方法は未だ確立できておらず、今後の研究課題である[36]。現状では ΔKeff を知るにはき裂開閉口を実測する必要があるので、実際の機械や構造物に存在するき裂の ΔKeff を求めることは容易ではない[69]。

き裂開口応力拡大係数 Kop も、材料定数というよりは、多数の因子によって決まる値だと考えられている[70]。エルバ―はアルミニウム合金2023-T3について Kop を測定し、き裂開口比 U の経験式を応力比 R を変数として次のように求めた[71][70]。

   (ただし −0.1 ≤ R ≤ 0.7 の範囲)

他の研究者も、他の合金で似たような経験式を求めた[70][72]。塑性誘起き裂閉口の場合は、このように U には高い可能性で R 依存性がある[71]。一方で、エルバ―の式についても他の経験式についても簡易化が過剰と指摘されており、U の決定には R 以外の因子もあると指摘されている[70]。

塑性誘起き裂閉口については、有限要素法などの力学的な解析モデルによる研究が比較的進んでいる[42]。有限要素法を用いた計算によって、理想き裂の進展とともに開口応力 σop が増加する結果や[73]、平面ひずみ状態でのき裂閉口の度合いは平面応力状態よりも低下するといった結果が得られている[74]。

出典

[編集]
  1. ^ a b 日本機械学会 1997, p. 317.
  2. ^ Anderson 2011, p. 472.
  3. ^ 小林 1993, p. 134.
  4. ^ 城野・宋 2005, pp. 4, 15.
  5. ^ a b c 東郷 2013, p. 145.
  6. ^ a b 大路・中井 2006, p. 94.
  7. ^ 小林 1993, p. 132.
  8. ^ a b c 日本材料学会（編） 2008, p. 166.
  9. ^ a b c d 陳 2015, p. 99.
  10. ^ Wolf Elber (1970). “Fatigue crack closure under cyclic tension”. Engineering Fracture Mechanics 2 (1): 37-45. doi:10.1016/0013-7944(70)90028-7. 
  11. ^ W. Elber (1971). “The Significance of Fatigue Crack Closure”. Damage Tolerance in Aircraft Structures, ASTM STP 486: 230–242. doi:10.1520/STP26680S. ISBN 978-0-8031-0031-2. 
  12. ^ Anderson 2011, pp. 472, 521.
  13. ^ 城野・宋 2005, p. 4.
  14. ^ a b Anderson 2011, p. 473.
  15. ^ 城野・宋 2005, p. 5.
  16. ^ 大路・中井 2006, pp. 101–102.
  17. ^ 陳 2015, p. 102.
  18. ^ a b 陳 2015, p. 103.
  19. ^ 東郷 2013, pp. 146–147.
  20. ^ a b 東郷 2013, pp. 82–83.
  21. ^ a b 小林 1993, pp. 64–65.
  22. ^ 中井・久保 2014, pp. 96–99.
  23. ^ 日本機械学会 1997, p. 1315.
  24. ^ a b 陳 2015, pp. 95–96.
  25. ^ 日本材料学会（編） 2008, p. 159.
  26. ^ a b c Anderson 2011, p. 469.
  27. ^ 日本材料学会（編） 2008, p. 160.
  28. ^ a b 東郷 2013, p. 144.
  29. ^ a b c スレッシュ 2005, p. 328.
  30. ^ 東郷 2013, p. 138.
  31. ^ 日本材料学会（編） 2008, p. 168.
  32. ^ 大路・中井 2006, p. 102.
  33. ^ 日本材料学会（編） 2008, p. 169.
  34. ^ 東郷 2013, p. 148.
  35. ^ 城野・宋 2005, pp. 10–11.
  36. ^ a b c d 中井・久保 2014, p. 115.
  37. ^ Anderson 2011, pp. 482–483.
  38. ^ 日本材料学会（編） 2008, p. 183.
  39. ^ 日本材料学会（編） 2008, p. 182.
  40. ^ スレッシュ 2005, p. 479.
  41. ^ 城野・宋 2005, p. 16.
  42. ^ a b 城野・宋 2005, p. 15.
  43. ^ 東郷 2013, p. 89.
  44. ^ 中井・久保 2014, p. 37.
  45. ^ a b c 東郷 2013, p. 149.
  46. ^ 陳 2015, pp. 99–100.
  47. ^ a b スレッシュ 2005, p. 491.
  48. ^ a b c 陳 2015, p. 100.
  49. ^ 中井・久保 2014, pp. 161–162.
  50. ^ 小林 1993, p. 63.
  51. ^ 城野・宋 2005, pp. 17–18.
  52. ^ 城野・宋 2005, p. 18.
  53. ^ a b c d e f 城野・宋 2005, p. 19.
  54. ^ a b c スレッシュ 2005, p. 498.
  55. ^ Anderson 2011, p. 475.
  56. ^ a b c 陳 2015, p. 101.
  57. ^ a b c d e 城野・宋 2005, p. 28.
  58. ^ Anderson 2011, p. 511.
  59. ^ a b c Anderson 2011, p. 512.
  60. ^ a b c 城野・宋 2005, p. 37.
  61. ^ スレッシュ 2005, p. 482.
  62. ^ 陳 2015, pp. 101–102.
  63. ^ スレッシュ 2005, p. 483.
  64. ^ 城野・宋 2005, pp. 28–32.
  65. ^ 城野・宋 2005, p. 36.
  66. ^ スレッシュ 2005, pp. 500–501.
  67. ^ a b スレッシュ 2005, p. 500.
  68. ^ スレッシュ 2005, p. 501.
  69. ^ 日本材料学会（編） 2008, p. 172.
  70. ^ a b c d Anderson 2011, p. 478.
  71. ^ a b 城野・宋 2005, p. 11.
  72. ^ 城野・宋 2005, p. 62.
  73. ^ 中井・久保 2014, p. 102.
  74. ^ スレッシュ 2005, p. 488.

参照文献

[編集]

外部リンク

[編集]
「https://ja-two.iwiki.icu/w/index.php?title=き裂閉口&oldid=96195732」から取得