加算性白色ガウス雑音 (かさんせいはくしょくがうすざつおん、Additive white Gaussian noise、AWGN ) は自然界で発生する多数のランダム過程の効果を模倣する目的で、情報理論で用いられる基本的ノイズモデル。その修飾語は固有の特性を表している。
加算性 白色 ガウス 正規分布 にしたがうことを意味する。広域帯の雑音は、導体中の原子の熱振動(熱雑音 もしくはジョンソン・ナイキスト・ノイズ と呼ばれる)などの多くの自然発生源、ショットノイズ 、地球や他の温かい物体による黒体輻射 、太陽 などによる天体 源によるものである。確率論 における中心極限定理 は、多くのランダム過程の総和が正規分布(ガウス分布)になる傾向にあることを示している。
AWGNは、通信に対する唯一の障害が、一定のスペクトル密度 (帯域幅 1ヘルツ 毎のワットで表される)及びガウス分布 の振幅を持つ広帯域 もしくは白色 の雑音の線形加算である通信路のモデルとして用いられる。このモデルは、フェージング 、周波数 選択性、干渉 (通信) 、非線形性 、分散 (光学) を考慮に入れていない。しかし、これらの他の現象を考慮する前に、系の基本的な振る舞いについての洞察を得るために有益な、単純で扱いやすい数学的なモデルである。
AWGNは多くの衛星 と深宇宙通信の繋がりのいいモデルである。マルチパス、地形による遮断、干渉などの理由から、殆どの陸上における繋がりに対してはいいモデルではない。しかし、地上経路のモデリングにおいては、現代の無線システムが地上で運用しているときに遭遇するマルチパス、地形による遮断、干渉、地面クラッタ、自己干渉に加え、研究中である通信路の背景雑音をシミュレートするために一般的に使用されている。
AWGNの通信路は離散時間の事象の添え字
i
{\displaystyle i}
Y
i
{\displaystyle Y_{i}}
Y
i
{\displaystyle Y_{i}}
X
i
{\displaystyle X_{i}}
Z
i
{\displaystyle Z_{i}}
Z
i
{\displaystyle Z_{i}}
独立同分布 であり、平均0、分散
N
{\displaystyle N}
正規分布 から得られるものである。さらに
Z
i
{\displaystyle Z_{i}}
X
i
{\displaystyle X_{i}}
Z
i
∼
N
(
0
,
N
)
{\displaystyle Z_{i}\sim {\mathcal {N}}(0,N)\,\!}
Y
i
=
X
i
+
Z
i
.
{\displaystyle Y_{i}=X_{i}+Z_{i}.\,\!}
雑音nが0ではなく、
X
i
{\displaystyle X_{i}}
(
x
1
,
x
2
,
…
,
x
k
)
{\displaystyle (x_{1},x_{2},\dots ,x_{k})}
1
k
∑
i
=
1
k
x
i
2
≤
P
,
{\displaystyle {\frac {1}{k}}\sum _{i=1}^{k}x_{i}^{2}\leq P,}
ここで
P
{\displaystyle P}
C
=
max
f
(
x
)
s.t.
E
(
X
2
)
≤
P
I
(
X
;
Y
)
{\displaystyle C=\max _{f(x){\text{ s.t. }}E\left(X^{2}\right)\leq P}I(X;Y)\,\!}
f
(
x
)
{\displaystyle f(x)}
X
{\displaystyle X}
I
(
X
;
Y
)
{\displaystyle I(X;Y)}
微分エントロピー の観点から書くと以下の式になる。
I
(
X
;
Y
)
=
h
(
Y
)
−
h
(
Y
|
X
)
=
h
(
Y
)
−
h
(
X
+
Z
|
X
)
=
h
(
Y
)
−
h
(
Z
|
X
)
{\displaystyle {\begin{aligned}I(X;Y)=h(Y)-h(Y|X)&=h(Y)-h(X+Z|X)&=h(Y)-h(Z|X)\end{aligned}}\,\!}
しかし
X
{\displaystyle X}
Z
{\displaystyle Z}
I
(
X
;
Y
)
=
h
(
Y
)
−
h
(
Z
)
{\displaystyle I(X;Y)=h(Y)-h(Z)\,\!}
となる。ガウスの微分エントロピー を評価すると
h
(
Z
)
=
1
2
log
(
2
π
e
N
)
{\displaystyle h(Z)={\frac {1}{2}}\log(2\pi eN)\,\!}
となる。
X
{\displaystyle X}
Z
{\displaystyle Z}
Y
{\displaystyle Y}
E
(
Y
2
)
=
E
(
(
X
+
Z
)
2
)
=
E
(
X
2
)
+
2
E
(
X
)
E
(
Z
)
+
E
(
Z
2
)
=
P
+
N
{\displaystyle E(Y^{2})=E((X+Z)^{2})=E(X^{2})+2E(X)E(Z)+E(Z^{2})=P+N\,\!}
この範囲より、微分エントロピーの性質を推測すると
h
(
Y
)
≤
1
2
log
(
2
π
e
(
P
+
N
)
)
{\displaystyle h(Y)\leq {\frac {1}{2}}\log(2\pi e(P+N))\,\!}
となる。よって通信路の容量は相互情報量 における達成可能な最大の境界で与えられ、
I
(
X
;
Y
)
≤
1
2
log
(
2
π
e
(
P
+
N
)
)
−
1
2
log
(
2
π
e
N
)
{\displaystyle I(X;Y)\leq {\frac {1}{2}}\log(2\pi e(P+N))-{\frac {1}{2}}\log(2\pi eN)\,\!}
I
(
X
;
Y
)
{\displaystyle I(X;Y)}
X
∼
N
(
0
,
P
)
{\displaystyle X\sim {\mathcal {N}}(0,P)\,\!}
のときに最大となり、このとき通信路容量
C
{\displaystyle C}
C
=
1
2
log
(
1
+
P
N
)
{\displaystyle C={\frac {1}{2}}\log \left(1+{\frac {P}{N}}\right)\,\!}
1
{\displaystyle 1}
M
{\displaystyle M}
M
{\displaystyle M}
n
{\displaystyle n}
R
{\displaystyle R}
R
=
log
M
n
{\displaystyle R={\frac {\log M}{n}}\,\!}
レートは、もし
n
{\displaystyle n}
C
{\displaystyle C}
N
{\displaystyle N}
n
{\displaystyle n}
N
{\displaystyle N}
n
(
N
+
ϵ
)
{\displaystyle {\sqrt {n(N+\epsilon )}}}
各符号ベクトルは、それに復号される受信符号ベクトルの関連する球を持ち、このような球は符号を一意に写像しなくてはならない。よって、これらの球は交差してはならないため、球充填 の問題に差し当たる。いくつの異なる符号が、
n
{\displaystyle n}
n
(
P
+
N
)
{\displaystyle n(P+N)}
n
(
P
+
N
)
{\displaystyle {\sqrt {n(P+N)}}}
n
N
{\displaystyle {\sqrt {nN}}}
n 次元での球の体積は
r
n
{\displaystyle r^{n}}
(
n
(
P
+
N
)
)
n
2
(
n
N
)
n
2
=
2
n
2
log
(
1
+
P
/
N
)
{\displaystyle {\frac {(n(P+N))^{\frac {n}{2}}}{(nN)^{\frac {n}{2}}}}=2^{{\frac {n}{2}}\log(1+P/N)}\,\!}
となる。この議論によりレートRは
1
2
log
(
1
+
P
/
N
)
{\displaystyle {\frac {1}{2}}\log(1+P/N)}
この節では最後の節からのレート上限の達成可能性について述べる。
エンコーダーにもデコーダーにも知られた暗号表は長さn、独立同一分布で正規分布、分散
P
−
ϵ
{\displaystyle P-\epsilon }
受け取られたメッセージは、コードブックに書かれている一意に結びついた典型的なメッセージへと復号される。 もし、そのようなメッセージが存在しない、もしくは、パワー制約に違反する場合、複合エラーが宣言される。
X
n
(
i
)
{\displaystyle X^{n}(i)}
i
{\displaystyle i}
Y
n
{\displaystyle Y^{n}}
出来事
U
{\displaystyle U}
P
{\displaystyle P}
出来事
V
{\displaystyle V}
出来事
E
j
{\displaystyle E_{j}}
(
X
n
(
j
)
,
Y
n
)
{\displaystyle (X^{n}(j),Y^{n})}
A
ϵ
(
n
)
{\displaystyle A_{\epsilon }^{(n)}}
i
≠
j
{\displaystyle i\neq j}
したがって、エラーは
U
{\displaystyle U}
V
{\displaystyle V}
E
i
{\displaystyle E_{i}}
P
(
U
)
{\displaystyle P(U)}
漸近等分割性 を結びつけることにより、
P
(
V
)
{\displaystyle P(V)}
n
{\displaystyle n}
P
(
U
)
{\displaystyle P(U)}
P
(
V
)
{\displaystyle P(V)}
ϵ
{\displaystyle \epsilon }
i
≠
j
{\displaystyle i\neq j}
X
n
(
i
)
{\displaystyle X^{n}(i)}
X
n
(
j
)
{\displaystyle X^{n}(j)}
X
n
(
i
)
{\displaystyle X^{n}(i)}
Y
n
{\displaystyle Y^{n}}
P
(
E
j
)
=
2
−
n
(
I
(
X
;
Y
)
−
3
ϵ
)
{\displaystyle P(E_{j})=2^{-n(I(X;Y)-3\epsilon )}}
P
e
(
n
)
{\displaystyle P_{e}^{(n)}}
P
e
(
n
)
≤
P
(
U
)
+
P
(
V
)
+
∑
j
≠
i
P
(
E
j
)
≤
ϵ
+
ϵ
+
∑
j
≠
i
2
−
n
(
I
(
X
;
Y
)
−
3
ϵ
)
≤
2
ϵ
+
(
2
n
R
−
1
)
2
−
n
(
I
(
X
;
Y
)
−
3
ϵ
)
≤
2
ϵ
+
(
2
3
n
ϵ
)
2
−
n
(
I
(
X
;
Y
)
−
R
)
≤
3
ϵ
{\displaystyle {\begin{aligned}P_{e}^{(n)}&\leq P(U)+P(V)+\sum _{j\neq i}P(E_{j})\\&\leq \epsilon +\epsilon +\sum _{j\neq i}2^{-n(I(X;Y)-3\epsilon )}\\&\leq 2\epsilon +(2^{nR}-1)2^{-n(I(X;Y)-3\epsilon )}\\&\leq 2\epsilon +(2^{3n\epsilon })2^{-n(I(X;Y)-R)}\\&\leq 3\epsilon \end{aligned}}}
となる。よって、n が無限大に近づくことにより、
P
e
(
n
)
{\displaystyle P_{e}^{(n)}}
R
<
I
(
X
;
Y
)
−
3
ϵ
{\displaystyle R<I(X;Y)-3\epsilon }
ここで、容量
C
=
1
2
log
(
1
+
P
N
)
{\displaystyle C={\frac {1}{2}}\log(1+{\frac {P}{N}})}
コードブックに対してパワー制約を満たし、さらにメッセージが一様分布に従うと仮定する。
W
{\displaystyle W}
W
^
{\displaystyle {\hat {W}}}
W
⟶
X
(
n
)
(
W
)
⟶
Y
(
n
)
⟶
W
^
{\displaystyle W\longrightarrow X^{(n)}(W)\longrightarrow Y^{(n)}\longrightarrow {\hat {W}}}
ファノの不等式 を利用して
H
(
W
|
W
^
)
≤
1
+
n
R
P
e
(
n
)
=
n
ϵ
n
{\displaystyle H(W|{\hat {W}})\leq 1+nRP_{e}^{(n)}=n\epsilon _{n}}
ϵ
n
→
0
{\displaystyle \epsilon _{n}\rightarrow 0}
P
e
(
n
)
→
0
{\displaystyle P_{e}^{(n)}\rightarrow 0}
X
i
{\displaystyle X_{i}}
n
R
=
H
(
W
)
=
I
(
W
;
W
^
)
+
H
(
W
|
W
^
)
≤
I
(
W
;
W
^
)
+
n
ϵ
n
≤
I
(
X
(
n
)
;
Y
(
n
)
)
+
n
ϵ
n
=
h
(
Y
(
n
)
)
−
h
(
Y
(
n
)
|
X
(
n
)
)
+
n
ϵ
n
=
h
(
Y
(
n
)
)
−
h
(
Z
(
n
)
)
+
n
ϵ
n
≤
∑
i
=
1
n
h
(
Y
i
)
−
h
(
Z
(
n
)
)
+
n
ϵ
n
≤
∑
i
=
1
n
I
(
X
i
;
Y
i
)
+
n
ϵ
n
{\displaystyle {\begin{aligned}nR&=H(W)\\&=I(W;{\hat {W}})+H(W|{\hat {W}})\\&\leq I(W;{\hat {W}})+n\epsilon _{n}\\&\leq I(X^{(n)};Y^{(n)})+n\epsilon _{n}\\&=h(Y^{(n)})-h(Y^{(n)}|X^{(n)})+n\epsilon _{n}\\&=h(Y^{(n)})-h(Z^{(n)})+n\epsilon _{n}\\&\leq \sum _{i=1}^{n}h(Y_{i})-h(Z^{(n)})+n\epsilon _{n}\\&\leq \sum _{i=1}^{n}I(X_{i};Y_{i})+n\epsilon _{n}\end{aligned}}}
P
i
{\displaystyle P_{i}}
P
i
=
1
2
n
R
∑
w
x
i
2
(
w
)
{\displaystyle P_{i}={\frac {1}{2^{nR}}}\sum _{w}x_{i}^{2}(w)\,\!}
ここで合計は全ての入力メッセージ
w
{\displaystyle w}
X
i
{\displaystyle X_{i}}
Z
i
{\displaystyle Z_{i}}
Y
i
{\displaystyle Y_{i}}
N
{\displaystyle N}
E
(
Y
i
2
)
=
P
i
+
N
{\displaystyle E(Y_{i}^{2})=P_{i}+N\,\!}
そして、もし
Y
i
{\displaystyle Y_{i}}
h
(
Y
i
)
≤
1
2
log
2
π
e
(
P
i
+
N
)
{\displaystyle h(Y_{i})\leq {\frac {1}{2}}\log {2\pi e}(P_{i}+N)\,\!}
よって
n
R
≤
∑
(
h
(
Y
i
)
−
h
(
Z
i
)
)
+
n
ϵ
n
≤
∑
(
1
2
log
(
2
π
e
(
P
i
+
N
)
)
−
1
2
log
(
2
π
e
N
)
)
+
n
ϵ
n
=
∑
1
2
log
(
1
+
P
i
N
)
+
n
ϵ
n
{\displaystyle {\begin{aligned}nR&\leq \sum (h(Y_{i})-h(Z_{i}))+n\epsilon _{n}\\&\leq \sum \left({\frac {1}{2}}\log(2\pi e(P_{i}+N))-{\frac {1}{2}}\log(2\pi eN)\right)+n\epsilon _{n}\\&=\sum {\frac {1}{2}}\log(1+{\frac {P_{i}}{N}})+n\epsilon _{n}\end{aligned}}}
x の凹(下向き)関数である
log
(
1
+
x
)
{\displaystyle \log(1+x)}
1
n
∑
i
=
1
n
1
2
log
(
1
+
P
i
N
)
≤
1
2
log
(
1
+
1
n
∑
i
=
1
n
P
i
N
)
{\displaystyle {\frac {1}{n}}\sum _{i=1}^{n}{\frac {1}{2}}\log \left(1+{\frac {P_{i}}{N}}\right)\leq {\frac {1}{2}}\log \left(1+{\frac {1}{n}}\sum _{i=1}^{n}{\frac {P_{i}}{N}}\right)\,\!}
各コード名はそれぞれパワー制約を満たすため、平均もパワー制約を満たす。
上の不等式を簡単にすると、
1
2
log
(
1
+
1
n
∑
i
=
1
n
P
i
N
)
≤
1
2
log
(
1
+
P
N
)
{\displaystyle {\frac {1}{2}}\log \left(1+{\frac {1}{n}}\sum _{i=1}^{n}{\frac {P_{i}}{N}}\right)\leq {\frac {1}{2}}\log \left(1+{\frac {P}{N}}\right)\,\!}
よって、全体を合わせると
R
≤
1
2
log
(
1
+
P
N
)
+
ϵ
n
{\displaystyle R\leq {\frac {1}{2}}\log \left(1+{\frac {P}{N}}\right)+\epsilon _{n}}
R
{\displaystyle R}
ϵ
n
→
0
{\displaystyle \epsilon _{n}\rightarrow 0}
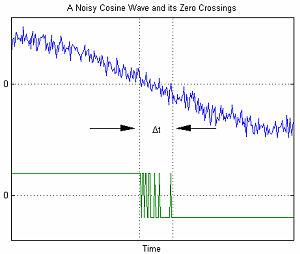
雑音余弦のゼロ交差 シリアルデータ通信においては、ランダムジッタ (RJ)に起因するタイミング誤差をモデル化するためにAWGNの数学モデルが使われる。
右のグラフは、AWGNに関連したタイミングエラーの一例を示している。変数Δtはゼロ交差における不確実性を表す。AWGNの振幅が増加するにつれ、SN比 が減少する。結果として不確実性Δtが増加する[ 1]
AWGNの影響を受けると、入力が正弦波で出力が狭帯域フィルタによる出力である、正もしくは負の方向へ進むゼロ交差の平均回数は以下のようになる。
p
o
s
i
t
i
v
e
z
e
r
o
c
r
o
s
s
i
n
g
s
s
e
c
o
n
d
=
n
e
g
a
t
i
v
e
z
e
r
o
c
r
o
s
s
i
n
g
s
s
e
c
o
n
d
{\displaystyle {\frac {\mathrm {positive\ zero\ crossings} }{\mathrm {second} }}={\frac {\mathrm {negative\ zero\ crossings} }{\mathrm {second} }}}
=
f
0
S
N
R
+
1
+
B
2
12
f
0
2
S
N
R
+
1
{\displaystyle =f_{0}{\sqrt {\frac {\mathrm {SNR} +1+{\frac {B^{2}}{12f_{0}^{2}}}}{\mathrm {SNR} +1}}}}
このとき
f0 はフィルタの中心周波数
Bはフィルタの帯域幅
SNRは線形項における信号対雑音電力比 フェーザ領域におけるAWGNの寄与 現代の通信システムでは、帯域制限されたAWGNは無視できない。フェーザ 領域で帯域制限されたAWGNをモデル化すると、統計的解析により、実部および虚部の振幅はガウス分布 モデルに従う独立変数であることが分かる。これらを結びつけると、合成したフェーザの位相は0から2πまで均一に分布している一方、大きさはレイリー分布 のランダム変数である。
右のグラフは、帯域制限されたAWGNがコヒーレントキャリア信号にどのように影響するかの一例を示している。ノイズベクトルの瞬時応答は正確に予測することはできないが、時間平均応答は統計的に予測することができる。グラフに示されている通り、我々はノイズフェーザの約38%は1σ円内に存在することを確信をもって予測することができる。約86%は2σ円内、約98%は3σ円内に存在する[ 1]
^ a b McClaning, Kevin, Radio Receiver Design , Noble Publishing Corporation