不変質量

不変質量（ふへんしつりょう、英: invariant mass）は、ローレンツ変換によって関連付けられた全ての基準系で不変になるような、系の固有の質量である。不変質量は、系が全体として静止しているときの、系の全エネルギーを光速の二乗で割った値と等しい。

静止質量（せいししつりょう、rest mass）、固有質量（こゆうしつりょう、proper mass）、内在質量（ないざいしつりょう、intrinsic mass）、または単に質量 (mass) とも言う。

概要

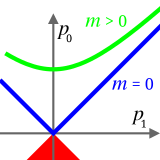
単一または複数の物体で構成される系の不変質量は、系の全エネルギーおよび運動量の性質と関係している。不変質量は、あるスケールで計測される系の質量と等しい。

孤立した系の質量中心が安定した速度で直線上を運動するとき、観測者は常にそれに沿って運動することができる。これは、系の全運動量がゼロになる運動量中心系（ゼロ運動量系）である。このような系は、（気体の入った瓶のような）境界のある系であるなら、全体として"静止している"ようにみなすことができる。不変質量は静止系の全エネルギーをc²で割った値に等しい。ここで、cは光速である。これを質量とエネルギーの等価性と言う。運動量中心系の全エネルギーは、さまざまな慣性系からさまざまな観測者によって観測される中で最小のエネルギーである。この時のエネルギーを静止エネルギーと言う。

二つ以上の粒子で構成された系では、運動量中心系の中で粒子はそれぞれ運動し、基本的な力により相互作用しあう。このとき、粒子の運動エネルギーおよびポテンシャルエネルギーの全エネルギーは粒子の静止質量の和より大きくなり、系の不変質量に寄与する。観測者によって計算される粒子の運動エネルギーの和は、運動量中心系（または、系が境界を持つ場合は静止系）で最小である。

粒子物理

素粒子物理学において、不変質量 $m_{0}$ はエネルギーEおよび運動量pの数学的組み合わせである。この不変質量は全ての基準系において等しく、粒子の静止系における質量の値である。（特殊相対性理論を参照。）不変質量と、光速 $c$ 、エネルギーおよび運動量との関係は次のとおりである：

(m_{0}c^{2})^{2}=E^{2}-c^{2}|{\boldsymbol {p}}|^{2}

または、c = 1である自然単位系においては次のとおりである：

m_{0}^{2}=E^{2}-|{\boldsymbol {p}}|^{2}.

この方程式は、不変質量は4元ベクトル (E, p) の擬ユークリッド長さであることを意味する。空間と時間の次元がそれぞれ逆符号の相対性理論版のピタゴラスの定理を用いて計算される。この長さは四次元でのローレンツブーストや回転に対して保存する。これは、ベクトルの長さが回転に対して保存することと同様である。

不変質量は崩壊反応の期間に保存する量から決定されるので、ある単一粒子の崩壊生成物のエネルギーおよび運動量から計算される不変質量は崩壊した粒子の質量に等しい。粒子系の不変質量は、次の一般的な公式で計算することができる：

\left(Wc^{2}\right)^{2}=\left(\sum E\right)^{2}-c^{2}\left|\sum {\boldsymbol {p}}\right|^{2}

ここで、

W

は、粒子の不変質量である。これは、崩壊粒子の質量に等しい。

\sum E

は、粒子のエネルギーの総和である。

\sum {\boldsymbol {p}}

は、粒子の運動量のベクトル和である。（運動量の大きさと方向を含む。）

不変質量という語は、非弾性散乱実験においても用いられる。反応に使われたエネルギーが検出されたエネルギーより大きい非弾性反応（例えば、生じる全ての粒子がその実験で検出される訳ではない場合）を考えると、反応の不変質量 $W$ （"欠損質量"としても知られる）は次のように定義される：

W^{2}=\left(\sum E_{\text{in}}-\sum E_{\text{out}}\right)^{2}-\left(\sum {\boldsymbol {p}}_{\text{in}}-\sum {\boldsymbol {p}}_{\text{out}}\right)^{2}

系の中で優勢な粒子が実験によって検出されなかった場合、不変質量のプロットは失われた粒子の不変質量の点で大きくピークを描く。

ある方向に沿った運動量は測定することができないような場合、横質量が使われる。例えば、ニュートリノの存在は欠損エネルギーからのみ推測される。

二粒子衝突の例

二粒子衝突（または、二粒子崩壊）における不変質量の二乗は（自然単位系では）次のとおりである：

M^{2}=(E_{1}+E_{2})^{2}-|{\boldsymbol {p}}_{1}+{\boldsymbol {p}}_{2}|^{2}=m_{1}^{2}+m_{2}^{2}+2\left(E_{1}E_{2}-{\boldsymbol {p}}_{1}\cdot {\boldsymbol {p}}_{2}\right).

静止エネルギー

静止エネルギー (rest energy) $E_{0}$ は次のように定義される:

E_{0}=m_{0}c^{2}

,

ここで、 $c$ は真空中の光速である^[1]。一般的に、エネルギーの違いのみが物理的意義を持つ^[2]。

静止エネルギーの概念は、アインシュタインが有名なエネルギーと質量の等価性を導くきっかけとなった特殊相対性理論から得られる。E=mc2も参照のこと。

脚注

[脚注の使い方]

^ http://www.prod.sandia.gov/cgi-bin/techlib/access-control.pl/2006/066063.pdf
^ Modell, Michael; Robert C. Reid (1974). Thermodynamics and Its Applications. Englewood Cliffs, NJ: Prentice-Hall. ISBN 0-13-914861-2

参考文献

Landau, L.D., Lifshitz, E.M. (1975). The Classical Theory of Fields: 4-th revised English Edition: Course of Theoretical Physics Vol. 2. Butterworth Heinemann. ISBN 0-7506-2768-9
Okun, L.B. (1989). The Concept of Mass. http://www.worldscibooks.com/etextbook/6833/6833_02.pdf
Halzen, Francis; Martin, Alan (1984). Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2

概要

粒子物理

二粒子衝突の例

静止エネルギー

脚注

参考文献

関連項目