この項目では、数学用語について説明しています。天文学における等時曲線については「等年齢線 」をご覧ください。
この項目「
等時曲線 」は翻訳されたばかりのものです。不自然あるいは曖昧な表現などが含まれる可能性があり、このままでは読みづらいかもしれません。(原文:
Tautochrone curve )
修正、加筆に協力し、現在の表現をより自然な表現にして下さる方を求めています。
ノートページ や
履歴 も参照してください。
(2017年5月 )
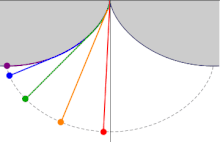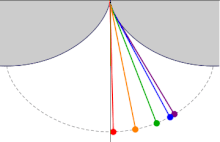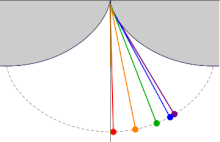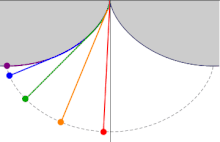
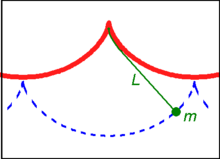
トートクロンカーブを表すオブジェクト サイクロイド曲線を異なる地点から出発して滑り降りる4つの質点は同時に最下点へ到達する。青い矢印は曲線に沿った質点の加速度を示す。右上には時間-位置グラフを示す。 等時曲線 (とうじきょくせん)または等時降下曲線 (とうじこうかきょくせん)とは、物体が一様重力 場の下でその曲線に沿って摩擦 なく滑り降りるとき、最下点に達するまでの時間が出発点に依存しなくなるような曲線 をいう。英語 では tautochrone isochrone curve ギリシャ語 の接頭辞 tauto- iso- chrono- サイクロイド であり、また降下時間はサイクロイドの動円の半径 を重力加速度 で除 したものの平方根 に π 乗 じたものとなる。また、等時曲線は全ての出発点について最速降下曲線 と同一である。
等時曲線問題とは、等時曲線がどのような曲線であるかを同定する問題である。この問題は1659年 にクリスティアーン・ホイヘンス によって解かれた。彼は1673年 初出の自著 Horologium Oscillatorium (英語版 ) サイクロイド であることを幾何学的に証明している。
軸を鉛直とし、頂点を最下点としたサイクロイドの降下時間、すなわち物体が最下点に到達するまでの時間は、サイクロイド上のどの点から出発したとしても互いに等しい...[ 1] ホイヘンスは同時に、降下時間は物体がサイクロイドの動円半径と等しい距離を自由落下するのにかかる時間に π /2r を動円半径、g を重力加速度として π √ r /g
振幅の異なる5つの等時サイクロイド振り子 その後、この解は最速降下曲線 問題への取り組みに活用された。 ヤコブ・ベルヌーイ は最速降下曲線問題を解析学を用いて解き、初めて積分 の用語が用いられた論文 (Acta Eruditorum (英語版 ) [ 2]
サイクロイド振り子の図 ホイヘンスが等時曲線問題を詳しく研究する過程で、円軌道を描く振り子は厳密には等時性 をもっておらず、したがって当時の振り子時計 は振幅によって異なる時間を刻むことが明らかになった。正しい軌道を得たホイヘンスは、おもりを糸で吊し、糸の最上点の傍に障害物を設置しておもりに等時曲線を描かせることを試みた。これらの試みは多くの理由から実用的でなかった。まず、糸が曲がることにより摩擦が生じる。さらに、等時曲線から外れることよりも大きな誤差要因はいくつもあり、あまり改善に役立たない。その上、振り子の「円軌道誤差」は振幅が小さくなるにつれて減少するため、脱進機 (英語版 )
その後、ジョゼフ=ルイ・ラグランジュ とレオンハルト・オイラー がこの問題を解析的に解いた。
質点の位置を最下点からの弧長 s (t )· s 2 y (s )単純調和振動子 のものとなる条件、すなわち、高さが弧長の2乗に等しい時である。長さの単位を比例係数を1となるようにとると
y
(
s
)
=
s
2
{\displaystyle y(s)=s^{2}}
と書ける。この関係を微分形式で書き下し、媒介変数を消去すると以下を得る。
d
y
=
2
s
d
s
{\displaystyle \mathrm {d} y=2s\,\mathrm {d} s}
d
y
2
=
4
s
2
d
s
2
=
4
y
(
d
x
2
+
d
y
2
)
{\displaystyle \mathrm {d} y^{2}=4s^{2}\,\mathrm {d} s^{2}=4y\,(\mathrm {d} x^{2}+\mathrm {d} y^{2})}
これを解くため、 x y
d
x
d
y
=
1
−
4
y
2
y
{\displaystyle {\mathrm {d} x \over \mathrm {d} y}={{\sqrt {1-4y}} \over 2{\sqrt {y}}}}
x
=
∫
1
−
4
u
2
d
u
{\displaystyle x=\int {\sqrt {1-4u^{2}}}\,\mathrm {d} u}
ここで、
u
=
y
{\displaystyle u={\sqrt {y}}}
三角形 と扇形 に切り分けられる。
x
=
1
2
u
1
−
4
u
2
+
1
4
arcsin
2
u
{\displaystyle x={\frac {1}{2}}u{\sqrt {1-4u^{2}}}+{\frac {1}{4}}\arcsin 2u}
y
=
u
2
{\displaystyle y=u^{2}}
これが見慣れない媒介変数表示のサイクロイドであることを示すため、θ = arcsin 2u
8
x
=
2
sin
θ
cos
θ
+
2
θ
=
sin
2
θ
+
2
θ
{\displaystyle 8x=2\sin \theta \cos \theta +2\theta =\sin 2\theta +2\theta }
8
y
=
2
sin
2
θ
=
1
−
cos
2
θ
{\displaystyle 8y=2\sin ^{2}\theta =1-\cos 2\theta }
これは、係数を除いてサイクロイド曲線の通常の媒介変数表示となっている。
等時曲線問題の最も単純な解は、傾斜角とその傾斜角で質点が感じる重力の関係式を直接書き下すものである。傾斜角 90° の鉛直線上の質点は重力の影響を完全に受け、水平線上の質点は重力の影響を全く受けない。中間の傾斜角では質点の感じる「仮想重力」 g sin θ
等時降下を実現するのに必要な「仮想重力」は、残りの距離に単純に比例するものであるから、以下を得る。
d
2
s
d
t
2
=
−
k
2
s
{\displaystyle {\frac {\mathrm {d} ^{2}s}{{\mathrm {d} t}^{2}}}=-k^{2}s}
s
=
A
cos
k
t
{\displaystyle s=A\cos kt}
下式が上の微分方程式の解になっていることは容易に確かめられる。また、どんな高さ A からも時間 π k )s = 0
g
sin
θ
=
−
k
2
s
{\displaystyle g\sin \theta =-k^{2}s\,}
残り距離を明示的に表現するのは困難だが、微分 することにより問題を単純化できる。
g
cos
θ
d
θ
=
−
k
2
d
s
{\displaystyle g\cos \theta \,\mathrm {d} \theta =-k^{2}\,\mathrm {d} s}
d
s
=
−
g
k
2
cos
θ
d
θ
{\displaystyle \mathrm {d} s=-{\frac {g}{k^{2}}}\cos \theta \,\mathrm {d} \theta }
この方程式は曲線の傾斜角の変化と曲線に沿った距離の変化とを関係づけている。ここでピタゴラスの定理 と曲線の傾斜は傾斜角の正接 に等しいことおよび三角 恒等式をいくつか用いると、ds を dx を用いて表現することができる。
d
s
2
=
d
x
2
+
d
y
2
=
(
1
+
(
d
y
d
x
)
2
)
d
x
2
=
(
1
+
tan
2
θ
)
d
x
2
=
sec
2
θ
d
x
2
d
s
=
sec
θ
d
x
{\displaystyle {\begin{aligned}\mathrm {d} s^{2}&=\mathrm {d} x^{2}+\mathrm {d} y^{2}\\\ &=\left(1+\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}\right)\,\mathrm {d} x^{2}\\\ &=(1+\tan ^{2}\theta )\,\mathrm {d} x^{2}\\\ &=\sec ^{2}\theta \,\mathrm {d} x^{2}\\\mathrm {d} s&=\sec \theta \,\mathrm {d} x\end{aligned}}}
これに最初の微分方程式を代入すると、x を θ について解くことができる。
d
s
=
−
g
k
2
cos
θ
d
θ
sec
θ
d
x
=
−
g
k
2
cos
θ
d
θ
d
x
=
−
g
k
2
cos
2
θ
d
θ
=
−
g
2
k
2
(
cos
2
θ
+
1
)
d
θ
x
=
−
g
4
k
2
(
sin
2
θ
+
2
θ
)
+
C
x
{\displaystyle {\begin{aligned}\mathrm {d} s&=-{\frac {g}{k^{2}}}\cos \theta \,\mathrm {d} \theta \\\sec \theta \,\mathrm {d} x&=-{\frac {g}{k^{2}}}\cos \theta \,\mathrm {d} \theta \\\mathrm {d} x&=-{\frac {g}{k^{2}}}\cos ^{2}\theta \,\mathrm {d} \theta \\&=-{\frac {g}{2k^{2}}}\left(\cos 2\theta +1\right)\,\mathrm {d} \theta \\x&=-{\frac {g}{4k^{2}}}\left(\sin 2\theta +2\theta \right)+C_{x}\end{aligned}}}
同様に、dx を dy で表わし、y を θ について解くことができる。
d
y
d
x
=
tan
θ
d
x
=
cot
θ
d
y
cot
θ
d
y
=
−
g
k
2
cos
2
θ
d
θ
d
y
=
−
g
k
2
sin
θ
cos
θ
d
θ
=
−
g
2
k
2
sin
2
θ
d
θ
y
=
g
4
k
2
cos
2
θ
+
C
y
{\displaystyle {\begin{aligned}{\frac {\mathrm {d} y}{\mathrm {d} x}}&=\tan \theta \\\mathrm {d} x&=\cot \theta \,\mathrm {d} y\\\cot \theta \mathrm {d} y&=-{\frac {g}{k^{2}}}\cos ^{2}\theta \,\mathrm {d} \theta \\\mathrm {d} y&=-{\frac {g}{k^{2}}}\sin \theta \cos \theta \,\mathrm {d} \theta \\&=-{\frac {g}{2k^{2}}}\sin 2\theta \,\mathrm {d} \theta \\y&={\frac {g}{4k^{2}}}\cos 2\theta +C_{y}\end{aligned}}}
φ = −2θ r = g /4k 2 x および y についての方程式は水平線を転がる円上の一点の軌跡、すなわちサイクロイド であることがわかる。
x
=
r
(
sin
ϕ
+
ϕ
)
+
C
x
y
=
r
(
cos
ϕ
)
+
C
y
{\displaystyle {\begin{aligned}x&=r(\sin \phi +\phi )+C_{x}\\y&=r(\cos \phi )+C_{y}\end{aligned}}}
k を解き、降下時間が T = π /2k r で表わすことができる。
r
=
g
4
k
2
k
=
1
2
g
r
T
=
π
r
g
{\displaystyle {\begin{aligned}r&={\frac {g}{4k^{2}}}\\k&={\frac {1}{2}}{\sqrt {\frac {g}{r}}}\\T&=\pi {\sqrt {\frac {r}{g}}}\end{aligned}}}
(おおよそ Proctor (1878 , pp. 135–, 139) に基く)
ニールス・アーベル は一般化された等時曲線問題(アーベルの力学問題)、すなわちある関数 T (y )T (y )
アーベルの解は、エネルギー保存 の原理を基礎とする。質点は摩擦を受けないので熱 として失われるエネルギーはなく、運動エネルギー と位置エネルギー の和はつねに出発点における位置エネルギーに等しい。運動エネルギーは 1 / 2 mv 2 ds / dt s は曲線に沿って測った距離である。同様に、初期高さ y 0 y まで落ちたときの重力による位置エネルギーの増加は mg (y 0 − y )
1
2
m
(
d
s
d
t
)
2
=
m
g
(
y
0
−
y
)
d
s
d
t
=
±
2
g
(
y
0
−
y
)
d
t
=
±
d
s
2
g
(
y
0
−
y
)
d
t
=
−
1
2
g
(
y
0
−
y
)
d
s
d
y
d
y
{\displaystyle {\begin{aligned}{\frac {1}{2}}m\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}&=mg(y_{0}-y)\\{\frac {\mathrm {d} s}{\mathrm {d} t}}&=\pm {\sqrt {2g(y_{0}-y)}}\\\mathrm {d} t&=\pm {\frac {\mathrm {d} s}{\sqrt {2g(y_{0}-y)}}}\\\mathrm {d} t&=-{\frac {1}{\sqrt {2g(y_{0}-y)}}}{\frac {\mathrm {d} s}{\mathrm {d} y}}\,\mathrm {d} y\end{aligned}}}
最後の等式において、曲線に沿った残り距離は単調減少し(よって複号は負)、また高さの関数として表わせる (s (y )連鎖律
d
s
=
d
s
d
y
d
y
{\displaystyle \mathrm {d} s={\frac {\mathrm {d} s}{\mathrm {d} y}}\mathrm {d} y}
ここで、y = y 0 y = 0
T
(
y
0
)
=
∫
y
=
y
0
y
=
0
d
t
=
1
2
g
∫
0
y
0
1
y
0
−
y
d
s
d
y
d
y
{\displaystyle T(y_{0})=\int _{y=y_{0}}^{y=0}\,\mathrm {d} t={\frac {1}{\sqrt {2g}}}\int _{0}^{y_{0}}{\frac {1}{\sqrt {y_{0}-y}}}{\frac {\mathrm {d} s}{\mathrm {d} y}}\,\mathrm {d} y}
これをアーベルの積分方程式 と呼ぶ。これにより、曲線が与えられれば(かつ ds / dy T (y 0 )ds / dy ds / dy 1 / √ y 畳み込み とみなし、両辺をラプラス変換 する。
L
[
T
(
y
0
)
]
=
1
2
g
L
[
1
y
]
L
[
d
s
d
y
]
{\displaystyle {\mathcal {L}}[T(y_{0})]={\frac {1}{\sqrt {2g}}}{\mathcal {L}}\left[{\frac {1}{\sqrt {y}}}\right]{\mathcal {L}}\left[{\frac {\mathrm {d} s}{\mathrm {d} y}}\right]}
L
[
1
y
]
=
π
z
−
1
2
{\displaystyle {\mathcal {L}}\left[{\frac {1}{\sqrt {y}}}\right]={\sqrt {\pi }}z^{-{\frac {1}{2}}}}
ds / dy T (y 0 )
L
[
d
s
d
y
]
=
2
g
π
z
1
2
L
[
T
(
y
0
)
]
{\displaystyle {\mathcal {L}}\left[{\frac {\mathrm {d} s}{\mathrm {d} y}}\right]={\sqrt {\frac {2g}{\pi }}}z^{\frac {1}{2}}{\mathcal {L}}[T(y_{0})]}
一般の T (y 0 )T (y 0 )ds / dy ds / dy
等時曲線問題では、T (y 0 ) = T 0 1 のラプラス変換は 1/z であるから、次を得る。
L
[
d
s
d
y
]
=
2
g
π
z
1
2
L
[
T
0
]
=
2
g
π
T
0
z
−
1
2
{\displaystyle {\begin{aligned}{\mathcal {L}}\left[{\frac {\mathrm {d} s}{\mathrm {d} y}}\right]&={\sqrt {\frac {2g}{\pi }}}z^{\frac {1}{2}}{\mathcal {L}}[T_{0}]\\&={\sqrt {\frac {2g}{\pi }}}T_{0}z^{-{\frac {1}{2}}}\end{aligned}}}
上述のラプラス変換を逆に利用することにより、次の結論を得る。
d
s
d
y
=
T
0
2
g
π
1
y
{\displaystyle {\frac {\mathrm {d} s}{\mathrm {d} y}}=T_{0}{\frac {\sqrt {2g}}{\pi }}{\frac {1}{\sqrt {y}}}}
サイクロイドがこの式に従うことは示すことができる。
(Simmons 1972 , Section 54)
^ Blackwell, Richard J. (1986). Christiaan Huygens' The Pendulum Clock . Ames, Iowa: Iowa State University Press. ISBN 0-8138-0933-9 ^ Jeff Miller (20 July 2010). “Earliest Known Uses of Some of the Words of Mathematics (I) ”. 28 June 2012 閲覧。


























![{\displaystyle {\mathcal {L}}[T(y_{0})]={\frac {1}{\sqrt {2g}}}{\mathcal {L}}\left[{\frac {1}{\sqrt {y}}}\right]{\mathcal {L}}\left[{\frac {\mathrm {d} s}{\mathrm {d} y}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5be2d6dc7a016fb628375801ec7033e248789a99)
![{\displaystyle {\mathcal {L}}\left[{\frac {1}{\sqrt {y}}}\right]={\sqrt {\pi }}z^{-{\frac {1}{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae94127504fae1ab4a35206a53bfd2d9637587bf)
![{\displaystyle {\mathcal {L}}\left[{\frac {\mathrm {d} s}{\mathrm {d} y}}\right]={\sqrt {\frac {2g}{\pi }}}z^{\frac {1}{2}}{\mathcal {L}}[T(y_{0})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9643ff791a47b419420abe64789c94230607061)
![{\displaystyle {\begin{aligned}{\mathcal {L}}\left[{\frac {\mathrm {d} s}{\mathrm {d} y}}\right]&={\sqrt {\frac {2g}{\pi }}}z^{\frac {1}{2}}{\mathcal {L}}[T_{0}]\\&={\sqrt {\frac {2g}{\pi }}}T_{0}z^{-{\frac {1}{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a786cd66404e6c83ff234df167ecc1d67eaf2f7e)
