コンテンツにスキップ

英文维基 | 中文维基 | 日文维基 | 草榴社区

「中国の数学」の版間の差分

出典: フリー百科事典『ウィキペディア（Wikipedia）』
履歴の双方向閲覧
← 古い編集新しい編集 →
削除された内容 追加された内容
ビジュアルウィキテキスト
→宋と元の数学: {{要曖昧さ回避}}貼り付け
Cewbot (会話 | 投稿記録)
ボット
779,797 回編集
31行目: 31行目:
==漢の数学==
==漢の数学==
[[File:九章算術.gif|link=https://en-two.iwiki.icu/wiki/File:%E4%B9%9D%E7%AB%A0%E7%AE%97%E8%A1%93.gif|thumb|『[[九章算術]]』]]
[[File:九章算術.gif|link=https://en-two.iwiki.icu/wiki/File:%E4%B9%9D%E7%AB%A0%E7%AE%97%E8%A1%93.gif|thumb|『[[九章算術]]』]]
[[漢代]]では、数字は10進法体系で発展し、空白がゼロを表す9個の記号から成る算木のセットを算盤上で使う[[籌算]]と呼ばれる計算法が使用された{{R|:03}}。負の数および分数も、当時の偉大な数学テキストの解に組み込まれていた{{R|:12}}。当時の数学テキスト『算数書』と『九章算術』は、加算、減算、乗算、除算などの基本的な算術問題を解くものだった。さらに、それらは[[平方根]]と[[立方根]]を求めるためのプロセスを与え、最終的にそれは二次方程式を解いたり最高で三次式を解くのに適用された{{R|:22}}。どちらのテキストも線形代数、すなわち複数の未知数がある[[線型方程式系|連立方程式]]を解くことに関してかなりの進歩を遂げた<ref name=":32">{{Cite book|title=The Chinese Roots of Linear Alegbra|last=Hart|first=Roger|publisher=John's Hopkins University|year=|isbn=978 0801897559|location=|pages=11-85}}</ref>。両方のテキストで[[円周率]]の値は3に等しいとされている<ref name=":82">{{Cite book|title=Pi: A Source Book|last=Lennart|first=Bergren|year=1997|isbn=978-1-4757-2738-8|location=New York|pages=}}</ref>。しかし、数学者の[[劉キン (学者)|劉キン]]（キンは音＋欠）および[[張衡 (科学者)|張 衡]]（78-139年）は、前世紀の中国人が使っていたよりも正確な円周率の概算を出した{{R|:12}}。
[[漢代]]では、数字は10進法体系で発展し、空白がゼロを表す9個の記号から成る算木のセットを算盤上で使う[[籌算]]と呼ばれる計算法が使用された{{R|:03}}。負の数および分数も、当時の偉大な数学テキストの解に組み込まれていた{{R|:12}}。当時の数学テキスト『算数書』と『九章算術』は、加算、減算、乗算、除算などの基本的な算術問題を解くものだった。さらに、それらは[[平方根]]と[[立方根]]を求めるためのプロセスを与え、最終的にそれは二次方程式を解いたり最高で三次式を解くのに適用された{{R|:22}}。どちらのテキストも線形代数、すなわち複数の未知数がある[[線型方程式系|連立方程式]]を解くことに関してかなりの進歩を遂げた<ref name=":32">{{Cite book|title=The Chinese Roots of Linear Alegbra|last=Hart|first=Roger|publisher=John's Hopkins University|year=|isbn=978 0801897559|location=|pages=11-85}}</ref>。両方のテキストで[[円周率]]の値は3に等しいとされている<ref name=":82">{{Cite book|title=Pi: A Source Book|last=Lennart|first=Bergren|year=1997|isbn=978-1-4757-2738-8|location=New York|pages=}}</ref>。しかし、数学者の[[劉歆|劉キン]]（キンは音＋欠）および[[張衡 (科学者)|張 衡]]（78-139年）は、前世紀の中国人が使っていたよりも正確な円周率の概算を出した{{R|:12}}。


数学は、土地の分割や支払いの分割に関する問題など、当時の実際的な問題を解決するために発展した<ref name=":42">{{Cite journal|last=Lay Yong|first=Lam|date=June 1994|title=Nine Chapters on the Mathematical Art: An Overview|journal=Archive for History of Exact Sciences|volume=47|issue=1|pages=1-51|jstor=41133972|doi=10.1007/BF01881700}}</ref>。中国人は、面積や体積を求める方程式を証明するといった、現代の意味での幾何学や代数に基づく理論的証明には焦点を向けていなかった<ref name=":52">{{Cite journal|last=Siu|first=Man-Keung|date=1993|title=Proof and Pedagogy in Ancient China|journal=Educational Studies in Mathematics|volume=24|issue=4|pages=345-357|jstor=3482649|doi=10.1007/BF01273370}}</ref>。『算数書』と『九章算術』は日常生活で使われたであろう多くの実用例を提供している{{R|:52}}。
数学は、土地の分割や支払いの分割に関する問題など、当時の実際的な問題を解決するために発展した<ref name=":42">{{Cite journal|last=Lay Yong|first=Lam|date=June 1994|title=Nine Chapters on the Mathematical Art: An Overview|journal=Archive for History of Exact Sciences|volume=47|issue=1|pages=1-51|jstor=41133972|doi=10.1007/BF01881700}}</ref>。中国人は、面積や体積を求める方程式を証明するといった、現代の意味での幾何学や代数に基づく理論的証明には焦点を向けていなかった<ref name=":52">{{Cite journal|last=Siu|first=Man-Keung|date=1993|title=Proof and Pedagogy in Ancient China|journal=Educational Studies in Mathematics|volume=24|issue=4|pages=345-357|jstor=3482649|doi=10.1007/BF01273370}}</ref>。『算数書』と『九章算術』は日常生活で使われたであろう多くの実用例を提供している{{R|:52}}。
46行目: 46行目:


===円周率の計算===
===円周率の計算===
『九章算術』の問題では、球の表面積など円や球に関連した問題を計算する際に、円周率を3に等しいとしている{{R|:72}}。円周率が3であると計算するための明示公式はテキストに出てこないが、この数値は『九章算術』のほか同時代に作成された『[[周礼#歴史|考工記]]』の問題でも共に使用されている{{R|:82}}。歴史家は、円周率の数値が円周と円の直径の間の（およそ）3：1という関係を用いて計算されたと考えている{{R|:72}}。幾人かの漢代の数学者はこの数値を改善しようと試みており、例えば[[劉キン (学者)|劉キン]]は円周率を3.154と推定したと考えられている{{R|:12}}。彼がこの推定値をどのように計算したかについての明確な方法や記録はない{{R|:12}}。
『九章算術』の問題では、球の表面積など円や球に関連した問題を計算する際に、円周率を3に等しいとしている{{R|:72}}。円周率が3であると計算するための明示公式はテキストに出てこないが、この数値は『九章算術』のほか同時代に作成された『[[周礼#歴史|考工記]]』の問題でも共に使用されている{{R|:82}}。歴史家は、円周率の数値が円周と円の直径の間の（およそ）3：1という関係を用いて計算されたと考えている{{R|:72}}。幾人かの漢代の数学者はこの数値を改善しようと試みており、例えば[[劉歆|劉キン]]は円周率を3.154と推定したと考えられている{{R|:12}}。彼がこの推定値をどのように計算したかについての明確な方法や記録はない{{R|:12}}。


===除法と根の開平法===
===除法と根の開平法===

2020年8月11日 (火) 23:59時点における版

中国の数学（ちゅうごくのすうがく、英:Chinese mathematics）とは、紀元前11世紀までに今の中国で独立して興り、独自に発展した数学のこと[1]。具体的な独自発展には、非常に大きい数および負の数を含む数の設定、十進法、十進法体系の位取り記数法、二進法、代数、幾何学、三角法などがある。

概要

漢代に、中国人は根の展開と線形代数に関してかなりの進歩を遂げた[2]。この時代の主要なテキスト『九章算術』と『算数書』は、日常生活の中で出会う数学的問題を解決するための詳細なプロセスを示している[3]。どちらのテキストでも全ての手順が算盤を用いて計算されており、負の数と分数が含まれている。これらのテキストは、線形代数および二次方程式の解法について、それぞれガウスの消去法およびホーナー法と同様の手順を提示している[4]。西洋ではギリシア数学が中世の間に凋落した一方、中国人の代数の発達は朱世傑が『四元玉鑑』を著した13世紀にその頂点に達した。

『算数書』と『淮南子』はおおむね古典的なギリシア数学と同時代ではあるが、(西洋との）明白な言語的・地理的な障壁や、内容の差異から、中国の数学と古代地中海世界の数学は『九章算術』が最終形に達するまでほぼ独立に発展してきたと考えられている。少なくともローマ時代からは、既知の文化的交流を通じて、アジアをまたいだ思考の交流も若干は行われていた可能性がある。多くの場合、古代社会の数学要素は幾何学や数論といった現代数学の分野で後に見つかる初歩的な結果に対応している。例えば、ピタゴラスの定理は周公旦の時代に証明されている。パスカルの三角形の知識は、宋時代の博学者である沈括など、パスカルよりも数世紀前から中国に存在していたことも示されている[5]。

古代中国の数学

周髀算経における(3, 4, 5)三角形の視覚的な証明。紀元前500-200年
甲骨文字の数字体系
算木で表した十進法

甲骨文字の単純な数学は、殷代（紀元前1600-1050年）まで遡る。現存する最古の数学書物の一つが、周代（紀元前1050-256年）に書かれて多大な影響を与えた『易経』である。数学に関して、この本は六芒星の洗練された使い方を含んでおり、ライプニッツは『易経』に二進法の要素があると指摘した。

殷代以来、中国人はすでに十進法を完全に開発していた。初期の頃から中国人は基本的な四則演算（これは極東の歴史を支配した）、代数、方程式、そして算木を用いることで負の数を理解していた[要出典]。中国人は天文学で使うための算術および高等代数学により焦点を当てていたが、彼らはまた負の数、代数幾何学（中国幾何学のみ）、小数の使用法を開発する先駆けにもなった。

数学は六芸の一つであり、周代の学生はその習得を要求された。 それらを全て完璧に学ぶことが完璧な紳士の嗜みであり、中国で言う「多才多芸」な人に必要とされた。六芸は儒家思想にそのルーツがある。

中国で最古となる幾何学の研究は、墨子（紀元前470-390年）の弟子により編纂された紀元前330年頃の哲学的な正典『墨子』から始まっている。『墨子』は、物理科学に関連した多くの分野のさまざまな側面を説明し、同様に数学に関する小さくも豊富な情報を提供した[注 1]。それは幾何学的な点の「原子的な」定義を提示しており、線がパーツに分けられると、残りのパーツを持たない（要はこれ以上小さく分割できない）部分すなわち線の最端を形成するものが点である、と述べている[7]。ユークリッドの最初と3番目の定義およびプラトンの「線の始まり」と非常によく似ており、『墨子』は「点は出産時における胎児の頭の位置のように（線分の）終わりあるいは始まりにあるかもしれない。（その不可視性に関して）それに類似するものは何もない」と述べている[8]。デモクリトスの原子論者と同様に、『墨子』は点が最小単位であり半分にすることはできない、それ以上は「何もない」から分割できない、と述べた[8]。「長さの比較」や「平行」の定義を提示しながら[9]空間および有界空間の原則とともに[10] 、同じ長さの2線は常に同じ場所で終わると述べた[8]。また、厚さの質がない平面は互いに接触することができないため積み重ねることができないという事実も説明していた[11] 。同書は、体積の定義とともに、円周、直径、半径という単語認識を提示した[12]。

数学的発展の歴史には証拠がいくつか欠落している。特定の数学的古典についてはまだ議論中である。例えば『周髀算経』は紀元前1200-1000年頃とされるが、紀元前300-250年の間に書かれたと確信している学者も多い。『周髀算経』は勾股定理（ピタゴラスの定理の特殊ケース）の徹底的な証明を含んでいるが、より天文計算に集中して掘り下げている。しかし、最近の考古学的発見である清華簡（紀元前305年頃）は、既知の10進法での最初の掛け算九九表など、秦代以前の数学のいくつかの側面を明らかにしている[13]。

そろばんは紀元前2世紀に「算木計算」と並んで最初に言及された。算木計算（籌算)とは、連続した正方形格子に小さな竹棒が配置されるものである[14]。

秦の数学

紀元前213年頃から210年頃に焚書坑儒が起きたため、秦代の数学についてはあまり知られていない。この時期の知識は土木事業や歴史的証拠から判断することが可能である。秦朝は度量衡の基準体系を作りあげた。秦朝の土木事業は人間工学の重要な偉業であった。始皇帝は、他の寺院や神社とともに、宮殿の墓のための大きい等身大の彫像を建てるように多くの男性に命じ、そして墓の形は建築の幾何学的な技能で設計された。人類史上最大の功績の一つ、万里の長城が多くの数学的手法を必要としたことは確かである。秦朝の全ての建物と壮大なプロジェクトでは、体積、面積、比率についての高度な計算式が使用された。

仮報告書によると、香港の古物市場で岳麓書院により購入された秦の竹簡には、数学的論文の最初期の碑文サンプルがあるとのことである[要出典]。

漢の数学

『九章算術』

漢代では、数字は10進法体系で発展し、空白がゼロを表す9個の記号から成る算木のセットを算盤上で使う籌算と呼ばれる計算法が使用された[2]。負の数および分数も、当時の偉大な数学テキストの解に組み込まれていた[3]。当時の数学テキスト『算数書』と『九章算術』は、加算、減算、乗算、除算などの基本的な算術問題を解くものだった。さらに、それらは平方根と立方根を求めるためのプロセスを与え、最終的にそれは二次方程式を解いたり最高で三次式を解くのに適用された[4]。どちらのテキストも線形代数、すなわち複数の未知数がある連立方程式を解くことに関してかなりの進歩を遂げた[15]。両方のテキストで円周率の値は3に等しいとされている[16]。しかし、数学者の劉キン（キンは音＋欠）および張 衡（78-139年）は、前世紀の中国人が使っていたよりも正確な円周率の概算を出した[3]。

数学は、土地の分割や支払いの分割に関する問題など、当時の実際的な問題を解決するために発展した[17]。中国人は、面積や体積を求める方程式を証明するといった、現代の意味での幾何学や代数に基づく理論的証明には焦点を向けていなかった[18]。『算数書』と『九章算術』は日常生活で使われたであろう多くの実用例を提供している[18]。

算数書

『算数書』は190本の竹簡の上に書かれた、長さ約7000字におよぶ数学に関する古代中国のテキストである[19]。それは1984年に考古学者が湖北省の張家山で墓を開いたときに他の著作と一緒に発見された。文書の証拠から、この墓は前漢初期の紀元前186年に封鎖されたことが分かっている[3]。『九章算術』との関連は学者達も議論中だが、一部の内容は明らかにそれと並列している。ただし『算数書』のテキストは『九章算術』に比べて体系的ではなく、複数の情報源から引っ張ってきた文書の、多少なりとも独立した短いセクションでいくつも構成されているようである[19]。

『算数書』には、『九章算術』で拡張されることになる問題に対する多くの補題が含まれる[19]。『算数書』の初等数学の例として、平方根は不足の分子に超過の分母を乗じたものと超過の分子に不足の分母を乗じた値を被除数として組み合わせる、「盈不足（過不足）」方式で近似値を求めさせている[19]。さらに『算数書』は、同じく過不足算を使って、未知数2つの連立方程式を解いている[20][15]。

九章算術

『九章算術』は中国の数学書であり、考古学上は最古で西暦179年[21]（伝統的に紀元前1000年）であるが、恐らく紀元前300-200年に出来たとされる[22]。作者は不明だが、彼らは東洋世界で大きな貢献をした。問題はすぐに答えと手順が続く質問が並んでいる[17]。テキストには正式な数学的証明はなく、段階を追った手順だけである[23]。劉徽の解説は、本文中に示された問題に対する幾何学的証明および代数的証明を提示した[2]。

『九章算術』は中国のあらゆる数学書の中で最も影響を及ぼしたものの1つであり、それは約246の問題で構成されている[22]。それは後の世紀に数学教育の中核となる算経十書に組み込まれることになる[17]。この本には、測量、農産物の交換比例、商品やお金の分配、工学、課税、計算、方程式の解法、および直角三角形の性質に関する246の問題が含まれる[17]。『九章算術』は、二次方程式をホーナー法に似た方法で解くための重要な追加をした[4]。また「防城」あるいは現在の線型代数学として知られているものにも高度な貢献をした[15]。第7章では『算数書』と同様に、過不足算を用いて2つの未知数を含む連立方程式を解いている[15]。第8章では、正と負の数を使用して確定的および不確定な連立一次方程式を解くことを扱い、5つの未知数がある4つの方程式を解く問題がある[15]。『九章算術』は、近代のガウスの消去法および後退代入と同様の方法で連立方程式を解く[15]。

円周率の計算

『九章算術』の問題では、球の表面積など円や球に関連した問題を計算する際に、円周率を3に等しいとしている[22]。円周率が3であると計算するための明示公式はテキストに出てこないが、この数値は『九章算術』のほか同時代に作成された『考工記』の問題でも共に使用されている[16]。歴史家は、円周率の数値が円周と円の直径の間の（およそ）3：1という関係を用いて計算されたと考えている[22]。幾人かの漢代の数学者はこの数値を改善しようと試みており、例えば劉キンは円周率を3.154と推定したと考えられている[3]。彼がこの推定値をどのように計算したかについての明確な方法や記録はない[3]。

除法と根の開平法

加法、減法、乗法、除法といった基本的な四則演算は、漢朝以前に存在していた[3]。『九章算術』は当然ながらこれらの基本演算を扱い、単にそれらを実行するよう読者に指示している[15]。漢代の数学者は除算と同様の方法で平方根と立方根を計算しており、除算と根の開平法に関する問題はいずれも『九章算術』の第4章にある[24]。平方根と立方根の数値計算は、除算と同じように継続的な近似によって行われ、その工程全体で被除数や除数といった同じ用語がよく使用されている[4]。この逐次近似のプロセスは、2次と3次の高次方程式を解くためにホーナー法と同様のやり方でのように拡張された[4]。この手法は漢代でn次の高次方程式を解くために拡張されたものではなかったが、最終的にはこれらの方程式を解くためにこの手法が使われることになる[4]。

算盤での防城

線形代数

『算数書』は、2つの未知数を含む連立方程式を解くための最初の既知のテキストである[15]。『算数書』には過不足算を使って連立方程式を解く問題が3つあり、『九章算術』の7章もまた過不足算を使って2つの未知数がある連立方程式の解法を扱っている[15]。具体的には次のような問いがある。

「鶏を買うのに、各人が9円ずつ出すと11円余り、6円ずつ出すと16円不足する。鶏はいくらで、人数は何人か？」[25]

解き方

壱）出した金額とその過不足をたすき掛けしたものを合計する（不足を負の数とは考えない）。
（9円×不足16円）+（6円×余り11円）= 210
弐）次に、過不足同士を足し算する（不足を負の数とは考えない）。
余り11円 + 不足16円 = 27
参）各人が出した金額について差を求める（これが除数になる）。
各9円 - 各6円 = 3
この時、壱/参（210÷3=70）が鶏の値段。弐/参（27÷3=9）が人数。したがって答えは、鶏70円、人数9人。

続く『九章算術』の8章では無限の未知数を持つ無限方程式の解法を扱っている。この工程は、この章全体を通して「防城手順」と呼ばれている[15]。現在では、多くの歴史家がこの言葉を線形代数と翻訳している。この章では、ガウスの消去法と後退代入の工程を用いて、多くの未知数を含む連立方程式を解いている。問題は算盤上で行われ、負数と分数の使用が含まれていた[15]。算盤は事実上の行列であり、一番上の行が1つの方程式の最初の変数で、一番下の行が最後のものとなる[15]。

劉徽の『九章算術』注釈本

劉徽の取り尽くし法

劉徽の『九章算術』に関する注釈本は、入手可能な原文テキストの最初期の編集本である[22]。劉徽は漢代直後の数学者だと大半の人に信じられている。自身の解説の中で、劉徽は代数的あるいは幾何学的観点からいくつかの問題に条件を付けて証明した[18]。例えば、『九章算術』を通して円や球に関する問題では円周率は3に等しいと見なされている[16]。解説の中で、劉徽は取り尽くし法を用いてより正確な円周率の推定値を見つけた[16]。取り尽くし法では、円の中に内接した多角形を作成して、最終的に高次多角形の面積が円と同じになるよう収束させていく[16]。この方法から、劉徽は円周率の値が約3.14である（これは中国で徽率とも呼ばれる）と主張した[3]。劉徽はまた古代ギリシアの方法と同じに、平方根と立方根の開平法の幾何学的証明を提示した。これは、正方形または立方体を任意の線または断面で切断し、残りの長方形の対称性によって平方根を決定するというものである[24]。

魏晋南北朝時代の数学

劉徽による島の測量
孫武除法のアルゴリズム、西暦400年
アル＝フワーリズミー除法、9世紀
祖沖之の像

3世紀に、劉徽は九章算術の注釈本を著すと、ピタゴラスの定理（九章により既知のもの）および三角測量や四角測量の使用を扱う『海島算経』も執筆した。数学的測量における彼の功績は、西洋で千年かかって到達したものを上回った[26]。彼は自身の円周率演算式（en:Liu Hui's π algorithmを参照）でπ= 3.1416を計算した、最初の中国の数学者である。彼は円柱の体積の正確な公式を見つけるためのカヴァリエリの原理の使用法を発見し、さらに西暦3世紀に微分積分学の要素を開発した。

円周率の分数近似値（補間）

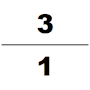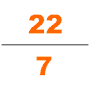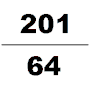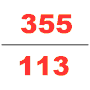
4世紀に、祖沖之という別の有力な数学者が大明暦を導入した。 このカレンダーは、ある期間に起こりうる多くの宇宙論的サイクルを予測するために特別に計算された。彼の人生についてはほとんど知られていない。今日では、唯一の情報源として『隋書』があり、祖沖之が数学者の一人だという事が分かっている。彼は劉徽の円周率演算式（96角形）を使ってそれを1万2288角形に適用し、小数点以下7桁までの正確な円周率の値（3.1415926<π<3.1415927）を得た。これは以後900年にわたって利用可能な最も正確なπの近似値となった。彼はまた自分の天文学と数学の仕事においてこの無理数を分数で近似化するために何承天の調日法を使って、円周率の近似値となる良い分数の密率 を得た。三上義夫は、1585年にオランダの数学者Adrian Anthoniszoomがそれを再発見するまで、ギリシャ人もヒンズー教徒もアラブ人もこの近似分数について知らず、「それゆえ中国人はヨーロッパよりも丸一千年以上早く、全ての小数値の中で最も精緻なものを持っていた」と述べている[27]。

息子の祖コウ（コウは日へん＋恒）と共に、沖之は球の体積を計算する正確な解を見つけるためにカヴァリエリの原理を使った。球の体積の公式に加えて、彼の著書には3次方程式の公式および円周率の精緻な値も掲載されていた。彼の著作『綴術』は宋代に数学摘要から不要とされて散逸した。『綴術』は線形代数、行列代数、πの値を計算するための演算式、球の体積の公式やそれらの手法を含むものだと広く信じられている。このテキストはまた、私達の現代数学と似た知識を含むであろう、彼の天文学的な調日法と関連があるともされている。

西暦200-400年の間に遡る『孫子算経』と呼ばれる算術書は、算木を用いた乗算と除算アルゴリズムの最も詳細な段階的説明を含むものだった。 孫子は位取り記数法とその発展に関与すると共に、関連のある西洋のガレー法 (galley method) に影響を与えた可能性がある。ヨーロッパの研究者達は13世紀に、アル＝フワーリズミーによる9世紀初頭の研究のラテン語翻訳から位取りの技法を学んだ。フワーリズミーの表現は、様式的な点でも孫子の除算アルゴリズムとほぼ同じである（例えば、末尾のゼロを表すために空白を使用するなど）。その類似性は、結果が独立した発見ではなかった可能性を示唆している。フワーリズミーの著作に関するイスラム評論家は、それが主にヒンズー教の知識を要約したと信じていた。アル＝フワーリズミーは自分の情報源を引用しなかったため、それらが中国から順番に手順を学んだかどうかを判断するのは困難である[28]。

5世紀に『張丘建算経』と呼ばれる教本が線形方程式および二次方程式を論じた。 この時点で中国人は負の数という概念を持っていた。

唐の数学

唐代までに数学の勉強は大きな学校ではかなり標準的だった。算経十書は中国の数学著作10冊を集めたもので、唐代初期の数学者である李淳風(602‐670)によって、数学の帝国試験の公式な数学教科書として編纂された。隋王朝と唐王朝は「計算の学校」を運営した[29]。

唐代初頭の偉大な数学者である王孝通は『緝古算経』という本を著し、そこには一般的な三次方程式が初めて現れる[30]。

チベット人は、630年に死去したナムリ・ソンツェン[注 2]の治世中に中国から最初の数学知識を得た[31][32]。

インドの数学者アーリヤバタによる正弦の表は、唐代の西暦718年にまとめられた『開元占経』という中国の数学書に翻訳された[33]。中国人は立体幾何学、二項定理、複雑な代数公式といった数学分野で優れていたが、初期の三角法は同時代のインドやイスラムの数学ほど広く認知されていなかった[34]。

数学者で仏教の僧侶でもある一行は、正接表を計算したとされている。 正弦、正接、正割を使用する平面三角関数の実用的使用が知られてはいたものの、昔の中国人は代わりにチョンチャとして知られる経験的置換を使っていた[33]。一行はその博識が有名で、囲碁ゲームで可能なポジションの数を計算したことでも知られる（ただし、ゼロ記号なしでその数を表すのは困難だった）。

宋と元の数学

朱世傑の四元玉鑑（1303年）に図示された、算木を用いた楊輝の三角形（パスカルの三角形）

宋代の数学者賈憲は、ホーナー法を実行する平方根と立方根の開平のための加法乗法を開発した[35]。

宋と元の時代に、特に12世紀と13世紀に優れた数学者が4人出てきた。楊輝、秦九韶、李冶、朱世傑である。600年前に彼らは全員がホーナー法とルフィニのルールを使って、特定のタイプの連立方程式、根、二次方程式、三次方程式、および四次方程式を解いた。楊輝はまた「パスカルの三角形」を発見して、その二項証明も一緒に証明した最初の人物だった（ただし中国ではパスカルの三角形に関する最初の言及が11世紀以前に存在する）。一方で李冶は天元術に基づいた代数幾何学の形式について調べた。 彼の著書『測円海鏡』は、ピタゴラスの定理を使う従来の方法ではなく、代数によってこの幾何学問題を回すことにより円を三角形に内接するというアイデア革命をもたらした。この時代の郭守敬はまた、正確な天文計算のために球面三角法に取り組んだ。 数学史のこの時点では、現代西洋数学の多くが中国の数学者によってすでに発見されていた。

物事は13世紀の中国の数学復興までしばらく静かになった。ここで中国の数学者が、ヨーロッパでは18世紀まで知られていなかった方法で方程式を解いている様子が見られた。この時代は、朱世傑の2冊の本『算学啓蒙』と『四元玉鑑』で最高点を迎えた。ある時に、彼はガウス[要曖昧さ回避]のピボット（英語版）凝縮と同等の方法を与えたと伝えられている。

秦九韶(1201-1261)は中国の数学にゼロ記号を導入した最初の人物だった[36]。この革新以前は、算木システムでゼロの代わりに空白スペースが使用されていた[37]。秦九韶の最も重要な貢献の1つは、高次方程式を解く彼の方法である。 彼の四次方程式の解を参照して、三上義雄は「輝かしいホーナーの工程が、中国では少なくともヨーロッパより約6世紀早く使用されていたという事実を誰が否認できようか？」と述べている[38]。また秦は10次方程式を解いた[39][注 3]

パスカルの三角形は、中国では楊輝によって著書『祥解九章算法』の中に図示されたが、さらに昔の1100年頃に賈憲によって記述されていた[40] 。朱世傑によって1299年に書かれた『算学啓蒙』は中国の代数に新しいものを何も含んでいなかったが、それは日本の数学の発展に大きな影響を与えた[41]。

代数

李冶による三角形の内接円、『測円海鏡』より

『測円海鏡』

『測円海鏡』は、李冶(1192-1279)によって書かれた、692個の公式と170個の三角形の内接円に関する問題集である。彼は天元術を用いて複雑な幾何問題を純粋な代数問題に変換した。彼はその後ホーナー法を使って6次までの高次方程式を解いた、しかし彼は方程式を解く自らの方法を説明しなかった[42]。李冶は1206年にクビライ・カーンによって政府の官職を提示された北京の数学者だが、丁重にそれを固辞している。彼の『測円海鏡』は、6次の代数方程式に至るいくつかの問題を含む170の問題を取り扱っている。彼は方程式の自分の解法について記述しなかったが、それは朱世傑やホーナーによって使用されたものとさほど違いが無いようである。 ホーナー法を使用した他の者には、朱世傑と楊輝がいた。

『四元玉鑑』

朱世傑の『四元玉鑑』の写し。

『四元玉鑑』は1303年に朱世傑によって書かれ、中国の代数学発展のピークを示している。天、地、人、物と呼ばれる4つの要素は、彼の代数方程式の4つの未知数を表していた。この書物は連立方程式と14次の高次方程式を扱っている。著者はこれらの方程式を解くために現在はホーナー法と呼ばれる手法を使用している[43]。

同書には証明なしに与えられた多くの総和級数式がある。一部の総和級数は次のとおり[44]。

楊輝による同心円魔方陣-それぞれの円と直径は（中心の9は除く）いずれも総和が138になる。

『数書九章』

『数書九章』は、裕福な総督で大臣だった秦九韶によって書かれた。そこには連立合同式を解く方法の発明があり、それは中国の不確定性分析における最高点を示すものである[42]。

魔方陣とその円形陣

3よりも大きな列の知られている最初期の魔方陣は楊輝によるものとされ、彼は10列の魔方陣を作っていた[45]。彼はまた同様の円形陣も作った。

三角法

中国における三角法の未発達状態は、宋代(960-1279)の間にゆっくりと変化して進歩が始まり、そこで中国の数学者は暦科学と天文計算における球面三角法の必要性を主張し始めた[33]。博学者で中国の科学者、数学者、官僚の沈括(1031-1095)は三角関数を使って和音と円弧の数学的問題を解いた[33]。沈括の「交差する円の技法」公式で、彼は円sの円弧の近似を s = c + 2v2/d と算出した（ここでdは直径、vは余弦、cは円弧の範囲内の弦の長さ）とヴィクター・カッツは書いている[46]。サル・レスティボは、13世紀に数学者で天文学者の郭守敬(1231-1316)によって開発された球面三角法の基礎を、円弧の長さに関する沈の研究が提供したと書いている[47] 。歴史学者L. Gauchetとジョゼフ・ニーダムが述べているように、郭守敬は彼の計算に球面三角法を用いて中国の暦体系と天文学を改善した[33][48]。

沈と郭の三角法に関する研究の成果にもかかわらず、中国の三角法に関するもう1つの重要な研究は1607年まで再び発表されることはなく、中国の官吏で天文学者の徐光啓(1562-1633)とイタリアの マテオ・リッチ(1552-1610)による共著『ユークリッド原論』を待つことになる[49]。

明の数学

元王朝の転覆後、中国はモンゴルが好む知識を疑わしく感じるようになった。官吏は数学や物理学を避けるようになり、植物学および薬理学を支持した。科挙にはほとんど数学が含まれておらず、そのことが直近の発展を妨げていた。Martzloffは次のように書いている。

16世紀末に、中国人自身が知っている中国の独自数学はそろばんの計算以上のものがほぼ何もなかった、一方で17世紀と18世紀にヨーロッパ科学の舞台における革命的進歩には比類するものがなかった。さらにこの同時期には、中国人自身が断片的な知識しか持っていなかったため、より遠い過去に起こったことを誰も伝えることができなかった。中国自体としては、18世紀最後の四半世紀以前に大規模な独自発展の数学が再発見されなかったことを忘れるべきではない[50]。

明朝の数学を避ける方針に呼応して、学者らは数学にあまり注意を払わなかった。顧應祥や唐順之などの優れた数学者は天元術を知らなかったようである[51]。それらを口頭説明する対話者がいないことで、そのテキストが急速に理解できなくなってしまった。さらに悪いことに、ほとんどの問題がもっと基本的な方法で解決できた。そのため平均的な学者にとって天元術は数秘術のように思えた。Wu Jingが以前の王朝のすべての数学的作品を『九章算術』注釈本にまとめたとき、彼は天元術と増乗開平法（ホーナー法）を省いてしまった。

中国のそろばん

代わりに、数学的進歩は計算道具に集中するようになった。15世紀に、そろばんは算盤（さんばん）の形状になった。速くて正確、使いやすくて持ち運びが簡単な計算法として、算木を急速に上回った。そろばんによる計算の「珠算」は、複数の新しい作品に影響を与えた。1592年に程大位によって出版された17巻の著作『算法統宗』は、300年以上にわたって使用され続けた[52]。鄭恭王の王子である朱載イク（イクは土へん+育）は、2から25の平方根および立方根を正確に計算するため81桁のそろばんを使用し、この精度が平均律法の開発を可能にした。

算木からそろばんへの切り替えにより計算時間の短縮ができるようになったが、それがまた中国数学の停滞と衰退につながった可能性がある。 算盤上の算木数字のパターン豊富な配置は、分数のたすき掛け原則および線形方程式を解く方法など、数学における多くの中国の発明を刺激した。同様に、日本の数学者たちは行列の概念の定義で算木数字の配置に影響を受けた。そろばんのための演算法は、同様の概念上の進歩にはつながらなかった。

16世紀後半、マテオ・リッチは宮廷における地位を確立するため西洋の科学作品を発表することを決めた。徐光啓の助けを借りて、彼は古典的な仏教テキストを教えるために使うのと同じ技術を使用してユークリッドの『原論』を翻訳することに成功した[53]。彼の前例に続いて、他の宣教師が中国の伝統では無視されていた特別な関数（三角法と対数）に関する西洋の著作を翻訳した[54]。しかしながら、同時代の学者たちは問題を解くのとは対照的に（西洋の著作が）証明に重点を置いていることに気づき、大半の者が古典テキストだけで研究を続けていた[55]。

清代

西洋教育を受けた康熙帝の下で、中国の数学は短期間の公的支援を受けた[56]。康熙の指示で、梅穀成と他の3人の優れた数学者は53巻の『数理精蘊』（1723年印刷）を編集し、それは西洋の数学的知識を体系的に紹介した[57]。同時に、梅穀成はまた『梅氏叢書輯要』（彼の編纂した作品）に取り組んだ。『梅氏叢書輯要』は当時のほぼ全学校の中国数学の百科事典的要約だったが、穀成の祖父である梅文鼎の異文化研究も含んでいた[58][59]。この事業は、西洋数学を研究する中国の数学者にとって引用をたどる際の難しさを軽減しようとするための取り組みだった[60]。

しかし、雍正帝が帝位に就くよりも早くその百科事典が発表されたわけではない。雍正は中国の政策にアンチ西洋方針を厳しく導入し、宮廷からほとんどの宣教師を追放した。西洋のテキストもわかりやすい中国語テキストも利用できないため、中国の数学は停滞した。

1773年、乾隆帝は『四庫全書』を編纂することを決定した。戴震(1724-1777)は永楽大典からの『九章算術』と、唐代および唐代の数学作品をいくつか選び、校正した[61]。『四元玉鑑』『測円海鏡』といった、宋代や元代から失われて久しかった数学的作品も発見されて印刷され、それが新しい研究の波に直接つながった[62]。最も注釈が付けられた作品は、李フアン（フアンは、さんずい+黃）によって寄稿された『九章算術細草図説』および羅士琳による『四元玉鑑細草』であった[63]。

西洋の影響

1840年、阿片戦争が中国に外の世界を知らしめる扉を開けさせることになった。それはまた、以前の世紀とは比べ物にならない速さでの西洋数学の研究流入につながった。1852年、中国数学者の李善蘭とイギリス宣教師のアレクサンダー・ワイリーが、後の9巻の『原論』と13巻の『幾何（原論）』を共同翻訳した[64][65]。

ジョゼフ・エドキンズの助けを借りて、すぐに天文学と微積分学に関するより多くの研究が続いた。中国の学者たちは当初、新しい研究に取り組むべきかどうか迷っており、西洋知識の研究を海外侵略者への服従の形と捉えていた節もあるようである。しかし同世紀末までに、中国は西洋の研究を取り入れて国力増強を図る方針（洋務運動）を明確にした。西洋の宣教学校で西洋の翻訳済みテキストから教えを受けた中国の学者たちは、急速に先住民族の伝統と関与しなくなった。Martzloffが述べているように「1911年以降、西洋数学のみが中国で実践されてきた」のである[66]。

近代中国における西洋数学

近代の1912年に中華民国が設立されて以来、中国の数学は大きな復活を遂げた。それ以来、現代の中国の数学者はさまざまな数学分野で多くの業績を上げている。

著名な現代の中国人数学者には次のような人物がいる。

  • 陳省身は、幾何学のリーダーであり、20世紀の最も偉大な数学者の一人であると広く見なされており、彼の膨大な数の数学的貢献によりウルフ賞を受賞した[67][68]。
  • 樊チー（チーは土へん+畿）は、数学のさまざまな分野に多大な基礎的貢献をした。固定小数点理論における彼の仕事は、非線形関数解析に影響を与えるのみならず、数理経済学、ゲーム理論、ポテンシャル論、変分法、および微分方程式に広く応用されている。
  • シン＝トゥン・ヤウ - 彼の貢献は物理学と数学の両方に影響を与え、幾何学と理論物理学の間の橋渡しで活躍し、後にフィールズ賞を受賞した。
  • テレンス・タオ - 16歳のときに修士号を取得した中国の神童は、国際数学オリンピックの全歴史の中で最も若い参加者で、最初は10歳で競技に参加し、銅メダル、銀メダル、金メダルを獲得した。彼は数学オリンピックの歴史において金銀銅いずれのメダルでも最年少の獲得者となっている。 後にフィールズ賞を受賞した。
  • 張益唐 - 素数間のギャップに関する最初の有限範囲を確立した数論学者。
  • 陳景潤 - 十分大きな偶数は素数 p および高々2つの素数の積である整数 n の和 p + n の形で表せるという陳の定理を証明した数論学者[69]。彼の研究はゴールドバッハ予想の研究における画期的成果として知られている。

国際数学オリンピックでの成果

国際数学オリンピックに参加している他の国々と比較して、中国は最も高いチーム得点を誇り、チームで全員金メダルという成績を最も多く獲得した[70]。

古代中国の数学テキスト

周代

『周髀算経』（紀元前1000-西暦100年頃）

  • 天文学理論と計算技術
  • ピタゴラスの定理の証明
  • 分数計算
  • 天文学的目的でのピタゴラスの定理

『九章算術』（紀元前1000？-西暦50年頃）

  1. 方田 - 四則演算、平面図形の面積
  2. 粟米 - 物々交換の比例算
  3. 衰分 - お金の分配、利息計算
  4. 少広 - 平方根・立方根
  5. 商功 - 体積、円周率を3とする
  6. 均輸 - 租税計算
  7. 盈不足 - 過不足算、復仮定法
  8. 方程 - ガウスの消去法、行列演算
  9. 句股 - ピタゴラスの定理（勾股弦の定理）
漢代

『算数書』（紀元前202-186年）

  • 様々な立体形状の体積の計算
  • 長方形の未知の辺、与えられた面積と一辺の計算
  • 開平するためのはさみうち法の使用と平方根の近似値抽出
  • 異なる単位間の変換

教育における数学

中国における数学学習に使用された書籍への最初の言及は西暦2世紀に遡る（『後漢書』24、862; 35,1207）。馬融(79-166)と鄭玄(127-200)がいずれも『九章算術』を研究したと言われている。数学が医学と同じように口頭で教えられたとC.Cullenは主張している[71]。張家山漢簡からの『算数書』の文体は、テキストが様々な情報源から集められ、それから成文化されたことを示唆している[71]。

脚注

[脚注の使い方]

注釈

  1. ^ 『墨子』53篇では様々な論考がされているが、うち「墨弁」と呼ばれる6篇が、論理学・自然学の概念や命題を論じている[6]。
  2. ^ チベットに初めて仏教を導入したことで知られるソンツェン・ガンポの父親。
  3. ^ 現代では、アーベル-ルフィニの定理から五次以上の代数方程式には解の公式が存在しないことが分かっており、秦九韶はあくまで「答えを導き出せうる」特定の10次方程式を解いたことになる。

出典

  1. ^ Chinese overview
  2. ^ a b c Chemla, Karine. “East Asian Mathematics”. Britannica Online Encyclopedia. 2019年5月11日閲覧。
  3. ^ a b c d e f g h Needham, Joseph (1959). Science and Civilization in China. England: Cambridge University Press. pp. 1-886. ISBN 0 521 05801 5 
  4. ^ a b c d e f Needham, Joseph (1955). “Horner's Method in Chinese Mathematics”. T'oung Pao, Second Series 43 (5): 345-401. JSTOR 4527405. 
  5. ^ Frank J. Swetz and T. I. Kao: Was Pythagoras Chinese?
  6. ^ 日本大百科全書(ニッポニカ)『墨子』 - コトバンク
  7. ^ Needham, Volume 3, 91.
  8. ^ a b c Needham, Volume 3, 92.
  9. ^ Needham, Volume 3, 92-93.
  10. ^ Needham, Volume 3, 93.
  11. ^ Needham, Volume 3, 93-94.
  12. ^ Needham, Volume 3, 94.
  13. ^ Jane Qiu (7 January 2014). “Ancient times table hidden in Chinese bamboo strips”. Nature. doi:10.1038/nature.2014.14482. http://www.nature.com/news/ancient-times-table-hidden-in-chinese-bamboo-strips-1.14482 15 September 2016閲覧。. 
  14. ^ Ifrah, Georges (2001). The Universal History of Computing: From the Abacus to the Quantum Computer. New York, NY: John Wiley & Sons, Inc.. ISBN 978-0471396710 
  15. ^ a b c d e f g h i j k l Hart, Roger. The Chinese Roots of Linear Alegbra. John's Hopkins University. pp. 11-85. ISBN 978 0801897559 
  16. ^ a b c d e Lennart, Bergren (1997). Pi: A Source Book. New York. ISBN 978-1-4757-2738-8 
  17. ^ a b c d Lay Yong, Lam (June 1994). “Nine Chapters on the Mathematical Art: An Overview”. Archive for History of Exact Sciences 47 (1): 1-51. doi:10.1007/BF01881700. JSTOR 41133972. 
  18. ^ a b c Siu, Man-Keung (1993). “Proof and Pedagogy in Ancient China”. Educational Studies in Mathematics 24 (4): 345-357. doi:10.1007/BF01273370. JSTOR 3482649. 
  19. ^ a b c d Dauben, Joseph W. (2008). “算数書 Suan Shu Shu A Book on Numbers and Computations: English Translation with Commentary”. Archive for History of Exact Sciences 62 (2): 91-178. doi:10.1007/s00407-007-0124-1. JSTOR 41134274. 
  20. ^ 城地茂「『算数書』日本語訳」、大阪教育大学『 和 算 研 究 所 紀 要 』4(2001年)、19-46頁。 39頁の「 分銭 」「 米出銭 」「方田」が過不足算を使って解く問題となっている（同資料では、原文に合わせて「盈不足」という昔の用語を使っている）。
  21. ^ 大川俊隆「『九章算術』訳注稿（1）」、大阪産業大学『大阪産業大学論集 人文・社会科学編』2、2007年10月31日（原稿受理）。11頁
  22. ^ a b c d e Dauben, Joseph (2013). “九章算術 "Jiu zhang suan shu" (Nine Chapters on the Art of Mathematics)An Appraisal of the Text, its Editions, and Translations”. Sudhoffs Archiv 97 (2): 199?235. JSTOR 43694474. PMID 24707775. 
  23. ^ Straffin, Philip D. (1998). “Liu Hui and the First Golden Age of Chinese Mathematics”. Mathematics Magazine 71 (3): 163-181. doi:10.2307/2691200. JSTOR 2691200. 
  24. ^ a b Yong, Lam Lay (1970). “The Geometrical Basis of the Ancient Chinese Square-Root Method”. Isis 61 (1): 92-102. doi:10.1086/350581. JSTOR 229151. 
  25. ^ 馬場理惠子「『九章算術』訳注・稿（21）」、大阪産業大学『大阪産業大学論集 人文・社会科学編』25、2015年6月30日原稿受理。22-24頁。
  26. ^ Frank J. Swetz: The Sea Island Mathematical Manual, Surveying and Mathematics in Ancient China 4.2 Chinese Surveying Accomplishments, A Comparative Retrospection p63 The Pennsylvania State University Press, 1992 ISBN 0-271-00799-0
  27. ^ 三上義夫, The Development of Mathematics in China and Japan, chap 7, p. 50, reprint of 1913 edition Chelsea, NY, Library of Congress catalog 61-13497.英文書籍で未邦訳。isbn 0828401497
  28. ^ Lam Lay Yong (1996). “The Development of Hindu Arabic and Traditional Chinese Arithmetic”. Chinese Science 13. オリジナルの2012-03-21時点におけるアーカイブ。. https://web.archive.org/web/20120321111930/http://sciences.aum.edu/~sbrown/Hindu%20Arabic%20and%20Chinese.pdf 2015年12月31日閲覧。. 
  29. ^ Alexander Karp; Gert Schubring (25 January 2014). Handbook on the History of Mathematics Education. Springer Science & Business Media. pp. 59-. ISBN 978-1-4614-9155-2. https://books.google.com/?id=MYy9BAAAQBAJ&pg=PA59&dq=wujing+boshi#v=onepage&q=wujing%20boshi&f=false 
  30. ^ Yoshio Mikami, Mathematics in China and Japan,p53
  31. ^ Hugh Chisholm, ed (1911). The encyclopædia britannica: a dictionary of arts, sciences, literature and general information, Volume 26 (11 ed.). At the University press. p. 926. https://books.google.com/?id=uDQEAAAAYAAJ&pg=PA926&dq=sixth+century+the+tibetans+obtained+their+first+knowledge+of+arithmetic+and+medicine+from+the+chinese#v=onepage&q=sixth%20century%20the%20tibetans%20obtained%20their%20first%20knowledge%20of%20arithmetic%20and%20medicine%20from%20the%20chinese&f=false 2011年7月1日閲覧。 The Encyclopædia Britannica: A Dictionary of Arts, Sciences, Literature and General Information, Hugh Chisholm
  32. ^ Translated by William Woodville Rockhill, Ernst Leumann, Bunyiu Nanjio (1907). The Life of the Buddha and the early history of his order: derived from Tibetan works in the Bkah-hgyur and Bstan-hgyur followed by notices on the early history of Tibet and Khoten. K. Paul, Trench, Tr?bner. p. 211. https://books.google.com/?id=rVXYAAAAMAAJ&pg=PA211&dq=sixth+century+the+tibetans+obtained+their+first+knowledge+of+arithmetic+and+medicine+from+the+chinese#v=onepage&q&f=false 2011年7月1日閲覧。 
  33. ^ a b c d e Needham, Volume 3, 109.
  34. ^ Needham, Volume 3, 108-109.
  35. ^ Martzloff (1987), p. 142.
  36. ^ Needham, Volume 3, 43.
  37. ^ Needham, Volume 3, 62‐63.
  38. ^ Yoshio Mikami, The development of Mathematics in China and Japan, p77 Leipzig, 1912
  39. ^ Ulrich Librecht,Chinese Mathematics in the Thirteenth Century p. 211 Dover 1973
  40. ^ Needham, Volume 3, 134-137.
  41. ^ Needham, Volume 3, 46.
  42. ^ a b (Boyer 1991, "China and India" p. 204)
  43. ^ (Boyer 1991, "China and India" p. 203)
  44. ^ (Boyer 1991, "China and India" p. 205)
  45. ^ (Boyer 1991, "China and India" pp. 204-205) "The same "Horner" device was used by Yang Hui, about whose life almost nothing is known and who work has survived only in part. Among his contributions that are extant are the earliest Chinese magic squares of order greater than three, including two each of orders four through eight and one each of orders nine and ten."
  46. ^ Katz, 308.
  47. ^ Restivo, 32.
  48. ^ Gauchet, 151.
  49. ^ Needham, Volume 3, 110.
  50. ^ Martzloff (1987), p. 4.
  51. ^ He, Ji-Huan (May 2004). “Some interpolation formulas in Chinese ancient mathematics”. Applied Mathematics and Computation 152 (2): 367-371. doi:10.1016/s0096-3003(03)00559-9. ISSN 0096-3003. 
  52. ^ “East Asian Journal on Applied Mathematics”. East Asian Journal on Applied Mathematics. doi:10.4208/eajam. 
  53. ^ Martzloff (1987), p. 21.
  54. ^ Brucker, Joseph (1912). "Matteo Ricci". The Catholic Encyclopedia. New York: Robert Appleton Company. OCLC 174525342. Retrieved 17 August 2017.
  55. ^ Martzloff (1987), p. 29.
  56. ^ Martzloff (1987), pp. 25–8.
  57. ^ Jami, Catherine; Qi, Han (2003-01-01). “The Reconstruction of Imperial Mathematics in China During the Kangxi Reign (1662-1722)”. Early Science and Medicine 8 (2): 88-110. doi:10.1163/157338203X00026. ISSN 1573-3823. 
  58. ^ Jami, Catherine (2011-12-01), A mathematical scholar in Jiangnan: The first half-life of Mei Wending, “The Emperor's New Mathematics Western Learning and Imperial Authority During the Kangxi Reign (1662-1722)”, The Emperor's New MathematicsWestern Learning and Imperial Authority During the Kangxi Reign (1662-1722) (Oxford University Press): pp. 82-101, doi:10.1093/acprof:oso/9780199601400.003.0005, ISBN 9780199601400, http://www.oxfordscholarship.com/view/10.1093/acprof:oso/9780199601400.001.0001/acprof-9780199601400-chapter-5 2018年7月28日閲覧。 
  59. ^ 1946-, Elman, Benjamin A. (2005). On their own terms : science in China, 1550-1900. Cambridge, Mass.: Harvard University Press. ISBN 9780674036475. OCLC 443109938 
  60. ^ Martzloff (1987), p. 28.
  61. ^ Minghui, Hu (2017-02-14). China's transition to modernity : the new classical vision of Dai Zhen. Seattle. ISBN 978-0295741802. OCLC 963736201 
  62. ^ Jean-Claude Martzloff, A History of Chinese Mathematics, Springer 1997 ISBN 3-540-33782-2
  63. ^ Catherine, Jami (2012). The emperor's new mathematics : Western learning and imperial authority during the Kangxi Reign (1662-1722). Oxford: Oxford University Press. ISBN 9780191729218. OCLC 774104121 
  64. ^ Carlyle, Edward Irving (1900). "Wylie, Alexander". In Lee, Sidney. Dictionary of National Biography. 63. London: Smith, Elder & Co.
  65. ^ "Li Shanlan's Summation Formulae". A History of Chinese Mathematics: 341?351. doi:10.1007/978-3-540-33783-6_18.
  66. ^ Martzloff (1987), pp. 34–9.
  67. ^ “Chern biography”. www-history.mcs.st-and.ac.uk. 2017年1月16日閲覧。
  68. ^ “12.06.2004 - Renowned mathematician Shiing-Shen Chern, who revitalized the study of geometry, has died at 93 in Tianjin, China”. www.berkeley.edu. 2017年1月16日閲覧。
  69. ^ J. R., Chen (1973). On the representation of a larger even integer as the sum of a prime and the product of at most two primes. Sci. Sinica 
  70. ^ “Team Results: China at International Mathematical Olympiad”. 2019年5月11日閲覧。
  71. ^ a b Christopher Cullen, "Numbers, numeracy and the cosmos" in Loewe-Nylan, China's Early Empires, 2010:337-8.

参考文献

関連項目

外部リンク

Project:数学
プロジェクト 数学
「https://ja-two.iwiki.icu/w/index.php?title=中国の数学&oldid=78945802」から取得