ラプラシアン行列

グラフ理論の数学的分野において、ラプラシアン行列（ラプラシアンぎょうれつ、英: Laplacian matrix）は、グラフの行列表示（行列表現）である。アドミタンス行列（admittance matrix）、キルヒホッフ行列（Kirchhoff matrix）、離散ラプラシアン（discrete Laplacian）、またはラプラス行列と呼ばれることもある。ラプラシアン行列はグラフの多くの有用な性質を探るために使うことができる。キルヒホッフの定理と一緒に、任意のグラフにつていの全域木の数を計算するために使うことができる。グラフの最疎カットはチーガーの不等式によってそのラプラシアンの2番目に小さい固有値を使って近似することができる 。また、低次元埋め込みを構築するためにも使うことができる。これは、様々な機械学習応用のために有用かもしれない。

定義

単純グラフのラプラシアン行列

n個の頂点を持つ単純グラフを考えると、そのラプラシアン行列${\textstyle L_{n\times n}}$は以下の式で定義される。

$L=D-A$

上式において、Dはグラフの次数行列、Aは隣接行列である。${\textstyle G}$は単純グラフであるため、${\textstyle A}$の成分は1または0のみであり、その対角要素は全て0である。

有向グラフの場合は、入次数または出次数のいずれかが、応用に依存して使われるだろう。

${\textstyle L}$の要素は式

$L_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j\\-1&{\mbox{if}}\ i\neq j\ {\mbox{and}}\ v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}\end{cases}}$

によって与えられる。上式において、$\operatorname {deg} (v_{i})$は頂点$i$の次数である。

対称正規化ラプラシアン

対称正規化ラプラシアン行列は

$L^{\text{sym}}:=D^{-{\frac {1}{2}}}LD^{-{\frac {1}{2}}}=I-D^{-{\frac {1}{2}}}AD^{-{\frac {1}{2}}}$,

として定義される。

${\textstyle L^{\text{sym}}}$の要素は

$L_{i,j}^{\text{sym}}:={\begin{cases}1&{\mbox{if }}i=j{\mbox{ and }}\deg(v_{i})\neq 0\\-{\frac {1}{\sqrt {\deg(v_{i})\deg(v_{j})}}}&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}.\end{cases}}$

によって与えられる。

酔歩正規化ラプラシアン

酔歩正規化ラプラシアン行列は

$L^{\text{rw}}:=D^{-1}L=I-D^{-1}A$

として定義される。

${\textstyle L^{\text{rw}}}$の要素は

$L_{i,j}^{\text{rw}}:={\begin{cases}1&{\mbox{if }}i=j{\mbox{ and }}\deg(v_{i})\neq 0\\-{\frac {1}{\deg(v_{i})}}&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}.\end{cases}}$

によって与えられる。

一般化ラプラシアン

一般化ラプラシアンQは

${\begin{cases}Q_{i,j}<0&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is adjacent to }}v_{j}\\Q_{i,j}=0&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is not adjacent to }}v_{j}\\{\mbox{any number}}&{\mbox{otherwise}}.\end{cases}}$

として定義される。

普通のラプラシアンは一般化ラプラシアンであることが分かる。

例

以下はラベル付けされた無向グラフとそのラプラシアン行列の単純な例である。

ラベル付けされたグラフ	次数行列	隣接行列	ラプラシアン行列
	${\textstyle \left({\begin{array}{rrrrrr}2&0&0&0&0&0\\0&3&0&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrrrr}0&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{array}}\right)}$

性質

（無向）グラフGと固有値${\textstyle \lambda _{0}\leq \lambda _{1}\leq \cdots \leq \lambda _{n-1}}$を持つそのラプラシアン行列Lについて:

• Lは対称である。
• Lは半正定値である（すなわち全ての${\textstyle i}$について${\textstyle \lambda _{i}\geq 0}$）。これは接続行列の節で検証される。これは、ラプラシアンが対称であり、優対角であるという事実からも見ることができる。
• LはM-行列である（その非対角成分は非正であり、そのうえその固有値の実部は非負である）。
• Lの全ての行の和と列の和はゼロである。実際、和の計算において、頂点の次数には隣接する頂点ごとに「−1」が足される。
• その結果、${\textstyle \lambda _{0}=0}$となる。これは、ベクトル${\textstyle \mathbf {v} _{0}=(1,1,\dots ,1)}$が${\textstyle L\mathbf {v} _{0}=\mathbf {0} }$を満たすためである。これは、ラプラシアン行列が特異行列であることも暗示する。
• グラフ中の連結成分の数はラプラシアンの零空間の次元であり、0固有値の代数的多重度である。
• Lの最小の非ゼロ固有値はスペクトルギャップと呼ばれる。
• Lの2番目に小さな固有値（ゼロかもしれない）はGの代数的連結度（Fiedler値）であり、グラフの最疎カットを近似する。
• ラプラシアンは、関数${\textstyle f:V\to \mathbb {R} }$（${\textstyle V}$はGの頂点セット、${\textstyle n=|V|}$）のn次元ベクトル空間上の作用素である。
• Gがk正則である時、正規化ラプラシアンは${\textstyle {\mathcal {L}}={\tfrac {1}{k}}L=I-{\tfrac {1}{k}}A}$である（Aは隣接行列、Iは単位行列）。
• 複数の連結成分を持つグラフについて、Lは区分対角行列であり、それぞれの区分はそれぞれの成分についての（場合によると頂点を順序付けし直した後の）各ラプラシアン行列である（すなわちLは区分対角行列と置換相似である）。
• ラプラシアン行列Lの跡（トレース）は${\textstyle 2m}$（${\textstyle m}$は考慮されているグラフの辺の数）と等しい。

接続行列

$M_{ev}=\left\{{\begin{array}{rl}1,&{\text{if }}v=i\\-1,&{\text{if }}v=j\\0,&{\text{otherwise}}.\end{array}}\right.$

によって与えられる辺e（頂点iとjを連結している; i > j）と頂点vについて要素M_evを持つ${\textstyle |e|\times |v|}$有向接続行列Mを定義する。

次に、ラプラシアン行列Lは

$L=M^{\textsf {T}}M\,,$

を満たす（${\textstyle M^{\textsf {T}}}$はMの転置行列）。

ここで、単位ノルム固有値ベクトル${\textstyle \mathbf {v} _{i}}$および対応する固有値${\textstyle \lambda _{i}}$を使った${\textstyle L}$の固有値分解を考える。

${\begin{aligned}\lambda _{i}&=\mathbf {v} _{i}^{\textsf {T}}L\mathbf {v} _{i}\\&=\mathbf {v} _{i}^{\textsf {T}}M^{\textsf {T}}M\mathbf {v} _{i}\\&=\left(M\mathbf {v} _{i}\right)^{\textsf {T}}\left(M\mathbf {v} _{i}\right)\\\end{aligned}}$

${\textstyle \lambda _{i}}$はベクトル${\textstyle M\mathbf {v} _{i}}$とそれ自身の内積として書くことができるため、これは${\textstyle \lambda _{i}\geq 0}$であり、したがって${\textstyle L}$の固有値は全て非負であることを示す。

変形ラプラシアン

変形ラプラシアン（deformed laplacian）は通常以下のように定義される。

$\Delta (s)=I-sA+s^{2}(D-I)$

上式において、Iは単位行列、Aは隣接行列、Dは次数行列、sは（複素）数である。ここで留意すべきは、標準的なラプラシアンは単に${\textstyle \Delta (1)}$となることである。

対称正規化ラプラシアン

（対称）正規化ラプラシアンは以下のように定義される。

$L^{\text{sym}}:=D^{-{\frac {1}{2}}}LD^{-{\frac {1}{2}}}=I-D^{-{\frac {1}{2}}}AD^{-{\frac {1}{2}}}$

上式において、Lは（非正規化）ラプラシアン、Aは隣接行列、Dは次数行列である。次数行列Dは対角行列で正であるため、その逆数平方根${\textstyle D^{-{\frac {1}{2}}}}$は単にその対角成分がDの対角成分の正の平方根の逆数である対角行列となる。対称正規化ラプラシアンは対称行列である。

${\textstyle L^{\text{sym}}=SS^{*}}$が存在する。Sは、列が頂点によって添え字を付けられ、行がGの辺によって添え字が付けられた行列である。これらは、辺e = {u, v} に対応するそれぞれの行がuに対応する列において成分${\textstyle {\frac {1}{\sqrt {d_{u}}}}}$を、vに対応する列において成分${\textstyle -{\frac {1}{\sqrt {d_{v}}}}}$を、それ以外では0成分を持つことになるように索引付けされる（注: ${\textstyle S^{*}}$はSの転置行列を示す）。

正規化ラプラシアンの全ての固有値は実数かつ非負である。これは以下のように見ることができる。${\textstyle L^{\text{sym}}}$は対称であるため、その固有値は実数である。これらの固有値は全て非負である。固有値λを持つ${\textstyle L^{\text{sym}}}$の固有ベクトル ${\textstyle g}$を考え、${\textstyle g=D^{\frac {1}{2}}f}$を仮定する（gおよびfを頂点v上の実関数と見なすことができる）。すると、

$\lambda \ =\ {\frac {\langle g,L^{\text{sym}}g\rangle }{\langle g,g\rangle }}\ =\ {\frac {\left\langle g,D^{-{\frac {1}{2}}}LD^{-{\frac {1}{2}}}g\right\rangle }{\langle g,g\rangle }}\ =\ {\frac {\langle f,Lf\rangle }{\left\langle D^{\frac {1}{2}}f,D^{\frac {1}{2}}f\right\rangle }}\ =\ {\frac {\sum _{u\sim v}(f(u)-f(v))^{2}}{\sum _{v}f(v)^{2}d_{v}}}\ \geq \ 0,$

となる。ここでは内積${\textstyle \langle f,g\rangle =\sum _{v}f(v)g(v)}$（全ての頂点vにわたる和）を用い、${\textstyle \sum _{u\sim v}}$は隣接頂点 {u,v} の全ての非順序対にわたる和を示す。量${\textstyle \sum _{u,v}(f(u)-f(v))^{2}}$はfの「ディリクレ和」と呼ばれるが、式${\textstyle {\frac {\left\langle g,L^{\text{sym}}g\right\rangle }{\langle g,g\rangle }}}$はgのレイリー商と呼ばれる。

1をそれぞれの頂点上に値1を想定する関数とする。すると、${\textstyle D^{\frac {1}{2}}1}$は固有値0を持つ${\textstyle L^{\text{sym}}}$の固有関数である。

実際、正規化対称ラプラシアンの固有値は0 = μ₀ ≤ … ≤ μ_n−1 ≤ 2を満たす。これらの固有値（正規化ラプラシアンのスペクトルと呼ばれる）は、一般グラフに対するその他のグラフ不変量とよく関連する。

酔歩正規化ラプラシアン

酔歩（random walk）正規化ラプラシアンは

$L^{\text{rw}}:=D^{-1}L$

として定義される。Dは次数行列である。次数行列D対角行列であるため、その逆行列${\textstyle D^{-1}}$は単純に対角行列として定義され、これはDの対応する正の対角成分の逆数である対角成分を持つ。

孤立した頂点（次数が0）について、一般的な選択は対応する要素${\textstyle L_{i,i}^{\text{rw}}}$を0にすることでる。

この慣習によって、固有値0の多重度がグラフの連結した構成要素の数と等しくなるという良い性質がもたらされる。

${\textstyle L^{\text{rw}}}$の行列要素は以下の式で与えられる。

$L_{i,j}^{\text{rw}}:={\begin{cases}1&{\mbox{if}}\ i=j\ {\mbox{and}}\ \deg(v_{i})\neq 0\\-{\frac {1}{\deg(v_{i})}}&{\mbox{if}}\ i\neq j\ {\mbox{and}}\ v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}\end{cases}}$

酔歩正規化ラプラシアンの名称は、この行列が${\textstyle L^{\text{rw}}=I-P}$（${\textstyle P=D^{-1}A}$は単純にグラフ上の酔歩者〈ランダムウォーカー〉の遷移行列）という事実から来ている。例えば、${\textstyle e_{i}}$がi番目の標準基底ベクトルを示すものとする。すると、${\textstyle x=e_{i}P}$は頂点${\textstyle i}$から一歩進んだ後の酔歩者の位置の分布を示す確率ベクトルである; すなわち、 ${\textstyle x_{j}=\mathbb {P} \left(v_{i}\to v_{j}\right)}$。より一般的には、もしベクトル${\textstyle x}$がグラフの頂点上の酔歩者の位置の確率分布であるとすれば、${\textstyle x'=xP^{t}}$は${\textstyle t}$歩後の酔歩者の確率分布である。

$L^{\text{rw}}=I-D^{-{\frac {1}{2}}}\left(I-L^{\text{sym}}\right)D^{\frac {1}{2}}$

となることを確認することができる。

すなわち、${\textstyle L^{\text{rw}}}$は正規化ラプラシアン${\textstyle L^{\text{sym}}}$と類似している。この理由のため、${\textstyle L^{\text{rw}}}$がたとえ一般にエルミート行列でないとしても、実固有値を持つ。実際、その固有値は（エルミート行列である）${\textstyle L^{\text{sym}}}$のものと一致する。

グラフ

グラフ上の酔歩に関する余談として、単純無向グラフを考える。酔歩者が時間tに頂点iにいる確率を考え、酔歩者が時間t-1に頂点jにいた確率分布を仮定する（任意の頂点に結合したいかなる辺に沿った一歩について一様の見込みを仮定する）:

$p_{i}(t)=\sum _{j}{\frac {A_{ij}}{\deg \left(v_{j}\right)}}p_{j}(t-1),$

または行列-ベクトル記法で:

$p(t)=AD^{-1}p(t-1).$

（${\textstyle t\rightarrow \infty }$として設定される平衡は${\textstyle p=AD^{-1}p}$として定義される。）

この関係は

$D^{-{\frac {1}{2}}}p(t)=\left[D^{-{\frac {1}{2}}}AD^{-{\frac {1}{2}}}\right]D^{-{\frac {1}{2}}}p(t-1)$

と書き直すことができる。

${\textstyle A_{\text{reduced}}\equiv D^{-{\frac {1}{2}}}AD^{-{\frac {1}{2}}}}$は簡約隣接行列と呼ばれる対称行列である。したがって、この酔歩者の一歩は${\textstyle A_{\text{reduced}}}$の累乗を必要とする。${\textstyle A_{\text{reduced}}}$は対称行列であるため、これは単純な操作である。

離散ラプラス演算子としての解釈

ラプラシアン行列は、離散ラプラス演算子の特定の事例の行列表現として解釈することができる。このような解釈によって、例えば、ラプラシアン行列を無限の数の頂点と辺を持つグラフ（無限サイズのラプラシアン行列となる）の場合に一般化することが可能となる。

${\textstyle \phi }$がグラフにわたる熱分布を記述すると想定する（${\textstyle \phi _{i}}$は頂点${\textstyle i}$における熱である）。ニュートンの冷却の法則に従えば、節${\textstyle i}$と節${\textstyle j}$の間を移る熱は、もし節${\textstyle i}$と節${\textstyle j}$が連結されているならば、${\textstyle \phi _{i}-\phi _{j}}$に比例する（節が連結されていないならば、熱は移らない）。

すると、熱用量${\textstyle k}$について、

${\begin{aligned}{\frac {d\phi _{i}}{dt}}&=-k\sum _{j}A_{ij}\left(\phi _{i}-\phi _{j}\right)\\&=-k\left(\phi _{i}\sum _{j}A_{ij}-\sum _{j}A_{ij}\phi _{j}\right)\\&=-k\left(\phi _{i}\ \deg(v_{i})-\sum _{j}A_{ij}\phi _{j}\right)\\&=-k\sum _{j}\left(\delta _{ij}\ \deg(v_{i})-A_{ij}\right)\phi _{j}\\&=-k\sum _{j}\left(\ell _{ij}\right)\phi _{j}.\end{aligned}}$

行列-ベクトル記法では、

${\begin{aligned}{\frac {d\phi }{dt}}&=-k(D-A)\phi \\&=-kL\phi \end{aligned}}$

これから、

${\frac {d\phi }{dt}}+kL\phi =0$

が得られる。

この方程式が、行列 −Lがラプラス演算子${\textstyle \nabla ^{2}}$を置き換えている熱方程式と同じ形式であることに気付く。ゆえに、Lは「グラフラプラシアン」と呼ばれる。

この微分方程式の解を探すため、1階の行列微分方程式を解くための標準的な技法を適用する。すなわち、Lの固有ベクトル${\textstyle \mathbf {v} _{i}}$（${\textstyle L\mathbf {v} _{i}=\lambda _{i}\mathbf {v} _{i}}$）の線形結合として${\textstyle \phi }$を書く。時間に依存する${\textstyle \phi =\sum _{i}c_{i}\mathbf {v} _{i}}$。

元の式に代入する（ここで留意すべきは、Lが対称行列であるためにその単位ノルム固有ベクトル${\textstyle \mathbf {v} _{i}}$は直交であるという事実を用いる点である）:

${\begin{aligned}{\frac {d\left(\sum _{i}c_{i}\mathbf {v} _{i}\right)}{dt}}+kL\left(\sum _{i}c_{i}\mathbf {v} _{i}\right)&=0\\\sum _{i}\left[{\frac {dc_{i}}{dt}}\mathbf {v} _{i}+kc_{i}L\mathbf {v} _{i}\right]&=\\\sum _{i}\left[{\frac {dc_{i}}{dt}}\mathbf {v} _{i}+kc_{i}\lambda _{i}\mathbf {v} _{i}\right]&=\\{\frac {dc_{i}}{dt}}+k\lambda _{i}c_{i}&=0\\\end{aligned}}$

この解

$c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}$

である。

前掲のように、Lの固有値${\textstyle \lambda _{i}}$は非負であり、これは微分方程式の解が（指数関数的に減衰するか一定に留まるかのいずれかのみであるため）平衡に近づくことを示している。これは、${\textstyle \lambda _{i}}$と初期条件${\textstyle c_{i}(0)}$が与えられれば、いかなる時点における解も見つけることができることも示している。全体の初期条件${\textstyle \phi (0)}$の観点からそれぞれの${\textstyle i}$に対する${\textstyle c_{i}(0)}$を探すためには、単純に${\textstyle \phi (0)}$を単位ノルム固有ベクトル${\textstyle \mathbf {v} _{i}}$へと射影する。

$c_{i}(0)=\left\langle \phi (0),\mathbf {v} _{i}\right\rangle$

無向グラフの場合は、${\textstyle L}$が対称行列であるためこれはうまくいき、スペクトル定理によって、その固有ベクトルは全て直交する。そのため、${\textstyle L}$の固有ベクトルに対する射影は単純に、指数関数的に減衰し、互いに独立な一連の座標への初期条件の直交座標変換である。

平衡挙動

${\textstyle \lim _{t\to \infty }\phi (t)}$を理解するためには、残る項${\textstyle c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}}$は${\textstyle \lambda _{i}=0}$のもののみであることに留意すべきである。これは

$\lim _{t\to \infty }e^{-k\lambda _{i}t}=\left\{{\begin{array}{rlr}0&{\text{if}}&\lambda _{i}>0\\1&{\text{if}}&\lambda _{i}=0\end{array}}\right\}$

となるためである。

言い換えると、系の平衡状態は${\textstyle L}$の核によって完全に決定される。

なぜなら定義${\textstyle \sum _{j}L_{ij}=0}$によれば、全てが1のベクトル${\textstyle \mathbf {v} ^{1}}$は核内にある。また、グラフ中に${\textstyle k}$個の互いに素な連結成分が存在するならば、この全てが1のベクトルは1と0からなる${\textstyle k}$個の独立な${\textstyle \lambda =0}$固有ベクトルの和へと分割できる。それぞれの連結成分は連結成分中の要素では1を持つ固有ベクトルと、その他の場所では0を持つ固有ベクトルと対応している。

この結果は、${\textstyle N}$個の頂点を持つグラフについて任意の初期条件${\textstyle c(0)}$では、

$\lim _{t\to \infty }\phi (t)=\left\langle c(0),\mathbf {v^{1}} \right\rangle \mathbf {v^{1}}$

となる。上式において、

$\mathbf {v^{1}} ={\frac {1}{\sqrt {N}}}[1,1,...,1]$

である。

${\textstyle \phi }$の個々の要素${\textstyle \phi _{j}}$、すなわちグラフ中の個々の頂点${\textstyle j}$について、これを

$\lim _{t\to \infty }\phi _{j}(t)={\frac {1}{N}}\sum _{i=1}^{N}c_{i}(0)$

と書き直すことができる。

言い換えると、定常状態では、${\textstyle \phi }$の値はグラフの個々の頂点において同じ値に収束する。この値は全ての頂点の初期値の平均である。これは熱拡散方程式の解であるため、直感的に完全に筋が通っている。グラフ中で隣接する要素は、エネルギーが互いに連結した全ての要素にわたって均等に広がるまでエネルギーを交換することが予測される。

グリッド上の作用素の例

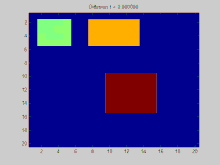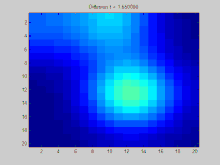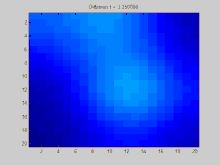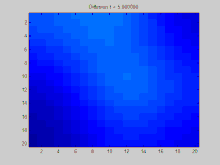
このGIFは、グラフラプラシアン法によって解かれたような拡散の進行を示している。グラフはグリッドにわたって構築され、グラフ中の個々のピクセルは隣接している8個のピクセルに連結している。次に、画像中の値はこれらの連結を介して隣接ピクセルへと滑らかに拡散する。この画像は、3つの点に強い値を持つ状態から始まり、この値はゆっくりと隣へ波及する。系全体は最終的に平衡に達すると同じ値に落ち着く。

本節では、グラフにわたって経時的に拡散する関数${\textstyle \phi }$の例を示す。この例中のグラフは2次元離散グリッド上に構築され、グリッド上の点は8個の隣接点と連結している。3つの初期点は正の値を持つと指定されているのに対し、グリッド中の残りの値は0である。経時的に、指数関数的減衰によってグリッド全体へとこれらの点上の値が均等に分布する。

このアニメーションを生成するために使われた完全なMATLABのソースコードを以下に示す。ソースコードは、初期条件の指定、これらの初期条件のラプラシアン行列の固有値への射影、これらの射影された初期条件の指数関数的減衰のシミュレーションの過程を示す。

N = 20;%The number of pixels along a dimension of the image
A = zeros(N, N);%The image
Adj = zeros(N*N, N*N);%The adjacency matrix

%Use 8 neighbors, and fill in the adjacency matrix
dx = [-1, 0, 1, -1, 1, -1, 0, 1];
dy = [-1, -1, -1, 0, 0, 1, 1, 1];
for x = 1:N
   for y = 1:N
       index = (x-1)*N + y;
       for ne = 1:length(dx)
           newx = x + dx(ne);
           newy = y + dy(ne);
           if newx > 0 && newx <= N && newy > 0 && newy <= N
               index2 = (newx-1)*N + newy;
               Adj(index, index2) = 1;
           end
       end
   end
end

%%%BELOW IS THE KEY CODE THAT COMPUTES THE SOLUTION TO THE DIFFERENTIAL
%%%EQUATION
Deg = diag(sum(Adj, 2));%Compute the degree matrix
L = Deg - Adj;%Compute the laplacian matrix in terms of the degree and adjacency matrices
[V, D] = eig(L);%Compute the eigenvalues/vectors of the laplacian matrix
D = diag(D);

%Initial condition (place a few large positive values around and
%make everything else zero)
C0 = zeros(N, N);
C0(2:5, 2:5) = 5;
C0(10:15, 10:15) = 10;
C0(2:5, 8:13) = 7;
C0 = C0(:);

C0V = V'*C0;%Transform the initial condition into the coordinate system 
%of the eigenvectors
for t = 0:0.05:5
   %Loop through times and decay each initial component
   Phi = C0V.*exp(-D*t);%Exponential decay for each component
   Phi = V*Phi;%Transform from eigenvector coordinate system to original coordinate system
   Phi = reshape(Phi, N, N);
   %Display the results and write to GIF file
   imagesc(Phi);
   caxis([0, 10]);
   title(sprintf('Diffusion t = %3f', t));
   frame = getframe(1);
   im = frame2im(frame);
   [imind, cm] = rgb2ind(im, 256);
   if t == 0
      imwrite(imind, cm, 'out.gif', 'gif', 'Loopcount', inf, 'DelayTime', 0.1); 
   else
      imwrite(imind, cm, 'out.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 0.1);
   end
end

負の連続的ラプラシアンに対する近似

グラフラプラシアン行列は、有限差分法によって得られた（半正定値）ラプラシアン作用素に対する近似の行列形式としてさらに見ることができる。この解釈では、グラフの全ての頂点はグリッド点として扱われる; 頂点の局所連結性はグリッド点における有限差分近似ステンシルを決定し、グリッドのサイズは常に全ての辺について1であり、いかなるグリッド点上にも制約はない。これは斉次なノイマン境界条件、すなわち自由境界の場合に相当する。

有向多重グラフ

ラプラシアン行列の類似物は、有向多重グラフに対しても定義することができる。この場合、ラプラシアン行列Lは

$L=D-A$

と定義される。上式においてDは頂点iの出次数と等しいD_i,iを持つ対角行列、Aはiからjへの辺の数（ループを含む）と等しいA_i,jを持つ行列である。

参考文献

• T. Sunada (2008). “Chapter 1. Analysis on combinatorial graphs. Discrete geometric analysis”. In P. Exner, J. P. Keating, P. Kuchment, T. Sunada, A. Teplyaev. 'Proceedings of Symposia in Pure Mathematics. 77. pp. 51–86. ISBN 978-0-8218-4471-7 
• B. Bollobás, Modern Graph Theory, Springer-Verlag (1998, corrected ed. 2013), ISBN 0-387-98488-7, Chapters II.3 (Vector Spaces and Matrices Associated with Graphs), VIII.2 (The Adjacency Matrix and the Laplacian), IX.2 (Electrical Networks and Random Walks).

関連項目

• 剛性行列
• 抵抗距離
• 推移速度行列