「皿ばね」の版間の差分
編集の要約なし |
|||
| (4人の利用者による、間の10版が非表示) | |||
| 1行目: | 1行目: | ||
[[Image:Belleville washer.jpg|thumb|275px|皿ばね]] |
[[Image:Belleville washer.jpg|thumb|275px|皿ばね]] |
||
'''皿ばね''' (さらばね) |
'''皿ばね''' (さらばね) は、中心に穴の開いた[[円盤|円盤状]]の板を円錐状にし、底のない[[皿|お皿]]のような形状にした[[ばね]]である<ref name="JISB0103">{{cite book |和書 |editor=日本工業標準調査会 |title=JIS B 0103 ばね用語 |year=2012 |page=8 }}</ref>。英語では、disc spring、coned disc spring、Belleville spring などと呼ぶ<ref name="JISB0103"/>。英語名の"Belleville"は、1865年に皿ばねの原理を発明したジュリアン・フランソワ・ベルビル (Julian Francois Belleville) に由来する{{Sfn|Oberg et al.|2012|p=350}}。 |
||
<ref name="JISB0103">{{cite book|和書 |
|||
|editor=日本工業標準調査会 |
|||
|title=JIS B 0103 ばね用語 |
|||
|year=2012 |
|||
|page=8 |
|||
}}</ref> |
|||
。自動車の[[クラッチ]]に使われるものは'''ダイヤフラムスプリング'''とも呼ばれる。 |
|||
英語では、disc spring、coned disc spring、Belleville springなどと呼び<ref name="JISB0103"/>、英語名の「ベリビル」は発明者のジュリアン・フランソワ・ベルビル (Julian Francois Belleville) に由来する |
|||
<ref>{{Citation | last = Shigley | first = Joseph Edward | last2 = Mischke | first2 = Charles R. | last3 = Brown | first3 = Thomas H. | title = Standard handbook of machine design | page = 640 | publisher = McGraw-Hill Professional | year = 2004 | edition = 3rd | url = http://books.google.com/books?id=Mafom8J9sqYC&pg=PT150 | isbn = 978-0-07-144164-3 | postscript =.}}</ref> 。 |
|||
== 特徴 == |
== 特徴 == |
||
円錐 |
皿ばねの円錐上側部分と下側部分に荷重を加え、高さを低くする方向にたわませることでばね作用が得られる。主に以下のような特徴を持つ。 |
||
*小さな取付スペースで大きな荷重を受けることができる |
*小さな取付スペースで大きな荷重を受けることができる{{Sfn|SCHNORR|2003|p=6}}。一般的なばねの種類である[[コイルばね]]が入らないような場所にも使えることがある{{Sfn|Oberg et al.|2012|p=350}}。 |
||
* |
*荷重とたわみの関係は[[非線形]]だが、形状の寸法比を変えることで累進的、逆進的、線形的などの様々なばね特性が得られる{{Sfn|SCHNORR|2003|p=6}}。一方、板厚などの製作誤差がばね特性に大きく影響しやすく、特性のばらつきが大きくなる{{Sfn|日本ばね学会(編)|2008|p=272}}。 |
||
* |
*皿ばね同士を組み合せることにより、さらに様々なばね特性が得られ、全体としてのばね高さも変えることができる{{Sfn|日本ばね学会(編)|2008|p=271}}{{Sfn|SCHNORR|2003|p=6}}。ただし、組み合わせて使用する場合はばねのずれを生じさせないために内側か外側にガイドが必要となる{{Sfn|日本ばね学会(編)|2008|p=272}}。 |
||
*摩擦によりばねに[[ヒステリシス]]が生じる。これにより減衰特性を得ることもできる |
*皿ばねがたわむと皿ばねは平らになる方向に変形する。そのため、たわみに伴って接触点が移動するため、摩擦によりばね特性に[[ヒステリシス]]が生じる{{Sfn|日本ばね学会(編)|2008|p=279}}。これにより減衰特性を得ることもできる{{Sfn|SCHNORR|2003|p=6}}。一方、摩擦によりガイドやばねの摩耗が生じたり、ヒステリシスを嫌う場合は潤滑材や表面研磨などを要する{{Sfn|日本ばね学会(編)|2008|p=279}}。 |
||
==使用例== |
|||
締結用の座金やクラッチの加圧バネなどに使用されている<ref name = "ばね_272"/>。 |
|||
[[File:Torque limiter with balls Make Ringspann.JPG|thumb|140px|[[トルクリミッター]]の例。ハの字状に積み重なった板が皿ばね。]] |
|||
皿ばねは、締結用の[[座金]]、[[クラッチ]]の加圧バネ、その他産業用機械など、広く使用されている{{Sfn|日本ばね学会(編)|2008|pp=272, 548}}。特に、自動車の[[クラッチ]]に使われるものは'''ダイヤフラムスプリング'''(diaphragm spring)とも呼ばれる{{Sfn|日本ばね学会(編)|2008|p=549}}。座金用として用いられる皿ばねは'''皿ばね座金'''と呼ばれる{{Sfn|ばね技術研究会(編)|2001|p=96}}。 |
|||
使用される皿ばねの大きさは、板厚は数十[[マイクロメートル|μm]]から数十[[ミリメートル|mm]]程度まで、外径は数mmから1[[メートル|m]]程度までと多岐にわたる{{Sfn|ばね技術研究会(編)|1998|p=30}}。皿ばねの材料には、用途に応じて様々な材料が使用される{{Sfn|Oberg et al.|2012|p=351}}。[[炭素鋼]]、[[合金鋼]]、[[ステンレス鋼]]、[[銅合金]]などが材料として利用されている{{Sfn|ばね技術研究会(編)|1998|p=31}}。 |
|||
== 計算式 == |
== 計算式 == |
||
| 24行目: | 19行目: | ||
[[File:Disc spring diagram.png|thumb|350px|皿ばねの寸法とアルメン・ラスロの式における応力、回転中心位置]] |
[[File:Disc spring diagram.png|thumb|350px|皿ばねの寸法とアルメン・ラスロの式における応力、回転中心位置]] |
||
[[File:Deformation of disc spring in Almen and Laszlo model.png|thumb|皿ばねのアルメン・ラスロの式における変形モデル]] |
[[File:Deformation of disc spring in Almen and Laszlo model.png|thumb|皿ばねのアルメン・ラスロの式における変形モデル]] |
||
皿ばねの[[荷重]] |
皿ばねの[[荷重]]と[[たわみ]](縮み)の関係式、および皿ばね四隅の[[応力]]の計算式としては、以下のアルメン・ラスロの近似式がある{{Sfn|日本ばね学会(編)|2008|p=272}}。皿ばねの外径を ''d<sub>e</sub>''、内径を ''d<sub>i</sub>''、板厚を ''t''、自由高さを ''h''<sub>0</sub> (≃ ''H''<sub>0</sub> − ''t'')とし、皿ばね材料の[[ヤング率]]を ''E''、[[ポアソン比]]を ''ν'' とする。係数を以下のように定義したとき、 |
||
:<math>\alpha = \frac{d_e}{d_i} \quad , \quad \beta = \frac{h_0}{t}</math> |
|||
{{Indent| |
|||
<math> |
:<math>C_1 = \frac{1}{\pi}\frac{\left( \frac{\alpha-1}{\alpha} \right)^2}{\frac{\alpha+1}{\alpha-1}-\frac{2}{\ln\alpha}} </math> |
||
:<math>C_2 = \frac{1}{\pi}\frac{6}{\ln\alpha}\left( \frac{\alpha-1}{\ln\alpha}-1\right) </math> |
|||
:<math>C_3 = \frac{3}{\pi}\frac{\alpha-1}{\ln\alpha} </math> |
|||
荷重 ''P'' とたわみ ''δ'' の関係: |
|||
<math>C_1 = \frac{1}{\pi}\frac{\left( \frac{\alpha-1}{\alpha} \right)^2}{\frac{\alpha+1}{\alpha-1}-\frac{2}{\ln\alpha}} </math> |
|||
:<math>P = \frac{4E}{1-\nu^2}\frac{t^3}{C_1 d_e^2} \delta \left[ \left( \beta-\frac{\delta}{t} \right) \left( \beta-\frac{\delta}{2t} \right)+1 \right]</math> |
|||
接線[[ばね定数]] ''k'' : |
|||
<math>C_2 = \frac{1}{\pi}\frac{6}{\ln\alpha}\left( \frac{\alpha-1}{\ln\alpha}-1\right) </math> |
|||
:<math>k = \frac{dP}{d\delta} = \frac{4E}{1-\nu^2}\frac{t^3}{C_1 d_e^2} \left[\beta^2 - 3\beta\frac{\delta}{t} +\frac{3}{2}\left(\frac{\delta}{t}\right)^2 +1 \right]</math> |
|||
各四隅の応力: |
|||
<math>C_3 = \frac{3}{\pi}\frac{\alpha-1}{\ln\alpha} </math> |
|||
:<math>\sigma_\mathrm{I} = \frac{4E}{1-\nu^2} \frac{t}{C_1 d_e^2} \delta \left[ -C_2 \left( \beta-\frac{\delta}{2t} \right) -C_3 \right]</math> |
|||
}} |
|||
:<math>\sigma_\mathrm{II} = \frac{4E}{1-\nu^2} \frac{t}{C_1 d_e^2} \delta \left[ -C_2 \left( \beta-\frac{\delta}{2t} \right) +C_3 \right]</math> |
|||
:<math>\sigma_\mathrm{III} = \frac{4E}{1-\nu^2} \frac{t}{\alpha C_1 d_e^2} \delta \left[ (2C_3-C_2) \left( \beta-\frac{\delta}{2t} \right) +C_3 \right]</math> |
|||
:<math>\sigma_\mathrm{IV} = \frac{4E}{1-\nu^2} \frac{t}{\alpha C_1 d_e^2} \delta \left[ (2C_3-C_2) \left( \beta-\frac{\delta}{2t} \right) -C_3 \right]</math> |
|||
円周長が変化しない回転中心の外径 ''d<sub>o</sub>'' : |
|||
荷重Pとたわみδの関係 |
|||
:<math> d_o = \frac{d_e-d_i}{\ln\alpha} </math> |
|||
{{Indent| |
|||
となる{{Sfn|日本ばね学会(編)|2008|p=273}}。ここで、ln は[[自然対数]]である。 |
|||
<math>P = \frac{4E}{1-\nu^2}\frac{h_0^3}{C_1 d_e^2} \delta \left[ \left( \beta-\frac{\delta}{h_0} \right) \left( \beta-\frac{\delta}{2h_0} \right)+1 \right]</math> |
|||
}} |
|||
上記の式は、1936年に[[ゼネラルモーターズ]]研究員のアルメン (J. O. Almen) とラスロ (A. László) により発表された{{Sfn|SCHNORR|2003|p=5}}<ref>{{Cite journal |author=J. O. Almen |author2=A. Laszlo |
|||
接線ばね定数k |
|||
|title=The Uniform-Section Disk Spring |journal=Transactions of the A.S.M.E. |volume=58 |year=1936 |publisher=ASME |pages=305-314 |url=http://www.shotpeener.com/library/pdf/1935000.pdf |format=pdf }}</ref>。式導出の仮定として、 |
|||
{{Indent| |
|||
*断面形状は変形せず、円周長が変化しない中立点を中心にして回転するようにして皿ばねが変形する。 |
|||
<math>k = \frac{dP}{d\delta} = \frac{4E}{1-\nu^2}\frac{h_0^3}{C_1 d_e^2} \left[\beta^2 - 3\beta\frac{\delta}{h_0} +\frac{3}{2}\left(\frac{\delta}{h}\right)^2 +1 \right]</math> |
|||
*回転角 ''φ'' は小さいとして、''φ'' の高次の項は無視する。 |
|||
}} |
|||
*荷重は円周上に一様に負荷され、変形は軸対称とする。 |
|||
以上を設定している{{Sfn|日本ばね学会(編)|2008|p=272}}。 |
|||
===荷重・たわみ特性曲線=== |
|||
各四隅の応力 |
|||
[[File:Disc spring load-deflection characteristic curve.svg|thumb|300px|アルメン・ラスロの式による皿ばねの荷重・たわみ特性曲線]] |
|||
{{Indent| |
|||
アルメン・ラスロの式で示されたように、荷重とたわみの関係は[[三次関数|3次曲線]]となっており、[[非線形]]な関係となっている{{Sfn|日本ばね学会(編)|2008|p=271}}。荷重・たわみ特性曲線の形状は、自由高さと板厚の比 ''h''<sub>0</sub> / ''t'' によって決定される{{Sfn|SCHNORR|2003|p=16}}。''h''<sub>0</sub> / ''t'' の値を小さくすれば、荷重とたわみの関係はほとんど[[線型性|線形]]となる{{Sfn|Oberg et al.|2012|p=361}}。''h''<sub>0</sub> / ''t'' = 1.4 になると、たわみ ''β'' が ''h''<sub>0</sub> に等しい付近で ''P'' 一定状態となる{{Sfn|ばね技術研究会(編)|1998|p=31}}。 |
|||
<math>\sigma_\mathrm{I} = \frac{4E}{1-\nu^2} \frac{h}{C_1 d_e^2} \delta \left[ -C_2 \left( \beta-\frac{\delta}{2h_0} \right) -C_3 \right]</math> |
|||
さらに ''h''<sub>0</sub> / ''t'' が大きくなると、曲線は極大値を持つようになり、極大値を過ぎたところでは負のばね定数を持つようになる{{Sfn|ばね技術研究会(編)|1998|p=31}}。このような荷重・たわみ曲線の場合は、荷重を増やしていくと、たわみが一気に増加する飛び移りが発生する{{Sfn|日本ばね学会(編)|2008|p=274}}。この飛び移りの特性を積極的に利用する使用方法もある{{Sfn|ばね技術研究会(編)|1998|p=30}}。一般的には、''h''<sub>0</sub> / ''t'' の値は0.4から1.3までの範囲内とすることが推奨されている{{Sfn|Oberg et al.|2012|p=361}}。 |
|||
<math>\sigma_\mathrm{II} = \frac{4E}{1-\nu^2} \frac{h}{C_1 d_e^2} \delta \left[ -C_2 \left( \beta-\frac{\delta}{2h_0} \right) +C_3 \right]</math> |
|||
実際の荷重・たわみ特性曲線は、アルメン・ラスロの式による曲線と差がある。''β'' / ''h''<sub>0</sub> が0.75を超えた辺りから、実際の曲線は計算式による曲線を大きく上回りだす{{Sfn|日本ばね学会(編)|2008|p=275}}。これは荷重支持点が変化する影響によるものである{{Sfn|日本ばね学会(編)|2008|p=275}}。このため、''β'' / ''h''<sub>0</sub> が 0.75あるいは0.8程度の範囲までのたわみで使用することが一般的には推奨されている{{Sfn|SCHNORR|2003|p=23}}。 |
|||
<math>\sigma_\mathrm{III} = \frac{4E}{1-\nu^2} \frac{h}{\alpha C_1 d_e^2} \delta \left[ (2C_3-C_2) \left( \beta-\frac{\delta}{2h_0} \right) +C_3 \right]</math> |
|||
<math>\sigma_\mathrm{IV} = \frac{4E}{1-\nu^2} \frac{h}{\alpha C_1 d_e^2} \delta \left[ (2C_3-C_2) \left( \beta-\frac{\delta}{2h_0} \right) -C_3 \right]</math> |
|||
}} |
|||
円周長が変化しない回転中心の外径d<sub>o</sub> |
|||
{{Indent| |
|||
<math> d_o = \frac{d_e-d_i}{\ln\alpha} </math> |
|||
}} |
|||
となる<ref name = "ばね_273"/>。 |
|||
上記の式は、1936年に[[ゼネラルモーターズ]]研究員のアルメン (J.O. Almen) とラスロA. László) により発表された<ref name = "Handbook_5"/><ref name = "Almen1936"/>。式導出の仮定として、 |
|||
*断面形状は変形せず、円周長が変化しない中立点を中心にして回転するようにして皿ばねが変形する。 |
|||
*回転角φは小さいとして、φの高次の項は無視する。 |
|||
*荷重は円周上に一様に負荷され、変形は軸対称とする。 |
|||
以上を設定している<ref name = "ばね_272"/>。 |
|||
===コーナーRの影響補正=== |
===コーナーRの影響補正=== |
||
アルメン・ラスロの式では皿ばね板の四隅にコーナーRはないものとして式が導出されている |
アルメン・ラスロの式では皿ばね板の四隅にコーナーRはないものとして式が導出されている{{Sfn|日本ばね学会(編)|2008|p=272}}。実際にコーナーRが付くと荷重支点の移動が発生し、荷重とたわみの関係でアルメン・ラスロの式による計算値と実測値の差が大きくなる。日本ばね工業会などでは次のように補正した荷重-たわみの関係式を導入している{{Sfn|日本ばね学会(編)|2008|p=278}}。 |
||
:<math>P = \frac{d_e-d_i}{(d_e-d_i)-3R} \frac{4E}{1-\nu^2}\frac{h_0^3}{C_1 d_e^2} \delta \left[ \left( \beta-\frac{\delta}{h_0} \right) \left( \beta-\frac{\delta}{2h_0} \right)+1 \right]</math> |
|||
{{Indent| |
|||
<math>P = \frac{d_e-d_i}{(d_e-d_i)-3R} \frac{4E}{1-\nu^2}\frac{h_0^3}{C_1 d_e^2} \delta \left[ \left( \beta-\frac{\delta}{h_0} \right) \left( \beta-\frac{\delta}{2h_0} \right)+1 \right]</math> |
|||
}} |
|||
ここで、<math>\frac{d_e-d_i}{(d_e-d_i)-3R}</math>が補正項である。 |
ここで、<math>\frac{d_e-d_i}{(d_e-d_i)-3R}</math>が補正項である。 |
||
== |
== 重ね合わせによる利用 == |
||
[[Image:Tellerfeder2.svg|thumb|200px|並列重ね3×直列組み合わせ2]] |
[[Image:Tellerfeder2.svg|thumb|200px|並列重ね3×直列組み合わせ2]] |
||
[[Image:Tellerfeder.svg|thumb|200px|直列組み合わせ6]] |
[[Image:Tellerfeder.svg|thumb|200px|直列組み合わせ6]] |
||
他のばねと同様、複数の皿ばねを使用することで直列あるいは並列のばね定数を得ることができる。[[フックの法則#ばねが複数の場合]]などを参照のこと |
他のばねと同様、複数の皿ばねを使用することで直列あるいは並列のばね定数を得ることができる。[[フックの法則#ばねが複数の場合]]などを参照のこと。 |
||
皿ばねを同じ向きに重ね合わさると並列ばねの効果を発揮する{{Sfn|日本ばね学会(編)|2008|p=275}}。この組み合せ方を'''並列重ね'''と呼ぶ{{Sfn|日本ばね学会(編)|2008|p=275}}。皿ばねを互い違いに重ね合わさると直列ばねの効果を発揮する{{Sfn|日本ばね学会(編)|2008|p=275}}。この組み合せ方を'''直列組合せ'''と呼ぶ{{Sfn|日本ばね学会(編)|2008|p=275}}。重ね合わせをしたときはバネ間での摩擦が増えるので、より大きく[[ヒステリシス]]が発生する{{Sfn|ばね技術研究会(編)|1998|p=31}}。また、重ね合わせて使用する場合は皿ばねが崩れないようにガイドが必要となり、ピン状のものを皿ばねに通すか、筒状のものに皿ばねを入れるかをする必要がある{{Sfn|ばね技術研究会(編)|2001|pp=88–89}}。 |
|||
皿ばねを ''n'' 枚並列重ねしたとき、総たわみ ''δ<sub>T</sub>'' は1枚のときと変わらない。一方で総荷重 ''P<sub>T</sub>'' は1枚のときの ''n'' 倍必要になる。''P'' と ''δ'' を1枚のときの荷重とたわみ、''L''<sub>0</sub> を重ね合わした皿ばねにおける無負荷時の総高さとする。これらを式で表せば |
|||
:<math>P_{T}=nP</math> |
|||
:<math>\delta_{T}=\delta</math> |
|||
:<math>L_0=H_0 + (n-1)t</math> |
|||
である{{Sfn|Oberg et al.|2012|p=353}}。 |
|||
一方、皿ばねを ''m'' 枚直列組合せしたときは、総荷重 ''P<sub>T</sub>'' は1枚のときと変わらないが、総たわみ ''δ<sub>T</sub>'' は1枚のときの ''m'' 倍になる。式は |
|||
:<math>P_{T}=P</math> |
|||
:<math>\delta_{T}=m \delta</math> |
|||
:<math>L_0=m H_0</math> |
|||
である{{Sfn|Oberg et al.|2012|p=352}}。 |
|||
皿ばねを ''n'' 枚並列重ね・''m'' 枚直列組合せしたときは、 |
|||
:<math>P_{T}=nP</math> |
|||
:<math>\delta_{T}=m \delta</math> |
|||
:<math>L_0=\left [ H_0 + (n-1)t \right ] m</math> |
|||
となる{{Sfn|ばね技術研究会(編)|2001|p=88}}。 |
|||
==スリット付き== |
|||
[[File:Ressort en coupelle.svg|thumb|140px|スリット付き皿ばねの例]] |
|||
たわみを大きくしたいような場合、スリットを付けた皿ばねの種類がある{{Sfn|ばね技術研究会(編)|2001|p=86}}。スリット付き皿ばねによって、応力あるいは荷重を低減させつつ、たわみを大きくすることができる{{Sfn|SCHNORR|2003|p=79}}{{Sfn|日本ばね学会(編)|2008|p=276}}。スリット付き皿ばねの荷重・たわみ特性は、スリット部の片持ち[[はり部材|はり]]とスリット無し部分の皿ばね本体の合成として考えることができる{{Sfn|ばね技術研究会(編)|2001|pp=86–87}}。より正確な特性評価や応力評価には[[有限要素法]]が必要とされる{{Sfn|日本ばね学会(編)|2008|pp=276–277}}。 |
|||
== 規格 == |
== 規格 == |
||
[[日本 |
[[日本産業規格]] |
||
*JIS B 2706 - 皿ばね |
*JIS B 2706 - 皿ばね<ref>{{cite jis|B|2706}}</ref> |
||
日本ばね工業会規格 |
|||
*JSMA SA 001 - 皿ばね |
|||
[[ドイツ工業規格]] |
[[ドイツ工業規格]] |
||
*DIN 2092 - |
*DIN 2092 - Tellerfedern - Berechnung |
||
*DIN 2093 - |
*DIN 2093 - Tellerfedern - Qualitätsanforderungen - Maße |
||
フランス規格 |
|||
* NF E25-104 - Rondelles ressorts coniques - Rondelles dynamiques (dites "belleville") |
|||
[[SAE規格]] |
|||
*SAE HS 1582 - Manual on Design and Manufacture of Coned Disk Springs (Belleville Springs) and Spring Washers |
|||
==脚注== |
==脚注== |
||
{{reflist|2 |
{{reflist|2}} |
||
refs= |
|||
<ref name = "ばね_271">[[#ばね|ばね p.271]]</ref> |
|||
<ref name = "ばね_272">[[#ばね|ばね p.272]]</ref> |
|||
<ref name = "ばね_273">[[#ばね|ばね p.273]]</ref> |
|||
<ref name = "ばね_275">[[#ばね|ばね p.275]]</ref> |
|||
<ref name = "ばね_278">[[#ばね|ばね p.278]]</ref> |
|||
<ref name = "ばね_279">[[#ばね|ばね p.279]]</ref> |
|||
<ref name = "Handbook_5">[[#Handbook|Handbook p.5]]</ref> |
|||
<ref name = "Handbook_6">[[#Handbook|Handbook p.6]]</ref> |
|||
<ref name = "Handbook_6">[[#Handbook|Handbook p.6]]</ref> |
|||
<ref name = "Almen1936">[[#Almen1936|Almen1936]]</ref> |
|||
}} |
|||
== |
==参照文献 == |
||
* {{Cite book |
* {{Cite book ja-jp |
||
|editor=日本ばね学会 |
|editor=日本ばね学会 |
||
|title=ばね |
|title=ばね |
||
| 110行目: | 114行目: | ||
|edition=第4版 |
|edition=第4版 |
||
|publisher=丸善出版 |
|publisher=丸善出版 |
||
|ref=ばね |
|||
|isbn =978-4-621-07965-2 |
|isbn =978-4-621-07965-2 |
||
|ref={{Sfnref|日本ばね学会(編)|2008}} |
|||
}} |
|||
*{{cite book ja-jp |
|||
|editor=ばね技術研究会 |
|||
|title=ばねの種類と用途例 |
|||
|series=ばね技術シリーズ |
|||
|publisher=日刊工業社 |
|||
|year=1998 |
|||
|edition=初版 |
|||
|isbn=4-526-04232-3 |
|||
|ref={{Sfnref|ばね技術研究会(編)|1998}} |
|||
}} |
|||
*{{cite book ja-jp |
|||
|editor=ばね技術研究会 |
|||
|title=ばねの設計と製造・信頼性 |
|||
|series=ばね技術シリーズ |
|||
|publisher=日刊工業社 |
|||
|year=2001 |
|||
|edition=初版 |
|||
|isbn=4-526-04705-8 |
|||
|ref={{Sfnref|ばね技術研究会(編)|2001}} |
|||
}} |
}} |
||
* {{Cite web |
* {{Cite web |
||
|url= http:// |
|url= http://www.industrialbearings.com.au/uploads/catalogs/schnorrhandbook_1343111178.pdf |
||
|title= Handbook for Disc Springs |
|title= Handbook for Disc Springs |
||
|format=PDF |
|format=PDF |
||
|publisher= |
|publisher= SCHNORR |
||
|accessdate= |
|accessdate=2016-08-10 |
||
|year=2003 |
|year=2003 |
||
|ref={{Sfnref|SCHNORR|2003}} |
|||
|ref=Handbook |
|||
}} |
}} |
||
* |
*{{cite book |
||
|title = Machinery's Handbook |
|||
|author=J.O. Almen |
|||
|author=Erik Oberg, Franklin Jones, Holbrook Horton, Henry Ryffel, Christopher McCauley |
|||
|author2=A. Laszlo |
|||
|publisher = Industrial Press |
|||
|title=The Uniform-Section Disk Spring |
|||
|year = 2012 |
|||
|journal=Transactions of the A.S.M.E. |
|||
|edition=29 |
|||
|volume=58 |
|||
|isbn=978-0-8311-2900-2 |
|||
|year=1936 |
|||
|ref={{Sfnref|Oberg et al.|2012}} |
|||
|publisher=[[アメリカ機械工学会|ASME]] |
|||
|pages=305-314 |
|||
|url=http://www.shotpeener.com/library/pdf/1935000.pdf |
|||
|format=pdf |
|||
|ref=Almen1936 |
|||
}} |
}} |
||
== |
==外部リンク== |
||
{{Commonscat |
{{Commonscat}} |
||
*[[ばね]] |
|||
*[[座金]] |
|||
{{DEFAULTSORT:さらはね}} |
{{DEFAULTSORT:さらはね}} |
||
2023年3月30日 (木) 22:51時点における最新版

皿ばね (さらばね) は、中心に穴の開いた円盤状の板を円錐状にし、底のないお皿のような形状にしたばねである[1]。英語では、disc spring、coned disc spring、Belleville spring などと呼ぶ[1]。英語名の"Belleville"は、1865年に皿ばねの原理を発明したジュリアン・フランソワ・ベルビル (Julian Francois Belleville) に由来する[2]。
特徴
[編集]皿ばねの円錐上側部分と下側部分に荷重を加え、高さを低くする方向にたわませることでばね作用が得られる。主に以下のような特徴を持つ。
- 小さな取付スペースで大きな荷重を受けることができる[3]。一般的なばねの種類であるコイルばねが入らないような場所にも使えることがある[2]。
- 荷重とたわみの関係は非線形だが、形状の寸法比を変えることで累進的、逆進的、線形的などの様々なばね特性が得られる[3]。一方、板厚などの製作誤差がばね特性に大きく影響しやすく、特性のばらつきが大きくなる[4]。
- 皿ばね同士を組み合せることにより、さらに様々なばね特性が得られ、全体としてのばね高さも変えることができる[5][3]。ただし、組み合わせて使用する場合はばねのずれを生じさせないために内側か外側にガイドが必要となる[4]。
- 皿ばねがたわむと皿ばねは平らになる方向に変形する。そのため、たわみに伴って接触点が移動するため、摩擦によりばね特性にヒステリシスが生じる[6]。これにより減衰特性を得ることもできる[3]。一方、摩擦によりガイドやばねの摩耗が生じたり、ヒステリシスを嫌う場合は潤滑材や表面研磨などを要する[6]。
使用例
[編集]
皿ばねは、締結用の座金、クラッチの加圧バネ、その他産業用機械など、広く使用されている[7]。特に、自動車のクラッチに使われるものはダイヤフラムスプリング(diaphragm spring)とも呼ばれる[8]。座金用として用いられる皿ばねは皿ばね座金と呼ばれる[9]。
使用される皿ばねの大きさは、板厚は数十μmから数十mm程度まで、外径は数mmから1m程度までと多岐にわたる[10]。皿ばねの材料には、用途に応じて様々な材料が使用される[11]。炭素鋼、合金鋼、ステンレス鋼、銅合金などが材料として利用されている[12]。
計算式
[編集]アルメン・ラスロの式
[編集]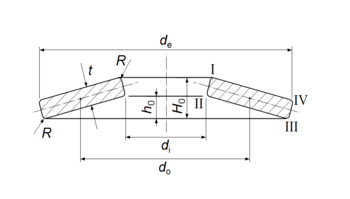

皿ばねの荷重とたわみ(縮み)の関係式、および皿ばね四隅の応力の計算式としては、以下のアルメン・ラスロの近似式がある[4]。皿ばねの外径を de、内径を di、板厚を t、自由高さを h0 (≃ H0 − t)とし、皿ばね材料のヤング率を E、ポアソン比を ν とする。係数を以下のように定義したとき、
荷重 P とたわみ δ の関係:
接線ばね定数 k :
各四隅の応力:
円周長が変化しない回転中心の外径 do :
上記の式は、1936年にゼネラルモーターズ研究員のアルメン (J. O. Almen) とラスロ (A. László) により発表された[14][15]。式導出の仮定として、
- 断面形状は変形せず、円周長が変化しない中立点を中心にして回転するようにして皿ばねが変形する。
- 回転角 φ は小さいとして、φ の高次の項は無視する。
- 荷重は円周上に一様に負荷され、変形は軸対称とする。
以上を設定している[4]。
荷重・たわみ特性曲線
[編集]
アルメン・ラスロの式で示されたように、荷重とたわみの関係は3次曲線となっており、非線形な関係となっている[5]。荷重・たわみ特性曲線の形状は、自由高さと板厚の比 h0 / t によって決定される[16]。h0 / t の値を小さくすれば、荷重とたわみの関係はほとんど線形となる[17]。h0 / t = 1.4 になると、たわみ β が h0 に等しい付近で P 一定状態となる[12]。
さらに h0 / t が大きくなると、曲線は極大値を持つようになり、極大値を過ぎたところでは負のばね定数を持つようになる[12]。このような荷重・たわみ曲線の場合は、荷重を増やしていくと、たわみが一気に増加する飛び移りが発生する[18]。この飛び移りの特性を積極的に利用する使用方法もある[10]。一般的には、h0 / t の値は0.4から1.3までの範囲内とすることが推奨されている[17]。
実際の荷重・たわみ特性曲線は、アルメン・ラスロの式による曲線と差がある。β / h0 が0.75を超えた辺りから、実際の曲線は計算式による曲線を大きく上回りだす[19]。これは荷重支持点が変化する影響によるものである[19]。このため、β / h0 が 0.75あるいは0.8程度の範囲までのたわみで使用することが一般的には推奨されている[20]。
コーナーRの影響補正
[編集]アルメン・ラスロの式では皿ばね板の四隅にコーナーRはないものとして式が導出されている[4]。実際にコーナーRが付くと荷重支点の移動が発生し、荷重とたわみの関係でアルメン・ラスロの式による計算値と実測値の差が大きくなる。日本ばね工業会などでは次のように補正した荷重-たわみの関係式を導入している[21]。
ここで、が補正項である。
重ね合わせによる利用
[編集]

他のばねと同様、複数の皿ばねを使用することで直列あるいは並列のばね定数を得ることができる。フックの法則#ばねが複数の場合などを参照のこと。
皿ばねを同じ向きに重ね合わさると並列ばねの効果を発揮する[19]。この組み合せ方を並列重ねと呼ぶ[19]。皿ばねを互い違いに重ね合わさると直列ばねの効果を発揮する[19]。この組み合せ方を直列組合せと呼ぶ[19]。重ね合わせをしたときはバネ間での摩擦が増えるので、より大きくヒステリシスが発生する[12]。また、重ね合わせて使用する場合は皿ばねが崩れないようにガイドが必要となり、ピン状のものを皿ばねに通すか、筒状のものに皿ばねを入れるかをする必要がある[22]。
皿ばねを n 枚並列重ねしたとき、総たわみ δT は1枚のときと変わらない。一方で総荷重 PT は1枚のときの n 倍必要になる。P と δ を1枚のときの荷重とたわみ、L0 を重ね合わした皿ばねにおける無負荷時の総高さとする。これらを式で表せば
である[23]。
一方、皿ばねを m 枚直列組合せしたときは、総荷重 PT は1枚のときと変わらないが、総たわみ δT は1枚のときの m 倍になる。式は
である[24]。
皿ばねを n 枚並列重ね・m 枚直列組合せしたときは、
となる[25]。
スリット付き
[編集]
たわみを大きくしたいような場合、スリットを付けた皿ばねの種類がある[26]。スリット付き皿ばねによって、応力あるいは荷重を低減させつつ、たわみを大きくすることができる[27][28]。スリット付き皿ばねの荷重・たわみ特性は、スリット部の片持ちはりとスリット無し部分の皿ばね本体の合成として考えることができる[29]。より正確な特性評価や応力評価には有限要素法が必要とされる[30]。
規格
[編集]- JIS B 2706 - 皿ばね[31]
日本ばね工業会規格
- JSMA SA 001 - 皿ばね
- DIN 2092 - Tellerfedern - Berechnung
- DIN 2093 - Tellerfedern - Qualitätsanforderungen - Maße
フランス規格
- NF E25-104 - Rondelles ressorts coniques - Rondelles dynamiques (dites "belleville")
- SAE HS 1582 - Manual on Design and Manufacture of Coned Disk Springs (Belleville Springs) and Spring Washers
脚注
[編集]- ^ a b 日本工業標準調査会 編『JIS B 0103 ばね用語』2012年、8頁。
- ^ a b Oberg et al. 2012, p. 350.
- ^ a b c d SCHNORR 2003, p. 6.
- ^ a b c d e 日本ばね学会(編) 2008, p. 272.
- ^ a b 日本ばね学会(編) 2008, p. 271.
- ^ a b 日本ばね学会(編) 2008, p. 279.
- ^ 日本ばね学会(編) 2008, pp. 272, 548.
- ^ 日本ばね学会(編) 2008, p. 549.
- ^ ばね技術研究会(編) 2001, p. 96.
- ^ a b ばね技術研究会(編) 1998, p. 30.
- ^ Oberg et al. 2012, p. 351.
- ^ a b c d ばね技術研究会(編) 1998, p. 31.
- ^ 日本ばね学会(編) 2008, p. 273.
- ^ SCHNORR 2003, p. 5.
- ^ J. O. Almen; A. Laszlo (1936). “The Uniform-Section Disk Spring” (pdf). Transactions of the A.S.M.E. (ASME) 58: 305-314.
- ^ SCHNORR 2003, p. 16.
- ^ a b Oberg et al. 2012, p. 361.
- ^ 日本ばね学会(編) 2008, p. 274.
- ^ a b c d e f 日本ばね学会(編) 2008, p. 275.
- ^ SCHNORR 2003, p. 23.
- ^ 日本ばね学会(編) 2008, p. 278.
- ^ ばね技術研究会(編) 2001, pp. 88–89.
- ^ Oberg et al. 2012, p. 353.
- ^ Oberg et al. 2012, p. 352.
- ^ ばね技術研究会(編) 2001, p. 88.
- ^ ばね技術研究会(編) 2001, p. 86.
- ^ SCHNORR 2003, p. 79.
- ^ 日本ばね学会(編) 2008, p. 276.
- ^ ばね技術研究会(編) 2001, pp. 86–87.
- ^ 日本ばね学会(編) 2008, pp. 276–277.
- ^ JIS B 2706(日本産業標準調査会、経済産業省)
参照文献
[編集]- 日本ばね学会(編)、2008、『ばね』第4版、丸善出版 ISBN 978-4-621-07965-2
- ばね技術研究会(編)、1998、『ばねの種類と用途例』初版、日刊工業社〈ばね技術シリーズ〉 ISBN 4-526-04232-3
- ばね技術研究会(編)、2001、『ばねの設計と製造・信頼性』初版、日刊工業社〈ばね技術シリーズ〉 ISBN 4-526-04705-8
- “Handbook for Disc Springs” (PDF). SCHNORR (2003年). 2016年8月10日閲覧。
- Erik Oberg, Franklin Jones, Holbrook Horton, Henry Ryffel, Christopher McCauley (2012). Machinery's Handbook (29 ed.). Industrial Press. ISBN 978-0-8311-2900-2





![{\displaystyle P={\frac {4E}{1-\nu ^{2}}}{\frac {t^{3}}{C_{1}d_{e}^{2}}}\delta \left[\left(\beta -{\frac {\delta }{t}}\right)\left(\beta -{\frac {\delta }{2t}}\right)+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40cfa852f164f4dfe534fc01228c615d86a9a388)
![{\displaystyle k={\frac {dP}{d\delta }}={\frac {4E}{1-\nu ^{2}}}{\frac {t^{3}}{C_{1}d_{e}^{2}}}\left[\beta ^{2}-3\beta {\frac {\delta }{t}}+{\frac {3}{2}}\left({\frac {\delta }{t}}\right)^{2}+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c675fc05258fa41bd5b718da232c530da002ced)
![{\displaystyle \sigma _{\mathrm {I} }={\frac {4E}{1-\nu ^{2}}}{\frac {t}{C_{1}d_{e}^{2}}}\delta \left[-C_{2}\left(\beta -{\frac {\delta }{2t}}\right)-C_{3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a29cbf9917871ce825a29cf0ccbb8c24da7220c)
![{\displaystyle \sigma _{\mathrm {II} }={\frac {4E}{1-\nu ^{2}}}{\frac {t}{C_{1}d_{e}^{2}}}\delta \left[-C_{2}\left(\beta -{\frac {\delta }{2t}}\right)+C_{3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/777487d1bc6c7f3166e424002e65e580beeb6d04)
![{\displaystyle \sigma _{\mathrm {III} }={\frac {4E}{1-\nu ^{2}}}{\frac {t}{\alpha C_{1}d_{e}^{2}}}\delta \left[(2C_{3}-C_{2})\left(\beta -{\frac {\delta }{2t}}\right)+C_{3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d0bcb474eaf8a16363d1d535c4fea2e6d12c077)
![{\displaystyle \sigma _{\mathrm {IV} }={\frac {4E}{1-\nu ^{2}}}{\frac {t}{\alpha C_{1}d_{e}^{2}}}\delta \left[(2C_{3}-C_{2})\left(\beta -{\frac {\delta }{2t}}\right)-C_{3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a5462005c28555a87f1f02781b940723a67185e)

![{\displaystyle P={\frac {d_{e}-d_{i}}{(d_{e}-d_{i})-3R}}{\frac {4E}{1-\nu ^{2}}}{\frac {h_{0}^{3}}{C_{1}d_{e}^{2}}}\delta \left[\left(\beta -{\frac {\delta }{h_{0}}}\right)\left(\beta -{\frac {\delta }{2h_{0}}}\right)+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24f3a8a37c87abd3fc9c0e433aef35473d5c6c0b)







![{\displaystyle L_{0}=\left[H_{0}+(n-1)t\right]m}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3fb498e15138d2afdf4261788d31c3583887f87)